-
设计了一种涂覆石墨烯的椭圆形电介质纳米线光波导. 采用分离变量法, 在椭圆柱坐标系中, 借助Mathieu函数, 得到了色散方程. 通过数值求解色散方程, 可以得到模式的有效折射率和场分布, 从而得到模式的传播长度. 研究了工作波长、结构参数以及石墨烯的费米能对模式特性的影响, 并给出了前五个模式的品质因数. 计算表明, 当波长从4.3
${\text{μ}}{\rm{m}}$ 增加到8.8${\text{μ}}{\rm{m}}$ , 这5个模式的有效折射率的实部减小, 基模和一阶模的传播长度增大, 二阶模的传播长度先增大后减小. 当改变纳米线结构参数半长轴和半短轴时, 对基模和一阶模的模式特性影响较小, 对二阶模的模式特性影响较大. 当石墨烯的费米能从0.45 eV增加到0.72 eV时, 有效折射率的实部减小, 传播长度可以达到2${\text{μ}}{\rm{m}}$ 左右. 分离变量法得到的结果与有限元方法得到的结果完全一致. 本文工作可以为基于涂覆石墨烯的电介质纳米线的光波导的设计、制作和应用提供理论基础.In this paper, an elliptical dielectric graphene-coated nanowire optical waveguide is designed. In the elliptical cylinder coordinate system, the dispersion equation is obtained by using the separation variable method with the Mathieu functions. The effective refractive indexes and the field distributions are obtained from the dispersion equation by using the numerical method, then the propagation lengths are obtained. The influence of the operating wavelength, structure parameters and the Fermi energy of graphene on the mode characteristics are investigated. What is more, the figure of merit of the first five modes are calculated too. The influence of the operating wavelength and the graphene Fermi energy on the mode characteristics of circular nanowires and that of elliptical nanowires are compared. The results show that as the operating wavelength increases from 4.3${\text{μ}}{\rm{m}}$ to 8.8${\text{μ}}{\rm{m}}$ , the real part of the effective refractive index decreases monotonically, the propagation lengths of the fundamental mode and the 1st order modes increase, and the 2nd order modes first increase and then decrease. When changing the elliptical nanowire structure parameters—the length of semi-major axis and semi-minor axis, there are slight influence on the mode characteristics of the fundamental mode and the 1st order modes, but greater influence on those of the 2nd order modes. As the Fermi energy of graphene increases from 0.45 eV to 0.72 eV, in the first five modes, the real part of the effective refractive index decreases, the propagation lengths of the fundamental mode and the 1st order modes increase, the propagation lengths of the 2nd order modes decrease. In addition, the propagation length approaches to 2${\text{μ}}{\rm{m}}$ approximately. When the semi-minor axis b = 100 nm and ${E_{\rm F}} \;{\rm{ = 0}}{\rm{.5}}\;{\rm{eV}}$ , the curves of the circular nanowire (a = 100 nm) and the elliptical nanowire (a = 140 nm), the real part of the effective refractive index and propagation length with the operating wavelength and the Fermi energy of graphene are compared. Then, the advantages of elliptical nanowire over the circular nanowire are verified. The results of the separation variable method are in good agreement with the results of the finite element method. This work can provide a theoretical basis for the design, fabrication and application of optical waveguides based on graphene-coated elliptical dielectric nanowires.-
Keywords:
- graphene /
- nanowires /
- waveguides /
- separation variable method
[1] Gao Y X, Ren G B, Zhu B F, Liu H Q, Lian Y D, Jian S S 2014 Opt. Express 22 24322
Google Scholar
[2] Novoselov K S, Geim A K, Morozov S V, Jiang D, Zhang Y, Grigorieva I V, Dubonos S V, Firsov A A 2004 Science 306 666
Google Scholar
[3] Novoselov K S, Geim A K, Morozov S V, Jiang D, Katsnelson M I, Grigorieva I V, Dubonos S V, Firsov A A 2005 Nature 438 197
Google Scholar
[4] Ju L, Geng B S, Horng J, Girit C, Martin M, Hao Z, Bechtel H A, Liang X G, Zettl A, Shen Y R, Wang F 2011 Nature Nanotechnol. 6 630
Google Scholar
[5] Wang J C, Song C, Hang J, Hu Z D, Zhang F 2017 Opt. Express 25 23880
Google Scholar
[6] Gao Y X, Ren G B, Zhu B F, Liu H Q, Wang J, Jian S S 2014 Opt. Lett. 39 5909
Google Scholar
[7] Jablan M, Buljan M, Soljačić M 2009 Phys. Rev. B 80 245435
Google Scholar
[8] Christensen J, Manjavacas A, Thongrattanasiri S, Koppens F H, de García Abajo F J 2012 ACS Nano 6 431
Google Scholar
[9] Liu P H, Zhang X Z, Ma Z H, Cai W, Wang L, Xu J J 2013 Opt. Express 21 32431
[10] Xing R, Jian S S 2016 IEEE Photonics Technol. Lett. 28 2649
Google Scholar
[11] Zhou X T, Zhang T, Chen L, Hong W, Li X 2014 J. Lightwave Technol. 32 3597
[12] Liu Y, Zhong R B, Ding H, Liu S G 2017 Eur. Phys. J. D 71 83
Google Scholar
[13] He X Q, Ning T G, Lu S H, Zheng J J, Li J, Li R J, Pei L 2018 Opt. Express 26 10109
Google Scholar
[14] Xing R, Jian S S 2017 IEEE Photonics Technol. Lett. 29 1643
Google Scholar
[15] Liu J P, Zhai X, Xie F, Wang L L, Xia S X, Liu H J, Luo X, Shang X J 2017 J. Lightwave Technol. 35 1971
Google Scholar
[16] Xing R, Jian S S 2017 IEEE Photonics Technol. Lett. 29 967
Google Scholar
[17] Zhu B F, Ren G B, Yang Y, Gao Y X 2015 Plasmonics 10 839
Google Scholar
[18] 彭艳玲, 薛文瑞, 卫壮志, 李昌勇 2018 光学学报 38 0223002
Peng Y L, Xue W R, Wei Z Z, Li C Y 2018 Acta Opt. Sin. 38 0223002
[19] 彭艳玲, 薛文瑞, 卫壮志, 李昌勇 2018 67 038102
Google Scholar
Peng Y L, Xue W R, Wei Z Z, Li C Y 2018 Acta Phys. Sin. 67 038102
Google Scholar
[20] Xing R, Jian S S 2016 IEEE Photonics Techol. Lett. 28 2779
Google Scholar
[21] 卫壮志, 薛文瑞, 程鑫, 李昌勇 2018 67 108101
Google Scholar
Wei Z Z, Xue W R, Cheng X, Li C Y 2018 Acta Phys. Sin. 67 108101
Google Scholar
[22] Hossein M B, Alexander B Y 2015 J. Phys. Condens. Matter 27 185304
Google Scholar
[23] 陈卫东, 刘丰 2009 电子学报 37 1624
Google Scholar
Chen W D, Liu F 2009 Acta Elec. Sin. 37 1624
Google Scholar
[24] Zhao J J, Tang M, Oh K H, Feng Z H, Zhao K, Liao R L, Fu S N, Shum P P, Liu D M 2017 Photon. Res. 8 261
[25] Nejad R M, Tavakoli F, Wang L X, Guan X, Larochelle S, Rusch L A 2018 J. Lightwave Technol. 36 3794
Google Scholar
[26] Lee M S, Park B G, Cho I H, Lee J H 2012 IEEE Electron Device Lett. 33 1613
Google Scholar
[27] de Abajo F J G 2010 Rev. Mod. Phys. 82 209
Google Scholar
[28] 翟利, 薛文瑞, 杨荣草, 韩丽萍 2015 光学学报 35 1123002
Zhai L, Xue W R, Yang R C, Han L P 2015 Acta Opt. Sin. 35 1123002
[29] Nikitin A Y, Guinea F, García-Vidal F J, Martín-Moreno L 2011 Phys.Rev. B 84 195446
Google Scholar
[30] Yeh C 1962 J. Appl. Phys. 33 3235
Google Scholar
[31] D Erricolo, G Carluccio 2013 ACM Trans. Math. Soft. 40 8
[32] He S L, Zhang X Z, He Y R 2013 Opt. Express 21 30664
Google Scholar
[33] Ye L F, Sui K H, Liu Y H, Zhang M, Liu Q H 2018 Opt. Express 26 15935
Google Scholar
[34] Ye S, Wang Z X, Sun C R, Dong C B, Wei B Z, Wu B L, Jian S S 2018 Opt. Express 26 23854
Google Scholar
[35] Chen M, Sheng P C, Sun W, Cai J J 2016 Opt.Commun. 376 41
Google Scholar
-
图 1 涂覆石墨烯的椭圆形电介质纳米线光波导的横截面示意图
Fig. 1. Cross section of the optical waveguide based on graphene-coated elliptical dielectric nanowire.
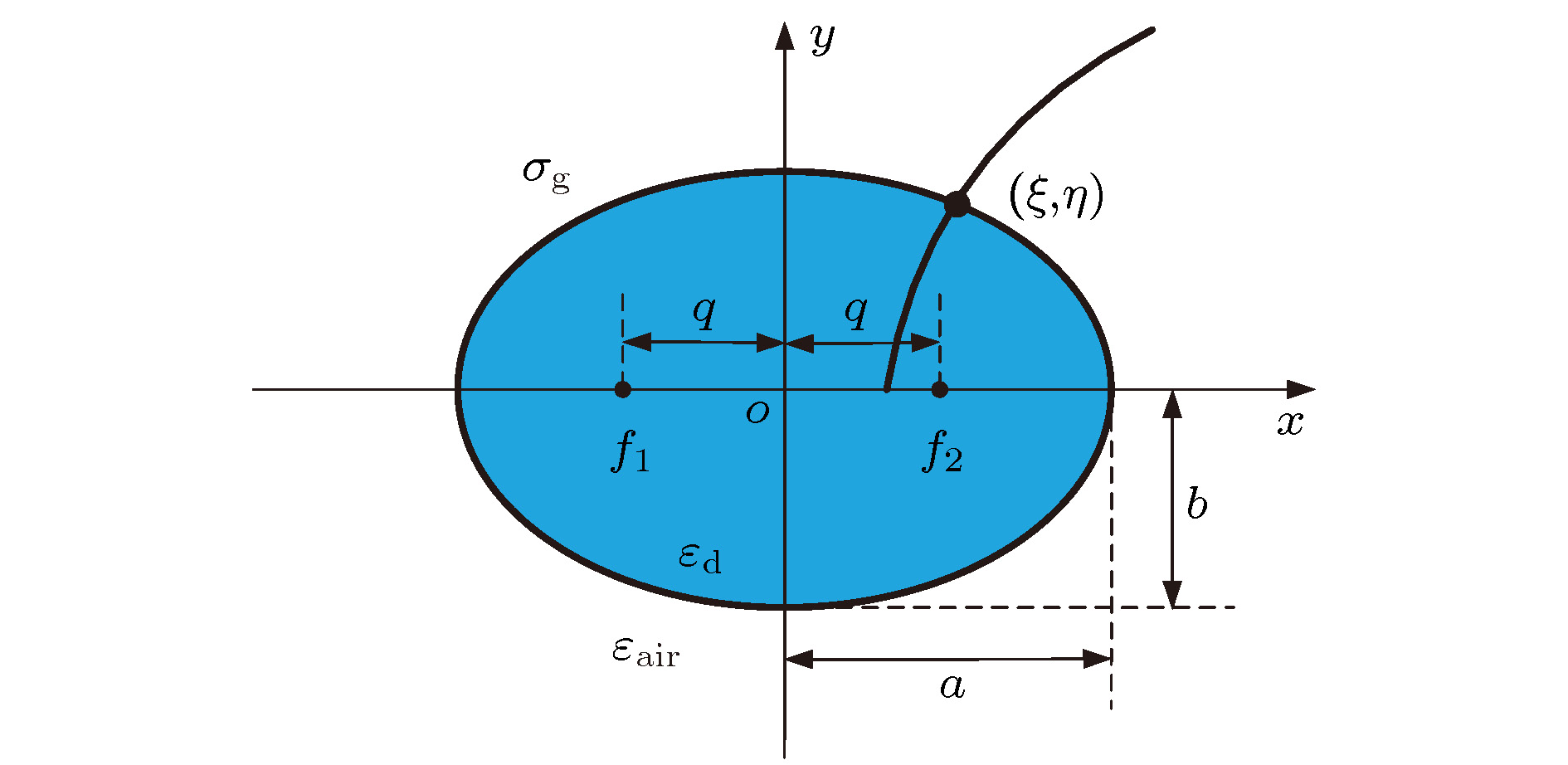
图 2 在a = 110 nm, b = 80 nm,
${E_{\rm{F}}}= 0{\rm{.5\; eV}}$ 和$\lambda = 7\;{\text{μ}}{\rm{m}}$ 的情况下, 前五个模式对应的z方向电场分量${E_z}$ (a)—(e)与电场强度$\left| E \right|$ 分布图(f)—(j)Fig. 2. The z direction electric field component
${E_z}$ (a)—(e)and electric field intensity$\left| E \right|$ (f)—(j) corresponding to the first 5 modes with a = 110 nm, b = 80 nm,${E_{\rm{F}}} = 0{\rm{.5\; eV}}$ and$\lambda = 7\;{\text{μ}}{\rm{m}}$ .
图 3 在a = 110 nm, b = 80 nm和
${E_{\rm{F}}} = 0{\rm{.5\; eV}}$ 的情况下, 有效折射率实部(a), 传播长度(b)和品质因数(c)与波长的关系Fig. 3. Dependence of the real part of the effective refractive index (a), propagation length (b) and FOM (c) on the wavelength with a = 110 nm, b = 80 nm and
${E_{\rm{F}}} = 0{\rm{.5\; eV}}$ .
图 4 在a = 110 nm, b = 80 nm和
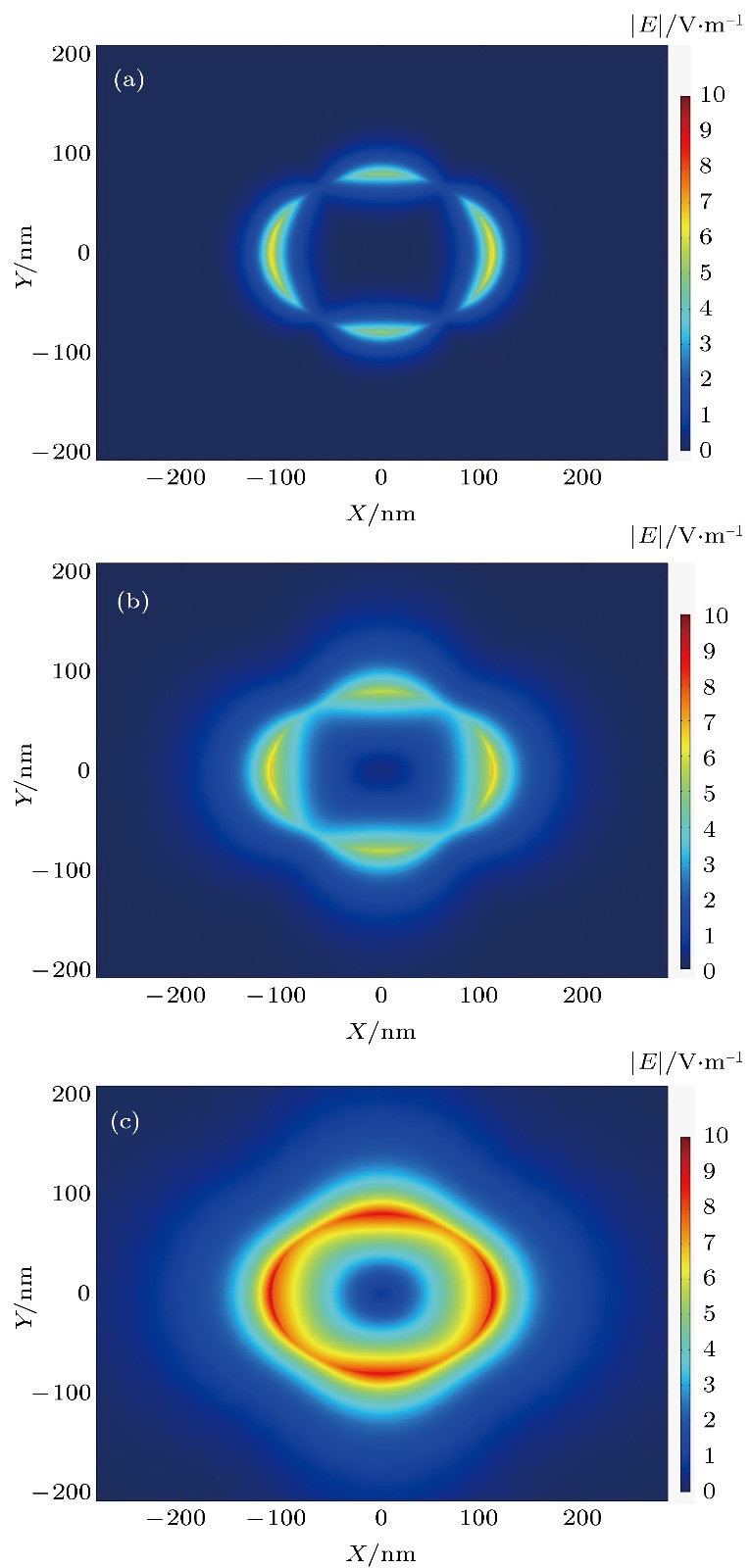
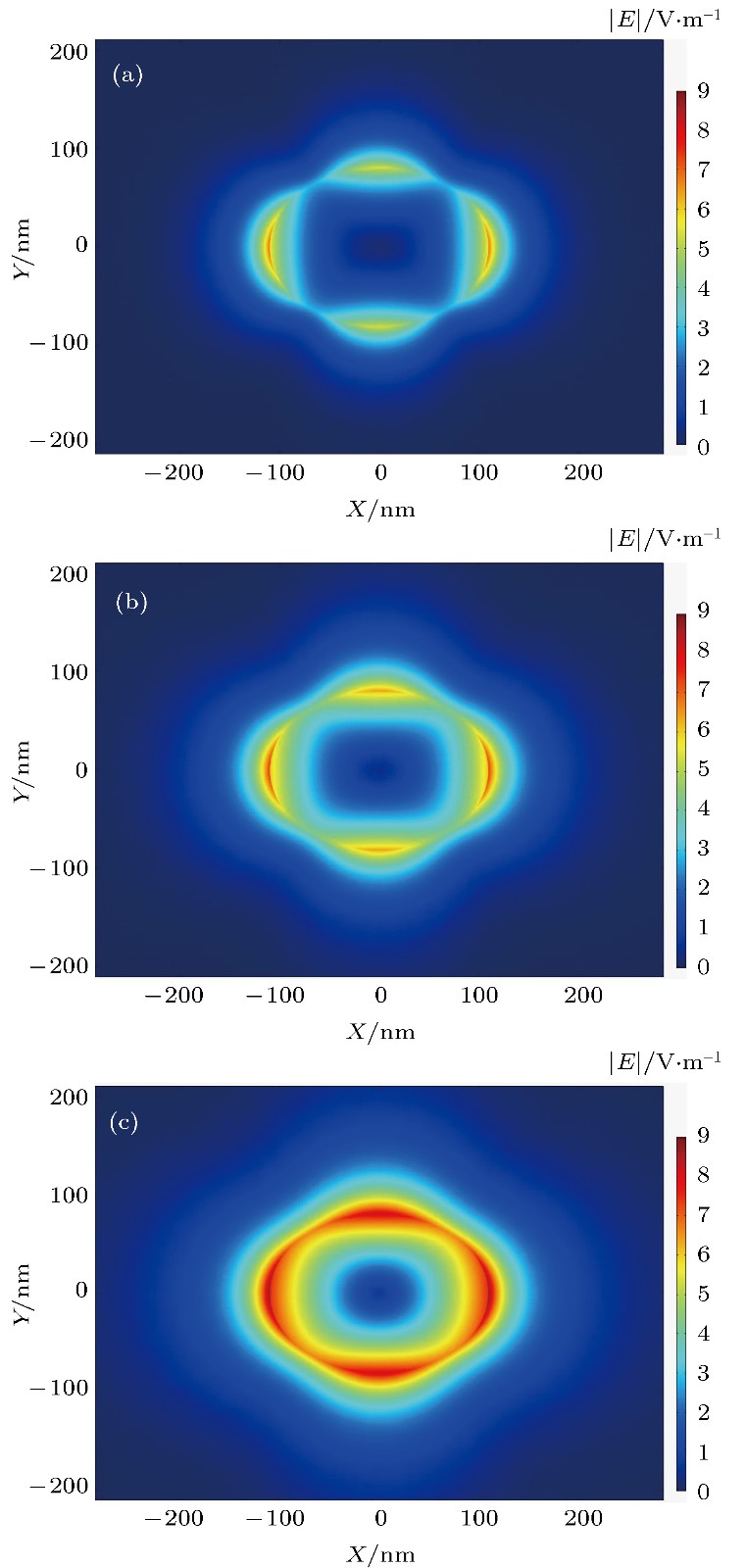
${E_{\rm{F}}} = 0{\rm{.5 \;eV}}$ 的情况下, 不同波长时Mode 5的电场强度$\left| E \right|$ 分布图 (a)$\lambda = 5{\rm{.0}}\;{\text{μ}}{\rm{m}}$ ; (b)$\lambda = {\rm{7}}{\rm{.5}}\;{\text{μ}}{\rm{m}}$ ; (c)$\lambda = {\rm{8}}{\rm{.5}}\;{\text{μ}}{\rm{m}}$ Fig. 4. The distribution of the electric field intensity
$\left| E \right|$ of the Mode 5 with different wavelength when a = 110 nm, b = 80 nm and${E_{\rm{F}}} = 0{\rm{.5 \;eV}}$ : (a)$\lambda = 5{\rm{.0}}\;{\text{μ}}{\rm{m}}$ ; (b)$\lambda = {\rm{7}}{\rm{.5}}\;{\text{μ}}{\rm{m}}$ ; (c)$\lambda = {\rm{8}}{\rm{.5}}\;{\text{μ}}{\rm{m}}$ .
图 5 b = 90 nm,
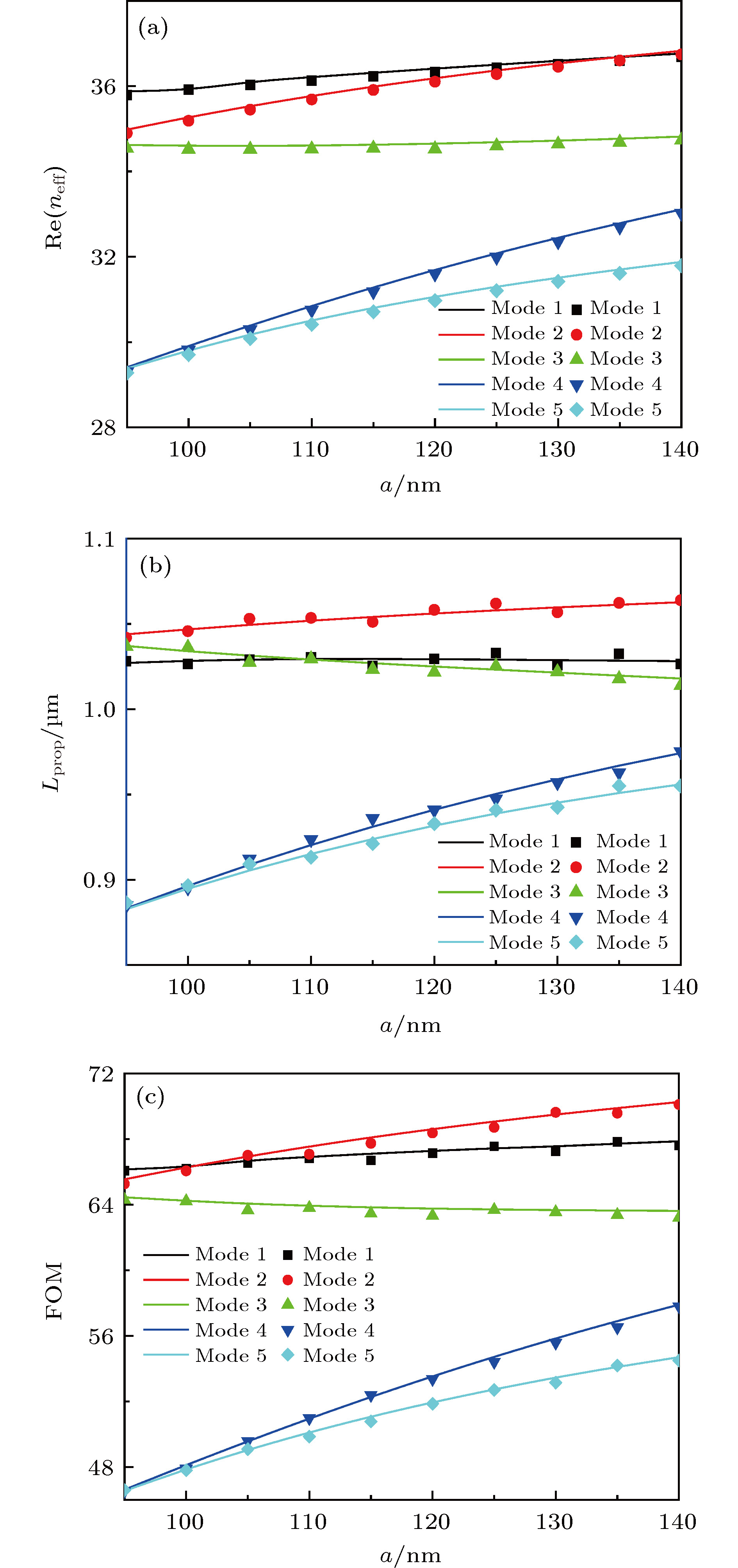
${E_{\rm{F}}} = 0{\rm{.5 \;eV}}$ 和$\lambda = 7\;{\text{μ}}{\rm{m}}$ 的情况下, 有效折射率实部(a), 传播长度(b)和品质因数(c)与半长轴a的关系Fig. 5. The real part of the effective refractive index (a), propagation length (b) and FOM (c) as a function of semi-major axis when b = 90 nm,
${E_{\rm{F}}}= 0{\rm{.5 \;eV}}$ and$\lambda = 7\;{\text{μ}}{\rm{m}}$ .
图 6 在b = 80 nm,
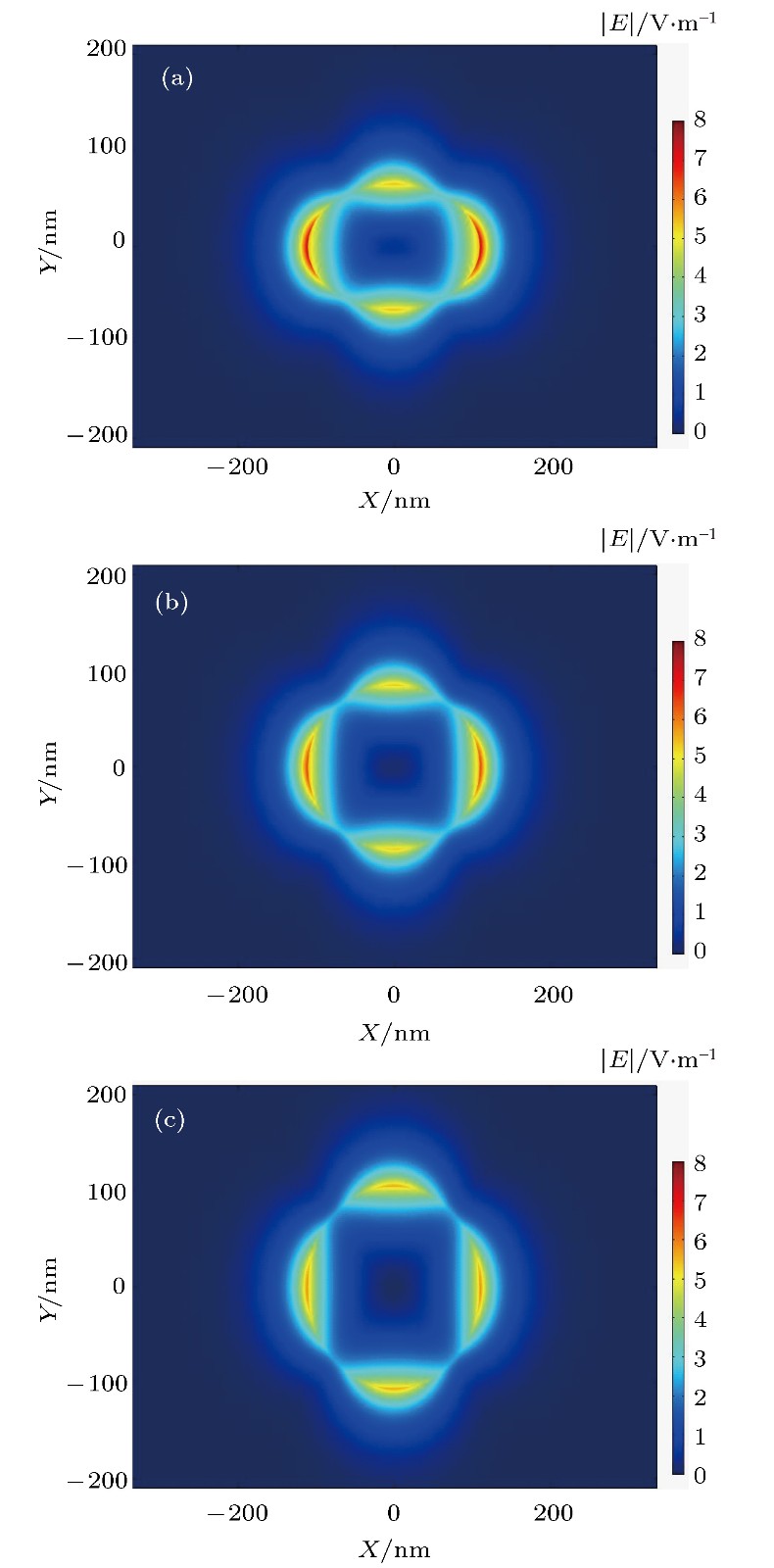
${E_{\rm{F}}} = 0{\rm{.5 \;eV}}$ 和$\lambda = 7\;{\text{μ}}{\rm{m}}$ 的情况下, 半长轴长度取不同值时Mode 5的电场强度$\left| E \right|$ 分布图 (a) a = 100 nm; (b) a = 120 nm; (c) a = 140 nmFig. 6. The distribution of the electric field intensity
$\left| E \right|$ of the Mode 5 with different length of semi-major axis when b = 80 nm,${E_{\rm{F}}}= 0{\rm{.5 \;eV}}$ and$\lambda = 7\;{\text{μ}}{\rm{m}}$ : (a) a = 100 nm; (b) a = 120 nm; (c) a = 140 nm.
图 7 当a = 110 nm,
${E_{\rm{F}}} = 0{\rm{.5 \;eV}}$ 和$\lambda = 7\;{\text{μ}}{\rm{m}}$ 时, 有效折射率实部(a), 传播长度(b)和品质因数(c)与半短轴b的关系Fig. 7. The real part of the effective refractive index (a), propagation length (b) and FOM (c) as a function of semi-minor axis when a = 110 nm,
${E_{\rm{F}}} = 0{\rm{.5 \;eV}}$ and${\rm{7}}\;{\text{μ}}{\rm{m}}$ .
图 8 在a = 110 nm,
${E_{\rm{F}}} = 0{\rm{.5 \;eV}}$ 和$\lambda = 7\;{\text{μ}}{\rm{m}}$ 的情况下, 半短轴长度取不同值时Mode 5的电场强度$\left| E \right|$ 分布图 (a) b = 65 nm; (b) b = 85 nm; (c) b = 105 nm.Fig. 8. The distribution of the electric field intensity
$\left| E \right|$ of the Mode 5 with different length of semi-minor axis when a = 110 nm,${E_{\rm F}}= 0{\rm{.5 \;eV}}$ and$\lambda = 7\;{\text{μ}}{\rm{m}}$ : (a) b = 65 nm; (b) b = 85 nm; (c) b = 105 nm.
图 9 当a = 110 nm, b = 80 nm和
$\lambda = 7\;{\text{μ}}{\rm{m}}$ 时, 有效折射率实部(a), 传播长度(b)和品质因数(c)与费米能的关系Fig. 9. The real part of the effective refractive index (a), propagation length (b) and FOM (c) as a function of Fermi energy when a = 110 nm, b = 80 nm and
$\lambda = 7\;{\text{μ}}{\rm{m}}$ .
图 10 在a = 110 nm, b = 80 nm和
$\lambda = 7\;{\text{μ}}{\rm{m}}$ 的情况下, 费米能取不同值时Mode 5的电场强度$\left| E \right|$ 分布图 (a)${E_{\rm{F}}} = 0{\rm{.5 \;eV}}$ ; (b)${E_{\rm F}} = 0{\rm{.63 \;eV}}$ ; (c)${E_{\rm F}} = 0{\rm{.72 \;eV}}$ Fig. 10. The distribution of the electric field intensity
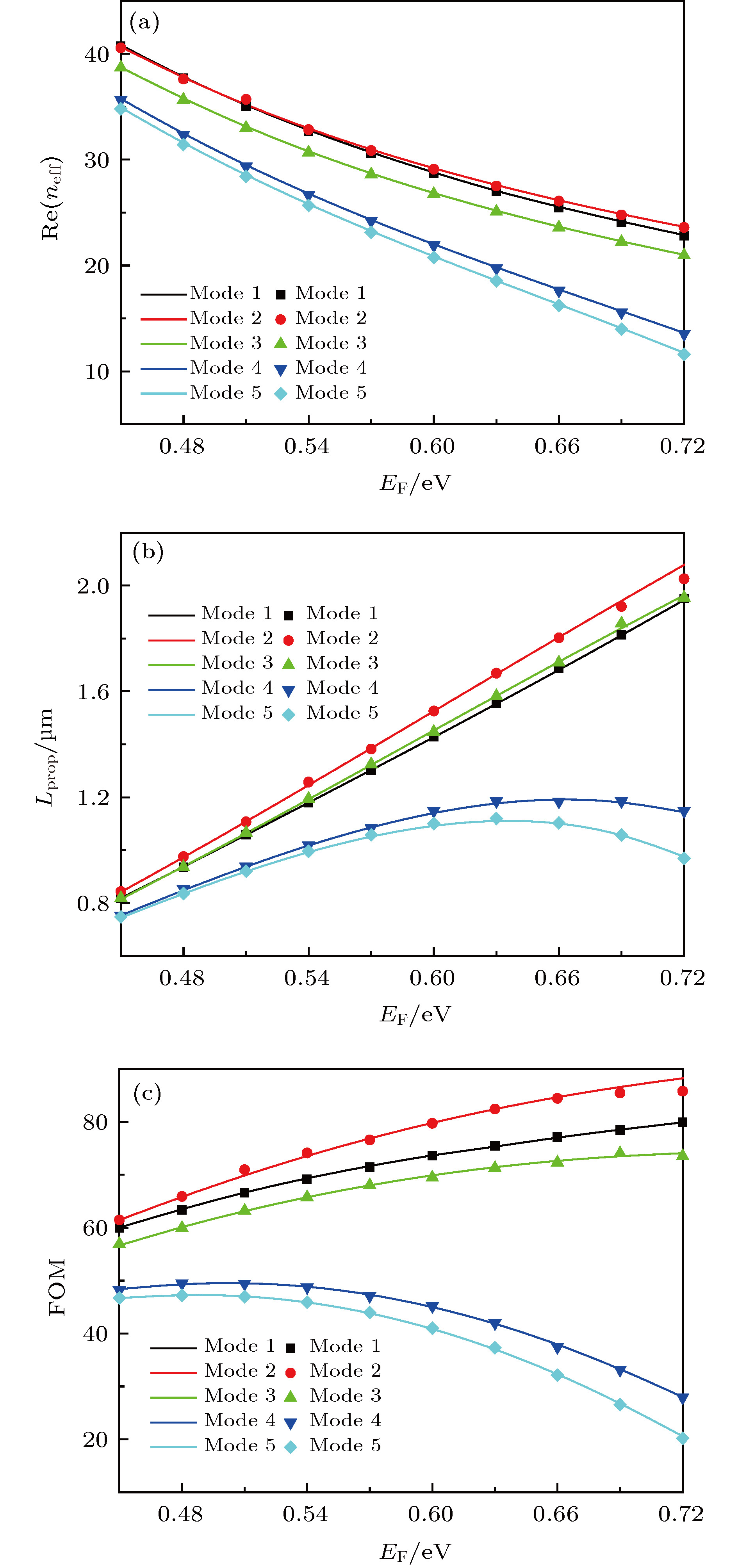
$\left| E \right|$ of the Mode 5 with different values of Fermi energy when a = 110 nm, b = 80 nm,$\lambda = 7\;{\text{μ}}{\rm{m}}$ : (a)${E_{\rm F}} = 0{\rm{.5 \;eV}}$ ; (b)${E_{\rm F}} = {\rm{0}}{\rm{.63 \;eV}}$ ; (c)${E_{\rm F}} = {\rm{0}}{\rm{.72 \;eV}}$ .
图 11 在
${E_{\rm{F}}}= 0{\rm{.5 \;eV}}$ 和b = 100 nm的条件下, 当a = 100和140 nm时, Mode 5 的有效折射率实部(a)和传播长度(b)随波长变化的曲线图Fig. 11. When a = 100 and 140 nm, the real part of the effective refractive index (a) , propagation length (b) as a function of wavelength at
${E_{\rm{F}}} = 0{\rm{.5 \;eV}}$ and b = 100 nm.
图 12 在b = 100 nm和
$\lambda = 7\;{\text{μ}}{\rm{m}}$ 的条件下, 当a = 100和140 nm时, Mode 5 的有效折射率实部(a)和传播长度(b)随石墨烯费米能变化的曲线图Fig. 12. When a = 100 and 140 nm, the real part of the effective refractive index (a), propagation length (b) as a function of graphene Fermi energy at b = 100 nm and
$\lambda = 7\;{\text{μ}}{\rm{m}}$ . -
[1] Gao Y X, Ren G B, Zhu B F, Liu H Q, Lian Y D, Jian S S 2014 Opt. Express 22 24322
Google Scholar
[2] Novoselov K S, Geim A K, Morozov S V, Jiang D, Zhang Y, Grigorieva I V, Dubonos S V, Firsov A A 2004 Science 306 666
Google Scholar
[3] Novoselov K S, Geim A K, Morozov S V, Jiang D, Katsnelson M I, Grigorieva I V, Dubonos S V, Firsov A A 2005 Nature 438 197
Google Scholar
[4] Ju L, Geng B S, Horng J, Girit C, Martin M, Hao Z, Bechtel H A, Liang X G, Zettl A, Shen Y R, Wang F 2011 Nature Nanotechnol. 6 630
Google Scholar
[5] Wang J C, Song C, Hang J, Hu Z D, Zhang F 2017 Opt. Express 25 23880
Google Scholar
[6] Gao Y X, Ren G B, Zhu B F, Liu H Q, Wang J, Jian S S 2014 Opt. Lett. 39 5909
Google Scholar
[7] Jablan M, Buljan M, Soljačić M 2009 Phys. Rev. B 80 245435
Google Scholar
[8] Christensen J, Manjavacas A, Thongrattanasiri S, Koppens F H, de García Abajo F J 2012 ACS Nano 6 431
Google Scholar
[9] Liu P H, Zhang X Z, Ma Z H, Cai W, Wang L, Xu J J 2013 Opt. Express 21 32431
[10] Xing R, Jian S S 2016 IEEE Photonics Technol. Lett. 28 2649
Google Scholar
[11] Zhou X T, Zhang T, Chen L, Hong W, Li X 2014 J. Lightwave Technol. 32 3597
[12] Liu Y, Zhong R B, Ding H, Liu S G 2017 Eur. Phys. J. D 71 83
Google Scholar
[13] He X Q, Ning T G, Lu S H, Zheng J J, Li J, Li R J, Pei L 2018 Opt. Express 26 10109
Google Scholar
[14] Xing R, Jian S S 2017 IEEE Photonics Technol. Lett. 29 1643
Google Scholar
[15] Liu J P, Zhai X, Xie F, Wang L L, Xia S X, Liu H J, Luo X, Shang X J 2017 J. Lightwave Technol. 35 1971
Google Scholar
[16] Xing R, Jian S S 2017 IEEE Photonics Technol. Lett. 29 967
Google Scholar
[17] Zhu B F, Ren G B, Yang Y, Gao Y X 2015 Plasmonics 10 839
Google Scholar
[18] 彭艳玲, 薛文瑞, 卫壮志, 李昌勇 2018 光学学报 38 0223002
Peng Y L, Xue W R, Wei Z Z, Li C Y 2018 Acta Opt. Sin. 38 0223002
[19] 彭艳玲, 薛文瑞, 卫壮志, 李昌勇 2018 67 038102
Google Scholar
Peng Y L, Xue W R, Wei Z Z, Li C Y 2018 Acta Phys. Sin. 67 038102
Google Scholar
[20] Xing R, Jian S S 2016 IEEE Photonics Techol. Lett. 28 2779
Google Scholar
[21] 卫壮志, 薛文瑞, 程鑫, 李昌勇 2018 67 108101
Google Scholar
Wei Z Z, Xue W R, Cheng X, Li C Y 2018 Acta Phys. Sin. 67 108101
Google Scholar
[22] Hossein M B, Alexander B Y 2015 J. Phys. Condens. Matter 27 185304
Google Scholar
[23] 陈卫东, 刘丰 2009 电子学报 37 1624
Google Scholar
Chen W D, Liu F 2009 Acta Elec. Sin. 37 1624
Google Scholar
[24] Zhao J J, Tang M, Oh K H, Feng Z H, Zhao K, Liao R L, Fu S N, Shum P P, Liu D M 2017 Photon. Res. 8 261
[25] Nejad R M, Tavakoli F, Wang L X, Guan X, Larochelle S, Rusch L A 2018 J. Lightwave Technol. 36 3794
Google Scholar
[26] Lee M S, Park B G, Cho I H, Lee J H 2012 IEEE Electron Device Lett. 33 1613
Google Scholar
[27] de Abajo F J G 2010 Rev. Mod. Phys. 82 209
Google Scholar
[28] 翟利, 薛文瑞, 杨荣草, 韩丽萍 2015 光学学报 35 1123002
Zhai L, Xue W R, Yang R C, Han L P 2015 Acta Opt. Sin. 35 1123002
[29] Nikitin A Y, Guinea F, García-Vidal F J, Martín-Moreno L 2011 Phys.Rev. B 84 195446
Google Scholar
[30] Yeh C 1962 J. Appl. Phys. 33 3235
Google Scholar
[31] D Erricolo, G Carluccio 2013 ACM Trans. Math. Soft. 40 8
[32] He S L, Zhang X Z, He Y R 2013 Opt. Express 21 30664
Google Scholar
[33] Ye L F, Sui K H, Liu Y H, Zhang M, Liu Q H 2018 Opt. Express 26 15935
Google Scholar
[34] Ye S, Wang Z X, Sun C R, Dong C B, Wei B Z, Wu B L, Jian S S 2018 Opt. Express 26 23854
Google Scholar
[35] Chen M, Sheng P C, Sun W, Cai J J 2016 Opt.Commun. 376 41
Google Scholar
下载:
计量
- 文章访问数: 7801
- PDF下载量: 57
- 被引次数: 0
