-
研究了束缚在梯子形光晶格中的中性原子与高精度腔耦合的系统, 发现由超辐射引起的准周期调制可以导致迁移率边和重返局域化现象的出现. 在平均场近似下, 超辐射现象可以引起两种不同频率的准周期调制, 它们可以由腔场和泵浦场有效调节. 在本文的观测范围内, 当高频调制强度小于某一临界值时, 系统随着低频调制强度的增加经历一次局域转变. 通过数值求解分形维度、密度分布、平均参与率、平均逆参与率以及标度分析, 证明了局域转变历经的临界相区存在迁移率边; 当高频调制强度大于临界值时, 随着低频调制强度的增强, 系统依次经历完全扩展相-临界相-完全局域相-临界相-完全局域相, 这是一个典型的重返局域化现象. 最后给出了局域化相图. 该研究结果为超辐射相变和重返局域化现象的研究建立了联系, 也为重返局域化的研究搭建了新的平台.We study a Bose-Einstein condensate trapped by a ladder lattice in a high-fitness cavity. The ladder lattice is loaded in the
$x\text-y$ plane and the cavity is along the x direction. A pump laser shines on atoms from the z direction. Under the mean-field approximation, we consider the emergence of the quasi-periodic potentials induced by superradiance in the ladder lattice, which is described by$\hat{H}_{\text{MF}}=\hat{H}_{\text{Lad}}+\hat{V}_{\text{eff}}$ with the effective potential$\hat{V}_{\text{eff}}(\alpha)={\displaystyle \sum\nolimits_{i = 1}^{N}}\displaystyle \sum\nolimits_{\sigma = 1,2}\left[\lambda_{\rm{D}}\cos({2\pi\beta i})+U_{\rm{D}}\cos^{2}({2\pi\beta i})\right]\hat{c}^{†}_{i,\sigma}\hat{c}_{i,\sigma}$ . We find that the quasi-periodic potential can induce the reentrant localization transition and the regime with mobility edges. In the smaller$U_{\rm{D}}$ case, the system exhibits a localization transition. The transition is associated with an intermediate regime with mobility edges. When$U_{\rm{D}}$ goes beyond a critical value$U_{\rm{D}}^{(\rm c)}$ , with the increase of$\lambda_{\rm{D}}$ , the system undergoes a reentrant localization transition. This indicates that after the first transition, some of the localized eigenstates change back to the extended ones for a range of$\lambda_{\rm{D}}$ . For a larger$\lambda_{\rm{D}}$ , the system experiences the second localization transition, then all states become localized again. Finally, the local phase diagram of the system is also discussed. This work builds a bridge between the reentrant localization and the superradiance, and it provides a new perspective for the reentrant localization.-
Keywords:
- superradiance /
- disorder /
- mobility edges /
- localization
[1] Marklund M, Shukla P K 2006 Rev. Mod. Phys. 78 591
Google Scholar
[2] Chin C, Grimm R, Julienne P, Tiesinga E 2010 Rev. Mod. Phys. 82 1225
Google Scholar
[3] Mekhov I B, Maschler C, Ritsch H 2007 Nat. Phys. 3 319
Google Scholar
[4] Ritsch H, Domokos P, Brennecke F, Esslinger T 2013 Rev. Mod. Phys. 85 553
Google Scholar
[5] Baumann K, Guerlin C, Brennecke F, Esslinger T 2010 Nature 464 1301
Google Scholar
[6] Maschler C, Mekhov I B, Ritsch H 2008 Eur. Phys. J. D 46 545
Google Scholar
[7] Klinder J, Keβler H, Bakhtiari M R, Thorwart M, Hemmerich A 2015 Phys. Rev. Lett. 115 230403
Google Scholar
[8] Landig R, Hruby L, Dogra N, Landini M, Mottl R, Donner T, Esslinger T 2016 Nature 532 476
Google Scholar
[9] Zheng W, Cooper N R 2018 Phys. Rev. A 97 021601(R
Google Scholar
[10] Zhou L, Pu H, Zhang K Y, Zhao X D, Zhang W P 2011 Phys. Rev. A 84 043606
Google Scholar
[11] Habibian H, Winter A, Paganelli S, Rieger H, Morigi G 2013 Phys. Rev. Lett. 110 075304
Google Scholar
[12] Anderson P W 1958 Phys. Rev. 109 1492
Google Scholar
[13] Aubry S, André G 1980 Ann. Isr.: Phys. Soc. 3 18
[14] Roati G, D’Errico C, Fallani L, Fattori M, Fort C, Zaccanti M, Modugno G, Modugno M, Inguscio M 2008 Nature 453 895
Google Scholar
[15] Sarma S D, Kobayashi A, Prange R E 1986 Phys. Rev. Lett. 56 1280
Google Scholar
[16] Sarma S D, Song H, Xie X C 1988 Phys. Rev. Lett. 61 2144
Google Scholar
[17] Biddle J, Sarma S D 2010 Phys. Rev. Lett. 104 070601
Google Scholar
[18] Ganeshan S, Pixley J H, Sarma S D 2015 Phys. Rev. Lett. 114 146601
Google Scholar
[19] Lanini Y, Bromberg Y, Christodoulides D N, Silberberg Y 2010 Phys. Rev. Lett. 105 163905
Google Scholar
[20] Xu Z H, Xia X, Chen S 2021 arXiv: 2109.02072 v1[cond-mat.dis-nn]
[21] Wang Y C, Xia X, Wang Y J, Zheng Z H, Liu X J 2021 Phys. Rev. B 103 174205
Google Scholar
[22] 徐志浩, 皇甫宏丽, 张云波 2019 68 087201
Google Scholar
Xu Z H, Huangfu H L, Zhang Y B 2019 Acta Phys. Sin. 68 087201
Google Scholar
[23] Xu Z H, Xia X, Chen S 2022 Sci. China-Phys. Mech. Astron. 65 227211
Google Scholar
[24] Roy S, Mishra T, Tanatar B, Basu S 2021 Phys. Rev. Lett 126 106803
Google Scholar
[25] Jiang X P, Qiao Y, Cao J P 2021 Chin. Phys. B 30 097202
Google Scholar
[26] Padhan A, Giri M K, Mondal S, Mishra T 2021 arXiv: 2109.09621 v1 [cond-mat.quant-gas]
[27] Zhuang W F, Geng B, Lou H G, Guo G C, Gong M 2021 Phys. Rev. A 104 053308
Google Scholar
[28] Keeling J, Bhaseen M J, Simons B D 2014 Phys. Rev. Lett 112 143002
Google Scholar
[29] Piazza F, Strack P 2014 Phys. Rev. Lett. 112 143003
Google Scholar
[30] Chen Y, Yu Z H, Zhai H 2014 Phys. Rev. Lett. 112 143004
Google Scholar
[31] Chen Y, Zhai H, Yu Z H 2015 Phys. Rev. A 91 021602(R
Google Scholar
[32] Chen Y, Yu Z H, Zhai H 2016 Phys. Rev. A 93 041601(R
Google Scholar
[33] Cai M L, Liu Z D, Zhao W D, Wu Y K, Mei Q X, Jiang Y, He L, Zhang X, Zhou Z C, Duan L M 2021 Nat. Commun. 12 1126
Google Scholar
[34] Xu Z H, Chen S 2021 Phys. Rev. A 103 043325
Google Scholar
-
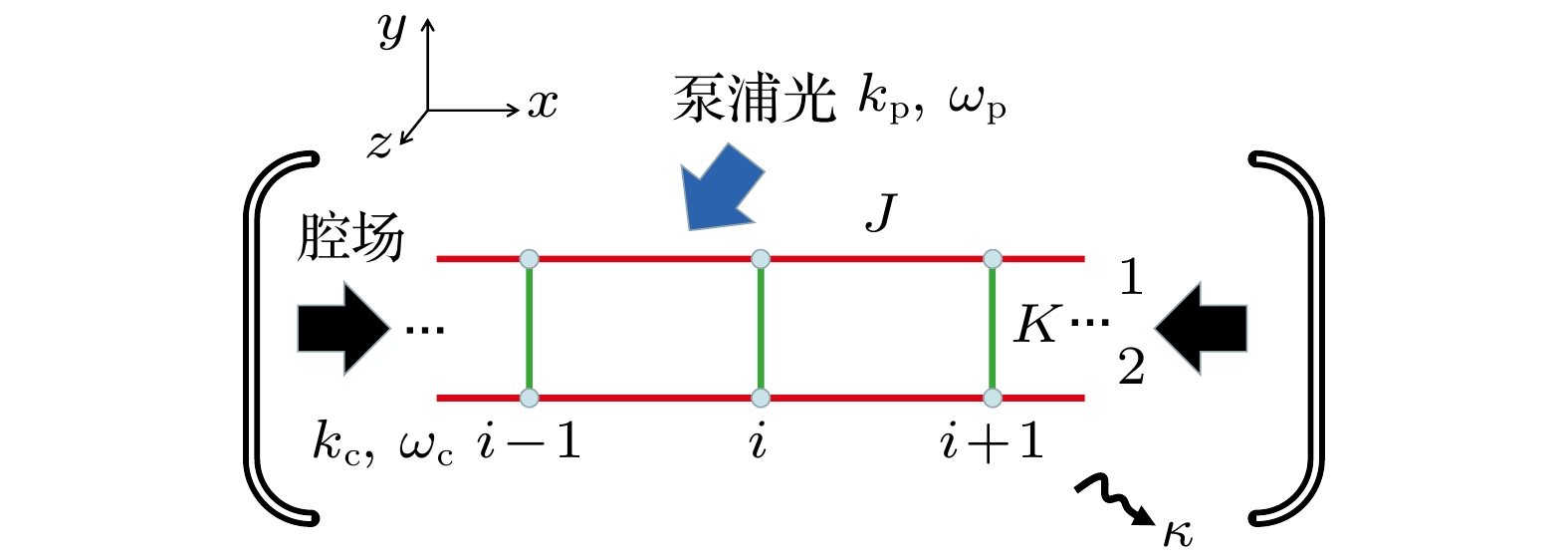
图 1 实验装置示意图. 在高精度腔中, 中性原子被x-y平面的梯子形光晶格俘获, 并沿着z方向加入驱动泵浦场. 泵浦场的频率为
$\omega_{\rm{p}}$ 远失谐于原子能级跃迁频率$\omega_{\rm{a}}$ , 但接近于腔场频率$\omega_{\rm{c}}$ Fig. 1. A schematic diagram of experimental setup. In a high-finesses optical cavity, spinless atoms are trapped by a ladder lattice in x-y plane. The atoms are driven by a pump laser beam along z direction. The frequency
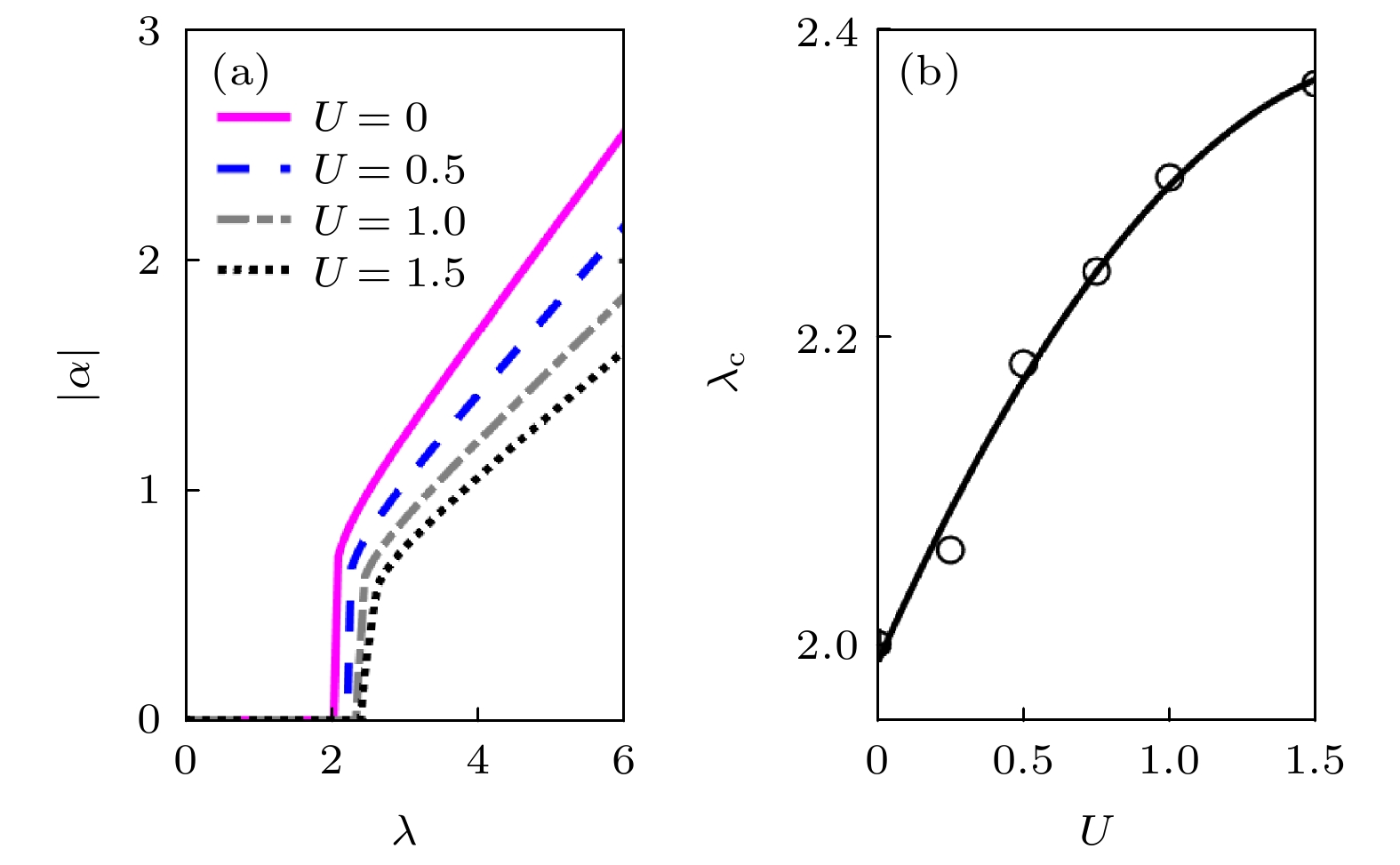
$ \omega_{\rm{p}} $ of the pump laser is far detuned from the atomic transition line$ \omega_{\rm{a}} $ but close to the cavity-mode frequency$ \omega_{\rm{c}} $ 
图 2 (a) 腔场耦合强度U取不同的值时, 光场
$ |\alpha| $ 随着耦合强度λ变化的图像; (b) 临界耦合强度$ \lambda_{\rm{c}} $ 随着U的变化情况. 这里,$ L = 1974 $ ,$ K = 0.8 $ ,$ \beta = 610/987 $ ,$ \varDelta_{{\rm{c}}} = -2 $ 和$ \kappa = 1.2 $ Fig. 2. (a) The cavity field
$ |\alpha| $ as a function of the pumping strength λ for different U; (b) the critical pumping strength$ \lambda_{\rm{c }}$ as a function of U. Here$ L = 1974 $ ,$ K = 0.8 $ ,$ \beta = 610/987 $ ,$ \varDelta_{{\rm{c}}} = -2 $ and$ \kappa = 1.2 $ 
图 3 (a) 当
$ U_{\rm{D}} = 1, K = 0.8, L = 3194 $ 时,$ \langle \text{IPR} \rangle $ (黑色实线) 和$ \langle \text{NPR} \rangle $ (红色虚线) 随$ \lambda_{\rm{D}} $ 变化的曲线, 灰色区域代表着具有迁移率边的临界区域; (b)$ \lambda_{\rm{D}} = 0.5 $ , (c)$ \lambda_{\rm{D}} = 2 $ , (d)$ \lambda_{\rm{D}} = 5 $ 时,$ \langle \text{NPR} \rangle $ 随着$ L^{-1} $ 的变化, 其余参数的取值是$ U_{\rm{D}} = 1 $ ,$ K = 0.8 $ Fig. 3. (a)
$ \langle \text{IPR} \rangle $ (the black solid line) and$ \langle \text{NPR} \rangle $ (the red dashed line) as the functions of$ \lambda_{\rm{D}} $ for$U_{\rm{D}} = 1, K = 0.8, $ $ L = 3194$ . The grey region denotes the critical region with mobility edges;$ \langle \text{NPR} \rangle $ as a function of$ L^{-1} $ with$ U_{\rm{D}} = 1 $ and$ K = 0.8 $ for (b)$ \lambda_{\rm{D}} = 0.5 $ , (c)$ \lambda_{\rm{D}} = 2 $ , and (d)$ \lambda_{\rm{D }}= 5 $ 
图 4 (a1)
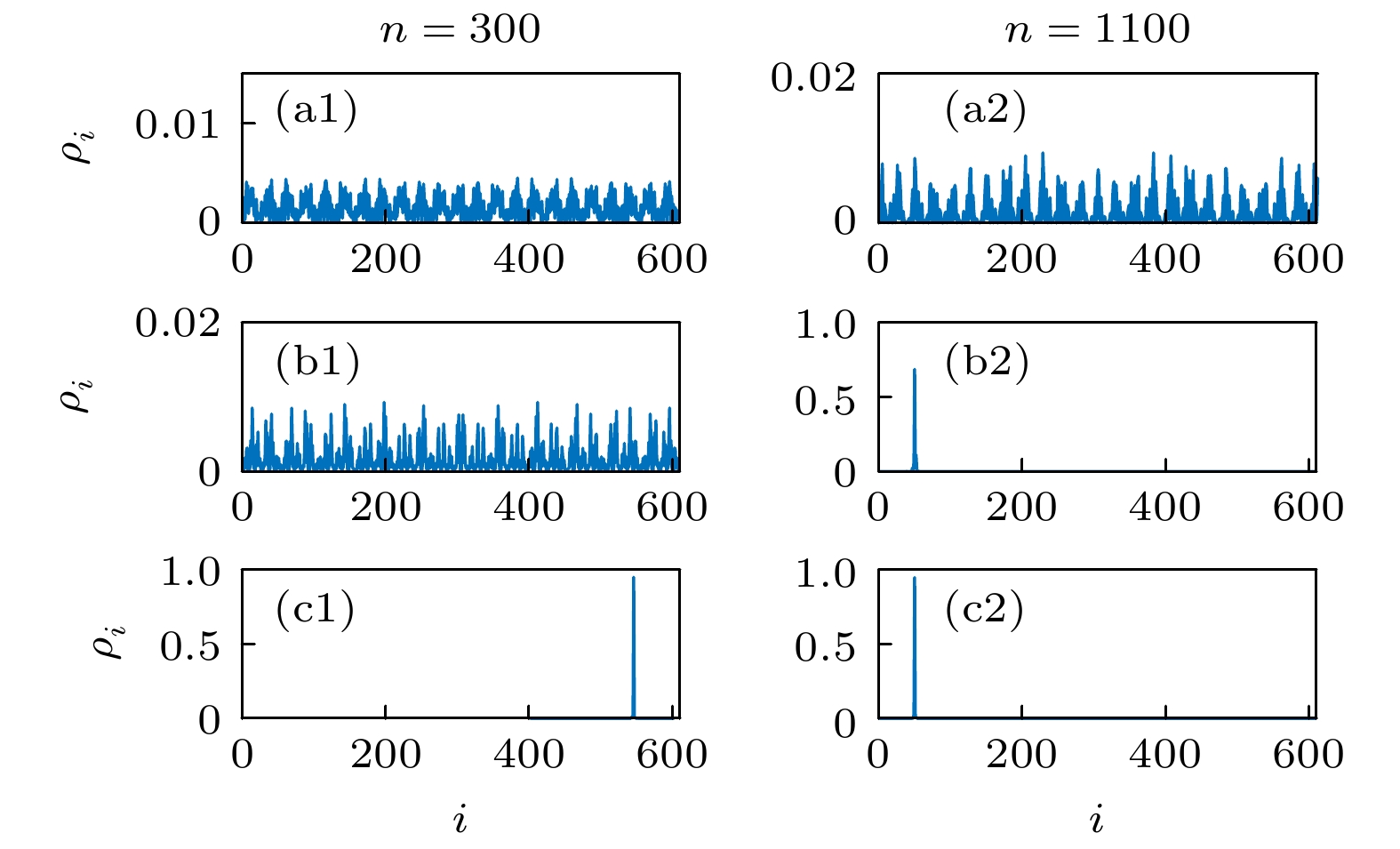
$ \lambda_{\rm{D}} = 0.5 $ , (b1)$ \lambda_{\rm{D}} = 2 $ 和(c1)$ \lambda_{\rm{D}} = 5 $ 时第300个激发态的密度分布; (a2)$ \lambda_{\rm{D }}= 0.5 $ , (b2)$ \lambda_{\rm{D}} = 2 $ 和(c2)$ \lambda_{\rm{D}} = 5 $ 时第 1100 个激发态的密度分布. 这里,$ K = 0.8 $ ,$ U_{\rm{D}} = 1 $ 和$ L = 1220 $ Fig. 4. Density distributions of the 300th excited eigenstates for (a1)
$ \lambda_{\rm{D}} = 0.5 $ , (b1)$ \lambda_{\rm{D}} = 2 $ , and (c1)$ \lambda_{\rm{D}} = 5 $ ; density distributions of the 1100th excited eigenstates for (a2)$ \lambda_{\rm{D}} = 0.5 $ , (b2)$ \lambda_{\rm{D }}= 2 $ , and (c2)$ \lambda_{\rm{D}} = 5 $ . Here,$ K = 0.8 $ ,$ U_{\rm{D}} = 1 $ , and$ L = 1220 $ 
图 5 在
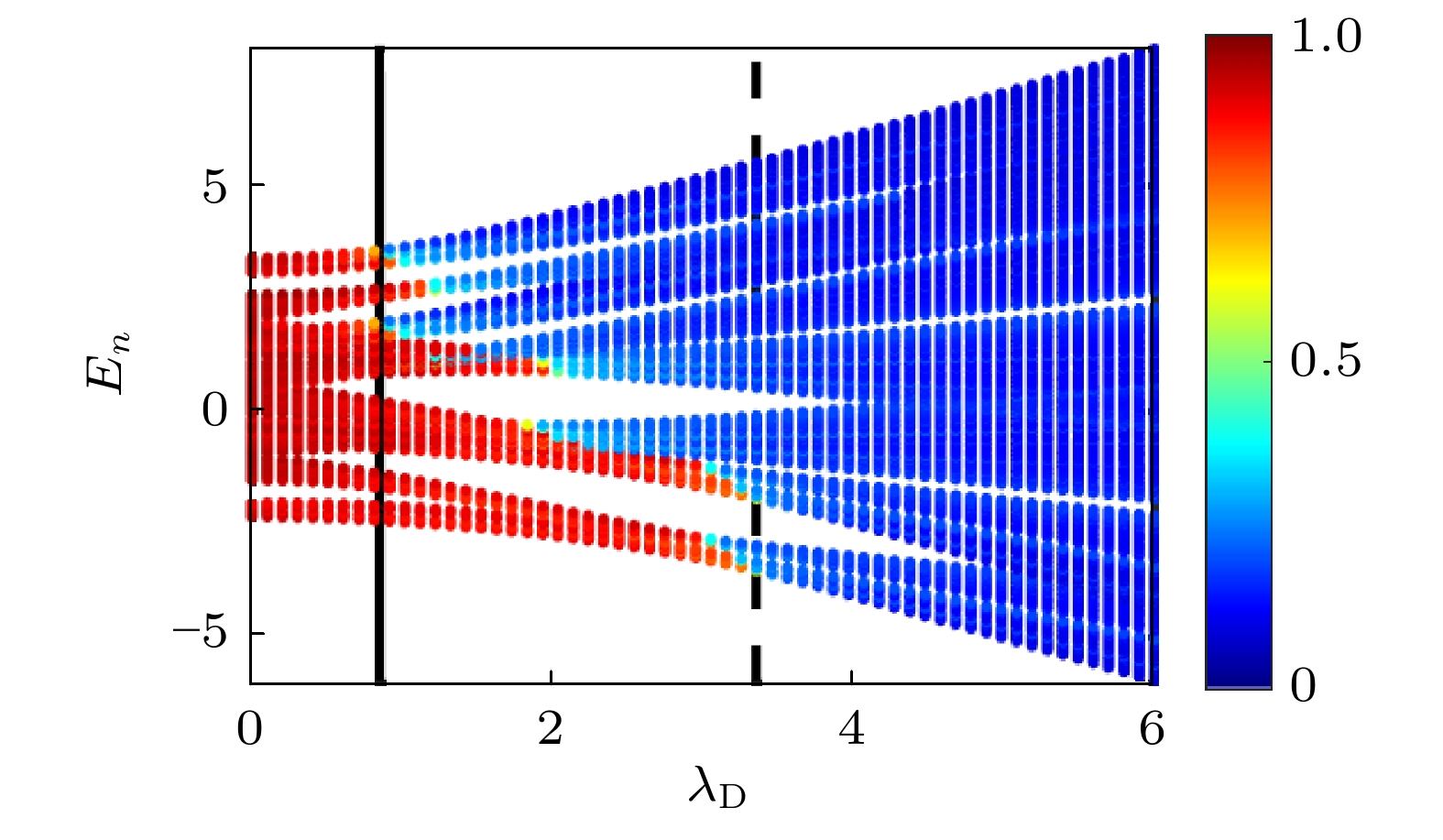
$ U_{\rm{D}} = 1 $ ,$ K = 0.8 $ 和$ L = 3194 $ 时, 分形维度γ随着调制强度$ \lambda_{\rm{D }}$ 和能量本征值$ E_n $ 的变化. 其中, 黑色实线和黑色虚线分别对应了两个局域化转变点$ \lambda_{\rm{D}}^{({\rm{c}}1)} $ 和$ \lambda_{\rm{D}}^{({\rm{c}}2)} $ . 图中颜色代表着γ的大小Fig. 5. γ of the eigenstates as a function of the energy spectrum and
$ \lambda_{\rm{D}} $ for$ U_{\rm{D}} = 1 $ ,$ K = 0.8 $ , and$ L = 3194 $ . Here the black solid line and black dashed line denote two transport points,$ \lambda_{\rm{D}}^{({\rm{c}}1)} $ and$ \lambda_{\rm{D}}^{({\rm{c}}2)} $ . The color code represents the values of γ
图 6 当
$ U_{\rm{D}} = 2, K = 0.8, L = 3194 $ 时 (a)$ \langle \text{IPR} \rangle $ (黑色实线)和$ \langle \text{NPR} \rangle $ (红色虚线)随着$ \lambda_{\rm{D}} $ 变化的曲线, 灰色区域表示具有迁移率边的临界相区; (b)分形维度γ随着能量本征值$ E_n $ 和调制强度$ \lambda_{\rm{D}} $ 的变化. 图中颜色代表γ的大小Fig. 6. (a)
$ \langle \text{IPR} \rangle $ (the black solid line) and$ \langle \text{NPR} \rangle $ (the red dashed line) as the functions of$ \lambda_{\rm{D}} $ for$U_{\rm{D}} = 2,\; K = 0.8, $ $ L = 3194$ . The grey regions denote the intermediate regimes with mobility edges; (b) fractal dimension γ of all the eigenstates as a function of energies and$ \lambda_{\rm{D}} $ for$U_{\rm{D}} = 2,$ $ K = 0.8 $ , and$ L = 3194 $ . Here the color code represents the values of γ
图 7 当
$ U_{\rm{D}} = 2 $ ,$ K = 0.8 $ 时平均参与率$ \langle \text{NPR} \rangle $ 随$ 1/L $ 变化的曲线 (a) 临界相区; (b) 局域相区Fig. 7.
$ \langle \text{NPR} \rangle $ as a function of$ 1/L $ for$ U_{\rm{D}} = 2 $ ,$K = 0.8 $ : (a) critical phase region; (b) localized phase region
图 8 (a)
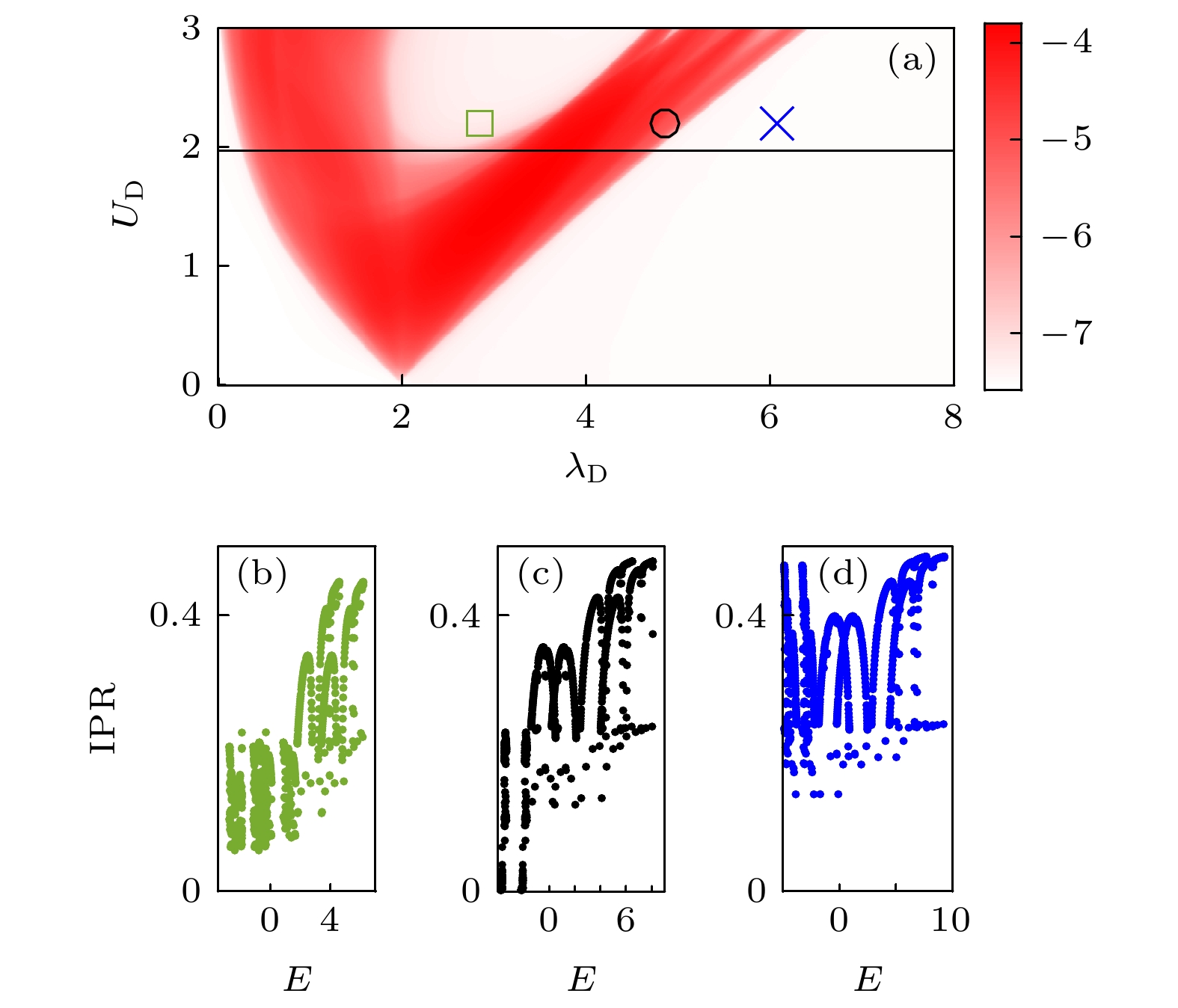
$\lambda_{\rm{D}}\text{-}U_{\rm{D}}$ 参数平面内, 以序参量η的大小为填充颜色的相图, 其中白色区域表示完全扩展或局域相, 红色区域表示具有迁移率边的临界相. 其中, 绿色方块对应$ \lambda = 3.183 $ ,$ \varDelta_{{\rm{c}}} = -0.2 $ ,$ |\alpha| = 0.604 $ ,$ \lambda_{{\rm{D}}}\approx2.86 $ ; 黑色圆圈对应的是$ \lambda = 4.113 $ ,$ \varDelta_{{\rm{c}}} = -0.6 $ ,$ |\alpha| = 0.607 $ ,$ \lambda_{{\rm{D}}}\approx4.86 $ ; 蓝色叉号对应于$ \lambda = 5.069 $ ,$ \varDelta_{{\rm{c}}} = -2 $ ,$ |\alpha| = 0.608 $ ,$ \lambda_{{\rm{D}}}\approx6.08 $ . 这里,$ \kappa = 1.2 $ ,$ U = 6 $ ,$ U_{\rm{D}}\approx2.21 $ . 相图中的(b)绿色方块, (c) 黑色圆圈和(d) 蓝色叉号对应的参数取值下, 所有态的逆参与率随本征能变化的情况. 这里,$ K = 0.8 $ 和$ L = 1974 $ Fig. 8. (a) Phase diagram in the
$\lambda_{\rm{D}}\text{-} U_{\rm{D}}$ plane. The color code represents the values of η, where the white regions denote the full extended or localized phase and the red region represents the critical phase. Here, the green square corresponds to$ \lambda = 3.183 $ ,$\varDelta_{{\rm{c}}} = -0.2$ ,$ |\alpha| = 0.604 $ ,$ \lambda_{{\rm{D}}}\approx2.86 $ , the black circle corresponds to$ \lambda = 4.113 $ ,$ \varDelta_{{\rm{c}}} = -0.6 $ ,$ |\alpha| = 0.607 $ ,$ \lambda_{{\rm{D}}}\approx4.86 $ , and the blue cross corresponds to$ \lambda = 5.069 $ ,$ \varDelta_{{\rm{c}}} = -2 $ ,$ |\alpha| = 0.608 $ ,$ \lambda_{{\rm{D}}}\approx6.08 $ for$ \kappa = 1.2 $ ,$ U = 6 $ ,$ U_{\rm{D}}\approx2.21 $ . The IPR of different eigenstates as a function of energies for (b) the green square, (c) the black circle, and (d) the blue cross. Here,$ K = 0.8 $ , and$ L = 1974 $ 
图 9 (a1)
$ K = 0.5 $ , (b1)$ K = 1.5 $ 时, 腔场耦合强度U取不同的值时, 光场$ |\alpha| $ 随着耦合强度λ变化的图像. 这里,$ L = 1974 $ ,$ \beta = 610/987 $ ,$\varDelta_{{\rm{c}}} = -2$ 和$ \kappa = 1.2 $ . (a2)$ K = 0.5 $ , (b2)$ K = 1.5 $ 时,$\lambda_{\rm{D}}-U_{\rm{D}}$ 参数平面内, 以序参量η的大小为填充颜色的相图, 其中白色区域表示完全扩展或局域相, 红色区域表示具有迁移率边的临界相. 这里,$ L = 1974 $ Fig. 9. The cavity field
$ |\alpha| $ as a function of the pumping strength λ for different U for (a1)$ K = 0.5 $ , (b1)$ K = 1.5 $ . Here$ L = 1974 $ ,$ \beta = 610/987 $ ,$\varDelta_{{\rm{c}}} = -2$ and$ \kappa = 1.2 $ . Phase diagram in the$\lambda_{\rm{D}}-U_{\rm{D}}$ plane with$ L = 1974 $ for (a2)$ K = 0.5 $ , (b2)$ K = 1.5 $ . The color code represents the values of η, where the white regions denote the full extended or localized phase and the red region represents the critical phase -
[1] Marklund M, Shukla P K 2006 Rev. Mod. Phys. 78 591
Google Scholar
[2] Chin C, Grimm R, Julienne P, Tiesinga E 2010 Rev. Mod. Phys. 82 1225
Google Scholar
[3] Mekhov I B, Maschler C, Ritsch H 2007 Nat. Phys. 3 319
Google Scholar
[4] Ritsch H, Domokos P, Brennecke F, Esslinger T 2013 Rev. Mod. Phys. 85 553
Google Scholar
[5] Baumann K, Guerlin C, Brennecke F, Esslinger T 2010 Nature 464 1301
Google Scholar
[6] Maschler C, Mekhov I B, Ritsch H 2008 Eur. Phys. J. D 46 545
Google Scholar
[7] Klinder J, Keβler H, Bakhtiari M R, Thorwart M, Hemmerich A 2015 Phys. Rev. Lett. 115 230403
Google Scholar
[8] Landig R, Hruby L, Dogra N, Landini M, Mottl R, Donner T, Esslinger T 2016 Nature 532 476
Google Scholar
[9] Zheng W, Cooper N R 2018 Phys. Rev. A 97 021601(R
Google Scholar
[10] Zhou L, Pu H, Zhang K Y, Zhao X D, Zhang W P 2011 Phys. Rev. A 84 043606
Google Scholar
[11] Habibian H, Winter A, Paganelli S, Rieger H, Morigi G 2013 Phys. Rev. Lett. 110 075304
Google Scholar
[12] Anderson P W 1958 Phys. Rev. 109 1492
Google Scholar
[13] Aubry S, André G 1980 Ann. Isr.: Phys. Soc. 3 18
[14] Roati G, D’Errico C, Fallani L, Fattori M, Fort C, Zaccanti M, Modugno G, Modugno M, Inguscio M 2008 Nature 453 895
Google Scholar
[15] Sarma S D, Kobayashi A, Prange R E 1986 Phys. Rev. Lett. 56 1280
Google Scholar
[16] Sarma S D, Song H, Xie X C 1988 Phys. Rev. Lett. 61 2144
Google Scholar
[17] Biddle J, Sarma S D 2010 Phys. Rev. Lett. 104 070601
Google Scholar
[18] Ganeshan S, Pixley J H, Sarma S D 2015 Phys. Rev. Lett. 114 146601
Google Scholar
[19] Lanini Y, Bromberg Y, Christodoulides D N, Silberberg Y 2010 Phys. Rev. Lett. 105 163905
Google Scholar
[20] Xu Z H, Xia X, Chen S 2021 arXiv: 2109.02072 v1[cond-mat.dis-nn]
[21] Wang Y C, Xia X, Wang Y J, Zheng Z H, Liu X J 2021 Phys. Rev. B 103 174205
Google Scholar
[22] 徐志浩, 皇甫宏丽, 张云波 2019 68 087201
Google Scholar
Xu Z H, Huangfu H L, Zhang Y B 2019 Acta Phys. Sin. 68 087201
Google Scholar
[23] Xu Z H, Xia X, Chen S 2022 Sci. China-Phys. Mech. Astron. 65 227211
Google Scholar
[24] Roy S, Mishra T, Tanatar B, Basu S 2021 Phys. Rev. Lett 126 106803
Google Scholar
[25] Jiang X P, Qiao Y, Cao J P 2021 Chin. Phys. B 30 097202
Google Scholar
[26] Padhan A, Giri M K, Mondal S, Mishra T 2021 arXiv: 2109.09621 v1 [cond-mat.quant-gas]
[27] Zhuang W F, Geng B, Lou H G, Guo G C, Gong M 2021 Phys. Rev. A 104 053308
Google Scholar
[28] Keeling J, Bhaseen M J, Simons B D 2014 Phys. Rev. Lett 112 143002
Google Scholar
[29] Piazza F, Strack P 2014 Phys. Rev. Lett. 112 143003
Google Scholar
[30] Chen Y, Yu Z H, Zhai H 2014 Phys. Rev. Lett. 112 143004
Google Scholar
[31] Chen Y, Zhai H, Yu Z H 2015 Phys. Rev. A 91 021602(R
Google Scholar
[32] Chen Y, Yu Z H, Zhai H 2016 Phys. Rev. A 93 041601(R
Google Scholar
[33] Cai M L, Liu Z D, Zhao W D, Wu Y K, Mei Q X, Jiang Y, He L, Zhang X, Zhou Z C, Duan L M 2021 Nat. Commun. 12 1126
Google Scholar
[34] Xu Z H, Chen S 2021 Phys. Rev. A 103 043325
Google Scholar
下载:
计量
- 文章访问数: 4734
- PDF下载量: 174
- 被引次数: 0
