-
冷原子重力仪正逐渐向小型化、动态化、实用化方向发展, 将其应用于深远海绝对重力测量及水下长航时、高精度导航具有十分重要的意义. 而目前冷原子重力仪多数尚处于实验室静基座或准静基座测量状态, 难以满足动态应用场景下的重力测量需求, 因此对冷原子干涉重力测量进行“由静到动”的相关研究十分迫切和关键. 本文分析了动态测量的基本原理, 给出了冷原子重力仪与加速度计组合测量的基本方法, 搭建了一套基于冷原子重力仪和惯性稳定平台绝对动态重力测量系统, 并采用冷原子重力仪与传统加速度计组合测量方式, 开展了船载动态测量实验. 首先, 在实验室静态环境下进行了约40 h的连续绝对重力测量, 对冷原子重力仪的性能进行初步评估, 灵敏度为447 µGal/
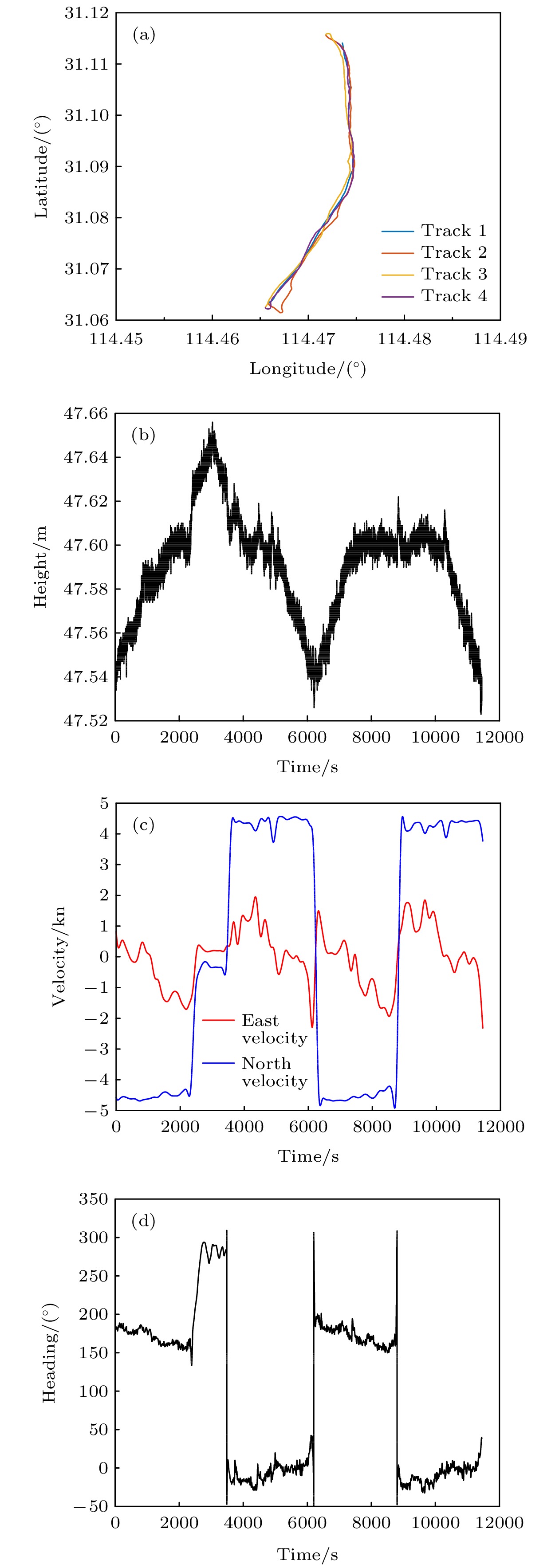
$\sqrt {{\text{Hz}}} $ (1 Gal = 1 cm/s2), 长期稳定度可达2.7 µGal. 在此基础上开展船载实验, 测量船在湖上以约4.6 kn的速度航行, 采用重复测线的方式开展了船载绝对动态重力测量. 经评估, 四条重复测线的内符合精度为2.272 mGal, 四个航次外符合精度分别为2.331, 1.837, 3.988和2.589 mGal. 最后, 针对实验结果, 对可能存在的问题进行进一步分析与总结. 本实验研究为海洋绝对重力动态测量提供了前期验证与技术方案参考.Cold atom gravimeter is gradually developing towards miniaturization, dynamics and practicality. It is of great significance to apply it to deep and far sea absolute gravity measurement and underwater long navigation time and high-precision navigation. At present, most cold atom gravimeters are still in the state of laboratory static base or quasi-static base measurement, which is difficult to meet the gravity measurement needs in dynamic application scenarios. Therefore, the research on "static to dynamic" of cold atom interferometric gravity measurement is very urgent and key. In this paper, the basic principle of dynamic measurement is analyzed, the basic method of combined measurement of cold atom gravimeter and accelerometer is given, a set of absolute dynamic gravity measurement system based on cold atom gravimeter and inertial stabilization platform is built, and the ship-borne dynamic measurement experiment is carried out by using the combined measurement method of cold atom gravimeter and traditional accelerometer. Firstly, the continuous absolute gravity measurement for about 40 h is carried out in the laboratory static environment to preliminarily evaluate the performance of the cold atom gravimeter. The sensitivity is 447 µGal/$\sqrt {{\text{Hz}}} $ , and the long-term stability can reach 2.7 µgal. On this basis, the ship-borne experiment is conducted, the survey ship sails on the lake at a speed of about 4.6 kn, and the ship-borne absolute dynamic gravity measurement is carried out by means of repeated survey lines. After evaluation, the internal coincidence accuracy of the four repeated survey lines is 2.272 mGal, and the external coincidence accuracy values of the four voyages are 2.331, 1.837, 3.988 and 2.589 mGal respectively. Finally, according to the experimental results, the possible problems are further analyzed and summarized. This experimental study provides preliminary verification and technical scheme reference for marine absolute dynamic gravity measurement.[1] Bongs K, Holynski M, Vovrosh J, Bouyer P, Condon G, Rasel E, Schubert C, Schleich W P, Roura A 2019 Nat. Rev. Phys. 1 731
Google Scholar
[2] 房丰洲, 顾春阳 2017 仪器仪表学报 38 081830
Fang F Z, Gu C Y 2017 Chin. J. Sci. Instrum. 38 081830
[3] 李安, 车浩, 覃方君, 黄春福, 龚文斌 2021 海军工程大学学报 33 0601
Li A, Che H, Qin F J, Huang C F, Gong W B 2021 J. Nav. Univ. Eng. 33 0601
[4] Geiger R, Landragin A, Merlet S, Santos F P D 2020 AVS Quantum Sci. 2 024702
Google Scholar
[5] Peters A, Chung K Y, Chu S 2001 Metrologia 38 25
Google Scholar
[6] Schmidt M, Prevedelli M, Giorgini A, Tino G M, Peters A 2011 Appl. Phys. B 102 11
Google Scholar
[7] Bidel Y, Carraz O, Charriere R, Cadoret M, Zahzam N, Bresson A 2013 Appl. Phys. Lett. 102 144107
Google Scholar
[8] Wu X J, Pagel Z, Malek B S, Nguyen T H, Zi F, Scheirer D S, Muller H 2019 Sci. Adv. 5 eaax0800
Google Scholar
[9] Zhang J Y, Chen L L, Cheng Y, Luo Q, Shu Y B, Duan X C, Zhou M K, Hu Z K 2020 Chin. Phys. B 29 093702
Google Scholar
[10] Bidel Y, Zahzam N, Blanchard C, Bonnin A, Cadoret M, Bresson A, Rouxel D, Lequentrec-Lalancette M F 2018 Nat. Commun. 9 9
Google Scholar
[11] Bidel Y, Zahzam N, Bresson A, Blanchard C, Cadoret M, Olesen A V, Forsberg R 2020 J. Geod. 94 2
Google Scholar
[12] Zhang J Y, Xu W J, Sun S D, Shu Y B, Luo Q, Cheng Y, Hu Z K, Zhou M K 2021 AIP Adv. 11 115223
Google Scholar
[13] 吴彬, 周寅, 程冰, 朱栋, 王凯楠, 朱欣欣, 陈佩军, 翁堪兴, 杨秋海, 林佳宏, 张凯军, 王河林, 林强 2020 69 060302
Google Scholar
Wu B, Zhou Y, Cheng B, Zhu D, Wang K N, Zhu X X, Chen P J, Weng K X, Yang Q H, Lin J H, Zhang K J, Wang H L, Lin Q 2020 Acta Phys. Sin. 69 060302
Google Scholar
[14] 程冰, 周寅, 陈佩军, 张凯军, 朱栋, 王凯楠, 翁堪兴, 王河林, 彭树萍, 王肖隆, 吴彬, 林强 2021 70 040304
Google Scholar
Cheng B, Zhou Y, Chen P J, Zhang K J, Zhu D, Wang K N, Weng K X, Wang H L, Peng S P, Wang X L, Wu B, Lin Q 2021 Acta Phys. Sin. 70 040304
Google Scholar
[15] 程冰, 陈佩军, 周寅, 王凯楠, 朱栋, 楚立, 翁堪兴, 王河林, 彭树萍, 王肖隆, 吴彬, 林强 2022 71 026701
Google Scholar
Cheng B, Chen P J, Zhou Y, Wang K N, Zhu D, Chu li, Weng K X, Wang H L, Peng S P, Wang X L, Wu B, Lin Q 2022 Acta Phys. Sin. 71 026701
Google Scholar
[16] Le Gouët J, Mehlstaubler T E, Kim J, Merlet S, Clairon A, Landragin A, Dos Santos F P 2008 Appl. Phys. B 92 133
Google Scholar
[17] Cheinet P, Canuel B, Pereira D S F, Gauguet A, Leduc F, Landragin A 2008 IEEE Trans. Instrum. Meas. 57 1141
Google Scholar
[18] Tang B, Zhou L, Xiong Z Y, Wang Jin, Zhan M S A 2014 Rev. Sci. Instrum. 85 123
Google Scholar
[19] Rakholia A V 2015 Ph. D. Dissertation (New Mexico: The University of New Mexico)
[20] Merlet S, Le Gouët J, Bodart Q, Clairon A, Rouchon P 2009 Metrologia 46 87
Google Scholar
[21] 罗东云, 程冰, 周寅, 吴彬, 王肖隆, 林强 2018 67 020702
Google Scholar
Luo D Y, Cheng B, Zhou Y, Wu B, Wang X L, Lin Q 2018 Acta Phys. Sin. 67 020702
Google Scholar
[22] Cheiney P, Fouche L, Templier S, Napolitano F, Battelier B, Bouyer P, Barrett B 2018 Phys. Rev. Appl. 10 034030
Google Scholar
[23] Cheiney P, Barrett B, Templier S, Jolly O, Napolitano F 2019 IEEE International Symposium on Inertial Sensors and Systems(INERTIAL) Naples FL, USA, April 1–5, 2019 p1
[24] Fang J, Hu J G, Chen X, Zhu H R, Zhou L, Zhong J Q, Wang J, Zhan M S 2018 Opt. Express 26 1586
Google Scholar
-
图 1 冷原子重力仪/加速度计组合测量原理示意图
Fig. 1. Principal of combined measurement of cold atom gravimeter/accelerometer.
图 2 实验装置及航迹 (a) 冷原子重力仪与dgShip型重力仪; (b) CG-5型重力仪; (c)实验测量船; (d)计划航线
Fig. 2. Experimental device and route: (a) Cold atom gravimeter and dgShip gravimeter; (b) CG-5 gravimeter; (c) experimental measuring ship; (d) planned route.
图 4 实验室静基座测量结果 (a) 重力测量值; (b) Allan方差
Fig. 4. Laboratory static measurement: (a) Gravity measurements; (b) Allan variance.
图 5 运动参数 (a) 航行轨迹; (b) 载体高度; (c) 航行速度; (d) 载体航向
Fig. 5. Motion parameters: (a) Trajectory; (b) height; (c) velocity; (d) heading.
图 6 绝对重力测量数据 (a) 原始数据; (b) 低通滤波后; (c) Eötvös校正后
Fig. 6. Absolute gravimetry data: (a) Raw data; (b) low pass filtered; (c) Eötvös corrected.
图 7 干涉条纹 (a) 补偿前条纹(正啁啾); (b) 补偿后条纹(正啁啾); (c) 补偿前条纹(负啁啾); (d) 补偿后条纹(负啁啾)
Fig. 7. Interference fringes: (a) Before compensation(positive chirp); (b) after compensation (positive chirp); (c) before compensation(negative chirp); (d) after compensation(negative chirp).
表 1 实验系统主要硬件设备及功能
Table 1. Main hardware equipment and functions of the experimental system.
类别 名称 规格 功能 重力仪及
配套装置冷原子重力仪 1套 绝对重力测量 dgShip型重力仪 1套 高精度动态相对重力测量, 提供动态重力基准比对 CG-5型重力仪 1台 高精度静态相对重力测量, 提供静态重力基准参考 笔记本电脑 1台 冷原子重力仪数据采集与处理 传统加速度计 1支 置于拉曼光反射镜下, 与冷原子重力仪进行组合测量 惯性稳定平台
及配套装置双轴惯性稳定平台 1套 提供稳定的水平基准和姿态信息, 保持冷原子重力仪系统稳定的垂直指向 高精度惯性导航系统 1套 与GPS组合测量, 获取航行过程中的速度、位置、姿态等信息 差分GPS装置 1套 获取载体位置信息, 与惯性稳定平台组合 减振装置 1套 置于稳定平台底部, 减少稳定平台的振动 电源系统 1套 为实验设备供电 
下载: 导出CSV
-
[1] Bongs K, Holynski M, Vovrosh J, Bouyer P, Condon G, Rasel E, Schubert C, Schleich W P, Roura A 2019 Nat. Rev. Phys. 1 731
Google Scholar
[2] 房丰洲, 顾春阳 2017 仪器仪表学报 38 081830
Fang F Z, Gu C Y 2017 Chin. J. Sci. Instrum. 38 081830
[3] 李安, 车浩, 覃方君, 黄春福, 龚文斌 2021 海军工程大学学报 33 0601
Li A, Che H, Qin F J, Huang C F, Gong W B 2021 J. Nav. Univ. Eng. 33 0601
[4] Geiger R, Landragin A, Merlet S, Santos F P D 2020 AVS Quantum Sci. 2 024702
Google Scholar
[5] Peters A, Chung K Y, Chu S 2001 Metrologia 38 25
Google Scholar
[6] Schmidt M, Prevedelli M, Giorgini A, Tino G M, Peters A 2011 Appl. Phys. B 102 11
Google Scholar
[7] Bidel Y, Carraz O, Charriere R, Cadoret M, Zahzam N, Bresson A 2013 Appl. Phys. Lett. 102 144107
Google Scholar
[8] Wu X J, Pagel Z, Malek B S, Nguyen T H, Zi F, Scheirer D S, Muller H 2019 Sci. Adv. 5 eaax0800
Google Scholar
[9] Zhang J Y, Chen L L, Cheng Y, Luo Q, Shu Y B, Duan X C, Zhou M K, Hu Z K 2020 Chin. Phys. B 29 093702
Google Scholar
[10] Bidel Y, Zahzam N, Blanchard C, Bonnin A, Cadoret M, Bresson A, Rouxel D, Lequentrec-Lalancette M F 2018 Nat. Commun. 9 9
Google Scholar
[11] Bidel Y, Zahzam N, Bresson A, Blanchard C, Cadoret M, Olesen A V, Forsberg R 2020 J. Geod. 94 2
Google Scholar
[12] Zhang J Y, Xu W J, Sun S D, Shu Y B, Luo Q, Cheng Y, Hu Z K, Zhou M K 2021 AIP Adv. 11 115223
Google Scholar
[13] 吴彬, 周寅, 程冰, 朱栋, 王凯楠, 朱欣欣, 陈佩军, 翁堪兴, 杨秋海, 林佳宏, 张凯军, 王河林, 林强 2020 69 060302
Google Scholar
Wu B, Zhou Y, Cheng B, Zhu D, Wang K N, Zhu X X, Chen P J, Weng K X, Yang Q H, Lin J H, Zhang K J, Wang H L, Lin Q 2020 Acta Phys. Sin. 69 060302
Google Scholar
[14] 程冰, 周寅, 陈佩军, 张凯军, 朱栋, 王凯楠, 翁堪兴, 王河林, 彭树萍, 王肖隆, 吴彬, 林强 2021 70 040304
Google Scholar
Cheng B, Zhou Y, Chen P J, Zhang K J, Zhu D, Wang K N, Weng K X, Wang H L, Peng S P, Wang X L, Wu B, Lin Q 2021 Acta Phys. Sin. 70 040304
Google Scholar
[15] 程冰, 陈佩军, 周寅, 王凯楠, 朱栋, 楚立, 翁堪兴, 王河林, 彭树萍, 王肖隆, 吴彬, 林强 2022 71 026701
Google Scholar
Cheng B, Chen P J, Zhou Y, Wang K N, Zhu D, Chu li, Weng K X, Wang H L, Peng S P, Wang X L, Wu B, Lin Q 2022 Acta Phys. Sin. 71 026701
Google Scholar
[16] Le Gouët J, Mehlstaubler T E, Kim J, Merlet S, Clairon A, Landragin A, Dos Santos F P 2008 Appl. Phys. B 92 133
Google Scholar
[17] Cheinet P, Canuel B, Pereira D S F, Gauguet A, Leduc F, Landragin A 2008 IEEE Trans. Instrum. Meas. 57 1141
Google Scholar
[18] Tang B, Zhou L, Xiong Z Y, Wang Jin, Zhan M S A 2014 Rev. Sci. Instrum. 85 123
Google Scholar
[19] Rakholia A V 2015 Ph. D. Dissertation (New Mexico: The University of New Mexico)
[20] Merlet S, Le Gouët J, Bodart Q, Clairon A, Rouchon P 2009 Metrologia 46 87
Google Scholar
[21] 罗东云, 程冰, 周寅, 吴彬, 王肖隆, 林强 2018 67 020702
Google Scholar
Luo D Y, Cheng B, Zhou Y, Wu B, Wang X L, Lin Q 2018 Acta Phys. Sin. 67 020702
Google Scholar
[22] Cheiney P, Fouche L, Templier S, Napolitano F, Battelier B, Bouyer P, Barrett B 2018 Phys. Rev. Appl. 10 034030
Google Scholar
[23] Cheiney P, Barrett B, Templier S, Jolly O, Napolitano F 2019 IEEE International Symposium on Inertial Sensors and Systems(INERTIAL) Naples FL, USA, April 1–5, 2019 p1
[24] Fang J, Hu J G, Chen X, Zhu H R, Zhou L, Zhong J Q, Wang J, Zhan M S 2018 Opt. Express 26 1586
Google Scholar
下载:
计量
- 文章访问数: 6383
- PDF下载量: 216
- 被引次数: 0
