电子非麦氏分布的二次电子发射磁化鞘层特性

陈龙; 孙少娟; 姜博瑞; 段萍; 安宇豪; 杨叶慧

doi:10.7498/aps.70.20211061

摘要

采用空间一维速度三维的磁流体模型研究了电子的非麦克斯韦分布对具有二次电子发射的磁化等离子体鞘层特性的影响. 假设鞘层中电子速度服从非广延分布, 离子在具有一定倾斜角度的磁场中被磁化. 通过建立自洽的磁流体方程, 研究了电子非广延分布参数q及磁场强度和角度对等离子体鞘层玻姆判据、壁面悬浮电势、鞘边二次电子数密度、鞘层厚度、离子速度等的影响. 研究表明, 当电子速度分布偏离麦克斯韦分布时, 非广延参数q值越大, 玻姆判据的值越小, 壁面电势越高, 鞘边二次电子数密度增大, 鞘层厚度减小, 鞘层区域离子、电子数密度下降加快, 且壁面附近离子数密度较高, 离子3个方向的速度均降低. 此外, 随着磁场强度增大, 鞘层厚度减小, 鞘层区域离子、电子数密度下降加快; 磁场角度越大, 参数q值对壁面电势、鞘层厚度的影响程度越显著, 在超广延、亚广延分布情况下壁面附近离子x方向速度随磁场角度变化呈相反趋势.

关键词:

Abstract

In this paper, the effects of non-Maxwellian distribution of electrons on the characteristics of magnetized plasma sheath with secondary electron emission are investigated by using a magnetic fluid model of one-dimensional velocity and three-dimensional space. The velocity of electrons follows the non-extensive distribution, and the ions are magnetized in a magnetic field with a certain tilt angle relative to the wall. The effects of the non-extensive electron distribution parameter q and the magnetic field strength and angle on the Bohm criterion, the floating wall potential, the secondary electron number density at the sheath edge, the sheath thickness and the ion velocity are studied by establishing the self-consistent equations. When the electron velocity distribution deviates from the Maxwellian distribution, the results show that as the q-parameter increases, the value of the Bohm criterion decreases, the floating wall potential increases, the number of secondary electrons at the sheath increases, the sheath thickness decreases, the number density of ions and electrons decline faster, the number density of ions near the wall is higher, and the velocities of the ions in the three directions are all reduced. In addition, as the magnetic field strength increases, the sheath thickness decreases, and the number density of ions and electrons in the sheath area decrease rapidly; the larger the magnetic field angle, the more significant the influences of the parameter q on the wall potential and the sheath thickness are, while the velocity component of the ion in the x-direction decreases with the increase of the magnetic field angle, but in the case of super-extensive distribution (q < 1), the velocity change near the wall presents an opposite trend, the increase of magnetic field angle causes wall velocity to increase; when it is close to Maxwellian distribution (q → 1), the velocity near the wall does not depend on the change of the magnetic field angle and basically tends to be identical; in the case of sub-extensive distribution (q > 1), the velocity near the wall decreases with the magnetic field angle increasing.

Keywords:

作者及机构信息

大连海事大学理学院, 大连　116026

通信作者: 段萍, duanping@dlmu.edu.cn

基金项目: 国家自然科学基金(批准号: 11975062, 11605021, 11975088)和中国博士后科学基金(2017M621120)资助的课题.

Authors and contacts

School of Science, Dalian Maritime University, Dalian 116026, China

Corresponding author: Duan Ping, duanping@dlmu.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant Nos. 11975062, 11605021, 11975088) and the China Postdoctoral Science Foundation (Grant No. 2017M621120).

文章全文 : translate this paragraph

参考文献

[1]	Franklin R N 2000 J. Phys. D: Appl. Phys. 33 3186 Google Scholar
[2]	Tskhakaya D D, Shukla P K, Eliasson B, Kuhn S 2005 Phys. Plasmas 12 103503 Google Scholar
[3]	Shibata K, Ito H, Yugami N, Miyazaki T, Nishida Y 2001 Thin Solid Films 386 291 Google Scholar
[4]	Hatami M M 2015 Phys. Plasmas 22 023506 Google Scholar
[5]	Aanesland A, Rafalskyi D, Bredin J, Grondein P, Oudini N, Chabert P, Levko D, Garrigues L, Hagelaar G 2015 IEEE Trans. Plasma Sci. 43 321 Google Scholar
[6]	Adhikari S, Moulick R, Goswami K S 2017 Phys. Plasmas 224 083501 Google Scholar
[7]	Liu J Y, Zhang Q, Zou X, Wang Z X, Liu Y, Wang X G, Gong Y 2004 Vacuum 73 687 Google Scholar
[8]	Driouch I, Chatei H, Bojaddaini M E 2015 Phys. Plasmas 81 905810104 Google Scholar
[9]	Benlemdjaldi D, Tahraoui A, Hugon R, Bougdira J 2013 Phys. Plasmas 20 043508 Google Scholar
[10]	王正汹, 刘金远, 邹秀, 刘悦, 王晓刚 2004 53 793 Google Scholar Wang Z X, Liu J Y, Zou X, Liu Y, Wang X G 2004 Acta Phys. Sin. 53 793 Google Scholar
[11]	Saslaw W C, Arp H 1986 Phys. Today 39 61 Google Scholar
[12]	Cáceres M O 1999 Braz. J. Phys. 29 125 Google Scholar
[13]	Tsallis C, Mendes R, Plastino A R 1998 Physica A 261 534 Google Scholar
[14]	Hatami M M, Tribeche M 2018 IEEE Trans. Plasma Sci. 46 868 Google Scholar
[15]	Meige A, Boswell R W 2006 Phys. Plasmas 13 92104 Google Scholar
[16]	Singh H, Graves D B 2000 J. Appl. Phys. 88 3889 Google Scholar
[17]	Tsallis C 1988 J. Stat. Phys. 52 479 Google Scholar
[18]	Borgohain D R, Saharia K, Goswami K S 2016 Phys. Plasmas 23 122113 Google Scholar
[19]	Driouch I, Chatei H 2017 Eur. Phys. J. D. 71 1 Google Scholar
[20]	Hatami M M, Tribeche M, Mamun A A 2018 Phys. Plasmas 25 094502 Google Scholar
[21]	Hatami M M, Tribeche M, Mamun A A 2019 Astrophysics Space Sci. 364 1 Google Scholar
[22]	Zhao X Y, Zhang B K, Wang C X 2020 Phys. Plasmas 27 113705 Google Scholar
[23]	Safa N N, Ghomi H, Niknam A R 2014 Phys. Plasmas 21 082111 Google Scholar
[24]	Basnet S, Khanal R 2019 Phys. Plasmas 26 043516 Google Scholar
[25]	Zou X, Liu H P, Zhu Y Z, Zang X N, Qiu M H 2020 Plasmas Sci. Technol. 22 125001 Google Scholar
[26]	Dhawan R, Kumar M, Malik H K 2020 Phys. Plasmas 27 063515 Google Scholar
[27]	Basnet S, Patel A, Khanal R 2020 Plasma Phys. Control. Fusion 62 115011 Google Scholar
[28]	赵晓云, 张丙开, 王春晓, 唐义甲 2019 68 185204 Google Scholar Zhao X Y, Zhang B K, Wang C X, Tang Y J 2019 Acta Phys. Sin. 68 185204 Google Scholar
[29]	Ghani O E, Driouch I, Chatei H 2020 Phys. Plasmas 27 083701 Google Scholar
[30]	邹秀, 刘惠平, 张小楠, 邱明辉 2021 70 015201 Google Scholar Zou X, Liu H P, Zhang X N, Qiu M H 2021 Acta Phys. Sin. 70 015201 Google Scholar
[31]	Dhawan R, Malik H K 2021 Plasmas Sci. Technol. 23 045402 Google Scholar
[32]	Bezerra J R, Silva R, Lima J A S 2003 Physica A 322 256 Google Scholar
[33]	Safa N N, Ghomi H, Niknam A R 2015 Phys. Plasmas 81 905810303 Google Scholar
[34]	Borgohain D R, Saharia K 2018 Phys. Plasmas 25 032122 Google Scholar
[35]	Tribeche M, Djebarni L, Amour R 2010 Phys. Plasmas 17 042114 Google Scholar
[36]	Hatami M M 2015 Phys. Plasmas 22 013508 Google Scholar
[37]	Chen F F 1974 Introduction to Plasma Physics (New York: Springer Science)

施引文献

图 1 等离子体磁鞘示意图

Fig. 1. Schematic diagram of the magnetized plasma sheath.

下载: 全尺寸图片幻灯片

图 2 不同非广延参数q下的电子速度分布及其对电子数密度的影响　(a)电子速度非广延分布; (b)电子数密度分布

Fig. 2. Electron velocity distribution and its influence on electron number density under different non-extensive parameter q: (a) Normalized velocity non-extensive distribution of electron; (b) electron number density distribution.

下载: 全尺寸图片幻灯片

图 3 玻姆判据随非广延参数q的变化　(a) q < 1; (b) q > 1

Fig. 3. Bohm criterion versus non-extensive parameter q: (a) q < 1; (b) q > 1.

下载: 全尺寸图片幻灯片

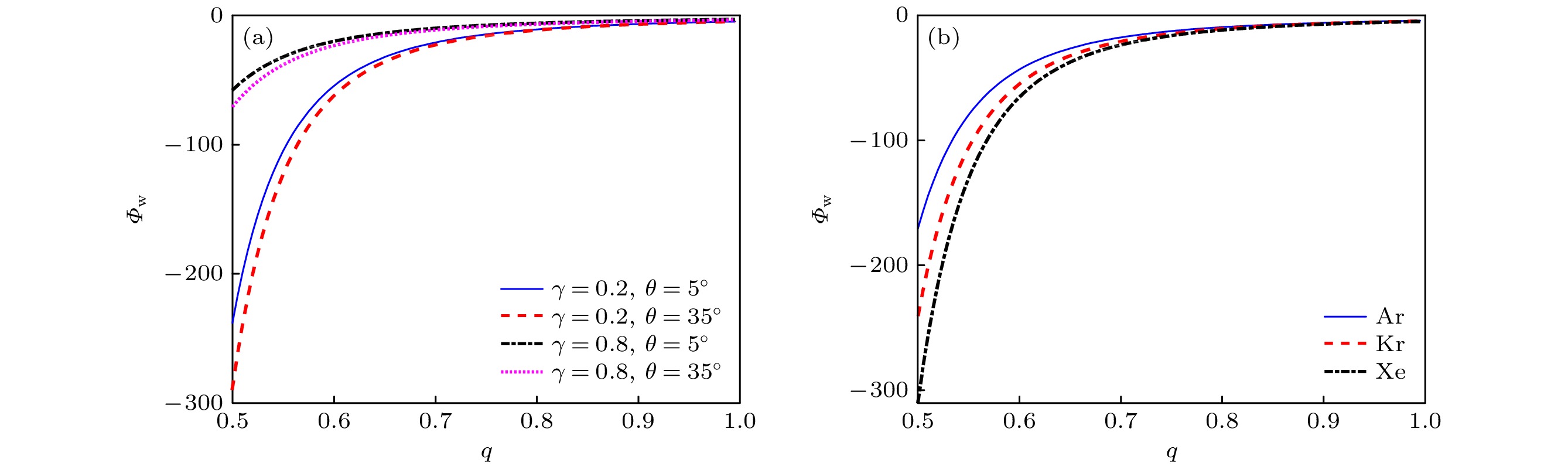
图 4 壁面电势随非广延参数q的变化　(a)不同$ \gamma, \theta $对$ {\varPhi }_{\mathrm{w}} $的影响; (b)不同等离子体种类对$ {\varPhi }_{\mathrm{w}}$的影响

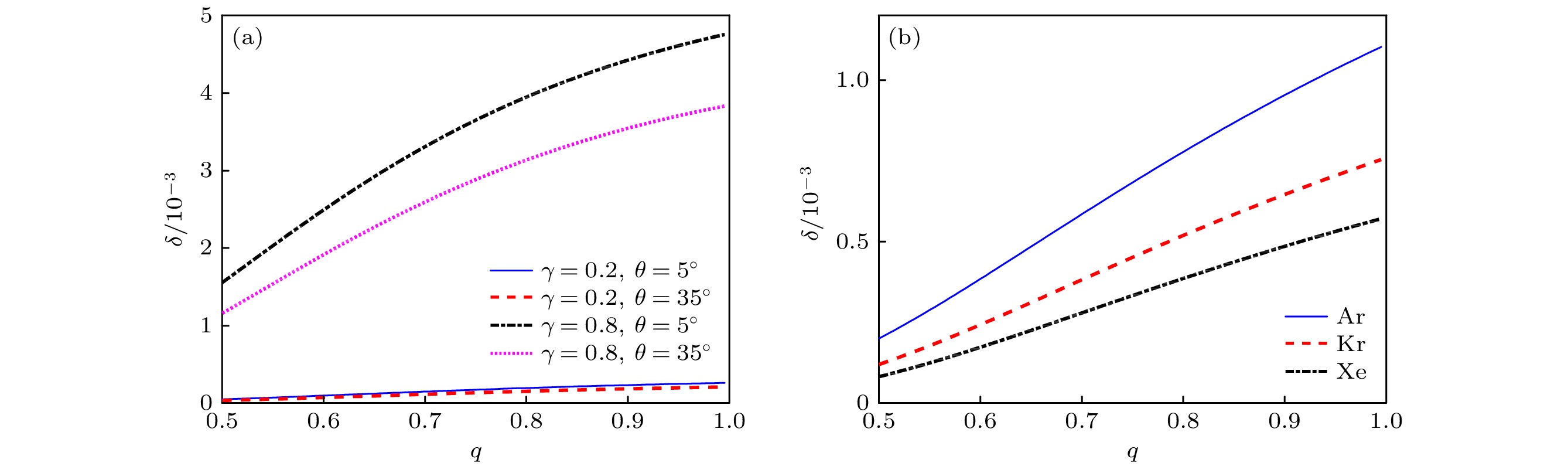
Fig. 4. Wall potential versus non-extensive parameter q: (a) The $ {\varPhi }_{\mathrm{w}}$ for different values of $ \gamma, \theta $; (b) the $ {\varPhi }_{\mathrm{w}}$ for different kinds of plasma.

下载: 全尺寸图片幻灯片

图 5 鞘边二次电子数密度随非广延参数q的变化　(a)不同$ \gamma, \theta $下鞘边二次电子数密度分布; (b)不同等离子体种类下鞘边二次电子数密度分布

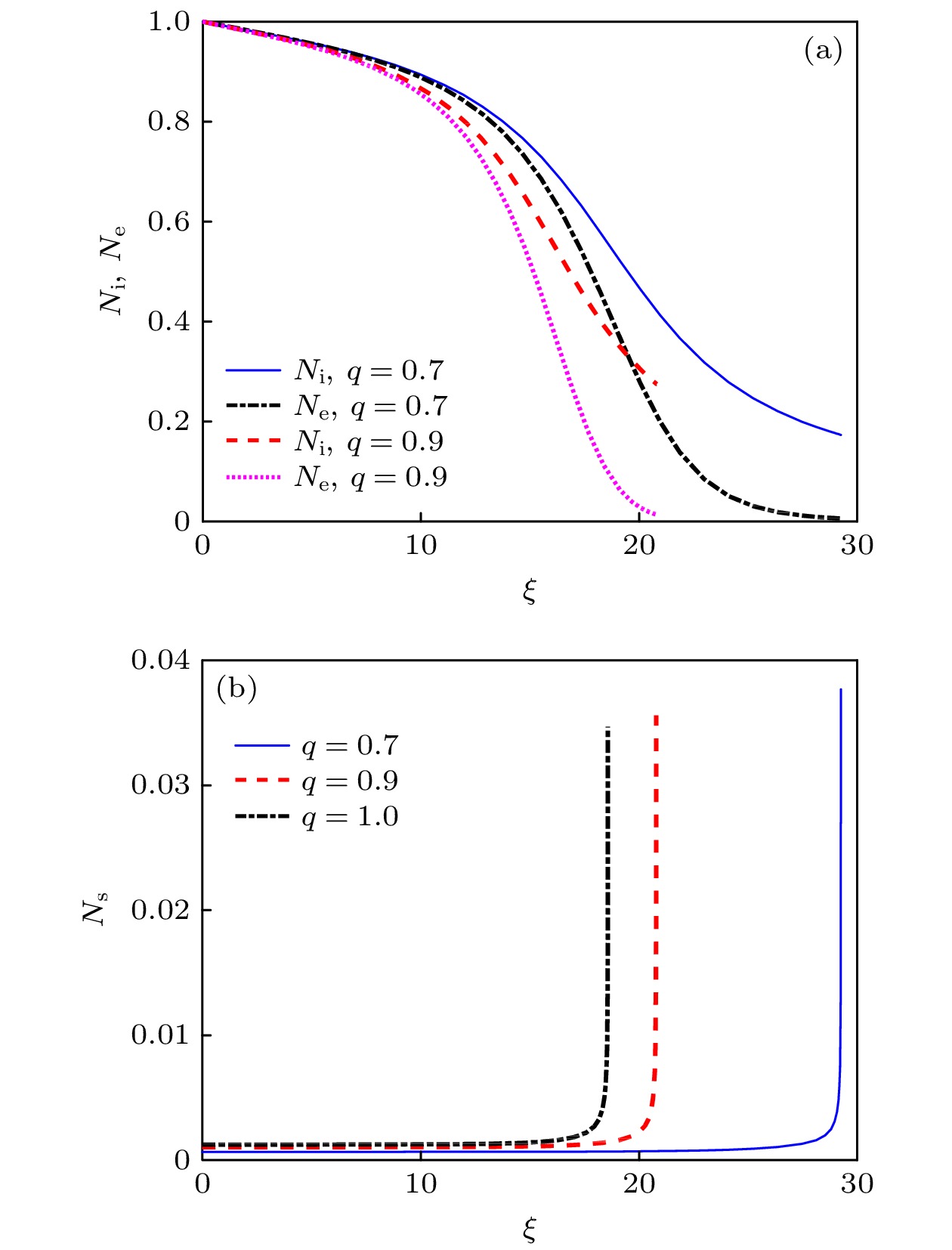
Fig. 5. Normalized density of secondary electrons at the sheath edge versus non-extensive parameter q: (a) Density of secondary electrons at the sheath edge for different values of $ \gamma \; \mathrm{a}\mathrm{n}\mathrm{d} \; \theta $; (b) density of secondary electrons at the sheath edge for different kinds of plasma.

下载: 全尺寸图片幻灯片

图 6 不同非广延参数q值下鞘层电势分布($B=0.04 \; \mathrm{T}, $$ \theta ={20}\text{°},\; \gamma =0.5$)

Fig. 6. Sheath potential distribution with different values of q ($B=0.04 \; \mathrm{T},\; \theta ={20}\text{°},\; \gamma =0.5$).

下载: 全尺寸图片幻灯片

图 7 非广延参数q值及磁场角度对鞘层厚度的影响(B = 0.04 T, $\gamma =0.5$)

Fig. 7. Influence of non-extensive parameter q value and magnetic field angle on sheath thickness ($B=0.04 \; \mathrm{T}, $$ \gamma =0.5$).

下载: 全尺寸图片幻灯片

图 8 非广延参数q值对鞘层粒子数密度分布的影响 ($B=0.04 \; \mathrm{T}, \;\theta ={20}\text{°}, \;\gamma =0.5$)　(a)离子、电子数密度分布; (b)二次电子数密度分布

Fig. 8. Influence of the non-extensive parameter q on the particle number density distribution of the sheath (B = 0.04 T, $ \theta ={20}\text{°},\; \gamma =0.5$): (a) Normalized density of ions and electrons distribution; (b) normalized density of secondary electrons distribution.

下载: 全尺寸图片幻灯片

图 9 磁场对鞘层离子、电子数密度分布的影响($ q=0.8, \gamma =0.5 $)　(a) 磁场大小的影响; (b)磁场角度的影响

Fig. 9. Influence of magnetic field on the number density distribution of sheath ions and electrons ($ q=0.8, \gamma =0.5 $): (a) Variation of normalized particle density for different values of magnetic field strength; (b) variation of normalized particle density for different values of magnetic field angle.

下载: 全尺寸图片幻灯片

图 10 (a)−(c)非广延参数q值和(d)−(f)磁场角度对离子速度的影响($ B=0.04 \; \mathrm{T}, \gamma =0.5 $)　(a) x方向速度($\theta ={20}\text{°}$); (b) y方向速度($\theta ={20}\text{°}$); (c) z方向速度($\theta ={20}\text{°}$); (d) x方向速度, q = 0.5; (e) x方向速度, q = 1; (f) x方向速度, q = 1.5

Fig. 10. Influence of (a)−(c) non-extensive parameter q value and (d)−(f) magnetic field angle on ion velocity ($ B=0.04 \; \mathrm{T}, \gamma =0.5 $): (a) x-component ($\theta ={20}\text{°}$); (b) y-component ($\theta ={20}\text{°}$); (c) z-component ($\theta ={20}\text{°}$); (d) x-component, q = 0.5; (e) x-component, q = 1; (f) x-component, q = 1.5.

下载: 全尺寸图片幻灯片

map

[1]	Franklin R N 2000 J. Phys. D: Appl. Phys. 33 3186 Google Scholar
[2]	Tskhakaya D D, Shukla P K, Eliasson B, Kuhn S 2005 Phys. Plasmas 12 103503 Google Scholar
[3]	Shibata K, Ito H, Yugami N, Miyazaki T, Nishida Y 2001 Thin Solid Films 386 291 Google Scholar
[4]	Hatami M M 2015 Phys. Plasmas 22 023506 Google Scholar
[5]	Aanesland A, Rafalskyi D, Bredin J, Grondein P, Oudini N, Chabert P, Levko D, Garrigues L, Hagelaar G 2015 IEEE Trans. Plasma Sci. 43 321 Google Scholar
[6]	Adhikari S, Moulick R, Goswami K S 2017 Phys. Plasmas 224 083501 Google Scholar
[7]	Liu J Y, Zhang Q, Zou X, Wang Z X, Liu Y, Wang X G, Gong Y 2004 Vacuum 73 687 Google Scholar
[8]	Driouch I, Chatei H, Bojaddaini M E 2015 Phys. Plasmas 81 905810104 Google Scholar
[9]	Benlemdjaldi D, Tahraoui A, Hugon R, Bougdira J 2013 Phys. Plasmas 20 043508 Google Scholar
[10]	王正汹, 刘金远, 邹秀, 刘悦, 王晓刚 2004 53 793 Google Scholar Wang Z X, Liu J Y, Zou X, Liu Y, Wang X G 2004 Acta Phys. Sin. 53 793 Google Scholar
[11]	Saslaw W C, Arp H 1986 Phys. Today 39 61 Google Scholar
[12]	Cáceres M O 1999 Braz. J. Phys. 29 125 Google Scholar
[13]	Tsallis C, Mendes R, Plastino A R 1998 Physica A 261 534 Google Scholar
[14]	Hatami M M, Tribeche M 2018 IEEE Trans. Plasma Sci. 46 868 Google Scholar
[15]	Meige A, Boswell R W 2006 Phys. Plasmas 13 92104 Google Scholar
[16]	Singh H, Graves D B 2000 J. Appl. Phys. 88 3889 Google Scholar
[17]	Tsallis C 1988 J. Stat. Phys. 52 479 Google Scholar
[18]	Borgohain D R, Saharia K, Goswami K S 2016 Phys. Plasmas 23 122113 Google Scholar
[19]	Driouch I, Chatei H 2017 Eur. Phys. J. D. 71 1 Google Scholar
[20]	Hatami M M, Tribeche M, Mamun A A 2018 Phys. Plasmas 25 094502 Google Scholar
[21]	Hatami M M, Tribeche M, Mamun A A 2019 Astrophysics Space Sci. 364 1 Google Scholar
[22]	Zhao X Y, Zhang B K, Wang C X 2020 Phys. Plasmas 27 113705 Google Scholar
[23]	Safa N N, Ghomi H, Niknam A R 2014 Phys. Plasmas 21 082111 Google Scholar
[24]	Basnet S, Khanal R 2019 Phys. Plasmas 26 043516 Google Scholar
[25]	Zou X, Liu H P, Zhu Y Z, Zang X N, Qiu M H 2020 Plasmas Sci. Technol. 22 125001 Google Scholar
[26]	Dhawan R, Kumar M, Malik H K 2020 Phys. Plasmas 27 063515 Google Scholar
[27]	Basnet S, Patel A, Khanal R 2020 Plasma Phys. Control. Fusion 62 115011 Google Scholar
[28]	赵晓云, 张丙开, 王春晓, 唐义甲 2019 68 185204 Google Scholar Zhao X Y, Zhang B K, Wang C X, Tang Y J 2019 Acta Phys. Sin. 68 185204 Google Scholar
[29]	Ghani O E, Driouch I, Chatei H 2020 Phys. Plasmas 27 083701 Google Scholar
[30]	邹秀, 刘惠平, 张小楠, 邱明辉 2021 70 015201 Google Scholar Zou X, Liu H P, Zhang X N, Qiu M H 2021 Acta Phys. Sin. 70 015201 Google Scholar
[31]	Dhawan R, Malik H K 2021 Plasmas Sci. Technol. 23 045402 Google Scholar
[32]	Bezerra J R, Silva R, Lima J A S 2003 Physica A 322 256 Google Scholar
[33]	Safa N N, Ghomi H, Niknam A R 2015 Phys. Plasmas 81 905810303 Google Scholar
[34]	Borgohain D R, Saharia K 2018 Phys. Plasmas 25 032122 Google Scholar
[35]	Tribeche M, Djebarni L, Amour R 2010 Phys. Plasmas 17 042114 Google Scholar
[36]	Hatami M M 2015 Phys. Plasmas 22 013508 Google Scholar
[37]	Chen F F 1974 Introduction to Plasma Physics (New York: Springer Science)

[1]	胡笑钏, 刘样溪, 楚坤, 段潮锋. 非晶态碳薄膜对金属二次电子发射的影响. , 2024, 73(4): 047901. doi: 10.7498/aps.73.20231604
[2]	陈龙, 檀聪琦, 崔作君, 段萍, 安宇豪, 陈俊宇, 周丽娜. 电子非广延分布的多离子磁化等离子体鞘层特性. , 2024, 73(5): 055201. doi: 10.7498/aps.73.20231452
[3]	孟祥琛, 王丹, 蔡亚辉, 叶振, 贺永宁, 徐亚男. 氧化铝表面二次电子发射抑制及其在微放电抑制中的应用. , 2023, 72(10): 107901. doi: 10.7498/aps.72.20222404
[4]	李涵汐, 王德真. 热电子发射对钨偏滤器靶板附近磁化鞘层影响的模拟研究. , 2023, 72(15): 159401. doi: 10.7498/aps.72.20230276
[5]	张含天, 周前红, 周海京, 孙强, 宋萌萌, 董烨, 杨薇, 姚建生. 二次电子发射对系统电磁脉冲的影响. , 2021, 70(16): 165201. doi: 10.7498/aps.70.20210461
[6]	邹秀, 刘惠平, 张小楠, 邱明辉. 具有非广延分布电子的碰撞等离子体磁鞘的结构. , 2021, 70(1): 015201. doi: 10.7498/aps.70.20200794
[7]	刘惠平, 邹秀. 电子和负离子的反射运动对碰撞电负性磁鞘的影响. , 2020, 69(2): 025201. doi: 10.7498/aps.69.20191307
[8]	王丹, 叶鸣, 冯鹏, 贺永宁, 崔万照. 激光刻蚀对镀金表面二次电子发射的有效抑制. , 2019, 68(6): 067901. doi: 10.7498/aps.68.20181547
[9]	赵晓云, 张丙开, 王春晓, 唐义甲. 电子的非广延分布对等离子体鞘层中二次电子发射的影响. , 2019, 68(18): 185204. doi: 10.7498/aps.68.20190225
[10]	胡晶, 曹猛, 李永东, 林舒, 夏宁. 微米量级表面结构形貌特性对二次电子发射抑制的优化. , 2018, 67(17): 177901. doi: 10.7498/aps.67.20180466
[11]	白春江, 封国宝, 崔万照, 贺永宁, 张雯, 胡少光, 叶鸣, 胡天存, 黄光荪, 王琪. 铝阳极氧化的多孔结构抑制二次电子发射的研究. , 2018, 67(3): 037902. doi: 10.7498/aps.67.20172243
[12]	张娜, 曹猛, 崔万照, 胡天存, 王瑞, 李韵. 金属规则表面形貌影响二次电子产额的解析模型. , 2015, 64(20): 207901. doi: 10.7498/aps.64.207901
[13]	李永东, 杨文晋, 张娜, 崔万照, 刘纯亮. 一种二次电子发射的复合唯象模型. , 2013, 62(7): 077901. doi: 10.7498/aps.62.077901
[14]	杨文晋, 李永东, 刘纯亮. 高入射能量下的金属二次电子发射模型. , 2013, 62(8): 087901. doi: 10.7498/aps.62.087901
[15]	赵晓云, 张丙开, 张开银. 两种带电尘埃颗粒的等离子体鞘层玻姆判据. , 2013, 62(17): 175201. doi: 10.7498/aps.62.175201
[16]	邱明辉, 刘惠平, 邹秀. 斜磁场作用下碰撞电负性等离子体鞘层的玻姆判据. , 2012, 61(15): 155204. doi: 10.7498/aps.61.155204
[17]	刘惠平, 邹秀, 邹滨雁, 邱明辉. 电负性等离子体磁鞘的玻姆判据. , 2012, 61(3): 035201. doi: 10.7498/aps.61.035201
[18]	赵晓云, 刘金远, 段萍, 倪致祥. 不同成分等离子体鞘层的玻姆判据. , 2011, 60(4): 045205. doi: 10.7498/aps.60.045205
[19]	邹秀, 籍延坤, 邹滨雁. 斜磁场中碰撞等离子体鞘层的玻姆判据. , 2010, 59(3): 1902-1906. doi: 10.7498/aps.59.1902
[20]	王正汹, 刘金远, 邹　秀, 刘　悦, 王晓钢. 尘埃等离子体鞘层的玻姆判据. , 2004, 53(3): 793-797. doi: 10.7498/aps.53.793

计量

文章访问数: 4088
PDF下载量: 75
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

电子非麦氏分布的二次电子发射磁化鞘层特性