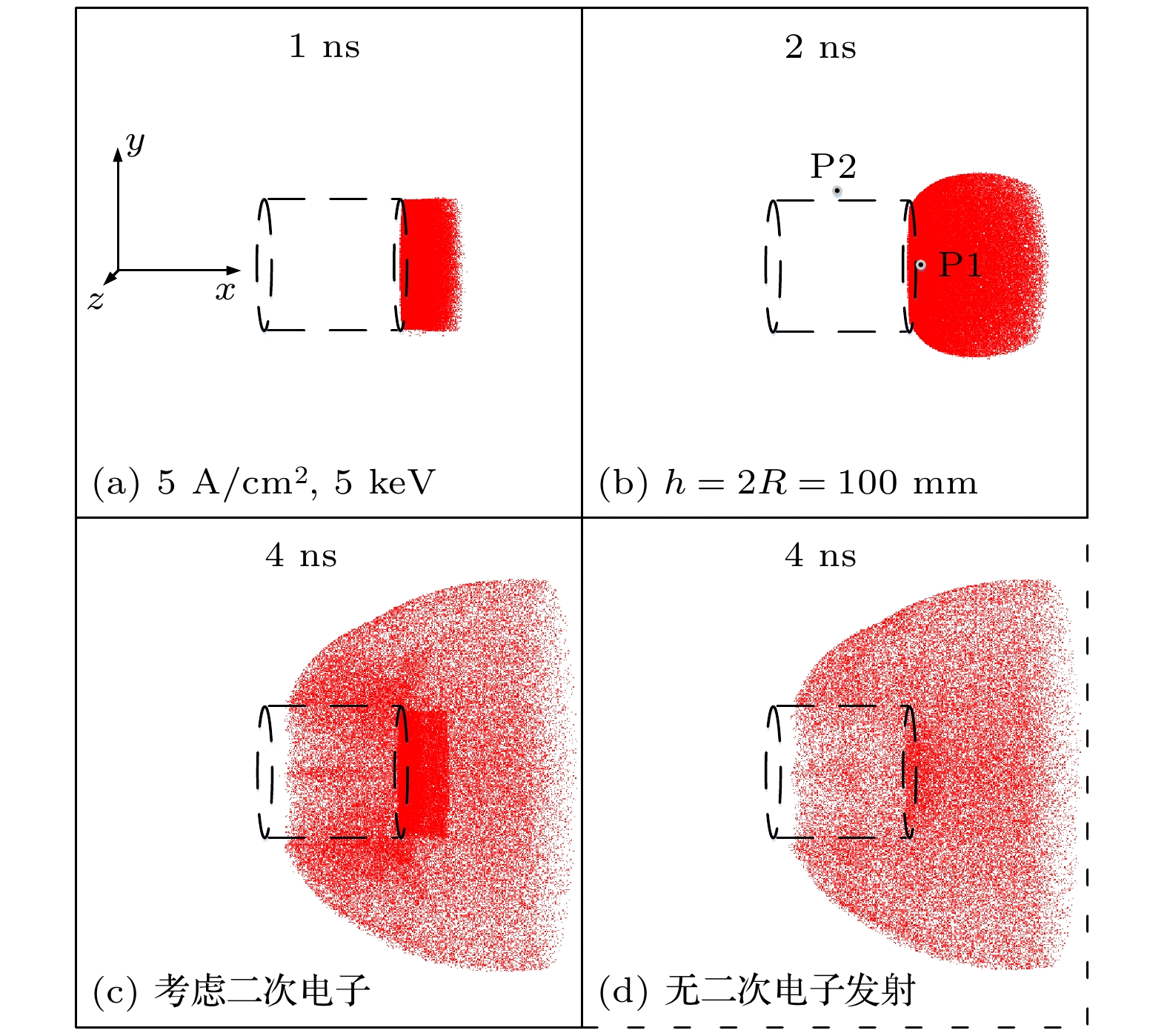
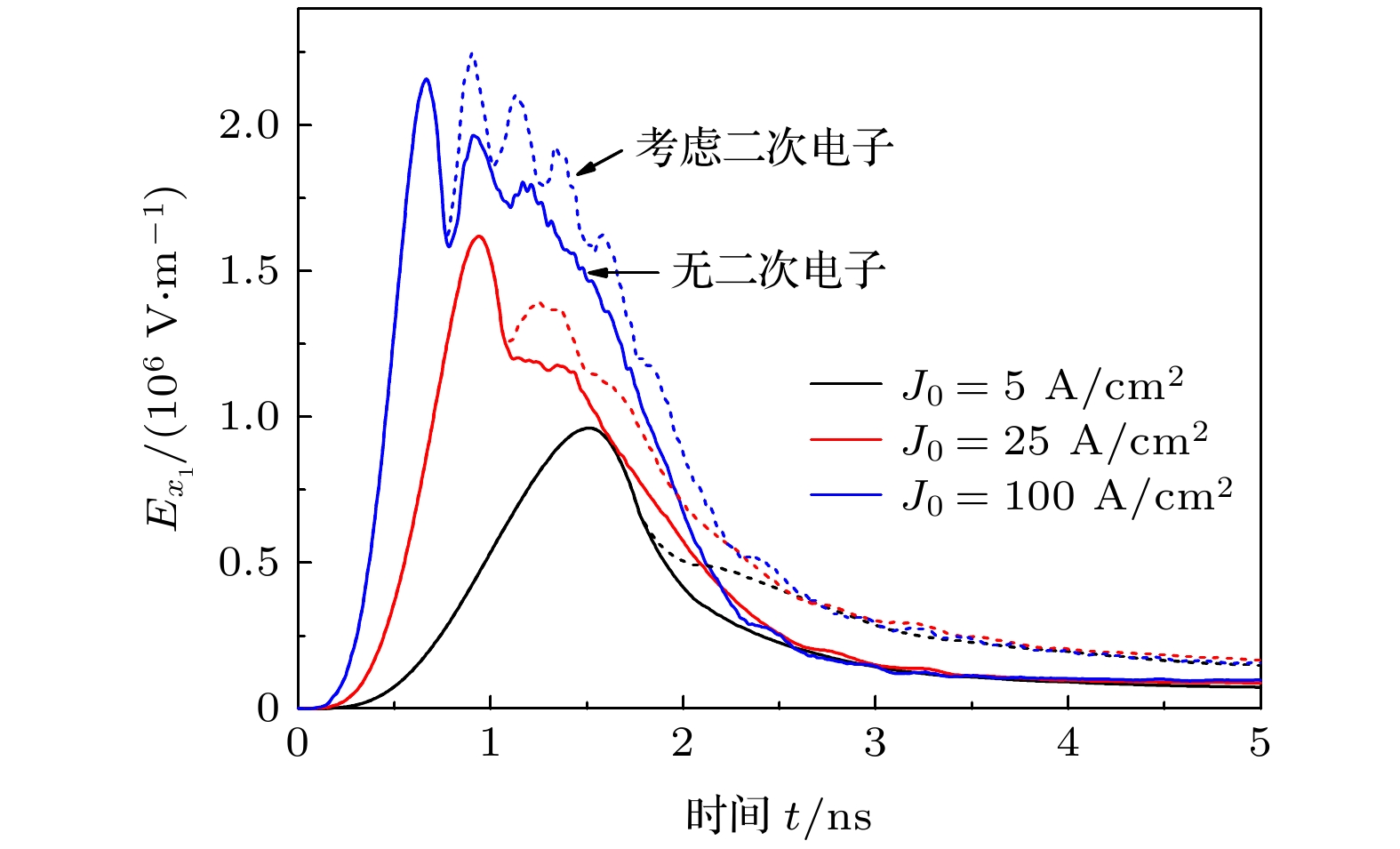
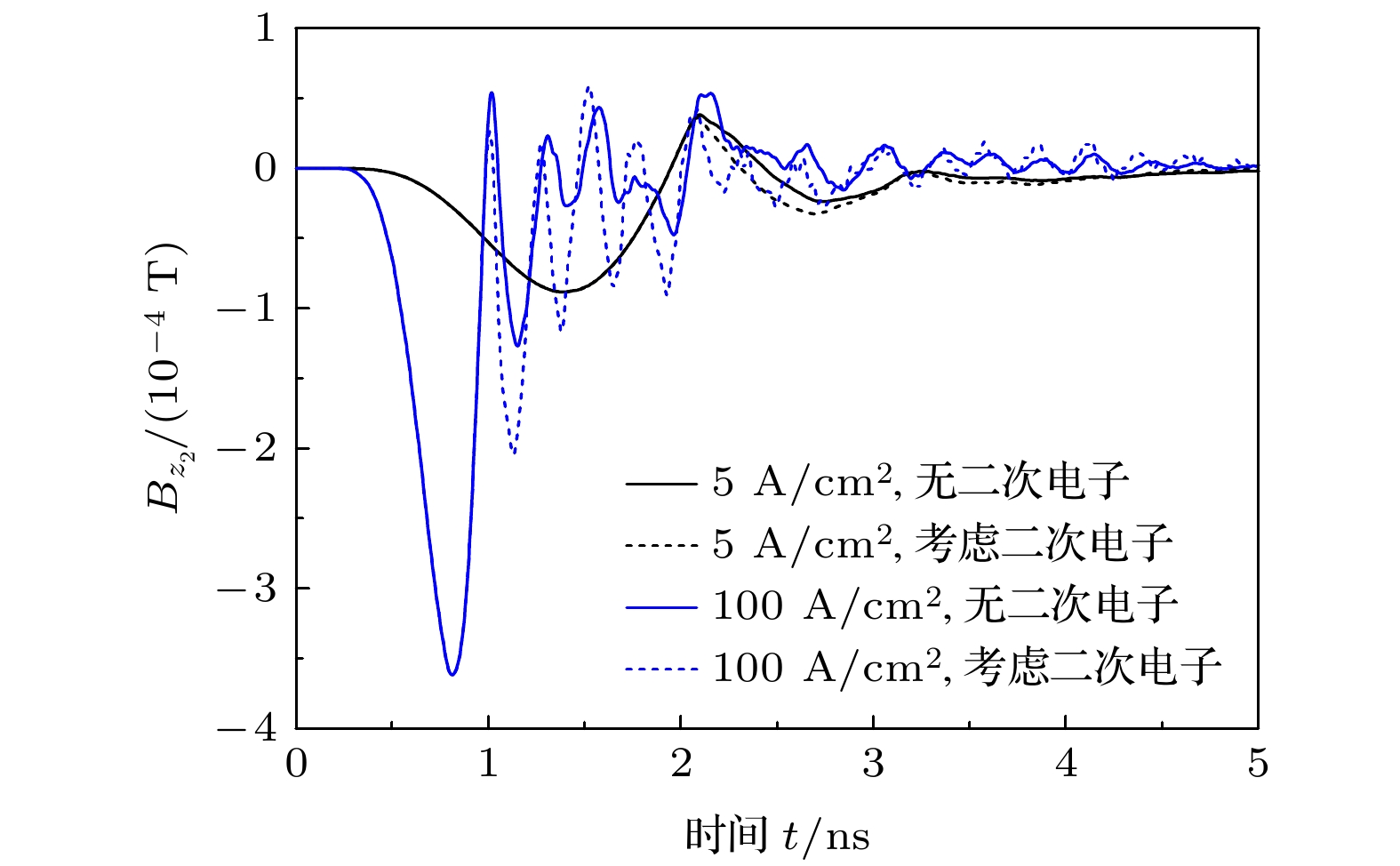
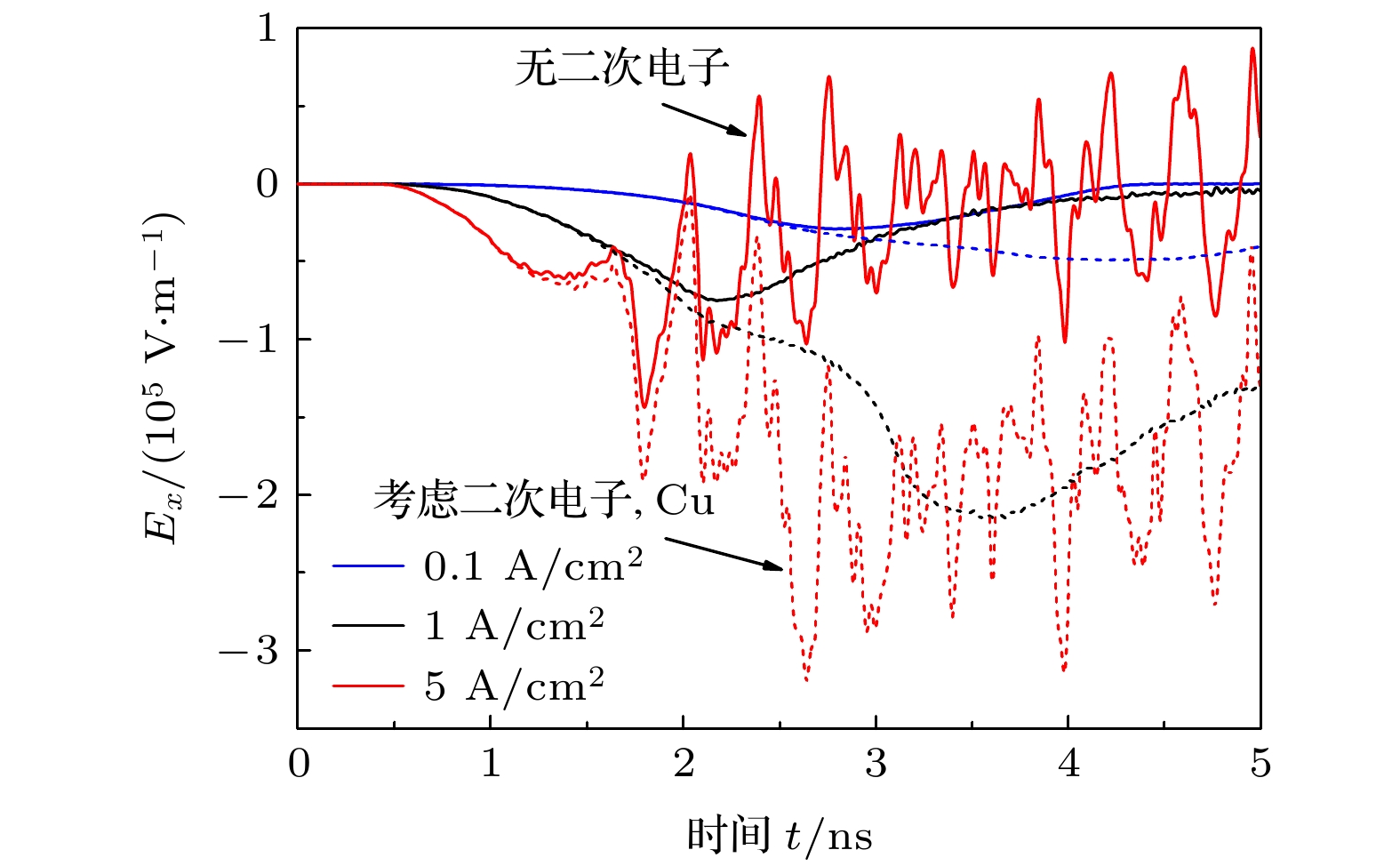
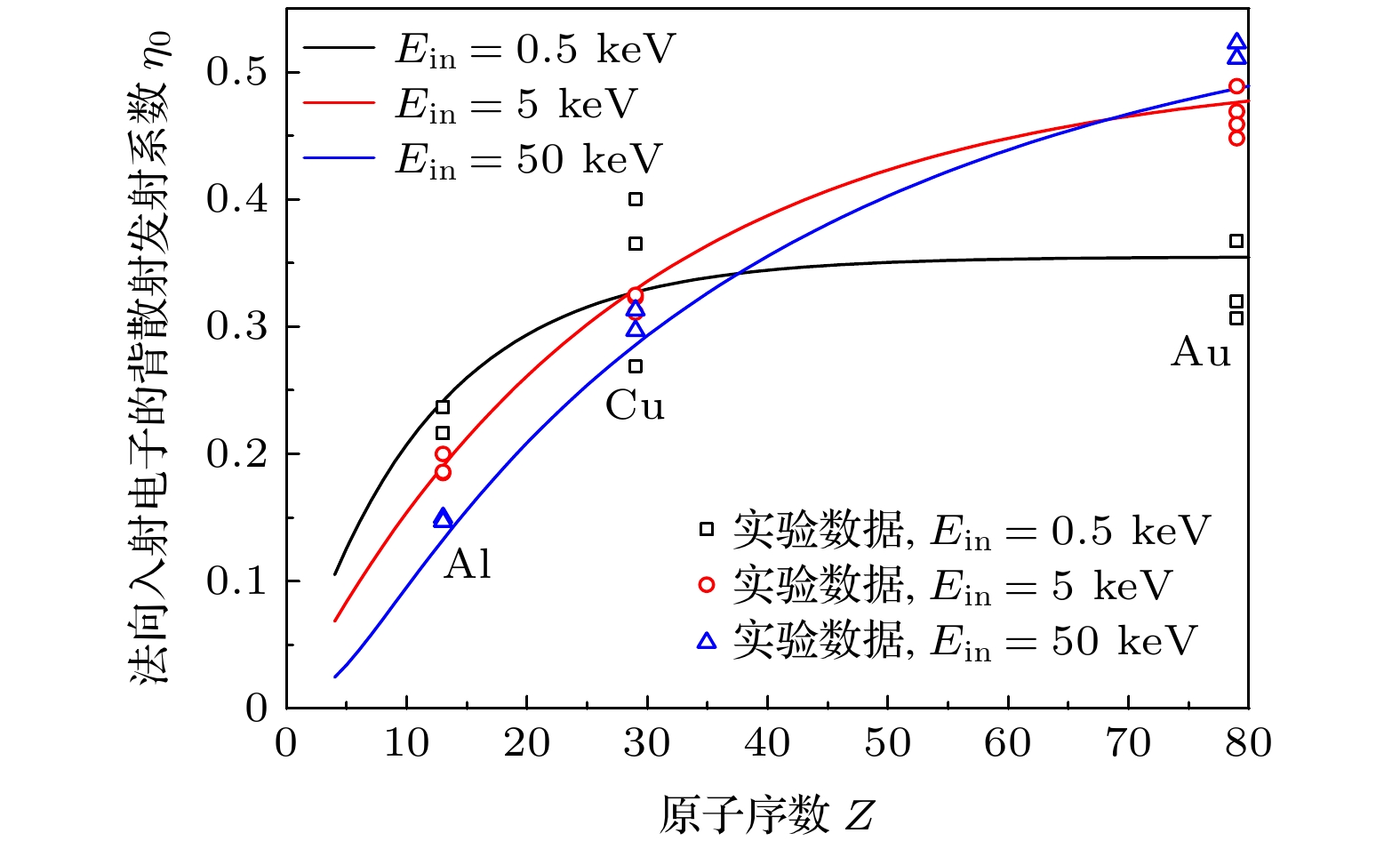
-
系统电磁脉冲难以有效屏蔽, 会显著影响低轨航天器等重要装置和基础设施的性能. 为了评估二次电子对系统电磁脉冲的影响, 本文基于粒子云网格方法, 建立了三维非稳态系统电磁脉冲模型, 计算并比较了不同电流密度、金属材料等条件下, 两种典型结构的电磁脉冲响应. 结果表明, 在计算模型中忽略二次电子发射会使部分位置的峰值电场强度被低估2—3倍, 电场响应持续的时间也会被低估10%以上. 在各类二次电子中, 背散射电子对系统电磁脉冲的影响占主导, 而真二次电子的作用约为背散射电子的1/5. 二次电子发射对系统电磁脉冲的影响随着系统所用材料原子序数的增高而加大. 空间电荷效应较强时, 二次电子才会对腔体外系统电磁脉冲产生影响. 本研究有助于更好地通过数值模拟来获得具体装置在强辐射环境下的系统电磁脉冲响应.It is difficult to effectively shield the system generated electromagnetic pulse (SGEMP), which can significantly affect the performance of important electronic devices and infrastructure, such as low-orbit spacecraft. Numerical simulation is an essential way to study the SGEMP response. However, many previous studies ignored or simplified the effect of secondary electron emission in their models. In this paper, a three-dimensional electromagnetic particle-in-cell numerical simulation model is developed to evaluate the effect of secondary electrons on the SGEMP response of two typical structures (external SGEMP and cavity SGEMP, respectively) under different current densities (0.1–100 A/cm2) and different materials (Al, Cu and Au). A right cylinder or cylindrical cavity with a length of 100 mm is used. The photoelectrons produced by the interaction between the X-ray photon and metal are emitted from one end of the system and assumed to be monoenergetic. The photoelectron pulse follows a sine-squared distribution, and its full width at half maximum is 1 ns. Some important parameters of secondary electrons are discussed and summarized, including the emission coefficients of elastically and inelastically backscattered electrons, as well as the probability density functions of emission angles and energies. The results show that ignoring the secondary emission in the simulation model leads the peak electric field to be underestimated by twice-thrice, and the duration of electric field response by more than 10%. The oscillation frequency and the amplitude of the second peak of the tangential magnetic field are also increased, with the secondary electrons considered. Among various types of secondary electrons, backscattered electrons have a dominant effect on the change of SGEMP. The effect of true secondary electrons is about 1/5 of that of backscattered electrons. The effect of secondary electrons on SGEMP response increases with a higher atomic number of the material used in the system, mainly due to higher backscattering emission coefficient and a high ratio of high energy inelastically backscattered electrons. The secondary electrons will influence the response of the external SGEMP only when the space charge effect is strong (high X-ray fluence). While the response of the cavity SGEMP is more easily affected by the secondary electrons even at a relatively low X-ray fluence. This paper helps to better obtain the SGEMP response of a specific device under strong radiation through numerical simulation.
-
Keywords:
- secondary electrons /
- system generated electromagnetic pulse /
- photoelectrons /
- particle-in-cell simulation
[1] 王泰春, 贺云汉, 王玉芝 2011 电磁脉冲导论 (北京: 国防工业出版社) 第130页
Wang T C, He Y H, Wang Y Z 2011 Introduction to Electromagnetic Pulse (Beijing: National Defense Industry Press) p130 (in Chinese)
[2] 美国电磁脉冲袭击对美威胁评估委员会编 (郑毅, 梁睿, 曹保锋 译 2019 电磁脉冲袭击对国家重要基础设施的影响 (北京: 科学出版社) 第9页
Commission to assess the threat to the United States from electromagnetic pulse (EMP) attack (translated by Zheng Y, Liang R, Cao B F) 2019 Report of the Commission to Assess the Threat to the United States from Electromagnetic Pulse (EMP) Attack: Critical National Infrastructures (Beijing: Science Press) p9
[3] Gilbert R M, Klebers J, Bromborsky A 1977 IEEE Trans. Nucl. Sci. 24 2389
Google Scholar
[4] Genuario R D 1975 IEEE Trans. Nucl. Sci. 22 2098
Google Scholar
[5] Woods A J, Wenaas E P 1976 IEEE Trans. Nucl. Sci. 23 1903
Google Scholar
[6] Woods A J, Hobbs W E, Wenaas E P 1981 IEEE Trans. Nucl. Sci. 28 4467
Google Scholar
[7] Chan P C, Woods A J 1985 IEEE Trans. Nucl. Sci. 32 4441
Google Scholar
[8] 王泰春, 王玉芝 1986 计算物理 3 86
Wang T C, Wang Y Z 1986 Chinese J. Comput. Phys. 3 86
[9] Li J X, Cheng Y H, Wu W, Zhou H 2008 Proceedings of the 14th National Annual Conference on Nuclear Electronics and Nuclear Detection Technology Urumqi, China, July 15−20, 2008 p735
[10] Holland R 1995 IEEE Trans. Electromagn. Compat. 37 433
Google Scholar
[11] Pointon T D, Cartwright K L 2014 Proceedings of the 67th APS Gaseous Electronics Conference Raleigh NC, USA, November 2−7, 2014 p00051
[12] Angus J R, Mosher D, Swanekamp S B, Ottinger P F, Schumer J W, Hinshelwood D D 2016 Phys. Plasmas 23 053510
Google Scholar
[13] 孙会芳, 张芳, 董志伟 2016 计算物理 33 434
Google Scholar
Sun H F, Zhang F, Dong Z W 2016 Chinese J. Comput. Phys. 33 434
Google Scholar
[14] Chen J N, Wang J G, Chen Z G, Ren Z P 2020 IEEE Trans. Nucl. Sci. 67 818
Google Scholar
[15] Chen J H, Chao Z, Deng J H, Li Z D Z 2020 IEEE Trans. Nucl. Sci. 67 2353
Google Scholar
[16] Meng C, Xu Z Q, Jiang Y S, Zheng W G, Dang Z 2017 IEEE Trans. Nucl. Sci. 64 2618
Google Scholar
[17] Xu Z Q, Meng C, Jiang Y S, Wu P 2020 IEEE Trans. Nucl. Sci. 67 425
Google Scholar
[18] Wenaas E P, Woods A J 1976 IEEE Trans. Nucl. Sci. 23 1921
Google Scholar
[19] 周俊 2009 博士学位论文(成都: 电子科技大学)
Zhou J 2009 Ph. D. Dissertation (Chengdu: University of Electronic Science and Technology of China) (in Chinese)
[20] Reimer L 2000 Scanning Electron Microscopy: Physics of Image Formation and Microanalysis (New York: Springer) p4
[21] 谢爱根, 裴元吉, 王荣, 孙红兵 2005 高能物理与核物理 5 530
Xie A G, Pei Y J, Wang R, Sun H B 2005 High Energy Phys. Nuclear Phys. 5 530
[22] Vaughan J R M 1989 IEEE Trans. Electron Devices 36 1963
Google Scholar
[23] Valfells Á, Singh A, Kolander M J, Granatstein V L 2002 IEEE Trans. Plasma Sci. 30 1271
Google Scholar
[24] Furman M A, Pivi M T F 2002 Phys. Rev. Spec. Top. - Accel. Beams 5 124404
Google Scholar
[25] Sternglass E J 1954 Phys. Rev. 95 345
Google Scholar
[26] Joy D C 1995 Scanning 17 270
Google Scholar
[27] Hussain A, Yang L H, Mao S F, Da B, Tőkési K, Ding Z H 2021 Nucl. Mater. Energy 26 100862
Google Scholar
[28] 刘腊群, 刘大刚, 王学琼, 彭凯, 杨超 2012 强激光与粒子束 24 1980
Google Scholar
Liu L Q, Liu D G, Wang X Q, Peng K, Yang C 2012 High Power Laser and Particle Beams 24 1980
Google Scholar
[29] Staub P F 1994 J. Phys. D Appl. Phys. 27 1533
Google Scholar
[30] Matsukawa T, Shimizu R, Hashimoto H 1974 J. Phys. D Appl. Phys. 7 695
Google Scholar
[31] 陈剑楠, 陶应龙, 陈再高, 王玥 2018 现代应用物理 9 040501
Google Scholar
Chen J N, Tao Y L, Chen Z G, Wang Y 2018 Modern Appl. Phys. 9 040501
Google Scholar
[32] 郭景海, 周辉, 吴伟, 程引会, 李进玺, 马良, 赵墨 2016 核电子学与探测技术 36 512
Google Scholar
Guo J H, Zhou H, Wu W, Cheng Y H, Li J X, Ma L, Zhao M 2016 Nuclear Electronics and Detection Techol. 36 512
Google Scholar
-
图 2 计算模型示意图 (a)腔体外SGEMP; (b)腔体内SGEMP
Fig. 2. Schematics of the calculation domain: (a) The external SGEMP; (b) the internal SGEMP.
图 3 不同时刻电子的空间分布(J0 = 5 A/cm2, E0 = 5 keV). (a)(b)(c)考虑二次电子发射; (d)无二次电子发射的情况
Fig. 3. Distribution of electrons at different moments on the condition J0 = 5 A/cm2 and E0 = 5 keV: (a)(b)(c)Including secondary emission; (d)without secondary electrons.
图 4 不同峰值电流密度条件下, P1位置的轴向电场强度Ex (实线: 未考虑二次电子发射, 虚线: 考虑二次电子发射, E0 = 5 keV)
Fig. 4. Axial electric field Ex at P1 for different peak current densities (Solid line: not including secondary electrons; dash line: including secondary electrons, E0 = 5 keV).
图 5 不同峰值电流密度条件下, P2位置的径向电场强度Ey (实线: 未考虑二次电子发射, 虚线: 考虑二次电子发射, 点线: 仅考虑背散射电子, E0 = 5 keV)
Fig. 5. Radial electric field Ey at P2 for different peak current densities (Solid line: not including secondary electrons; dash line: including secondary electrons; dot line: only considering backscattering electrons, E0 = 5 keV).
图 6 在J0 = 5, 100 A/cm2条件下, P2位置的磁感应强度BZ (实线: 未考虑二次电子发射, 虚线: 考虑二次电子发射, E0 = 5 keV)
Fig. 6. Magnetic field BZ at P2 for J0 = 5, 100 A/cm2 (Solid line: not including secondary electrons; dash line: including secondary electrons, E0 = 5 keV)
图 7 不同腔体材料, P1位置的轴向电场强度Ex(J0 = 1 A/cm2, E0 = 5 keV)
Fig. 7. Axial electric field Ex at P1 for different materials (J0 = 1 A/cm2, E0 = 5 keV).
图 8 不同位置(P1, P2, P3)的轴向电场强度Ex (J0 = 1 A/cm2, E0 = 5 keV)
Fig. 8. Axial electric field Ex at P1, P2 and P3 (J0 = 1 A/cm2, E0 = 5 keV).
图 9 不同峰值电流密度下, P1位置的轴向电场强度Ex (实线: 未考虑二次电子发射, 虚线: 考虑二次电子发射, E0 = 5 keV)
Fig. 9. Axial electric field Ex at P1 for different peak current densities (Solid line: not including secondary electrons; dash line: including secondary electrons, E0 = 5 keV).
图 10 E0 = 5 keV与E0 = 50 keV条件下, P1位置的轴向电场强度Ex(J0 = 1 A/cm2)
Fig. 10. Axial electric field Ex at P1 for E0 = 5 keV and E0 = 50 keV (J0 = 1 A/cm2).
-
[1] 王泰春, 贺云汉, 王玉芝 2011 电磁脉冲导论 (北京: 国防工业出版社) 第130页
Wang T C, He Y H, Wang Y Z 2011 Introduction to Electromagnetic Pulse (Beijing: National Defense Industry Press) p130 (in Chinese)
[2] 美国电磁脉冲袭击对美威胁评估委员会编 (郑毅, 梁睿, 曹保锋 译 2019 电磁脉冲袭击对国家重要基础设施的影响 (北京: 科学出版社) 第9页
Commission to assess the threat to the United States from electromagnetic pulse (EMP) attack (translated by Zheng Y, Liang R, Cao B F) 2019 Report of the Commission to Assess the Threat to the United States from Electromagnetic Pulse (EMP) Attack: Critical National Infrastructures (Beijing: Science Press) p9
[3] Gilbert R M, Klebers J, Bromborsky A 1977 IEEE Trans. Nucl. Sci. 24 2389
Google Scholar
[4] Genuario R D 1975 IEEE Trans. Nucl. Sci. 22 2098
Google Scholar
[5] Woods A J, Wenaas E P 1976 IEEE Trans. Nucl. Sci. 23 1903
Google Scholar
[6] Woods A J, Hobbs W E, Wenaas E P 1981 IEEE Trans. Nucl. Sci. 28 4467
Google Scholar
[7] Chan P C, Woods A J 1985 IEEE Trans. Nucl. Sci. 32 4441
Google Scholar
[8] 王泰春, 王玉芝 1986 计算物理 3 86
Wang T C, Wang Y Z 1986 Chinese J. Comput. Phys. 3 86
[9] Li J X, Cheng Y H, Wu W, Zhou H 2008 Proceedings of the 14th National Annual Conference on Nuclear Electronics and Nuclear Detection Technology Urumqi, China, July 15−20, 2008 p735
[10] Holland R 1995 IEEE Trans. Electromagn. Compat. 37 433
Google Scholar
[11] Pointon T D, Cartwright K L 2014 Proceedings of the 67th APS Gaseous Electronics Conference Raleigh NC, USA, November 2−7, 2014 p00051
[12] Angus J R, Mosher D, Swanekamp S B, Ottinger P F, Schumer J W, Hinshelwood D D 2016 Phys. Plasmas 23 053510
Google Scholar
[13] 孙会芳, 张芳, 董志伟 2016 计算物理 33 434
Google Scholar
Sun H F, Zhang F, Dong Z W 2016 Chinese J. Comput. Phys. 33 434
Google Scholar
[14] Chen J N, Wang J G, Chen Z G, Ren Z P 2020 IEEE Trans. Nucl. Sci. 67 818
Google Scholar
[15] Chen J H, Chao Z, Deng J H, Li Z D Z 2020 IEEE Trans. Nucl. Sci. 67 2353
Google Scholar
[16] Meng C, Xu Z Q, Jiang Y S, Zheng W G, Dang Z 2017 IEEE Trans. Nucl. Sci. 64 2618
Google Scholar
[17] Xu Z Q, Meng C, Jiang Y S, Wu P 2020 IEEE Trans. Nucl. Sci. 67 425
Google Scholar
[18] Wenaas E P, Woods A J 1976 IEEE Trans. Nucl. Sci. 23 1921
Google Scholar
[19] 周俊 2009 博士学位论文(成都: 电子科技大学)
Zhou J 2009 Ph. D. Dissertation (Chengdu: University of Electronic Science and Technology of China) (in Chinese)
[20] Reimer L 2000 Scanning Electron Microscopy: Physics of Image Formation and Microanalysis (New York: Springer) p4
[21] 谢爱根, 裴元吉, 王荣, 孙红兵 2005 高能物理与核物理 5 530
Xie A G, Pei Y J, Wang R, Sun H B 2005 High Energy Phys. Nuclear Phys. 5 530
[22] Vaughan J R M 1989 IEEE Trans. Electron Devices 36 1963
Google Scholar
[23] Valfells Á, Singh A, Kolander M J, Granatstein V L 2002 IEEE Trans. Plasma Sci. 30 1271
Google Scholar
[24] Furman M A, Pivi M T F 2002 Phys. Rev. Spec. Top. - Accel. Beams 5 124404
Google Scholar
[25] Sternglass E J 1954 Phys. Rev. 95 345
Google Scholar
[26] Joy D C 1995 Scanning 17 270
Google Scholar
[27] Hussain A, Yang L H, Mao S F, Da B, Tőkési K, Ding Z H 2021 Nucl. Mater. Energy 26 100862
Google Scholar
[28] 刘腊群, 刘大刚, 王学琼, 彭凯, 杨超 2012 强激光与粒子束 24 1980
Google Scholar
Liu L Q, Liu D G, Wang X Q, Peng K, Yang C 2012 High Power Laser and Particle Beams 24 1980
Google Scholar
[29] Staub P F 1994 J. Phys. D Appl. Phys. 27 1533
Google Scholar
[30] Matsukawa T, Shimizu R, Hashimoto H 1974 J. Phys. D Appl. Phys. 7 695
Google Scholar
[31] 陈剑楠, 陶应龙, 陈再高, 王玥 2018 现代应用物理 9 040501
Google Scholar
Chen J N, Tao Y L, Chen Z G, Wang Y 2018 Modern Appl. Phys. 9 040501
Google Scholar
[32] 郭景海, 周辉, 吴伟, 程引会, 李进玺, 马良, 赵墨 2016 核电子学与探测技术 36 512
Google Scholar
Guo J H, Zhou H, Wu W, Cheng Y H, Li J X, Ma L, Zhao M 2016 Nuclear Electronics and Detection Techol. 36 512
Google Scholar
下载:
计量
- 文章访问数: 4997
- PDF下载量: 93
- 被引次数: 0
