-
相干布居振荡(coherent population oscillations, CPO)光谱是一种原子布居数调制光谱, 主要利用两束位相锁定、频率差小于原子自发辐射线宽的耦合光和探测光与原子相互作用, 激光强度调制会导致原子布居数相干振荡, 实现窄带宽的探测光透射. 本文基于Λ型原子能级结构, 在室温铯原子系综中实现了相干布居振荡光谱, 光谱典型线宽小于50 kHz, 远低于5.2 MHz的自发辐射线宽. Λ型能级结构的相干布居振荡光谱线宽依赖多个简并能级系统的布居数关联振荡, 其不要求原子态的相位关联, 有利于在长激发态寿命的Rydberg原子系统中基于相干布居振荡获得窄线宽光谱, 从而提高基于Rydberg原子光谱的精密测量的灵敏度.Coherent population oscillations spectroscopy, which is based on the interaction between atoms and the phase locked laser, is a kind of atomic population modulation spectroscopy. When the laser frequency difference is less than natural width of energy level, the coherent oscillation of atomic population will be induced by laser intensity modulation so that the probe laser transmission with narrow bandwidth can be realized. For a closed two-level system (TLS), the spectral line-width is limited mainly by the spontaneous emission lifetime of the upper atomic energy level. As for a three-level atomic system of Λ configuration, the two linearly polarized beams with both σ+ and σ- polarization component, the laser-atom interaction satisfies the selection rule. The spectral line-width mainly depends on the ground-state relaxation time, and the dependence on the line-width of spontaneous radiation is eliminated. In this paper, the laser from a external-cavity diode laser has its frequency locked to Cesium
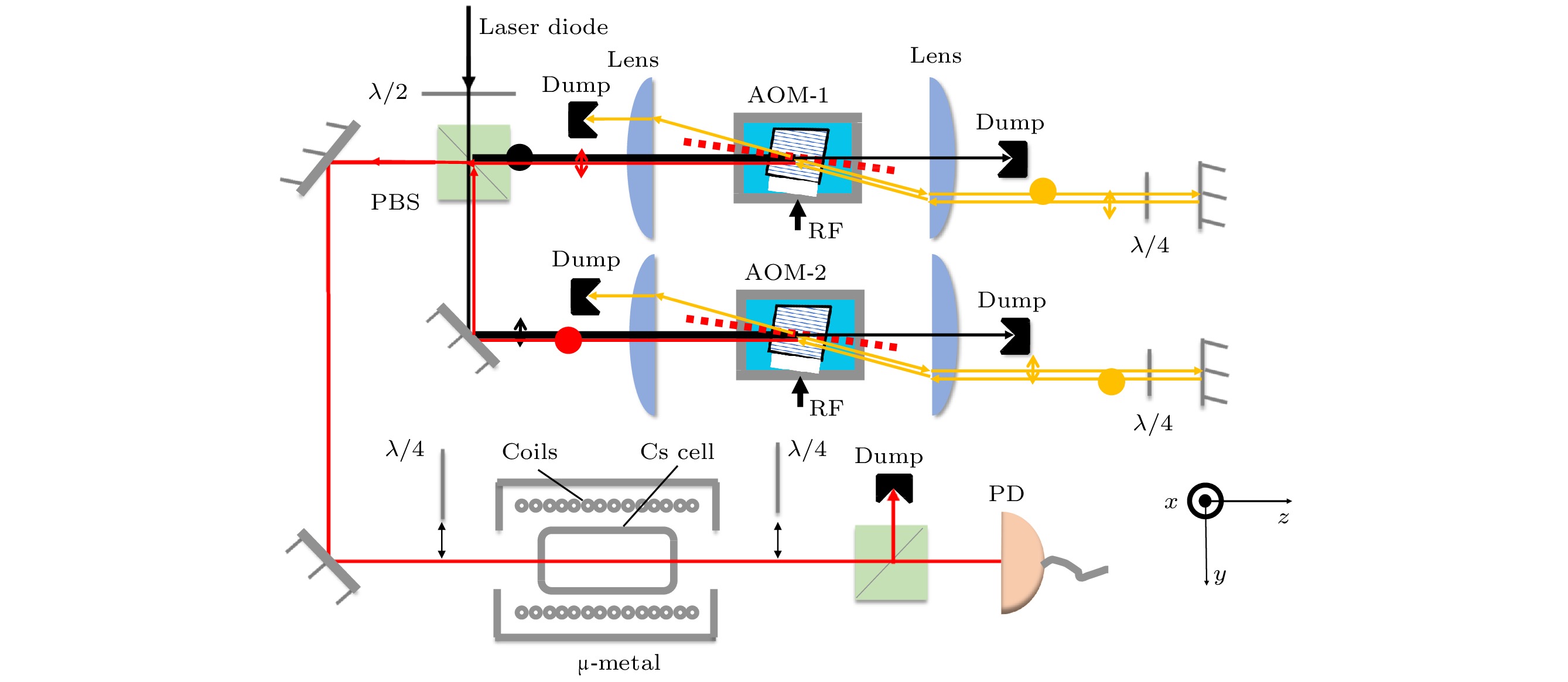
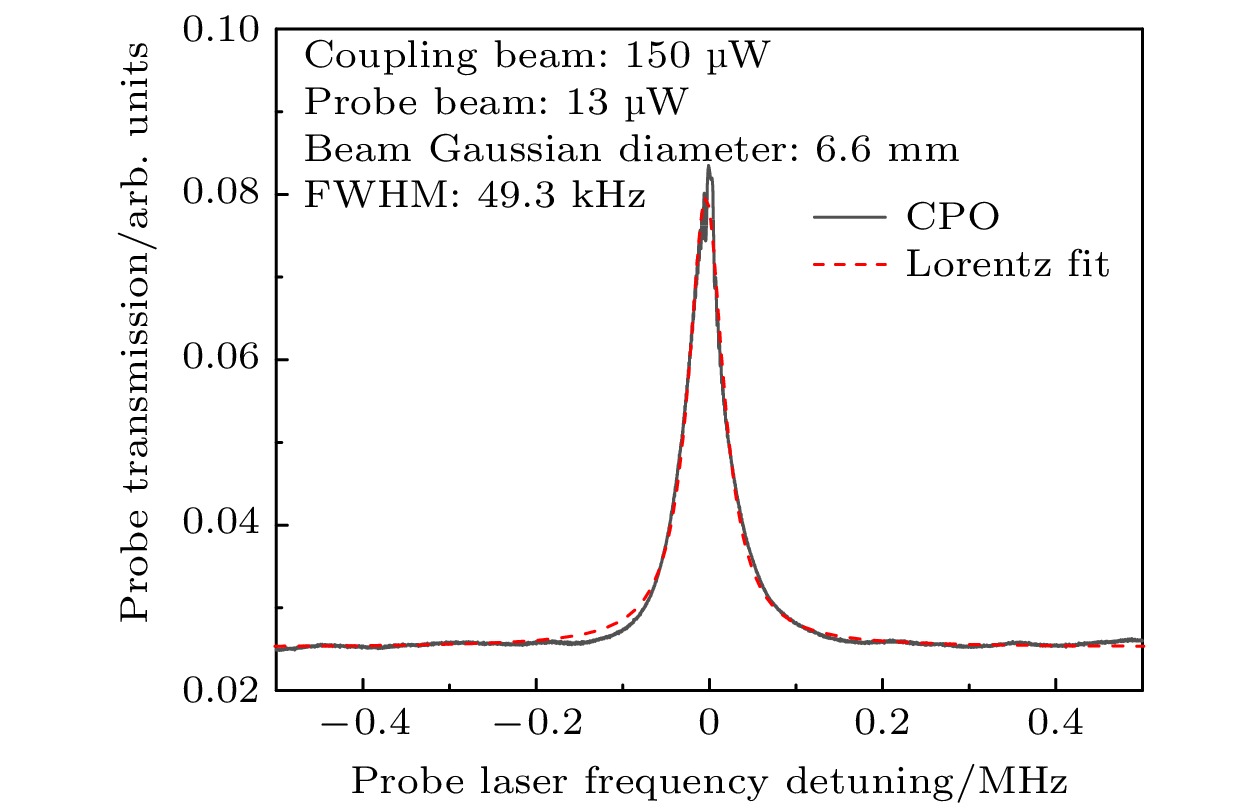
$6{{\rm{S}}_{1/2}}\left( {F = 3} \right) \to 6{{\rm{P}}_{3/2}}\left( {F' = 3} \right)$ transition. The frequencies of the two beams are shifted down by two independent double-passed acousto-optic modulators (AOM) to nearly resonate to Cesium$6{{\rm{S}}_{1/2}}\left( {F = 3} \right) \to 6{{\rm{P}}_{3/2}}\left( {F' = 2} \right)$ transition. The probe beam and the coupling beam are superposed at polarization beam splitter (PBS) cube and transmitted through the magnetically shielded cesium vapor cell in the same direction. The two beams have approximately the same Gaussian diameter of 6.6 mm. The beams are separated by another PBS behind the vapor cell, and the probe beam is detected by a photodiode. We realize the coherent population oscillation spectroscopy through the Cesium vapor cell at room temperature without buffer gas. The spectral linewidth is typically less than 50 kHz which is far below the spontaneous radiation linewidth(~5.2 MHz). The linewidth of coherent population oscillation spectroscopy of the Λ-type atomic energy level structure depends only on the population associated with the oscillation of multiple degenerate level systems except phase correlations of atomic states. Coherent population oscillation is beneficial to the obtaining of the narrow linewidth spectroscopy through the Rydberg atomic system with long excited state lifetime. Considering the importance of electric field measurement using Rydberg atoms, the method of coherent population oscillation can be used to improve the sensitivity of precise measurements based on Rydberg atoms.-
Keywords:
- coherent population oscillations /
- atomic population /
- cesium atomic vapor cell /
- Rydberg atom
[1] Zhang R, Xiao W, Ding Y D, Feng Y L, Peng X, Shen L, Sun C X, Wu T, Wu Y L, Yang Y C, Zheng Z Y, Zhang X Z, Chen J B, Guo H 2020 Sci. Adv. 6 eaba8792
Google Scholar
[2] Sheng J W, Wan S A, Sun Y F, Dou R S, Guo Y H, Wei K Q, He K Y, Qin J, Gao J H 2017 Rev. Sci. Instrum. 88 094304
Google Scholar
[3] Sedlacek J A, Schwettmann A, Kübler H, Shaffer J P 2013 Phys. Rev. Lett. 111 063001
[4] Schmittberger B L 2020 Opt. Express 28 38169
Google Scholar
[5] Webb K E, Xu Y Q, Erkintalo M, Murdoch S G 2013 Opt. Lett. 38 151
Google Scholar
[6] Wilson K, Little B, Gariepy G, Henderson R, Howell J, Faccio D 2017 Phys. Rev. A 95 023830
Google Scholar
[7] Raczyński A, Zaremba J, Zielińska-Kaniasty S 2004 Phys. Rev. A 69 043801
Google Scholar
[8] Nagel A, Graf L, Naumov A, Mariotti E, Biancalana V, Meschede D, Wynands R 1998 Europhys Lett. 44 31
Google Scholar
[9] Liu L, Guo T, Deng K, Liu X Y, Chen X Z 2007 Chin. Phys. Lett. 24 1883
Google Scholar
[10] Ryzhov I I, Kozlov G G, Smirnov D S, Glazov M M, Efimov Y P, Eliseev S A, Lovtcius V A, Petrov V V, Kavokin K V, Kavokin A V, Zapasskii V S 2016 Sci. Rep. 6 21062
Google Scholar
[11] Jing M Y, Hu Y, Ma J, Zhang H, Zhang L J, Xiao L T, Jia S T 2020 Nat. Phys. 16 911
Google Scholar
[12] Sedlacek J A, Schwettmann A, Kübler H, Löw R, Pfau T, Shaffer J P 2012 Nat. Phys. 8 819
Google Scholar
[13] Böhi P, Riedel M F, Hänsch T W, Treutlein P 2010 Appl. Phys. Lett. 97 051101
Google Scholar
[14] Hübner J, Berski F, Dahbashi R, Oestreich M 2014 Phys. Status Solidi B 251 1824
Google Scholar
[15] Klein M, Novikova I, Phillips D F, Walsworth R L 2006 J. Mod. Opt. 53 2583
Google Scholar
[16] Skvortsov M N, Ignatovich S M, Vishnyakov V I, Kvashnin N L, Mesenzova I S, Brazhnikov D V, Vasil'ev V A, Taichenachev A V, Yudin V I, Bagayev S N, Blinov I Y, Pal'chikov V G, Samokhvalov Y S, Parekhin D A 2020 Quantum Electron. 50 576
Google Scholar
[17] Baryshev V N, Osipenko G V, Aleinikov M S Blinov I Y 2019 Quantum Electron. 49 283
Google Scholar
[18] Thoumany P, Hänsch T, Stania G, Urbonas L, Becker T 2009 Opt. Lett. 34 1621
Google Scholar
[19] Li B, Li M, Jiang X J, Qian J, Li X L, Liu L, Wang Y Z 2019 Phys. Rev. A 99 042502
Google Scholar
[20] Maynard M A, Bretenaker F, Goldfarb F 2014 Phys. Rev. A 90 061801
Google Scholar
[21] Laupretre T, Kumar S, Berger P, Faoro R, Ghosh R, Bretenaker F, Goldfarb F 2012 Phys. Rev. A 85 051805
Google Scholar
[22] Almeida A J F, Barreiro S, Martins W S, Oliveira R A, Pruvost L, Felinto D, Tabosa J W R 2015 Opt. Lett. 40 2545
Google Scholar
[23] Almeida A J F, Sales J, Maynard M A, Lauprêtre T, Bretenaker F, Felinto D, Goldfarb F, Tabosa J W R 2014 Phys. Rev. A 90 043803
Google Scholar
-
图 1 铯原子系综相干布居振荡光谱 (a)铯原子超精细跃迁及Zeeman能级结构; (b)二能级结构; (c)三能级结构
Fig. 1. Schematic diagram of cesium atomic ensemble coherent population oscillations spectroscopy: (a) Hyperfine levels and Zeeman sublevels of the cesium D2 line; (b) two-level system and (c) three-level system associated with Zeeman sublevels of the ground and excited states.
图 2 (a)理论计算二能级模型与(b)三能级模型的透射线型
Fig. 2. Calculated transmission lines of (a) the two-level model and (b) the three-level model.
图 3 铯原子系综相干布居振荡光谱测量的实验装置示意图. PBS, 偏振分束棱镜; AOM, 声光调制器; PD, 光电二极管
Fig. 3. Schematic diagram of experimental setup for measuring cesium atomic ensemble coherent population oscillations spectrum. PBS, polarizing beam splitter; AOM, acousto-optic modulator; PD, photodiode.
图 4 典型的铯原子相干布居振荡光谱, 虚线为Lorentz拟合
Fig. 4. Coherent population oscillations spectrum of cesium atoms.
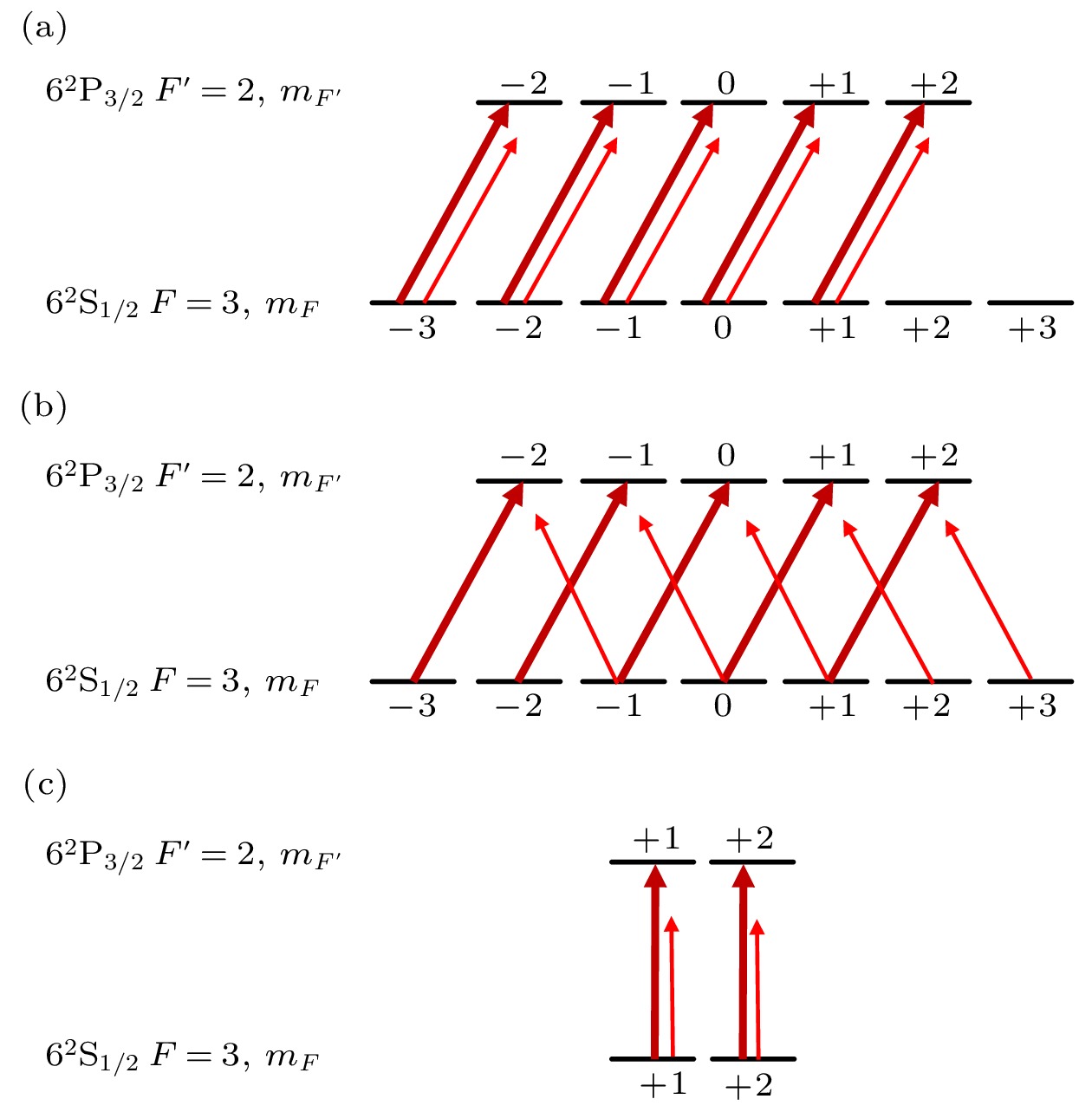
图 5 不同磁场方向, 光场k方向, 不同原子能级构型的光偏振组合 (a)
$ \sigma ^+-\sigma ^+$ 构型; (b)$ \sigma ^+-\sigma ^-$ 构型; (c)$ \pi -\pi $ 构型Fig. 5. Energy-level scheme for the interaction of the cesium D2 line with different laser polarization and magnetic fields: (a)
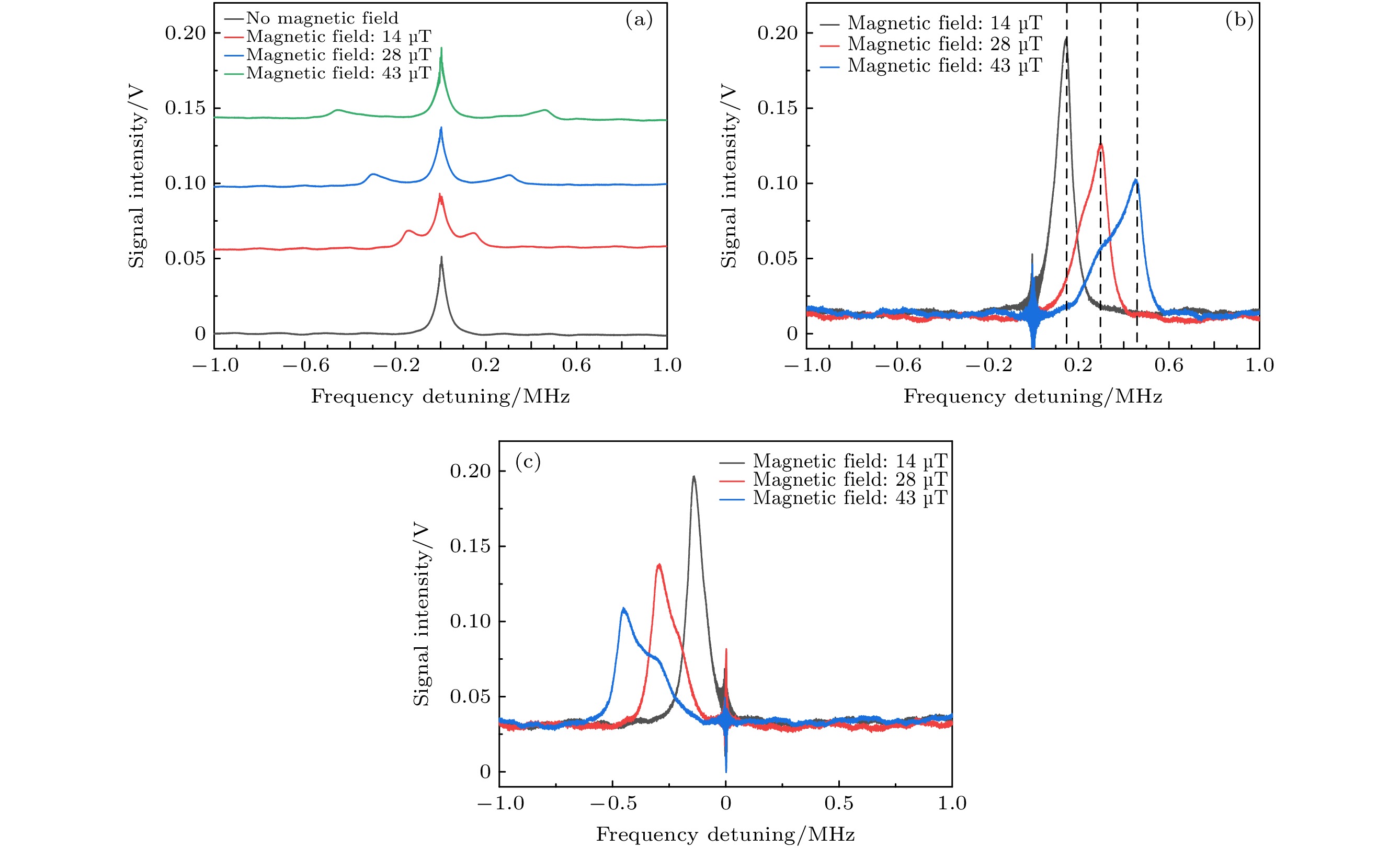
$ \sigma ^+-\sigma ^+$ ; (b)$ \sigma ^+-\sigma ^-$ ; (c)$ \pi -\pi $ .
图 6 探测光不同偏振状态时磁场环境中的CPO和EIT光谱 (a)线偏振光, (151 ± 9) kHz (红线), (312 ± 11) kHz (蓝线), (460 ± 25) kHz (绿线); (b)
$ {\sigma ^ + }$ 圆偏振光, (153 ± 9) kHz (黑线), (314 ± 11) kHz (红线), (475 ± 25) kHz (蓝线); (c)$ {\sigma ^ - }$ 圆偏振光, (–155 ± 7) kHz (黑线), (–309 ± 15) kHz (红线), (–474 ± 22) kHz (蓝线)Fig. 6. Coherent population oscillations spectrum in magnetic field with different polarzaiton of probe beam: (a) linear polarization, (151 ± 9) kHz (red), (312 ± 11) kHz (blue), (460 ± 25) kHz (green); (b)
$ {\sigma ^ + }$ circular polarization, (153 ± 9) kHz (black), (314 ± 11) kHz (red), (475 ± 25) kHz (blue); (c)$ {\sigma ^ - }$ circular polarization, (–155 ± 7) kHz (black), (–309 ± 15) kHz (red), (–474 ± 22) kHz (blue).
图 7 不同功率下铯原子相干布居振荡光谱的幅度与线宽
Fig. 7. Amplitude and linewidth of coherent population oscillations spectroscopy of cesium atoms with different power.
-
[1] Zhang R, Xiao W, Ding Y D, Feng Y L, Peng X, Shen L, Sun C X, Wu T, Wu Y L, Yang Y C, Zheng Z Y, Zhang X Z, Chen J B, Guo H 2020 Sci. Adv. 6 eaba8792
Google Scholar
[2] Sheng J W, Wan S A, Sun Y F, Dou R S, Guo Y H, Wei K Q, He K Y, Qin J, Gao J H 2017 Rev. Sci. Instrum. 88 094304
Google Scholar
[3] Sedlacek J A, Schwettmann A, Kübler H, Shaffer J P 2013 Phys. Rev. Lett. 111 063001
[4] Schmittberger B L 2020 Opt. Express 28 38169
Google Scholar
[5] Webb K E, Xu Y Q, Erkintalo M, Murdoch S G 2013 Opt. Lett. 38 151
Google Scholar
[6] Wilson K, Little B, Gariepy G, Henderson R, Howell J, Faccio D 2017 Phys. Rev. A 95 023830
Google Scholar
[7] Raczyński A, Zaremba J, Zielińska-Kaniasty S 2004 Phys. Rev. A 69 043801
Google Scholar
[8] Nagel A, Graf L, Naumov A, Mariotti E, Biancalana V, Meschede D, Wynands R 1998 Europhys Lett. 44 31
Google Scholar
[9] Liu L, Guo T, Deng K, Liu X Y, Chen X Z 2007 Chin. Phys. Lett. 24 1883
Google Scholar
[10] Ryzhov I I, Kozlov G G, Smirnov D S, Glazov M M, Efimov Y P, Eliseev S A, Lovtcius V A, Petrov V V, Kavokin K V, Kavokin A V, Zapasskii V S 2016 Sci. Rep. 6 21062
Google Scholar
[11] Jing M Y, Hu Y, Ma J, Zhang H, Zhang L J, Xiao L T, Jia S T 2020 Nat. Phys. 16 911
Google Scholar
[12] Sedlacek J A, Schwettmann A, Kübler H, Löw R, Pfau T, Shaffer J P 2012 Nat. Phys. 8 819
Google Scholar
[13] Böhi P, Riedel M F, Hänsch T W, Treutlein P 2010 Appl. Phys. Lett. 97 051101
Google Scholar
[14] Hübner J, Berski F, Dahbashi R, Oestreich M 2014 Phys. Status Solidi B 251 1824
Google Scholar
[15] Klein M, Novikova I, Phillips D F, Walsworth R L 2006 J. Mod. Opt. 53 2583
Google Scholar
[16] Skvortsov M N, Ignatovich S M, Vishnyakov V I, Kvashnin N L, Mesenzova I S, Brazhnikov D V, Vasil'ev V A, Taichenachev A V, Yudin V I, Bagayev S N, Blinov I Y, Pal'chikov V G, Samokhvalov Y S, Parekhin D A 2020 Quantum Electron. 50 576
Google Scholar
[17] Baryshev V N, Osipenko G V, Aleinikov M S Blinov I Y 2019 Quantum Electron. 49 283
Google Scholar
[18] Thoumany P, Hänsch T, Stania G, Urbonas L, Becker T 2009 Opt. Lett. 34 1621
Google Scholar
[19] Li B, Li M, Jiang X J, Qian J, Li X L, Liu L, Wang Y Z 2019 Phys. Rev. A 99 042502
Google Scholar
[20] Maynard M A, Bretenaker F, Goldfarb F 2014 Phys. Rev. A 90 061801
Google Scholar
[21] Laupretre T, Kumar S, Berger P, Faoro R, Ghosh R, Bretenaker F, Goldfarb F 2012 Phys. Rev. A 85 051805
Google Scholar
[22] Almeida A J F, Barreiro S, Martins W S, Oliveira R A, Pruvost L, Felinto D, Tabosa J W R 2015 Opt. Lett. 40 2545
Google Scholar
[23] Almeida A J F, Sales J, Maynard M A, Lauprêtre T, Bretenaker F, Felinto D, Goldfarb F, Tabosa J W R 2014 Phys. Rev. A 90 043803
Google Scholar
下载:
计量
- 文章访问数: 5422
- PDF下载量: 124
- 被引次数: 0
