基于一维耦合腔光子晶体的声光可调谐平顶滤波器的研究

张若羽; 李培丽

doi:10.7498/aps.70.20201461

摘要

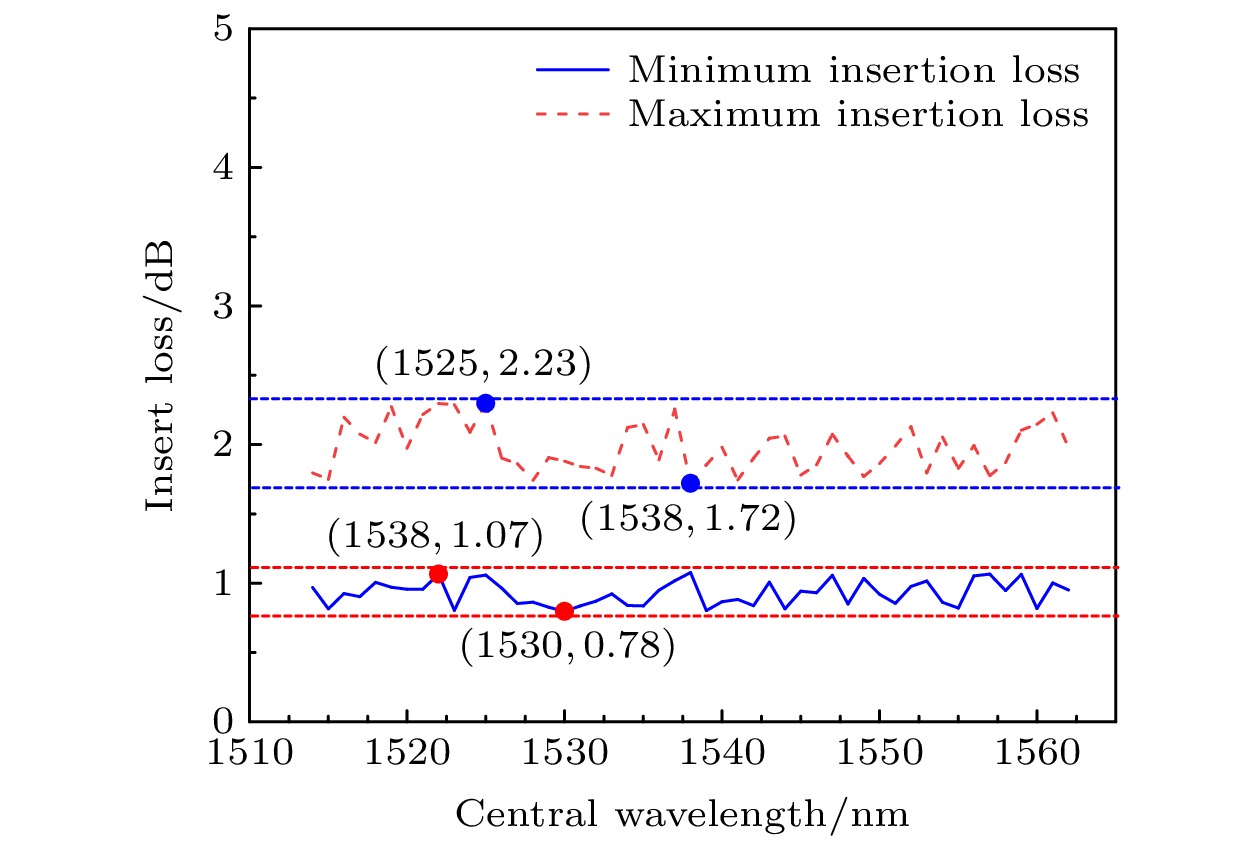
本文利用一维耦合腔光子晶体, 提出了一种声光可调谐平顶滤波器. 该滤波器利用声光效应, 通过改变超声波频率使一维耦合腔光子晶体透射谱的平顶滤波器的中心波长产生漂移, 从而实现可调谐的滤波功能. 基于传输矩阵法和声光效应理论, 建立了这种平顶滤波器的理论模型; 利用COMSOL软件, 对平顶滤波器的矩形度、通带带宽、插入损耗、可调谐特性、加工精度进行仿真研究. 研究结果表明, 通过施加频率为6—11 MHz的超声波, 可实现通带带宽为5—6 nm及中心波长在1514—1562 nm范围内可调谐的平顶滤波器; 在可调谐范围内通带带宽内插入损耗不超过2.23 dB, 最低仅为0.78 dB, 矩形度最低可达1.4; 加工误差在$ \pm 10\;{\rm{nm}}$内平顶滤波器的中心波长、矩形度、插入损耗、通带带宽出现的偏差很小. 该平顶滤波器具有易于设计和集成、通带平坦、可调谐范围宽、通带带宽稳定、插入损耗低、品质因素高的特点, 在光开关、可调谐光纤激光器、光纤传感等光通信领域有重要应用.

关键词:

Abstract

In this paper, an acousto-optic tunable flat top filter is proposed by using one-dimensional coupled-cavity photonic crystal, and two kinds of materials, i.e. magnesium fluoride and tellurium dioxide, are selected. Based on the theory of acousto-optic effect, the thickness and refractive index of one-dimensional coupled cavity photonic crystal acousto-optic medium are changed by varying the ultrasonic frequency. After the parameters of acousto-optic medium are changed, the central wavelength of flat top filter of transmission spectrum shifts toward the short wave direction, thus realizing tunable filtering function. Based on the transfer matrix method and the theory of acousto-optic effect, the theoretical model of the flat top filter is established. The rectangularity, passband bandwidth, insertion loss and tunability of flat top filter are simulated by COMSOL software. The results show that the tuning effect can be achieved by applying a certain frequency of ultrasound in the case of different ultrasonic amplitudes. The decreasing trends of transmittance are basically identical in the process of changing ultrasonic frequency in the case of different amplitudes. When the central wavelength of the flat top filter increases from 1510 nm to 1514 nm, the transmissivity corresponding to the central wavelength increases sharply from 37% to 90%; when the central wavelength of the flat top filter continuously increases to 1562 nm, the transmittance corresponding to the central wavelength increasing gently from 90% to 97% in the case of different amplitudes. Considering the transmissivity required to exceed 90% in the passband of flat top filter and the cost of ultrasonic generator, the ultrasonic wave with an amplitude of 0.4 nm is selected as the research object. The flat top filter with 5–6 nm central wavelength and 1514–1562 nm tunable flat top filter can be realized by applying ultrasonic wave with the frequency in a range of 6–11 MHz. In the tunable range, the highest insertion loss is only 2.23 dB, the lowest is only 0.78 dB, and the lowest rectangularity is 1.4. In a practical flat top filter with machining error within 5 cm, the deviation of center wavelength, rectangularity, insertion loss and passband bandwidth of flat top filter are all very small. The flat top filter has the characteristics of easy design and integration, flat passband, wide tunable range, stable passband bandwidth, low insertion loss and high quality factor. It has important applications in optical communication fields such as optical switch, tunable fiber laser and fiber sensing.

Keywords:

flat top filter /
acousto-optic effect /
one-dimensional coupled-cavity photonic crystals /
tunable

作者及机构信息

南京邮电大学电子与光学工程学院, 南京　210023

通信作者: 李培丽, lipl@njupt.edu.cn

Authors and contacts

Department of Opto-Electronic Engineering, Nanjing University of Posts and Telecommunications, Nanjing 210023, China

Corresponding author: Li Pei-Li, lipl@njupt.edu.cn

文章全文 : translate this paragraph

参考文献

[1]	林洪榕, 迟晓玲, 李利军 2001 激光与光电子学进展 11 31 Lin H R, Chi X L, Li L J 2001 Las. Optoelect. Prog. 11 31
[2]	Liu J, Tao L 2019 Opt. Commun. 459 125038 Google Scholar
[3]	顾培夫, 陈海星, 秦小芸, 刘旭 2005 54 773 Google Scholar Gu P F, Chen H X, Qin X Y, Liu X 2005 Acta Phys. Sin. 54 773 Google Scholar
[4]	常凌颖, 郑爱国, 宋晶晶 2018 应用光学 39 359 Google Scholar Chang L Y, Zheng A G, Song J J 2018 JAO 39 359 Google Scholar
[5]	Magdich L, Chamorovskii A, Shidlovskii V, Yakubovich S 2020 IEEE J. Quantum Electron 50 136 Google Scholar
[6]	左涛, 赵新杰, 岳宏卫, 方兰, 阎少林, 王小坤 2009 58 4194 Google Scholar Zuo T, Zhao X J, Yue H W, Fang L, Yan S L, Wang X K 2009 Acta Phys. Sin. 58 4194 Google Scholar
[7]	张娟, 于帅, 郭森, 李雪 2011 中国激光 1 0105005 Google Scholar Juan Z, Shuai Y, Sen G, Xue L 2011 Chin J Las 1 0105005 Google Scholar
[8]	赵辉 2009 硕士学位论文 (北京: 北京化工大学) Zhao H 2009 M. S. Thesis (Beijing: Beijing University of Chemical Technology) (in Chinese)
[9]	Suh W, Fan S 2003 Opt. Lett. 28 1763 Google Scholar
[10]	Rossi K, Baletto F 2017 Phys. Chem. Chem. Phys. 19 11057 Google Scholar
[11]	Okayama H, Onawa Y, Shimura D, Takahashi H, Yaegashi H, Sasaki H 2019 Electron. Lett. 55 107 Google Scholar
[12]	戚志明, 梁文耀 2016 65 074201 Google Scholar Qi Z M, Liang W Y 2016 Acta Phys. Sin. 65 074201 Google Scholar
[13]	Xiao L, Liu Y, Wang W, Geng F 2006 Chin. Phys. Lett. 23 645 Google Scholar
[14]	李培丽, 高辉, 栾开智, 陆云清 2020 光谱学与光谱分析 40 650 Google Scholar Li P L, Gao H, Luan K Z, Lu Y Q 2020 Spectrosc. Spect. Anal. 40 650 Google Scholar
[15]	李乾利, 温廷敦, 许丽萍 2013 62 184212 Google Scholar Li Q L, Wen T D, Xu L P 2013 Acta Phys. Sin. 62 184212 Google Scholar
[16]	Bandyopadhyay R, Chakraborty R 2015 Opt. Eng. 54 117105 Google Scholar
[17]	刘菲, 金杰, 李可佳 2011 光学学报 10 1023003 Google Scholar Liu F, Jin J, Li K J 2011 Acta Optic. Sin. 10 1023003 Google Scholar
[18]	Bai J, Li X, Zhou Q, Ni K, Wang X 2019 Opt. Express 27 10961 Google Scholar
[19]	Chung M, Wang S 2006 Jpn. J. Appl. Phys. 45 841 Google Scholar
[20]	Yang L, Zhou Y, Zhang C, Xiao Q 2017 Sci. Rep. 7 14237 Google Scholar
[21]	Inoue G, Wang P, Li H 2016 Opt. Express 24 5442 Google Scholar
[22]	周婷婷, 谢卉, 孙莉萍, 胡强高 2011 光通信研究 37 23 Google Scholar Zhou T T, Xie H, Sun L P, Hu Q G 2011 Stud. Opt. Commun. 37 23 Google Scholar
[23]	Jiang F, Yu Y, Cao T, Tang H, Dong J, Zhang X 2016 Opt. Express 41 3301 Google Scholar

施引文献

图 1 基于一维耦合腔光子晶体中声光效应的可调谐平顶滤波器结构图及超声波波形图

Fig. 1. Structure diagram and ultrasonic waveform of tunable flat top filter based on acousto-optic effect in one-dimensional coupled-cavity photonic crystals.

下载: 全尺寸图片幻灯片

图 2 一维耦合腔光子晶体的透射谱

Fig. 2. Transmission spectrum of one-dimensional coupled-cavity photonic crystal.

下载: 全尺寸图片幻灯片

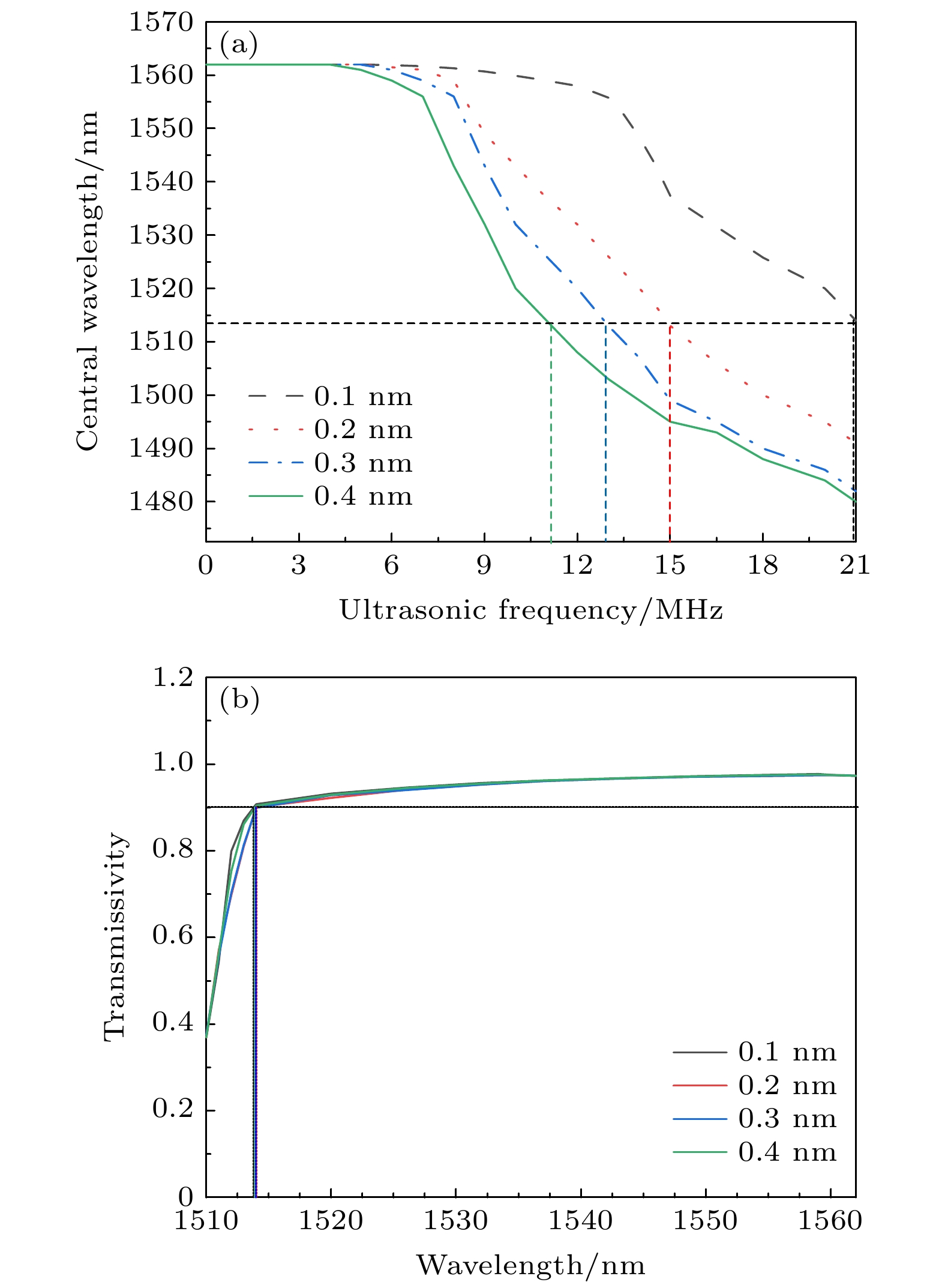
图 3 不同超声波振幅下一维耦合腔光子晶体透射谱中心波长随超声波频率的改变　(a)平顶滤波器中心波长与超声波频率的关系图; (b)平顶滤波器中心波长与透射率的关系图

Fig. 3. Variation of the central wavelength of transmission spectrum of one-dimensional coupled-cavity photonic crystals with different ultrasonic amplitudes: (a) Relationship between the center wavelength of flat top filter and ultrasonic frequency; (b) relationship between the center wavelength of flat top filter and transmissivity.

下载: 全尺寸图片幻灯片

图 4 平顶滤波器施加频率8, 11 MHz的超声波和不加超声波的透射谱

Fig. 4. Transmission spectra of flat top filter with ultrasonic wave at 8, 11 MHz and without ultrasonic wave.

下载: 全尺寸图片幻灯片

图 5 平顶滤波器中心波长与矩形度的关系图

Fig. 5. Relationship between center wavelength of flat top filter and rectangularity.

下载: 全尺寸图片幻灯片

图 6 平顶滤波器中心波长与通带带宽的关系

Fig. 6. Relationship between center wavelength of flat top filter and passband bandwidth.

下载: 全尺寸图片幻灯片

图 7 平顶滤波器中心波长与插入损耗的关系图

Fig. 7. Relationship between center wavelength of flat top filter and insert loss.

下载: 全尺寸图片幻灯片

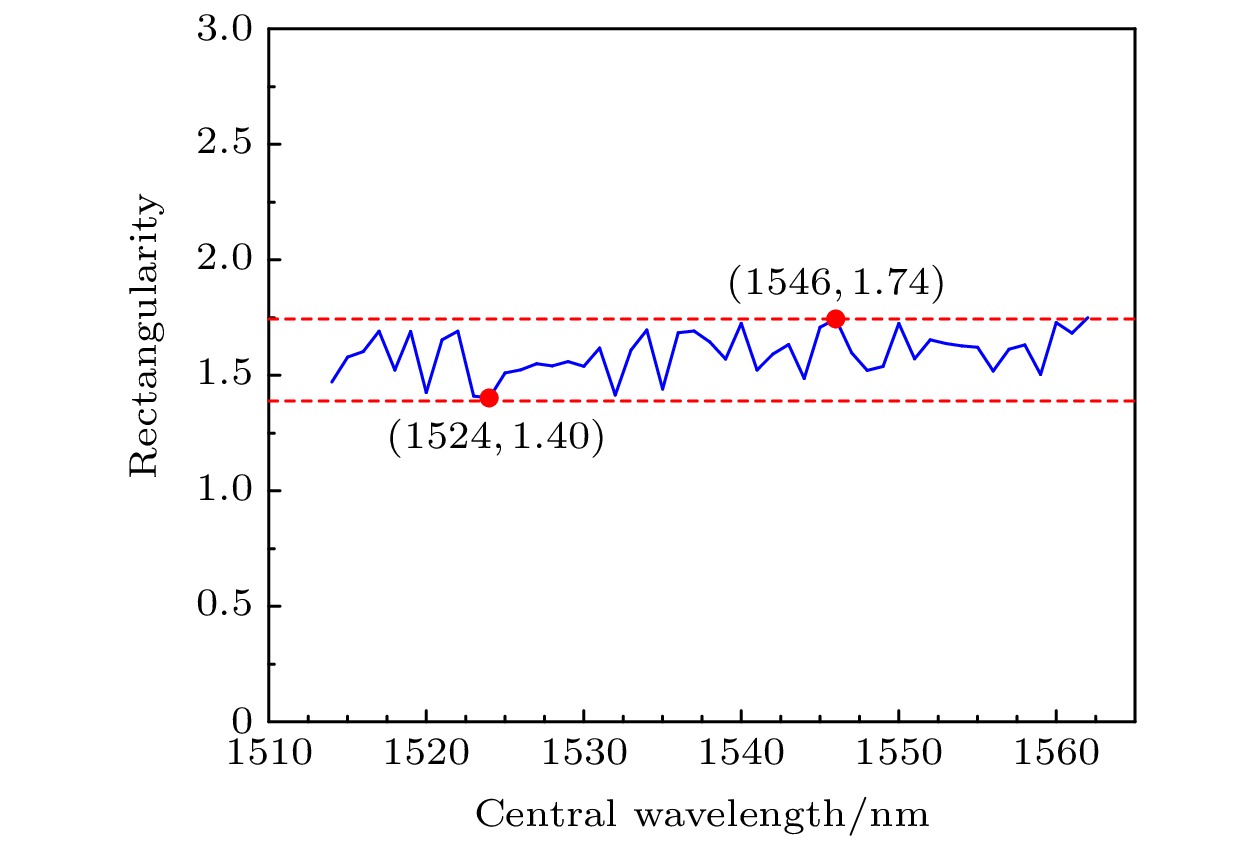
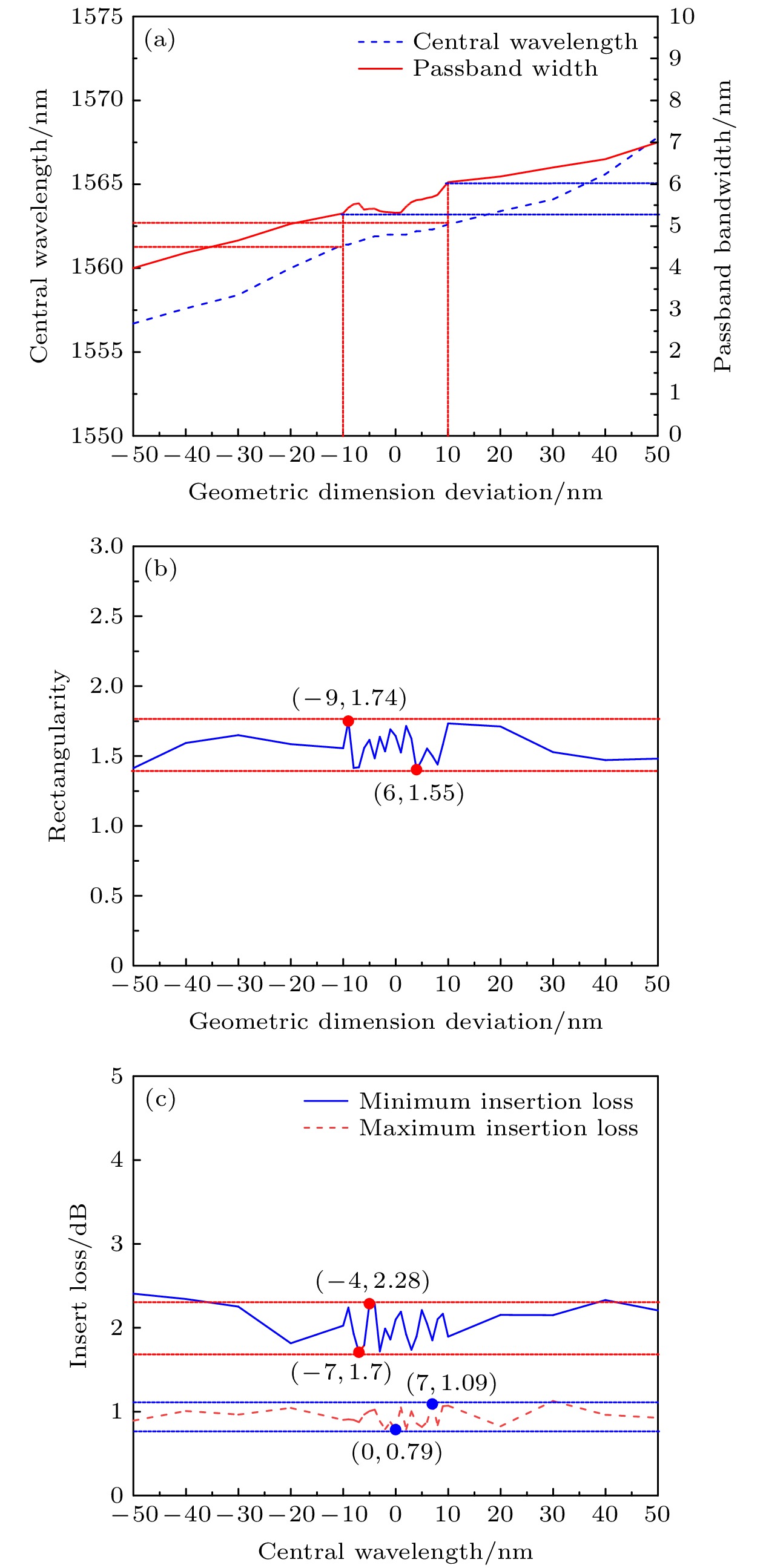
图 8 一维光子晶体几何尺寸偏差与相关参数的关系　(a) 一维光子晶体几何尺寸偏差与平顶滤波器中心波长和通带带宽的关系图; (b) 一维光子晶体几何尺寸偏差与平顶滤波器矩形度的关系图; (c) 一维光子晶体几何尺寸偏差与平顶滤波器插入损耗的关系图

Fig. 8. Relationship between geometric size deviation and related parameters of one-dimensional photonic crystal: (a) Relationship between geometric dimension deviation of one dimensional photonic crystal and central wavelength or passband bandwidth of flat top filter; (b) relationship between the geometric size deviation of one-dimensional photonic crystal and rectangularity of flat top filter; (c) relationship between the geometric size deviation of one-dimensional photonic crystal and the insert loss of flat top filter

下载: 全尺寸图片幻灯片

表 1 不同平顶滤波器性能参数比较

Table 1. Comparison of performance parameters of different flat top filters.

参数来源	采用技术	中心波长	通带带宽	是否可调谐	调谐范围
本文	一维耦合腔光子晶体	1562 nm	5.2 nm	是	1514—1562 nm
文献[2]	棱镜耦合平面光波导	633 nm	0.3 nm	是	622—652 nm
文献[20]	金属-绝缘体-金属环形谐振器	3.5 GHz	1.5 GHz	否
文献[21]	级联长周期光纤光栅	1574.5 nm	13 nm	否
文献[22]	MEMS技术	1545 nm	0.2 nm	是	1525—1565 nm
文献[23]	F-P半导体光放大器	10 GHz	1 GHz	是	7—9 GHz
文献[7]	一维光子晶体	193.4 GHz	0.02 THz	否

下载: 导出CSV

map

[1]	林洪榕, 迟晓玲, 李利军 2001 激光与光电子学进展 11 31 Lin H R, Chi X L, Li L J 2001 Las. Optoelect. Prog. 11 31
[2]	Liu J, Tao L 2019 Opt. Commun. 459 125038 Google Scholar
[3]	顾培夫, 陈海星, 秦小芸, 刘旭 2005 54 773 Google Scholar Gu P F, Chen H X, Qin X Y, Liu X 2005 Acta Phys. Sin. 54 773 Google Scholar
[4]	常凌颖, 郑爱国, 宋晶晶 2018 应用光学 39 359 Google Scholar Chang L Y, Zheng A G, Song J J 2018 JAO 39 359 Google Scholar
[5]	Magdich L, Chamorovskii A, Shidlovskii V, Yakubovich S 2020 IEEE J. Quantum Electron 50 136 Google Scholar
[6]	左涛, 赵新杰, 岳宏卫, 方兰, 阎少林, 王小坤 2009 58 4194 Google Scholar Zuo T, Zhao X J, Yue H W, Fang L, Yan S L, Wang X K 2009 Acta Phys. Sin. 58 4194 Google Scholar
[7]	张娟, 于帅, 郭森, 李雪 2011 中国激光 1 0105005 Google Scholar Juan Z, Shuai Y, Sen G, Xue L 2011 Chin J Las 1 0105005 Google Scholar
[8]	赵辉 2009 硕士学位论文 (北京: 北京化工大学) Zhao H 2009 M. S. Thesis (Beijing: Beijing University of Chemical Technology) (in Chinese)
[9]	Suh W, Fan S 2003 Opt. Lett. 28 1763 Google Scholar
[10]	Rossi K, Baletto F 2017 Phys. Chem. Chem. Phys. 19 11057 Google Scholar
[11]	Okayama H, Onawa Y, Shimura D, Takahashi H, Yaegashi H, Sasaki H 2019 Electron. Lett. 55 107 Google Scholar
[12]	戚志明, 梁文耀 2016 65 074201 Google Scholar Qi Z M, Liang W Y 2016 Acta Phys. Sin. 65 074201 Google Scholar
[13]	Xiao L, Liu Y, Wang W, Geng F 2006 Chin. Phys. Lett. 23 645 Google Scholar
[14]	李培丽, 高辉, 栾开智, 陆云清 2020 光谱学与光谱分析 40 650 Google Scholar Li P L, Gao H, Luan K Z, Lu Y Q 2020 Spectrosc. Spect. Anal. 40 650 Google Scholar
[15]	李乾利, 温廷敦, 许丽萍 2013 62 184212 Google Scholar Li Q L, Wen T D, Xu L P 2013 Acta Phys. Sin. 62 184212 Google Scholar
[16]	Bandyopadhyay R, Chakraborty R 2015 Opt. Eng. 54 117105 Google Scholar
[17]	刘菲, 金杰, 李可佳 2011 光学学报 10 1023003 Google Scholar Liu F, Jin J, Li K J 2011 Acta Optic. Sin. 10 1023003 Google Scholar
[18]	Bai J, Li X, Zhou Q, Ni K, Wang X 2019 Opt. Express 27 10961 Google Scholar
[19]	Chung M, Wang S 2006 Jpn. J. Appl. Phys. 45 841 Google Scholar
[20]	Yang L, Zhou Y, Zhang C, Xiao Q 2017 Sci. Rep. 7 14237 Google Scholar
[21]	Inoue G, Wang P, Li H 2016 Opt. Express 24 5442 Google Scholar
[22]	周婷婷, 谢卉, 孙莉萍, 胡强高 2011 光通信研究 37 23 Google Scholar Zhou T T, Xie H, Sun L P, Hu Q G 2011 Stud. Opt. Commun. 37 23 Google Scholar
[23]	Jiang F, Yu Y, Cao T, Tang H, Dong J, Zhang X 2016 Opt. Express 41 3301 Google Scholar

[1]	吕宇曦, 王晨, 段添期, 赵彤, 常朋发, 王安帮. 级联声光器件与回音壁模式微腔实现非对称传输. , 2024, 73(1): 014101. doi: 10.7498/aps.73.20230653
[2]	王涛, 彭雪芳, 贺亮, 沈小雨, 朱仁江, 蒋丽丹, 佟存柱, 宋晏蓉, 张鹏. 509 nm高功率宽调谐外腔面发射激光器. , 2024, 73(12): 124204. doi: 10.7498/aps.73.20240499
[3]	成佳, 伍亚东, 晏日, 彭雪芳, 朱仁江, 王涛, 蒋丽丹, 佟存柱, 宋晏蓉, 张鹏. 基于外腔面发射激光器腔内三倍频的可调谐紫外激光器. , 2024, 73(8): 084202. doi: 10.7498/aps.73.20231923
[4]	王明军, 王婉柔, 李勇俊. 利用平面声场对非均匀大气介质光波传输相位的调控. , 2022, 71(16): 164302. doi: 10.7498/aps.71.20220484
[5]	刘紫玉, 亓丽梅, 道日娜, 戴林林, 武利勤. 基于VO₂的波束可调太赫兹天线. , 2022, 71(18): 188703. doi: 10.7498/aps.71.20220817
[6]	王武越, 于宇, 李云飞, 王汞, 李凯, 王志永, 宋长禹, 李森森, 李宇海, 刘彤宇, 闫秀生, 王雨雷, 吕志伟. 脊型悬浮波导布里渊激光器. , 2022, 71(2): 024203. doi: 10.7498/aps.71.20211539
[7]	王武越, Yu Yu, 李云飞, 王汞, 李凯, 王志勇, 宋长禹, 李森森, 李宇海, 刘彤宇, 闫秀生, 王雨雷, 吕志伟. 脊型悬浮波导布里渊激光器（光电技术与应用）. , 2021, (): . doi: 10.7498/aps.70.20211539
[8]	王志鹏, 关宝璐, 张峰, 杨嘉炜. 内腔亚波长光栅液晶可调谐垂直腔面发射激光器. , 2021, 70(22): 224208. doi: 10.7498/aps.70.20210957
[9]	张若羽, 李培丽, 高辉. 基于光学tamm态的声光开关的研究. , 2020, 69(16): 164204. doi: 10.7498/aps.69.20200396
[10]	熊梦杰, 李进延, 罗兴, 沈翔, 彭景刚, 李海清. 新型高双折射微结构纤芯光子晶体光纤的可调谐超连续谱的特性研究. , 2017, 66(9): 094204. doi: 10.7498/aps.66.094204
[11]	刘超, 裴丽, 吴良英, 王一群, 翁思俊, 余少伟. 基于光纤叠栅的全光纤声光可调谐滤波器的特性分析. , 2015, 64(17): 174207. doi: 10.7498/aps.64.174207
[12]	贾石, 于晋龙, 王菊, 王文睿, 王子雄, 陈斌. 基于波长双环路结构的新型光电振荡器的研究. , 2015, 64(15): 154204. doi: 10.7498/aps.64.154204
[13]	孟祥昊, 刘华刚, 黄见洪, 戴殊韬, 邓晶, 阮开明, 陈金明, 林文雄. Ba1-xB2-y-zO4SixAlyGaz晶体和频可调谐深紫外飞秒激光器. , 2015, 64(16): 164205. doi: 10.7498/aps.64.164205
[14]	阴明, 周寿桓, 冯国英. 可调谐准相位匹配高效宽带二次谐波转换. , 2012, 61(23): 234206. doi: 10.7498/aps.61.234206
[15]	于国君, 卜胜利, 王响, 纪红柱. 基于硅柱-磁性液体体系的光子晶体的可调谐负折射特性研究. , 2012, 61(19): 194703. doi: 10.7498/aps.61.194703
[16]	郭展, 范飞, 白晋军, 牛超, 常胜江. 基于磁光子晶体的磁控可调谐太赫兹滤波器和开关. , 2011, 60(7): 074218. doi: 10.7498/aps.60.074218
[17]	周可余, 叶辉, 甄红宇, 尹伊, 沈伟东. 基于压电聚合物薄膜可调谐Fabry-Perot滤波器的研究. , 2010, 59(1): 365-369. doi: 10.7498/aps.59.365
[18]	杨薇, 刘迎, 肖立峰, 高树理. 两级串联声光可调谐滤波器旁瓣抑制的研究. , 2009, 58(1): 328-332. doi: 10.7498/aps.58.328
[19]	云茂金, 万勇, 孔伟金, 王美, 刘均海, 梁伟. 可调谐位相型光瞳滤波器的横向光学超分辨和轴向扩展焦深. , 2008, 57(1): 194-199. doi: 10.7498/aps.57.194
[20]	董新永, 赵春柳, 关柏鸥, 谭华耀, 袁树忠, 开桂云, 董孝义. 可调谐光纤环形腔激光器输出特性的理论与实验研究. , 2002, 51(12): 2750-2755. doi: 10.7498/aps.51.2750

计量

文章访问数: 5782
PDF下载量: 89
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板