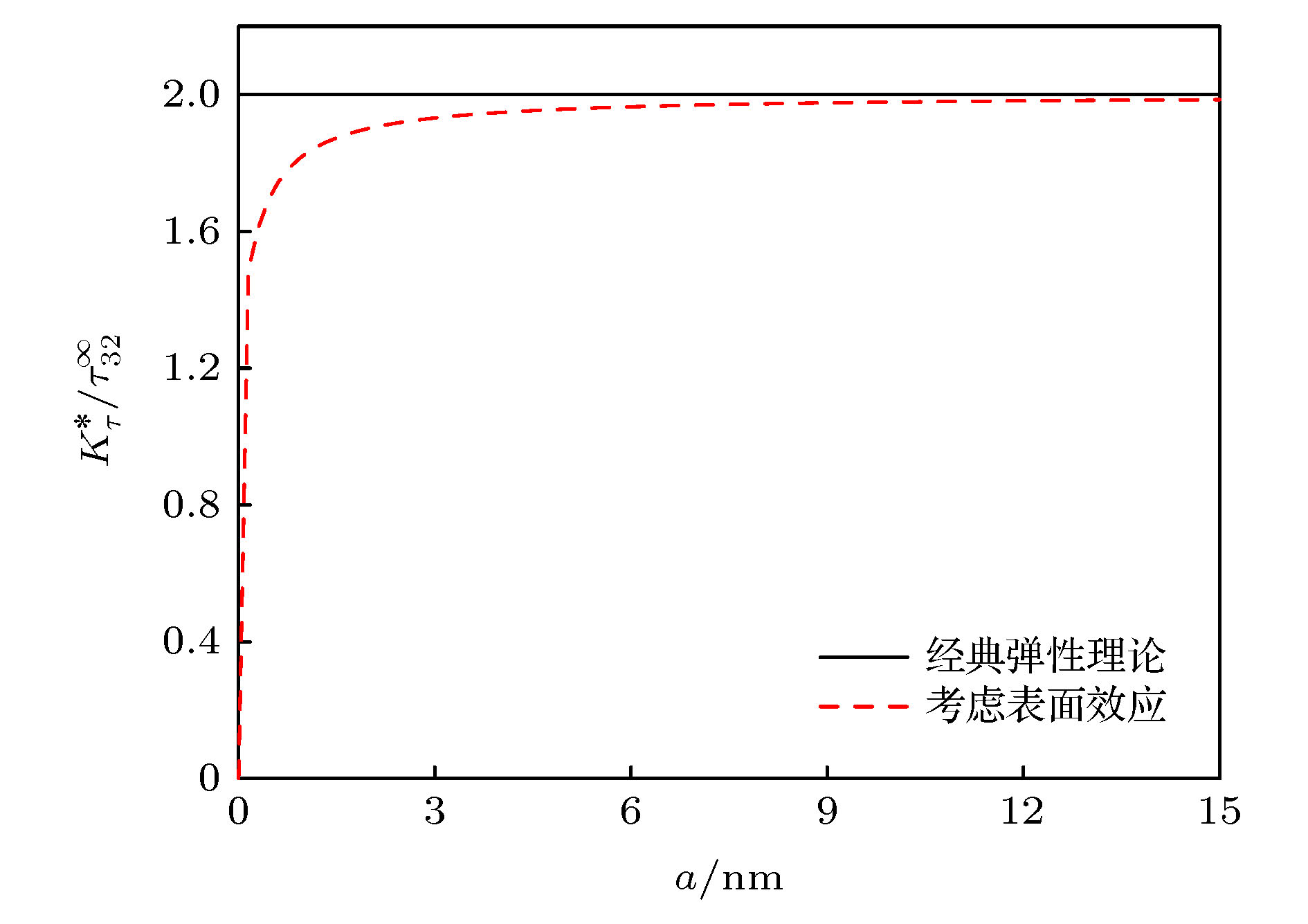
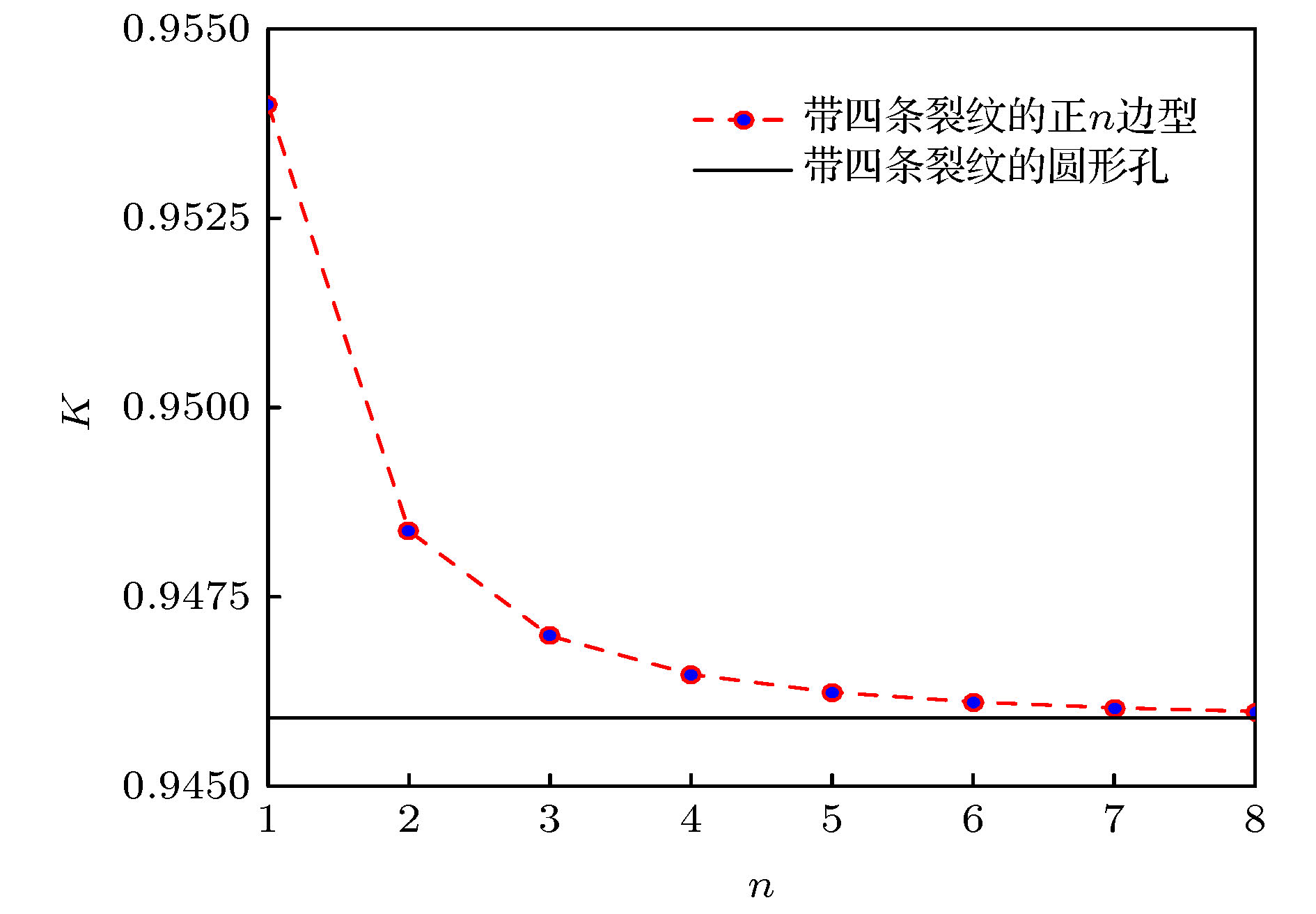
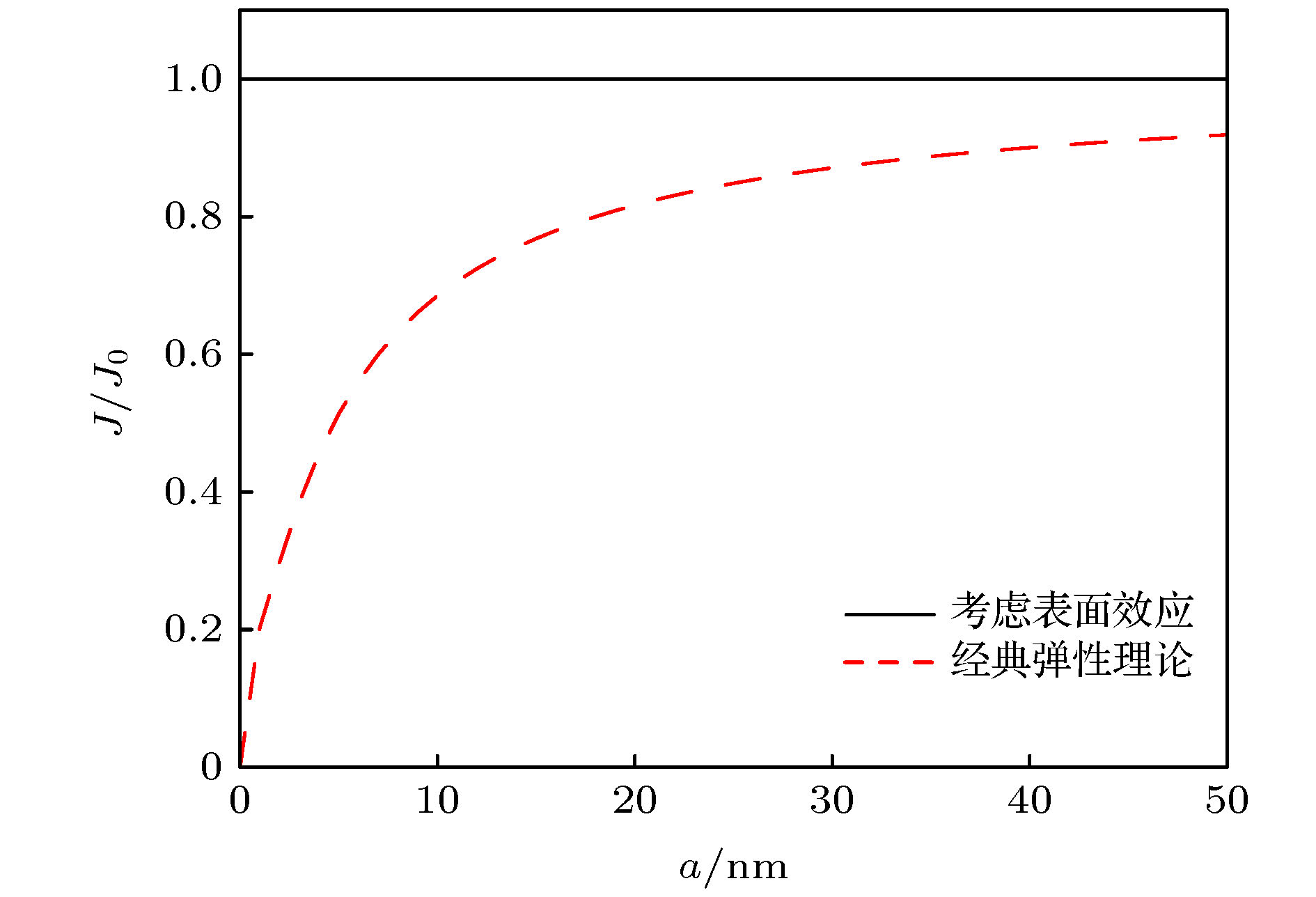
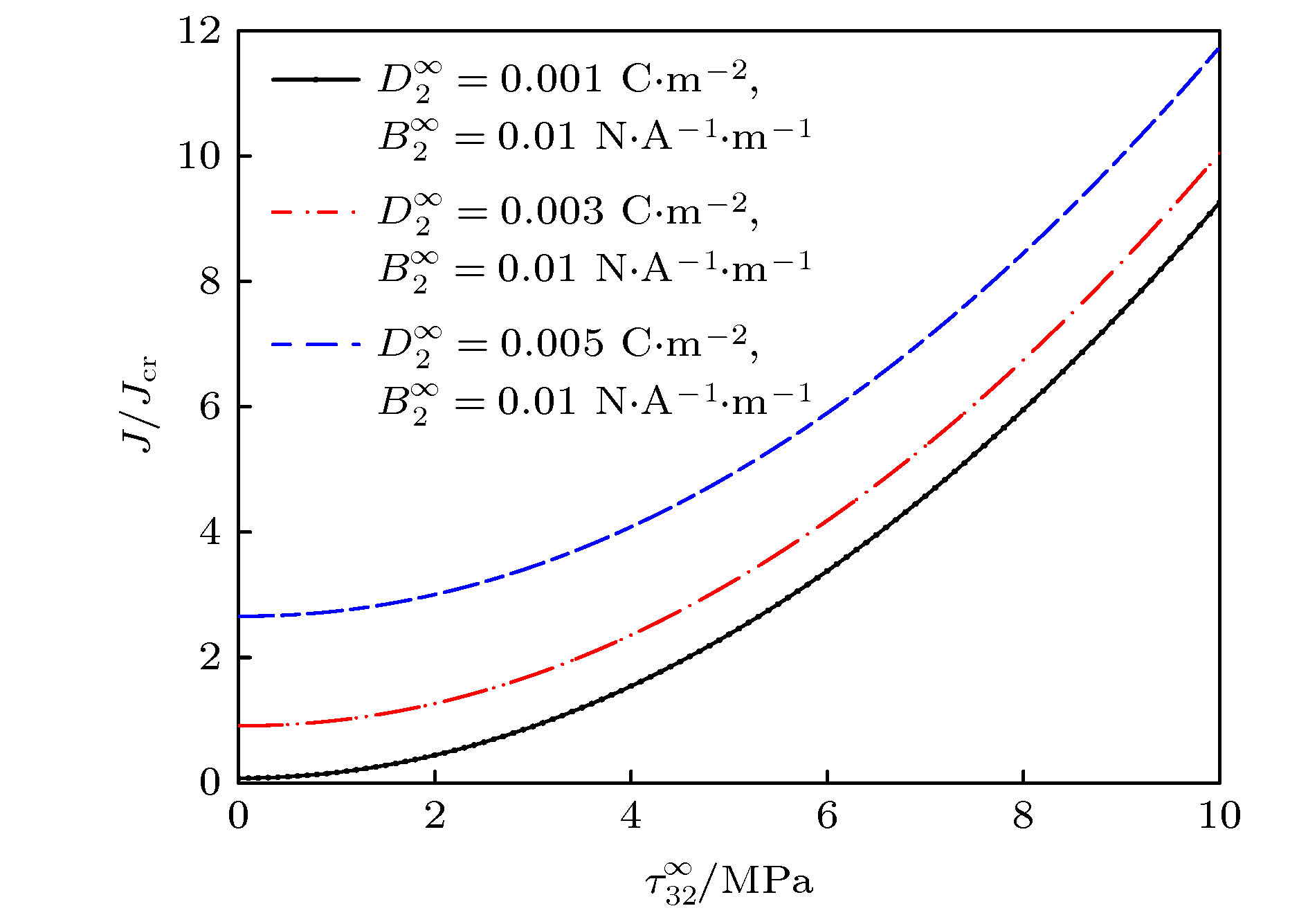
-
According to the conformal mapping from the exterior region of the regular n-polygon hole to the exterior region of a unit circle and from the exterior region of four cracks emanating from a circle to the interior region of a unit circle, a new conformal mapping is constructed to map the exterior region of four cracks emanating from a regular 4n-polygon hole to the interior of a unit circle. Then, based on the Gurtin-Murdoch surface/interface model and complex method, the anti-plane fracture of four nano-cracks emanating from a regular 4n-polygon nano-hole in magnetoelectroelastic material is studied. The exact solutions of stress intensity factor, electric displacement intensity factor, magnetic induction intensity factor, and energy release rate are obtained under the boundary condition of magnetoelectrically impermeable with considering the surface effect. Without considering the effect of the surface effect, the exact solution of four cracks emanating from a regular 4n-polygon hole in a magnetoelectroelastic material can be obtained. The numerical results show the influences of surface effect and the size of defect on the stress intensity factor, electric displacement intensity factor, magnetic induction intensity factor and energy release rate under the magnetoelectrically impermeable boundary condition. It can be seen that the stress intensity factor, electric displacement intensity factor, and magnetic induction intensity factor are significantly size-dependent when considering the surface effects of the nanoscale defects. And when the size of defect increases to a certain extent, the influence of surface effect begins to decrease and finally tends to follow the classical elasticity theory. When the distance between the center and the vertex of the regular 4n-polygon nano-hole is constant, the dimensionless field intensity factor decreases gradually with the increase of the number of edges, and approaches to the conclusion of a circular hole with four cracks. With the increase of the relative size of the crack, the dimensionless field intensity factor increases gradually. The dimensionless energy release rate of the nanoscale cracked hole has a significant size effect. The increase of mechanical load will increase the normalized energy release rate. The normalized energy release rate first decreases and then increases with electrical load increasing. The normalized energy release rate decreases with magnetic load increasing.
-
Keywords:
- magnetoelectroelastic materials /
- surface effect /
- nanoscale
[1] Nan C W 1994 Phys. Rev. B 50 6082
Google Scholar
[2] Guo J H, Lu Z X 2010 Int. J. solids Struct. 47 1847
Google Scholar
[3] Rogowski B 2011 Arch. Appl. Mech. 81 1607
Google Scholar
[4] 刘鑫, 郭俊宏, 于静 2016 内蒙古大学学报(自然科学版) 41 37
Google Scholar
Liu X, Guo J H, Yu J 2016 J. Inner Monglia Univ. (Natural Science Edition) 41 37
Google Scholar
[5] Gao C F, Kessler H, Balke H 2003 Int. J. Eng. Sci. 41 969
Google Scholar
[6] Gao C F, Kessler H, Balke H 2003 Int. J. Eng. Sci. 41 983
Google Scholar
[7] Liu X, Guo J H 2016 Theor. Appl. Fract. Mech. 86 225
Google Scholar
[8] 齐敏 2005 硕士学位论文 (石家庄: 石家庄铁道大学)
Qi M 2005 M. S. Thesis (Shijiazhuang: Shijiazhuang Tiedao University) (in Chinese)
[9] Lv X, Liu G T 2018 Chin. Phys. B 27 074601
Google Scholar
[10] Zhong X C, Li C F 2008 Arch. Appl. Mech. 78 117
Google Scholar
[11] Gurtin M E, Murdoch A I 1975 Arch. Ration. Mech. Anal. 57 291
Google Scholar
[12] Gurtin M E, Murdoch A I 1978 Int. J. Solids Struct. 14 431
Google Scholar
[13] Gurtin M E, Weissmuller J, Larche F 1998 Philos. Mag. A 78 1093
Google Scholar
[14] Xiao J H, XU Y L, Zhang F C 2018 Acta. Mech. 229 4915
Google Scholar
[15] 肖俊华, 崔友强, 徐耀玲, 张福成 2018 中国机械工程 29 2347
Google Scholar
Xiao J H, Cui Y Q, Xu Y L, Zhang F C 2018 China Mech. Eng. 29 2347
Google Scholar
[16] Xiao J H, Cui Y Q, Xu Y L, Zhang F C 2018 Theor. Appl. Fract. Mech. 96 476
Google Scholar
[17] Guo J H, Li X F 2018 Acta Mech. 229 4251
Google Scholar
[18] Liu Y Z, Guo J H, Zhang X Y 2019 Z. Angew. Math. Mech. 99 e201900043
[19] Guo J H, He L T, Liu Y Z, Li L H 2020 Theor. Appl. Fract. Mech. 107 102553
Google Scholar
[20] Guo J H, Lu Z X 2011 Appl. Math. Comput. 217 9397
Google Scholar
[21] 王永健 2012 博士学位论文 (南京: 南京航空航天大学)
Wang Y J 2012 Ph. D. Dissertation (Nanjing: Nanjing University of Aeronautics and Astronautics) (in Chinese)
[22] Fan S W, Guo J H, Yu J 2017 Chin. J. Aeronaut. 30 461
Google Scholar
[23] Dharmendra S, Sharma 2014 Int. J. Mech. Sci. 78 177
Google Scholar
[24] Wang Y B, Guo J H 2018 Appl. Math. Mech. -Engl. 39 797
Google Scholar
[25] Fang X Q, Gupta V, Liu J X 2013 Philos. Mag. Lett. 93 58
Google Scholar
[26] 穆斯海里什维里 著(赵惠元 译) 1958 数学弹性力学的几个基本问题 (北京: 科学出版社) 第233页
Muskhelishvili N I (translated by Zhao H Y) 1958 Some Basic Problems of the Mathematical Theory of Elasticity (Beijing: Science Press) p233 (in Chinese)
-
图 1 磁电弹性材料中含有带四条裂纹的正方形孔
Fig. 1. Four cracks emanating from a square hole in magnetoelectroelastic materials
图 3 只受机械载荷作用时表面效应对应力强度因子的影响
Fig. 3. Surface effect on the stress intensity factor near the crack tip induced by anti-plane mechanical load
$\tau_{32}^{\infty}$ only
图 4 只受电载荷作用时表面效应对应力强度因子的影响
Fig. 4. Surface effect on the stress intensity factor near the crack tip induced by in-plane electrical load
$D_2^{\infty}$ only
图 5 只受磁载荷作用时表面效应对应力强度因子的影响
Fig. 5. Surface effect on the stress intensity factor near the crack tip induced by in-plane magnetic load
$B_2^{\infty}$ only
图 6 只受机械荷作用时表面效应对电位移强度因子的影响
Fig. 6. Surface effect on the electric displacement intensity factor near the crack tip induced by anti-plane mechanical load
$\tau_{32}^{\infty}$ only
图 7 只受电载荷作用时表面效应对电位移强度因子的影响
Fig. 7. Surface effect on the electric displacement intensity factor near the crack tip induced by in-plane electrical load
$D_2^{\infty}$ only
图 8 只受磁载荷作用时表面效应对电位移强度因子的影响
Fig. 8. Surface effect on the electric displacement intensity factor near the crack tip induced by in-plane magnetic load
$B_2^{\infty}$ only
图 9 只受机械载荷作用时表面效应对磁感应强度因子的影响
Fig. 9. Surface effect on the magnetic induction intensity factor near the crack tip induced by anti-plane mechanical load
$\tau_{32}^{\infty}$ only
图 10 只受电载荷作用时表面效应对磁感应强度因子的影响
Fig. 10. Surface effect on the magnetic induction intensity factor near the crack tip induced by in-plane electrical load
$D_2^{\infty}$ only
图 11 只受磁载荷作用时表面效应对磁感应强度因子的影响
Fig. 11. Surface effect on the magnetic induction intensity factor near the crack tip induced by in-plane magnetic load
$B_2^{\infty}$ only
图 12 无量纲应力强度因子随右侧裂纹长度变化
Fig. 12. Variations of the dimensionless stress intensity factor at crack tip with the crack length
$L_1$ 
图 13 无量纲应力强度因子随n的变化
Fig. 13. Variations of the dimensionless stress intensity factor at crack tip with n
图 14 无量纲能量释放率随孔口尺寸的变化
Fig. 14. Variations of the dimensionless energy release rate with the size of the cracked hole
图 15 正则化能量释放率随机械载荷的变化
Fig. 15. Variations of the normalized energy release rate with the applied mechanical load
图 16 正则化能量释放率随电载荷的变化
Fig. 16. Variations of the normalized energy release rate with the applied eletrical load
图 17 正则化能量释放率随磁载荷的变化
Fig. 17. Variations of the normalized energy release rate with the applied magnetic load
-
[1] Nan C W 1994 Phys. Rev. B 50 6082
Google Scholar
[2] Guo J H, Lu Z X 2010 Int. J. solids Struct. 47 1847
Google Scholar
[3] Rogowski B 2011 Arch. Appl. Mech. 81 1607
Google Scholar
[4] 刘鑫, 郭俊宏, 于静 2016 内蒙古大学学报(自然科学版) 41 37
Google Scholar
Liu X, Guo J H, Yu J 2016 J. Inner Monglia Univ. (Natural Science Edition) 41 37
Google Scholar
[5] Gao C F, Kessler H, Balke H 2003 Int. J. Eng. Sci. 41 969
Google Scholar
[6] Gao C F, Kessler H, Balke H 2003 Int. J. Eng. Sci. 41 983
Google Scholar
[7] Liu X, Guo J H 2016 Theor. Appl. Fract. Mech. 86 225
Google Scholar
[8] 齐敏 2005 硕士学位论文 (石家庄: 石家庄铁道大学)
Qi M 2005 M. S. Thesis (Shijiazhuang: Shijiazhuang Tiedao University) (in Chinese)
[9] Lv X, Liu G T 2018 Chin. Phys. B 27 074601
Google Scholar
[10] Zhong X C, Li C F 2008 Arch. Appl. Mech. 78 117
Google Scholar
[11] Gurtin M E, Murdoch A I 1975 Arch. Ration. Mech. Anal. 57 291
Google Scholar
[12] Gurtin M E, Murdoch A I 1978 Int. J. Solids Struct. 14 431
Google Scholar
[13] Gurtin M E, Weissmuller J, Larche F 1998 Philos. Mag. A 78 1093
Google Scholar
[14] Xiao J H, XU Y L, Zhang F C 2018 Acta. Mech. 229 4915
Google Scholar
[15] 肖俊华, 崔友强, 徐耀玲, 张福成 2018 中国机械工程 29 2347
Google Scholar
Xiao J H, Cui Y Q, Xu Y L, Zhang F C 2018 China Mech. Eng. 29 2347
Google Scholar
[16] Xiao J H, Cui Y Q, Xu Y L, Zhang F C 2018 Theor. Appl. Fract. Mech. 96 476
Google Scholar
[17] Guo J H, Li X F 2018 Acta Mech. 229 4251
Google Scholar
[18] Liu Y Z, Guo J H, Zhang X Y 2019 Z. Angew. Math. Mech. 99 e201900043
[19] Guo J H, He L T, Liu Y Z, Li L H 2020 Theor. Appl. Fract. Mech. 107 102553
Google Scholar
[20] Guo J H, Lu Z X 2011 Appl. Math. Comput. 217 9397
Google Scholar
[21] 王永健 2012 博士学位论文 (南京: 南京航空航天大学)
Wang Y J 2012 Ph. D. Dissertation (Nanjing: Nanjing University of Aeronautics and Astronautics) (in Chinese)
[22] Fan S W, Guo J H, Yu J 2017 Chin. J. Aeronaut. 30 461
Google Scholar
[23] Dharmendra S, Sharma 2014 Int. J. Mech. Sci. 78 177
Google Scholar
[24] Wang Y B, Guo J H 2018 Appl. Math. Mech. -Engl. 39 797
Google Scholar
[25] Fang X Q, Gupta V, Liu J X 2013 Philos. Mag. Lett. 93 58
Google Scholar
[26] 穆斯海里什维里 著(赵惠元 译) 1958 数学弹性力学的几个基本问题 (北京: 科学出版社) 第233页
Muskhelishvili N I (translated by Zhao H Y) 1958 Some Basic Problems of the Mathematical Theory of Elasticity (Beijing: Science Press) p233 (in Chinese)
-
[1] 肖东东, 谷林. 基元构筑的功能材料皮米尺度结构. , 2023, 72(11): 116801. doi: 10.7498/aps.72.20230045 [2] 杨志平, 孔熙, 石发展, 杜江峰. 金刚石表面纳米尺度水分子的相变观测. , 2022, 71(6): 067601. doi: 10.7498/aps.71.20211348 [3] 陈小明, 李国荣. BaTiO3基无铅陶瓷大电致伸缩系数. , 2022, 71(16): 167701. doi: 10.7498/aps.71.20220451 [4] 尚帅朋, 陆勇俊, 王峰会. 表面效应对纳米线电极屈曲失稳的影响. , 2022, 71(3): 033101. doi: 10.7498/aps.71.20211864 [5] 杨志平, 孔熙, 石发展(Fazhan Shi), 杜江峰. 金刚石表面纳米尺度水分子的相变观测. , 2021, (): . doi: 10.7498/aps.70.20211348 [6] 张梦, 姚若河, 刘玉荣. 纳米尺度金属-氧化物半导体场效应晶体管沟道热噪声模型. , 2020, 69(5): 057101. doi: 10.7498/aps.69.20191512 [7] 梁晋洁, 高宁, 李玉红. 表面效应对铁 ${\left\langle 100 \right\rangle} $ 间隙型位错环的影响. , 2020, 69(3): 036101. doi: 10.7498/aps.69.20191379[8] 张烨, 张冉, 常青, 李桦. 壁面效应对纳米尺度气体流动的影响规律研究. , 2019, 68(12): 124702. doi: 10.7498/aps.68.20190248 [9] 彭劼扬, 王家海, 沈斌, 李浩亮, 孙昊明. 纳米颗粒的表面效应和电极颗粒间挤压作用对锂离子电池电压迟滞的影响. , 2019, 68(9): 090202. doi: 10.7498/aps.68.20182302 [10] 董杨, 杜博, 张少春, 陈向东, 孙方稳. 基于金刚石体系中氮-空位色心的固态量子传感. , 2018, 67(16): 160301. doi: 10.7498/aps.67.20180788 [11] 张龙艳, 徐进良, 雷俊鹏. 纳米尺度下气泡核化生长的分子动力学研究. , 2018, 67(23): 234702. doi: 10.7498/aps.67.20180993 [12] 李圣昆, 唐军, 毛宏庆, 王明焕, 陈国彬, 翟超, 张晓明, 石云波, 刘俊. Fe3O4纳米颗粒/聚二甲基硅氧烷复合材料磁电容效应的研究. , 2014, 63(5): 057501. doi: 10.7498/aps.63.057501 [13] 唐冬和, 杜磊, 王婷岚, 陈华, 陈文豪. 纳米尺度MOSFET过剩噪声的定性分析. , 2011, 60(10): 107201. doi: 10.7498/aps.60.107201 [14] 阳昌海, 文玉梅, 李 平, 卞雷祥. 偏置磁场对磁致伸缩/弹性/压电层合材料磁电效应的影响. , 2008, 57(11): 7292-7297. doi: 10.7498/aps.57.7292 [15] 张冬仙, 刘 超, 章海军. 微纳米尺度红外光热膨胀效应及新型光热驱动方法研究. , 2008, 57(5): 3107-3112. doi: 10.7498/aps.57.3107 [16] 罗文雄, 黄世华, 由芳田, 彭洪尚. YBO3:Eu3+纳米晶发光特性. , 2007, 56(3): 1765-1769. doi: 10.7498/aps.56.1765 [17] 田建辉, 韩 旭, 刘桂荣, 龙述尧, 秦金旗. SiC纳米杆的弛豫性能研究. , 2007, 56(2): 643-648. doi: 10.7498/aps.56.643 [18] 曾华荣, 余寒峰, 初瑞清, 李国荣, 殷庆瑞, 唐新桂. PZT铁电薄膜纳米尺度铁电畴的场致位移特性. , 2005, 54(3): 1437-1441. doi: 10.7498/aps.54.1437 [19] 都有为, 陈鹏, 朱建民, 邢定钰. 纳米结构ZnxFe3-xO4-α-Fe2O3多晶材料中的巨隧道磁电阻效应. , 2001, 50(11): 2275-2277. doi: 10.7498/aps.50.2275 [20] 于洪滨, 杨威生. 石墨上纳米尺度金岛的形成. , 1997, 46(3): 500-504. doi: 10.7498/aps.46.500
下载:
计量
- 文章访问数: 4632
- PDF下载量: 58
- 被引次数: 0
