-
在甚低频(3—30 kHz)及以下频段, 与波长相比, 传统天线属于电小辐射体, 因此辐射效率很低. 如果将永磁体进行机械旋转, 可以获得时变电磁场. 与传统天线相比, 旋转永磁体将机械能向电能转换, 不需要阻抗匹配网络, 提高了辐射效率. 为了计算旋转永磁体的电磁特性, 本文基于安培环路电流理论, 研究了空间正交磁偶极子与机械旋转永磁体的场等效关系. 在此基础上, 采用无限大空间并矢格林函数, 并引入旋转永磁体的初始旋转角参数, 推导了空间正交磁偶极子场分布的通用解析表达式, 作为分析旋转永磁体及其阵列的近场和远场分布的理论模型. 仿真表明, 当钕铁硼(NdFeB)永磁体剩余磁感应强度Br = 0.8 T、体积V = 270 cm3、转速为9600 r/min时, 对应频率为160 Hz, 在自由空间1 km的位置, 将产生15 fT的磁场; 在海水介质中, 当传输距离为250 m时, 磁场快速衰减到1 fT. 本文提出采用旋转永磁体阵列对近场分布特性进行调控, 仿真结果表明: 将两个相同的旋转永磁体组成二元阵, 将使近区磁感应强度提高3 dB; 改变阵元距离和初始旋转角, 可改变近区磁场分布方向图. 机械旋转永磁体为实现小型超低频发射天线提供了新的解决思路.Long wavelength results in the low radiation efficiency of a portable conventional antenna operating at very low frequency (VLF) and below. This has motivated one to develop an innovative approach to design an electrically small antenna in a frequency band lower than VLF. The time-varying electromagnetic fields can be generated by spinning a permanent magnet. In this way, the mechanical energy is converted to the electromagnetic energy, and the impedance matching networks with nonnegligible insertion loss are not required. Therefore, this mechanical antenna with spinning magnet can improve radiation efficiency in a low frequency band. In this paper, we give the detailed analysis procedure for the spinning magnet, which is seldom discussed in other published reports. In order to analyze the electromagnetic characteristics of the spinning magnet, in this paper we use the ampere return circuit theorem to investigate the equivalent relation between a spinning magnet and the orthogonal magnetic dipole. We introduce an initial spinning angle of the magnet into the dyadic green’s function. With this modification, we provide the rigorous analytic formula for field computation of the orthogonal magnetic dipole. Thus the electromagnetic characteristics of the spinning magnet and spinning magnet array can also be analyzed. For a spinning NdFeB magnet with a magnetization of Br = 0.8 T and a volume of Vr = 270 cm3 as well as 9600 revolutions per minute, the simulation results reveal that the magnetic field of 15 fT at 1 km in air space can be obtained. But the magnetic field of the spinning magnet decreases quickly to 1 fT at 250 m in sea water. Considering the potential demand for increasing the field strength in the near field region, we recommend to use a magnet array with small-sized elements. The magnet array can be used to control the near field pattern. We take two magnets as an example for studying the performance. It can be found from the simulation results that the magnetic near field is increased by 3 dB with the linear magnet array consisting of two elements. With the initial spinning angle of the magnet element adjusted, the near field pattern of the magnet array can be controlled. This is analogous to beam steering of traditional phased array for high band operation. It can be concluded from our study that the spinning magnet is a possible alternative solution for low frequency small transmitter antenna.
-
Keywords:
- mechanical antenna /
- permanent magnet /
- magnetic dipole /
- dyadic green function
[1] Madanayake A, Choi S, Tarek M, Dharmasena S, Mandal S, Glickstein J, Sehirlioglu A 2017 Moratuwa Engineering Research Conference Moratuwa, Sri Lanka, May 29−31, 2017 p230
[2] Sinha D, Amaratunga G A 2015 Phys. Rev. Lett. 114 147701
Google Scholar
[3] Nan T, Lin H, Gao Y, Matyushov A, Yu G, Chen H, Sun N, Wei S, Wang Z, Li M, Wang X, Belkessam A, Guo R, Chen B, Zhou J, Qian Z, Hui Y, Rinaldi M, McConney M E, Howe B M, Hu Z, Jones J G, Brown G J, Sun N X 2017 Nat. Commun. 8 296
Google Scholar
[4] Yao Z, Wang Y X E, Keller S, Carman G P 2015 IEEE Trans. Antennas Propag. 63 3335
Google Scholar
[5] 杨娜娜, 陈轩, 汪饶进 2018 67 157508
Google Scholar
Yang N N, Chen X, Wang R J 2018 Acta Phys. Sin. 67 157508
Google Scholar
[6] 俞斌, 胡忠强, 程宇心, 彭斌, 周子尧, 刘明 2018 67 157507
Google Scholar
Yu B, Hu Z Q, Chen Y X, Beng B, Zhou Z R, Liu M 2018 Acta Phys. Sin. 67 157507
Google Scholar
[7] 丁宏 2017 现代军事 4 71
Ding H 2017 Modern Military 4 71
[8] Gołkowski M, Park J, Bittle J, Babaiahgari B, Rorrer R A L, Celinski Z 2018 IEEE Symposium on Antennas and Propagation, Boston, MA, USA, July 8−13, 2018, p65
[9] Strachen N D, Booske J H, Behdad N 2018 IEEE Symposium on Antennas and Propagation, Boston, MA, USA, July 8−13, 2018, p67
[10] Barani N, Sarabandi K 2018 IEEE Symposium on Antennas and Propagation Boston, MA, USA, July 8−13, 2018 p95
[11] Bickford J A, McNabb R S, Ward P A, Freeman D K, Weinberg M S 2017 IEEE Symposium on Antennas and Propagation San Diego, CA, USA, July 9−14, 2017 p1475
[12] Zheng H, Zhao J B, Xiang B, Xiong Q P, Deng F S 2018 IEEE Symposium on Antennas and Propagation Boston, MA, USA, July 8−13, 2018 p751
[13] Manteghi M 2017 IEEE Symposium on Antennas and Propagation San Diego, CA, USA, July 9−14, 2017 p1997
[14] Gong S H, Liu Y, Liu Y 2018 Prog. Electromagn. Res. M 72 125
[15] Selvin S, Prasad M N S, Huang Y K, Wang E 2017 IEEE Symposium on Antennas and Propagation San Diego, CA, USA, July 9−14, 2017 p1477
[16] Prasad M N S, Selvin S, Tok R U, Huang Y K, Wang Y X 2018 IEEE Radio and Wireless Symposium (RWS) Anaheim, CA, USA, January 15−18, 2018 p171
[17] Prasad M N S 2017 M. S. Thesis (Los Angeles: University of California)
[18] 刘宏娟 2006 硕士学位论文 (北京: 北京工业大学)
Liu H J 2006 M. S. Thesis (Beijing: Beijing University of Technology) (in Chinese)
[19] 田录林, 贾嵘, 杨国清, 田琦, 李知航, 李辉 2008 电工技术学报 23 7
Google Scholar
Tian L L, Jia R, Yang G Q, Tian Q, Li Z H, Li H 2008 Journal of Electrical Engineer 23 7
Google Scholar
[20] 刘奇瑞 2010 硕士学位论文 (镇江: 江苏大学)
Wang Q R 2010 M. S. Thesis (Zhengjiang: Jiangsu University) (in Chinese)
[21] 毕德显 1985 电磁场理论 (北京: 电子工业出版社) 第355, 356页
Bi D X 1985 Electromagnetic Theory (Beijing: Publishing House of Electronics Industry) pp355, 356 (in Chinese)
[22] 金建铭 著 (尹家贤 译) 2017 高等电磁场理论 (第二版) (北京: 电子工业出版社) 第45页
Jin J M (translated by Yin J X) 2017 Theory and Computation of Electromagnetic Fields (Beijing: Publishing House of Electronics Industry) pp45 (in Chinese)
-
图 1 永磁体和等效磁偶极子坐标示意图 (a) 永磁体; (b) 电流环(磁偶极子)
Fig. 1. Schematic illustration of permanent magnet and equivalent magnetic dipole: (a) Permanent magnet; (b) equivalent magnetic dipole.
图 2 |Bz|随距离的变化(矩形永磁体和理想磁偶极子) (a) y = 0, z = 0, 沿x轴变化; (b) x = 0, z = 160 mm, 沿y轴变化; (c) x = 0, y = 0, 沿z轴变化; (d) x = 0, y = 180 mm, 沿z轴变化
Fig. 2. Variation of |Bz| versus distance (rectangular permanent magnet and ideal magnetic dipole): (a) y = 0, z = 0, along x-axis; (b) x = 0, z = 160 mm, along y-axis; (c) x = 0, y = 0, along z-axis; (d) x = 0, y = 180 mm, along z-axis.
图 3 旋转永磁体与旋转磁偶极子的等效 (a) 旋转永磁体; (b) 旋转磁偶极子
Fig. 3. Schematic illustration of the equivalence between spinning permanent magnet and spinning magnetic dipole: (a) Spinning permanent magnet; (b) spinning magnetic dipole.
图 4 旋转磁偶极子与正交磁流元的等效关系 (a) 旋转磁偶极子; (b) 正交磁偶极子; (c) 正交磁流元
Fig. 4. Schematic illustration of the equivalence between spinning magnet dipole and orthogonal magnetic dipoles: (a) Spinning magnet dipole; (b) orthogonal magnetic dipoles; (c) orthogonal magnetic currents
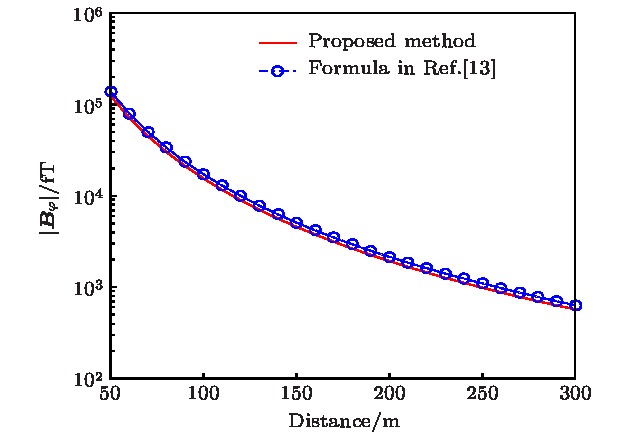
图 6 两种计算方法的结果对比(沿x轴, 球坐标变量为
$\varphi = {0^ \circ }$ ,$\theta = {90^ \circ }$ )Fig. 6. Results comparison between the proposed method and the formula in Ref. [13] (along x-axis, the spherical coordinate parameters:
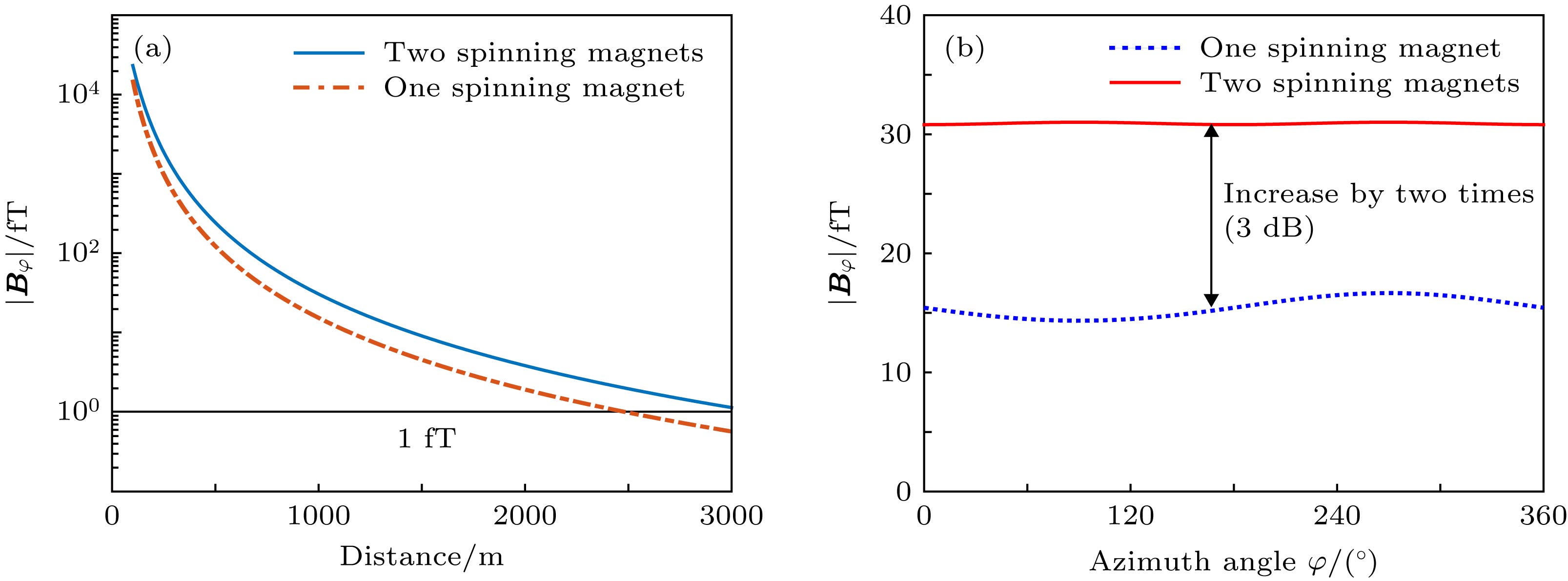
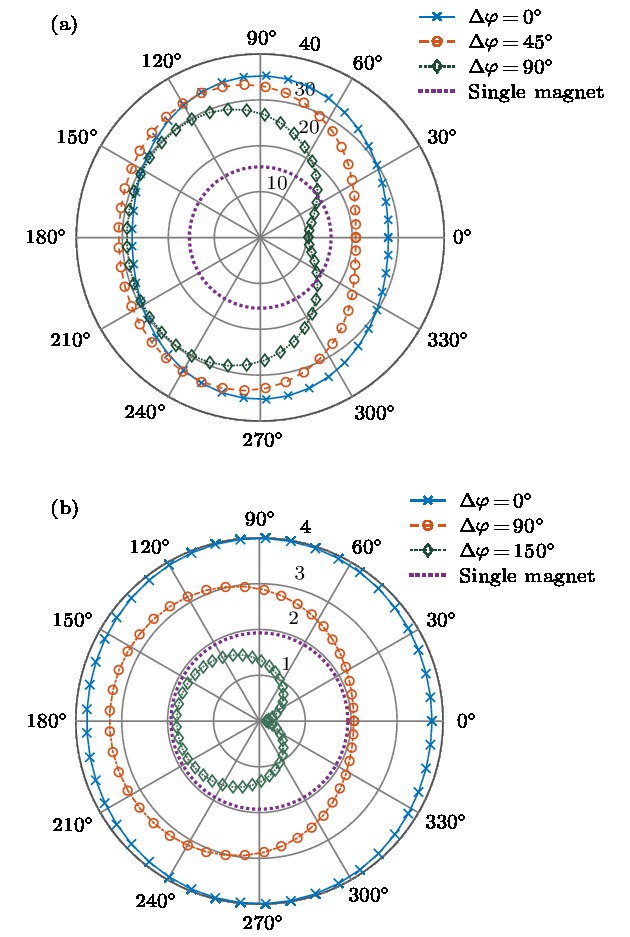
$\varphi = {0^ \circ }$ ,$\theta = {90^ \circ }$ ).
图 7 旋转永磁体的磁感应强度
$|{{ B}_\varphi }|$ 随距离的变化 (a) 空气; (b) 海水Fig. 7. Simulated magnetic flux density
$|{{ B}_\varphi }|$ versus distance: (a) Air; (b) seawater.
图 8 旋转永磁体磁感应强度的一般变化规律 (a) 160 Hz; (b) 海水
Fig. 8. Variation of simulated magnetic flux density
$|{{ B}_\varphi }|$ with material and frequency: (a) 160 Hz; (b) seawater.
图 10 二元旋转永磁体和单个旋转永磁体的场强对比 (a) 沿x轴, 球坐标变量为
$\varphi = {0^ \circ }$ ,$\theta = {90^ \circ }$ ; (b) 近场水平面方向图(d = 50 m, r = 1000 m,$ \Delta \varphi = {0^ \circ } $ )Fig. 10. Performance comparison between spinning magnet array and single spinning magnet: (a) Along x-axis, the spherical coordinate parameters
$ \varphi = {0^ \circ }$ ,$\theta = {90^ \circ } $ ; (b) magnetic near field pattern at the horizontal plane (d = 50 m, r = 1000m,$ \Delta \varphi ={0^ \circ }$ )
图 11 二元阵列俯仰面磁场分布
Fig. 11. Simulated magnetic flux density
$|{{ B}_\theta }|$ in the elevation plane.
图 12 改变初始旋转角, 二元阵列的水平面磁场方向图(a) r = 1000 m; (b) r = 2000 m
Fig. 12. Simulated magnetic flux density
$|{{ B}_\varphi }|$ of the spinning magnet array with two elements: (a) r = 1000 m; (b) r = 2000 m. -
[1] Madanayake A, Choi S, Tarek M, Dharmasena S, Mandal S, Glickstein J, Sehirlioglu A 2017 Moratuwa Engineering Research Conference Moratuwa, Sri Lanka, May 29−31, 2017 p230
[2] Sinha D, Amaratunga G A 2015 Phys. Rev. Lett. 114 147701
Google Scholar
[3] Nan T, Lin H, Gao Y, Matyushov A, Yu G, Chen H, Sun N, Wei S, Wang Z, Li M, Wang X, Belkessam A, Guo R, Chen B, Zhou J, Qian Z, Hui Y, Rinaldi M, McConney M E, Howe B M, Hu Z, Jones J G, Brown G J, Sun N X 2017 Nat. Commun. 8 296
Google Scholar
[4] Yao Z, Wang Y X E, Keller S, Carman G P 2015 IEEE Trans. Antennas Propag. 63 3335
Google Scholar
[5] 杨娜娜, 陈轩, 汪饶进 2018 67 157508
Google Scholar
Yang N N, Chen X, Wang R J 2018 Acta Phys. Sin. 67 157508
Google Scholar
[6] 俞斌, 胡忠强, 程宇心, 彭斌, 周子尧, 刘明 2018 67 157507
Google Scholar
Yu B, Hu Z Q, Chen Y X, Beng B, Zhou Z R, Liu M 2018 Acta Phys. Sin. 67 157507
Google Scholar
[7] 丁宏 2017 现代军事 4 71
Ding H 2017 Modern Military 4 71
[8] Gołkowski M, Park J, Bittle J, Babaiahgari B, Rorrer R A L, Celinski Z 2018 IEEE Symposium on Antennas and Propagation, Boston, MA, USA, July 8−13, 2018, p65
[9] Strachen N D, Booske J H, Behdad N 2018 IEEE Symposium on Antennas and Propagation, Boston, MA, USA, July 8−13, 2018, p67
[10] Barani N, Sarabandi K 2018 IEEE Symposium on Antennas and Propagation Boston, MA, USA, July 8−13, 2018 p95
[11] Bickford J A, McNabb R S, Ward P A, Freeman D K, Weinberg M S 2017 IEEE Symposium on Antennas and Propagation San Diego, CA, USA, July 9−14, 2017 p1475
[12] Zheng H, Zhao J B, Xiang B, Xiong Q P, Deng F S 2018 IEEE Symposium on Antennas and Propagation Boston, MA, USA, July 8−13, 2018 p751
[13] Manteghi M 2017 IEEE Symposium on Antennas and Propagation San Diego, CA, USA, July 9−14, 2017 p1997
[14] Gong S H, Liu Y, Liu Y 2018 Prog. Electromagn. Res. M 72 125
[15] Selvin S, Prasad M N S, Huang Y K, Wang E 2017 IEEE Symposium on Antennas and Propagation San Diego, CA, USA, July 9−14, 2017 p1477
[16] Prasad M N S, Selvin S, Tok R U, Huang Y K, Wang Y X 2018 IEEE Radio and Wireless Symposium (RWS) Anaheim, CA, USA, January 15−18, 2018 p171
[17] Prasad M N S 2017 M. S. Thesis (Los Angeles: University of California)
[18] 刘宏娟 2006 硕士学位论文 (北京: 北京工业大学)
Liu H J 2006 M. S. Thesis (Beijing: Beijing University of Technology) (in Chinese)
[19] 田录林, 贾嵘, 杨国清, 田琦, 李知航, 李辉 2008 电工技术学报 23 7
Google Scholar
Tian L L, Jia R, Yang G Q, Tian Q, Li Z H, Li H 2008 Journal of Electrical Engineer 23 7
Google Scholar
[20] 刘奇瑞 2010 硕士学位论文 (镇江: 江苏大学)
Wang Q R 2010 M. S. Thesis (Zhengjiang: Jiangsu University) (in Chinese)
[21] 毕德显 1985 电磁场理论 (北京: 电子工业出版社) 第355, 356页
Bi D X 1985 Electromagnetic Theory (Beijing: Publishing House of Electronics Industry) pp355, 356 (in Chinese)
[22] 金建铭 著 (尹家贤 译) 2017 高等电磁场理论 (第二版) (北京: 电子工业出版社) 第45页
Jin J M (translated by Yin J X) 2017 Theory and Computation of Electromagnetic Fields (Beijing: Publishing House of Electronics Industry) pp45 (in Chinese)
下载:
计量
- 文章访问数: 13170
- PDF下载量: 275
- 被引次数: 0
