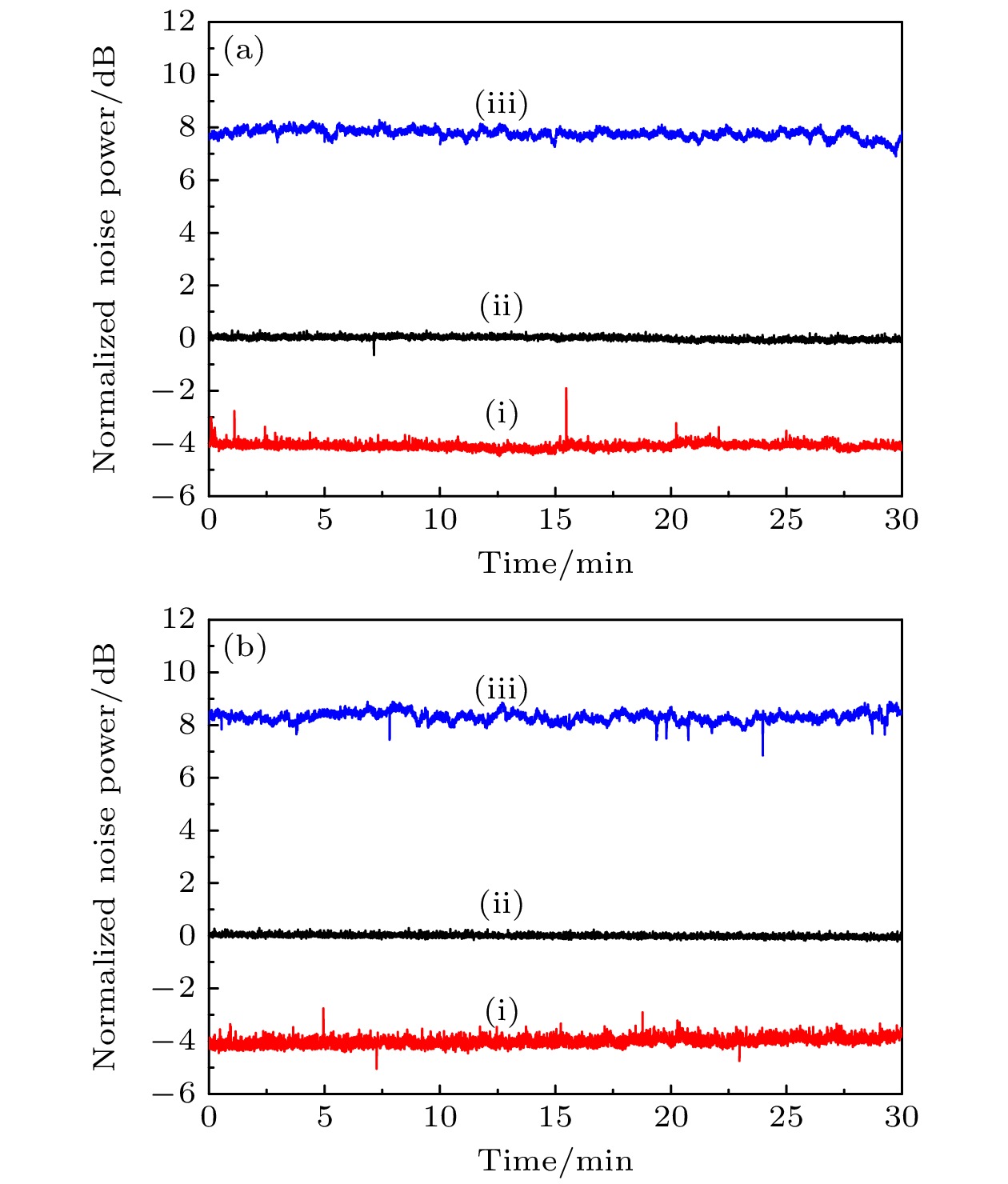
-
本文提出了利用单边带移频光实现非简并光学参量放大器相敏操控的方案, 实验研究了在对非简并光学参量放大器相敏操控过程中, 单边带移频光注入的方案和信号光注入的方案对产生的低频双模正交压缩真空态光场的影响. 实验结果表明, 信号光注入非简并光学参量放大器实现相敏操控过程中, 压缩真空态的压缩度随着注入信号光场功率的增加不断减小直至消失. 而在单边带移频光注入非简并光学参量放大器实现相敏操控过程中, 正交振幅和正交位相压缩真空态的压缩度对注入移频光场的功率变化都不敏感, 压缩度几乎不变. 采用单边带移频光方案实现稳定的相敏操控, 非简并光学参量放大器运转于相敏放大状态达30 min, 获得了稳定输出的低频双模正交压缩真空态光场, 在傅里叶分析频率为200 kHz测量的正交振幅分量的压缩度为(4.1±0.1) dB, 正交位相分量的压缩度为(4.0±0.2) dB.
Two-mode orthogonal squeezed vacuum states are an important quantum resource for quantum communication, quantum computing, quantum simulation, quantum precision measurement and sensing. It is essential to obtain stable two-mode orthogonal squeezed vacuum states in a low frequency range and compact configurations for practical applications, especially in quantum precision measurement and sensing. Two-mode orthogonal squeezed vacuum states are commonly produced via a subthreshold nondegenerate optical parametric amplifier (NOPA) in a continuous variable system. However, it is a difficult problem that the subthreshold NOPA cavity is phase sensitive manipulated to obtain stable squeezed vacuum states. Previous signal light injecting scheme relies on an injection of a weak light field into the subthreshold NOPA for phase sensitive manipulation. The injected signal light has the same frequency as the generated squeezed vacuum state. Thereby even the weakest injected signal light can introduce large amounts of excessive noise at low frequencies and the squeezing degree of two-mode squeezed vacuum states will be reduced or squeezing cannot be achieved. In this paper, a single sideband frequency shifted light injecting scheme is proposed for phase sensitive manipulation of NOPA. The comparison between the single sideband frequency shifted light injecting scheme and the signal light injecting scheme for realization of phase sensitive manipulation of NOPA is conducted. The effects of the two schemes on the generation of the low-frequency two-mode orthogonal squeezed vacuum state light field are investigated experimentally . The experimental results show that in the signal light injecting scheme for phase sensitive manipulation, the squeezing degree of the two-mode orthogonal squeezed vacuum state continuously decreases until it disappears as the power of injected signal light increases. In the process of phase sensitive manipulation of NOPA by using the single sideband frequency shifted light injecting scheme, the squeezing degree of the two-mode orthogonal squeezed vacuum state does not change with the power of the injected frequency shifted light increasing. Stable phase sensitive manipulation is realized by injecting single sideband frequency shifted light into NOPA. The NOPA is operated in a phase sensitive amplification state for 30 min. Stable low-frequency two-mode orthogonal squeezed vacuum states are obtained. The (4.1 ± 0.1) dB amplitude orthogonal squeezed vacuum states and (4.0 ± 0.2) dB phase orthogonal squeezed vacuum states at a frequency of 200 kHz are generated stably, in a compact NOPA configuration. -
Keywords:
- two-mode quadrature squeezed vacuum states /
- optical parametric amplifier /
- phase-sensitive manipulations
[1] Notarnicola M N, Olivares S 2023 Phys. Rev. A 108 022404
Google Scholar
[2] Cochrane P T, Ralph T C, Milburn G J 2002 Phys. Rev. A 65 062306
Google Scholar
[3] Seok H L, Hyunseok J 2019 Photonics Res. 7 A7
Google Scholar
[4] Ralph T C 2011 Phys. Rev. A 84 022339
Google Scholar
[5] Sabín C 2023 EPJ Quantum Technol. 10 4
Google Scholar
[6] Lawrie B J, Lett P D, Marino A M, Pooser R C 2019 ACS Photonics 6 1307
Google Scholar
[7] Ma Y Q, Miao H X, Pang B H, Evans M, Zhao C N, Harms J, Schnabel R, Chen Y B 2017 Nat. Phys. 13 776
Google Scholar
[8] 蔚娟, 张岩, 吴银花, 杨文海, 闫智辉, 贾晓军 2023 72 034202
Google Scholar
Yu J, Zhang Y, Wu Y H, Yang W H, Yan Z H, Jia X J 2023 Acta Phys. Sin. 72 034202
Google Scholar
[9] Furusawa A, Sørensen J L, Braunstein S L, Fuchs C A, Kimble H J, Polzik E S 1998 Science 282 706
Google Scholar
[10] Takei N, Yonezawa H, Aoki T, Furusawa A 2005 Phys. Rev. Lett. 94 220502
Google Scholar
[11] Su X L, Tan A H, Jia X J, Zhang J, Xie C D, Peng K C 2007 Phys. Rev. Lett. 98 070502
Google Scholar
[12] Su X L, Hao S H, Deng X W, Ma L Y, Wang M H, Jia X J, Xie C D, Peng K C 2013 Nat. Commun. 4 2828
Google Scholar
[13] Su X L, Tian C X, Deng X W, Li Q, Xie C D, Peng K C 2016 Phys. Rev. Lett. 117 240503
Google Scholar
[14] 周瑶瑶, 刘艳红, 闫智辉, 贾晓军 2021 70 104203
Google Scholar
Zhou Y Y, Liu Y H, Yan Z H, Jia X J 2021 Acta Phys. Sin. 70 104203
Google Scholar
[15] Ou Z Y, Pereira S F, Kimble H J 1992 Appl. Phys. B 55 265
Google Scholar
[16] Zhang Y, Su H, Xie C D, Peng K C 1999 Phys. Lett. A 259 171
Google Scholar
[17] Wang Y, Shen H, Jin X L, Su X L, Xie C D, Peng K C 2010 Opt. Express 18 6149
Google Scholar
[18] Yap M J , Altin P, McRae T G, Slagmolen B J J, Ward R L, McClelland D E 2019 Nat. Photonics 14 223
Google Scholar
[19] Bowen W P, Schnabel R, Lam P K, Ralph T C 2003 Phys. Rev. Lett. 90 043601
Google Scholar
[20] Bowen W P, Schnabel R, Lam P K, Ralph T C 2004 Phys. Rev. A 69 012304
Google Scholar
[21] Zhang Y, Wang H, Li X Y, Jing J T, Xie C D, Peng K C 2000 Phys. Rev. A 62 023813
Google Scholar
[22] Zhang Y, Kasai K, Watanabe M 2002 Phys. Lett. A 297 29
Google Scholar
[23] McKenzie K, Grosse N, Bowen W P, Whitcomb S E, Gray M B, McClelland D E, Lam P K 2004 Phys. Rev. Lett. 93 161105
Google Scholar
[24] Shang Y N, Yan Z H, Jia X J, Su X L, Xie C D 2011 Chin. Phys. B 20 034209
Google Scholar
[25] Su X L 2013 Chin. Phys. B 22 080304
Google Scholar
[26] Vahlbruch H, Chelkowski S, Hage B, Franzen A, Danzmann K, Schnabel R 2006 Phys. Rev. Lett. 97 011101
Google Scholar
[27] Eberle T, Händchen V, Schnabel R 2013 Opt. Express 21 11546
Google Scholar
[28] Zhang W H, Jiao N J, Li R X, Tian L, Wang Y J, Zheng Y H 2021 Opt. Express 29 24315
Google Scholar
[29] Wang X B, Hiroshima T, Tomita A, Hayashi M 2007 Phys. Rep. 448 1
Google Scholar
-
图 1 移频光场在双模压缩真空态产生过程中的光场变化示意图
Fig. 1. Schematic diagram of frequency shifted light field changes during the generation of dual mode squeezed states.
图 2 移频技术实现NOPA相敏操控并产生稳定输出的低频双模正交压缩真空态光场
Fig. 2. Manipulation of phase sensitive in NOPA and generation of stable output low frequency two mode orthogonal squeezed vacuum states using frequency shift technology.
图 3 测量的双模正交压缩真空态的噪声功率随注入光场功率的变化
Fig. 3. Measured noise powers of two mode quadrature squeezed vacuum states vesus power of injected light field.
图 4 傅里叶分析频率为200 kHz处测得双模正交压缩真空态的噪声功率 (a) 正交振幅压缩真空态; (b) 正交位相压缩真空态
Fig. 4. Measured noise powers of two-mode quadrature squeezed vacuum states at Fourier analysis frequency of 200 kHz: (a) Amplitude quadrature squeezed vacuum states; (b) phase quadrature squeezed vacuum states.
-
[1] Notarnicola M N, Olivares S 2023 Phys. Rev. A 108 022404
Google Scholar
[2] Cochrane P T, Ralph T C, Milburn G J 2002 Phys. Rev. A 65 062306
Google Scholar
[3] Seok H L, Hyunseok J 2019 Photonics Res. 7 A7
Google Scholar
[4] Ralph T C 2011 Phys. Rev. A 84 022339
Google Scholar
[5] Sabín C 2023 EPJ Quantum Technol. 10 4
Google Scholar
[6] Lawrie B J, Lett P D, Marino A M, Pooser R C 2019 ACS Photonics 6 1307
Google Scholar
[7] Ma Y Q, Miao H X, Pang B H, Evans M, Zhao C N, Harms J, Schnabel R, Chen Y B 2017 Nat. Phys. 13 776
Google Scholar
[8] 蔚娟, 张岩, 吴银花, 杨文海, 闫智辉, 贾晓军 2023 72 034202
Google Scholar
Yu J, Zhang Y, Wu Y H, Yang W H, Yan Z H, Jia X J 2023 Acta Phys. Sin. 72 034202
Google Scholar
[9] Furusawa A, Sørensen J L, Braunstein S L, Fuchs C A, Kimble H J, Polzik E S 1998 Science 282 706
Google Scholar
[10] Takei N, Yonezawa H, Aoki T, Furusawa A 2005 Phys. Rev. Lett. 94 220502
Google Scholar
[11] Su X L, Tan A H, Jia X J, Zhang J, Xie C D, Peng K C 2007 Phys. Rev. Lett. 98 070502
Google Scholar
[12] Su X L, Hao S H, Deng X W, Ma L Y, Wang M H, Jia X J, Xie C D, Peng K C 2013 Nat. Commun. 4 2828
Google Scholar
[13] Su X L, Tian C X, Deng X W, Li Q, Xie C D, Peng K C 2016 Phys. Rev. Lett. 117 240503
Google Scholar
[14] 周瑶瑶, 刘艳红, 闫智辉, 贾晓军 2021 70 104203
Google Scholar
Zhou Y Y, Liu Y H, Yan Z H, Jia X J 2021 Acta Phys. Sin. 70 104203
Google Scholar
[15] Ou Z Y, Pereira S F, Kimble H J 1992 Appl. Phys. B 55 265
Google Scholar
[16] Zhang Y, Su H, Xie C D, Peng K C 1999 Phys. Lett. A 259 171
Google Scholar
[17] Wang Y, Shen H, Jin X L, Su X L, Xie C D, Peng K C 2010 Opt. Express 18 6149
Google Scholar
[18] Yap M J , Altin P, McRae T G, Slagmolen B J J, Ward R L, McClelland D E 2019 Nat. Photonics 14 223
Google Scholar
[19] Bowen W P, Schnabel R, Lam P K, Ralph T C 2003 Phys. Rev. Lett. 90 043601
Google Scholar
[20] Bowen W P, Schnabel R, Lam P K, Ralph T C 2004 Phys. Rev. A 69 012304
Google Scholar
[21] Zhang Y, Wang H, Li X Y, Jing J T, Xie C D, Peng K C 2000 Phys. Rev. A 62 023813
Google Scholar
[22] Zhang Y, Kasai K, Watanabe M 2002 Phys. Lett. A 297 29
Google Scholar
[23] McKenzie K, Grosse N, Bowen W P, Whitcomb S E, Gray M B, McClelland D E, Lam P K 2004 Phys. Rev. Lett. 93 161105
Google Scholar
[24] Shang Y N, Yan Z H, Jia X J, Su X L, Xie C D 2011 Chin. Phys. B 20 034209
Google Scholar
[25] Su X L 2013 Chin. Phys. B 22 080304
Google Scholar
[26] Vahlbruch H, Chelkowski S, Hage B, Franzen A, Danzmann K, Schnabel R 2006 Phys. Rev. Lett. 97 011101
Google Scholar
[27] Eberle T, Händchen V, Schnabel R 2013 Opt. Express 21 11546
Google Scholar
[28] Zhang W H, Jiao N J, Li R X, Tian L, Wang Y J, Zheng Y H 2021 Opt. Express 29 24315
Google Scholar
[29] Wang X B, Hiroshima T, Tomita A, Hayashi M 2007 Phys. Rep. 448 1
Google Scholar
下载:
计量
- 文章访问数: 2198
- PDF下载量: 63
- 被引次数: 0
