-
超表面是由亚波长单元组成控制电磁波的人工结构, 研究发现通过对其进行编码排列可实现对电磁波能量的任意控制. 本文利用四种形状相同、尺寸不同的人字形结构单元, 结合其不同相位响应和不同的相位灵敏度设计了太赫兹频率编码器, 通过进行特定编码, 在频率改变的情况下, 实现了对电磁波能量辐射调控. 分别设计了1-bit, 2-bit周期和非周期太赫兹频率编码器, 通过数值计算和仿真模拟验证了上述特性, 而且该结构对太赫兹波辐射主瓣能量有很好的分散作用, 可以有效减少雷达散射截面, 雷达散射截面缩减在θ = 0, φ = 0方向上最大可达29 dB, 在太赫兹波隐身中具有巨大应用价值.Metasurface is an artificial structure composed of sub-wavelength units which can realize the arbitrary control of electromagnetic wave energy by coding and arranging metasurface. Unlike the previous coding metasurface with a fixed phase difference of the neighbor coding unit cells, the frequency coding metasurface possesses the main feature that it has the linear change phase difference and different phase sensitivities in the whole working frequency band of the digital unit cells. And it can flexibly control the reflected terahertz waves to the numerous directions by changing the working frequency without redesigning the coding metasurface structure. In this paper, the frequency coding metasurfaces are designed by using four herringbone unit cells with the same shape and different sizes. They have the same phase response at the initial frequency and the different phase sensitivities throughout the frequency band. To describe the frequency coding characteristics of the unit cells, the digital numbers "0" and "1" are used to represent the low phase sensitivity and high phase sensitivity, respectively. Using the frequency digital coding, it can control the electromagnetic wave energy radiations by a single digital coding metasurface without changing the spatial coding pattern. By the combination of the spatial coding and frequency coding, It can manipulate the electromagnetic wave energy radiations more flexibly. We demonstrate 1-bit, 2-bit periodic frequency coding metasurfaces and 2-bit non-periodic frequency coding metasurface. They are all designed in the pre-designed coding sequence to control the electromagnetic wave energy radiations. Numerically simulated results confirm that the frequency coding metasurface can flexibly control the reflected terahertz waves to the numerous directions by changing the working frequency without redesigning the coding metasurface structure. Additionally, the number of the backward diffusion-like scattering beam increases with the change of frequency for the 2-bit random terahertz frequency coding metasurface. It has a good dispersion effect on the main lobe energy of terahertz wave radiation. The radar cross section can be reduced effectively, and the maximum value of radar cross section reduction can reach 29 dB in the direction of θ = 0, φ = 0. It has a great application value in the terahertz wave cloaking.
-
Keywords:
- coding metasurface /
- terahertz manipulation /
- phase sensitivity
[1] Yu N F, Genevet P, Kats M A, Aieta F, Tetienne P J, Capasso F, Gaburro Z 2011 Science 334 333
Google Scholar
[2] Yu N F,Capasso F 2014 Nat. Mater. 13 139
Google Scholar
[3] Liu L X, Zhang X Q, Kenney M, Su X Q, Xu N N, Ouyang C M, Shi Y L, Han J G, Zhang W L, Zhang S 2014 Adv. Mater. 26 5031
Google Scholar
[4] Li Y F, Zhang J Q, Qu S B, Wang J F, Chen H Y, Xu Z, Zhang A X 2014 J. Appl. Phys. 115 063908
Google Scholar
[5] Yu Y F, Zhu A Y, Paniagua-Domínguez R, Fu Y H, Luk'Yanchuk B, Kuznetsov A I 2015 Laser Photon. Rev. 9 412
Google Scholar
[6] Li Y F, Zhang J Q, Qu S B, Wang J F, Zheng L, Pang Y Q, Xu Z, Zheng A X 2015 J. Appl. Phys. 117 044501
Google Scholar
[7] Zhu H F, Semperlotti F 2016 Phys. Rev. Lett. 117 034302
Google Scholar
[8] Wang L, Kruk S, Tang H Z, Li T, Kravchenko I, Neshev D N, Kivshar Y S 2016 Optica 3 1504
Google Scholar
[9] Li Y F, Zhang J Q, Qu S B, Wang J F, Chen H Y, Xu Z, Zhang A X 2014 Appl. Phys. Lett. 104 221110
Google Scholar
[10] Ramli M N, Ping J S, Jamlos M F, Lago H, Aziz N M, Al-Hadi A A 2017 Appl. Phys. A 123 149
Google Scholar
[11] Xu H X, Wang G M, Liang J G, Qi M Q, Gao X 2013 IEEE Trans. Antennas Propag. 61 3442
Google Scholar
[12] Wan X, Shen X P, Luo Y, Cui T J 2014 Laser Photon. Rev. 8 757
Google Scholar
[13] Li Z L, Kim I, Zhang L, Mehmood M Q, Anwar M S, Saleem M, Lee D, Nam K T, Zhang S, Luk'Yanchuk B, Wang Y, Zheng G X, Rho J, Qiu C W 2017A CS Nano 11 9382
Google Scholar
[14] Cui TJ, Liu S, Li L L 2016 Light Sci. Appl. 5 e16172
Google Scholar
[15] Huang C, Sun B, Pan W B, Cui J H, Wu X Y, Luo X G 2017 Sci. Rep. 7 42302
Google Scholar
[16] Li J S, Zhao Z J, Yao J Q 2017 Opt. Express 25 29983
Google Scholar
[17] Cui T J, Liu S 2017 Adv. Opt. Mater. 5 1700624
Google Scholar
[18] Li L L, Cui T J, Ji W, Liu S, Ding J, Wan X, Li Y B, Jiang M H, Qiu C W, Zhang S 2017 Nat. Commun. 8 197
Google Scholar
[19] Su J X, Cui Y Y, Li Z R, Yan Q L, Che Y X, Yin H C 2018 AIP Adv. 8 035027
Google Scholar
[20] Li J S, Yao J Q 2018 IEEE Photon. J. 10 1
Google Scholar
-
图 1 人字形超表面单元结构 (a)单元结构三维立体图; (b)单元结构二维平面图
Fig. 1. Herringbone metasurfaceunit structure: (a) Three-dimensional of unit structure; (b) two-simensional of unit structure.
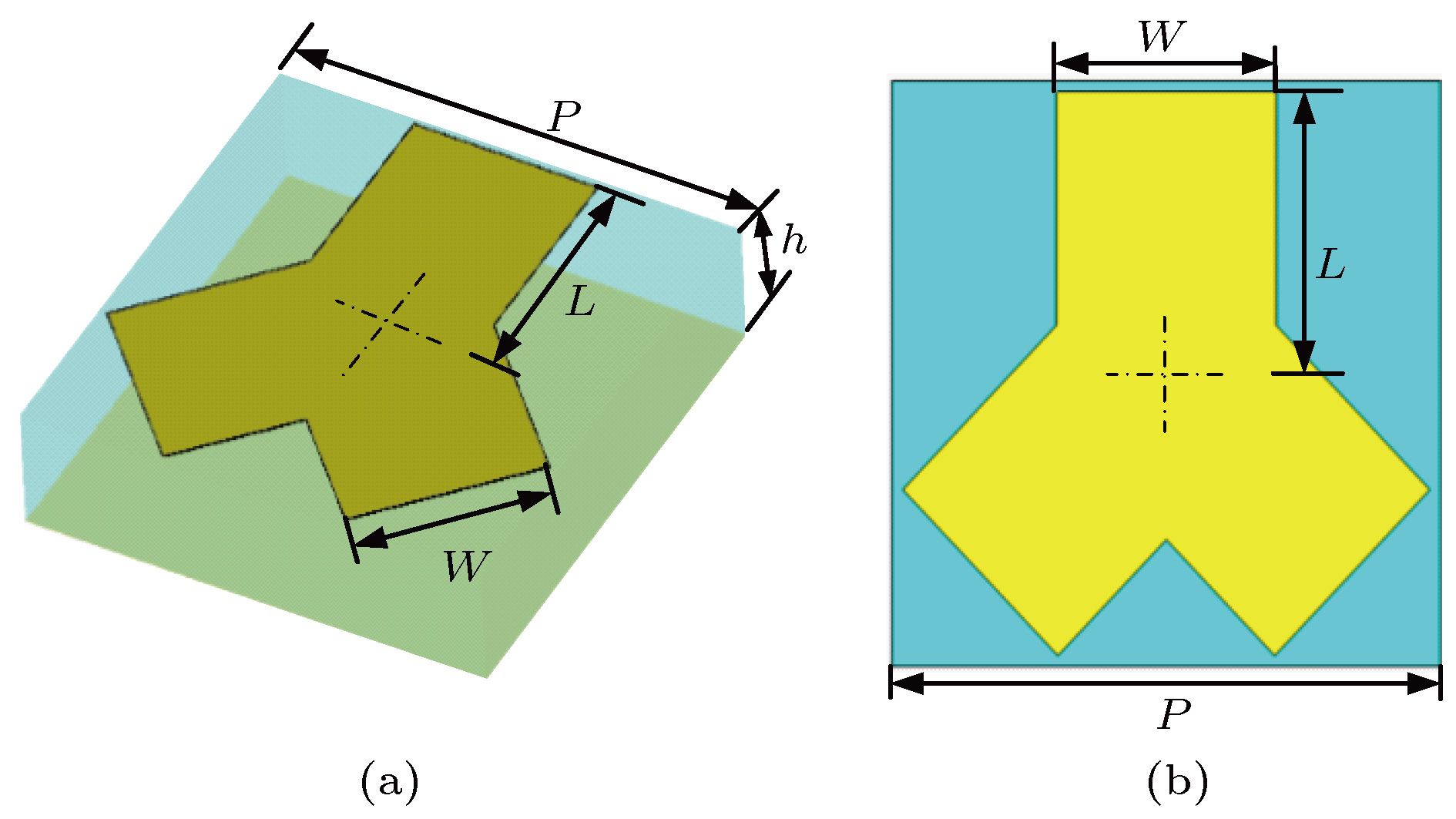
图 2 4种人字形超表面基本单元结构及其特性曲线 (a) A单元(L = 48 μm); (b) B单元(L = 40 μm); (c) C单元(L = 34 μm); (d) D单元(L = 20 μm); (e) 4种单元在0.4 THz到1.0 THz下的反射率; (f) 4种单元在0.4 THz到1.0 THz下的反射相位
Fig. 2. The basic unit structure and characteristic curves of four kinds of herringbone metasurface: (a) Unit A (L = 48 μm); (b) unit B (L = 40 μm); (c) unit C (L = 34 μm); (d) unit D (L = 20 μm); (e) reflectivity of four unitsfrom 0.4 THz to 1.0 THz; (f) reflection phase of four units from 0.4 THz to 1.0 THz.
图 3 太赫兹频率编码器 (a)以“0-0, 0-1, 0-0, 0-1”序列沿x方向排列1-bit周期太赫兹频率编码器; (b)棋盘式1-bit周期太赫兹频率编码器; (c)以“00-00, 00-01, 00-10, 00-11”序列沿x方向排列2-bit周期太赫兹频率编码器; (d) 2-bit随机太赫兹频率编码器; (e) 2-bit非周期太赫兹频率编码器
Fig. 3. The terahertz frequency coding metasurface: (a) 1-bit periodic terahertz frequency coding metasurface arranged along x direction with “0-0, 0-1, 0-0, 0-1” sequence; (b) chessboard 1-bit periodic terahertz frequency coding metasurface; (c) 2-bit periodic terahertz frequency coding metasurface arranged along x direction with “00-00, 00-01, 00-10, 00-11” sequence; (d) 2-bit random terahertz frequency coding metasurface; (e) 2-bit non-periodic terahertz frequency coding metasurface.
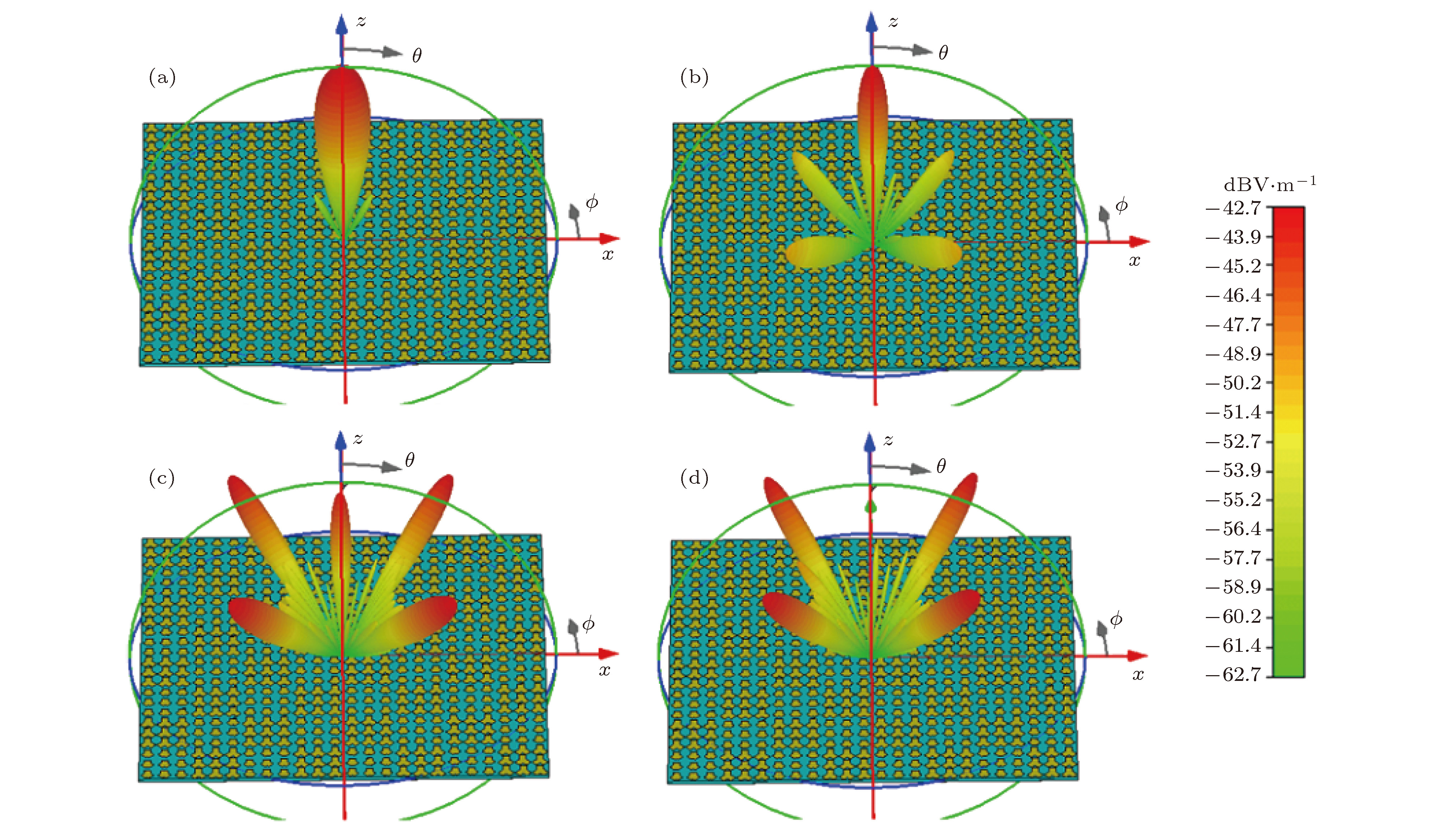
图 4 序列“0-0, 0-1, 0-0, 0-1”沿x方向上周期排布的1-bit太赫兹频率编码器 (a) f = 0.4 THz, (b) f = 0.75 THz, (c) f = 0.95 THz, (d) f = 1.0 THz时的三维远场图
Fig. 4. 1-bit terahertz frequency coding metasurface arranged periodically along x direction with sequence “0-0,0-1, 0-0, 0-1”: Three-dimensional far-field pattern of (a) f = 0.4 THz, (b) f = 0.75 THz, (c) f = 0.95 THz, (d) f = 1.0 THz.
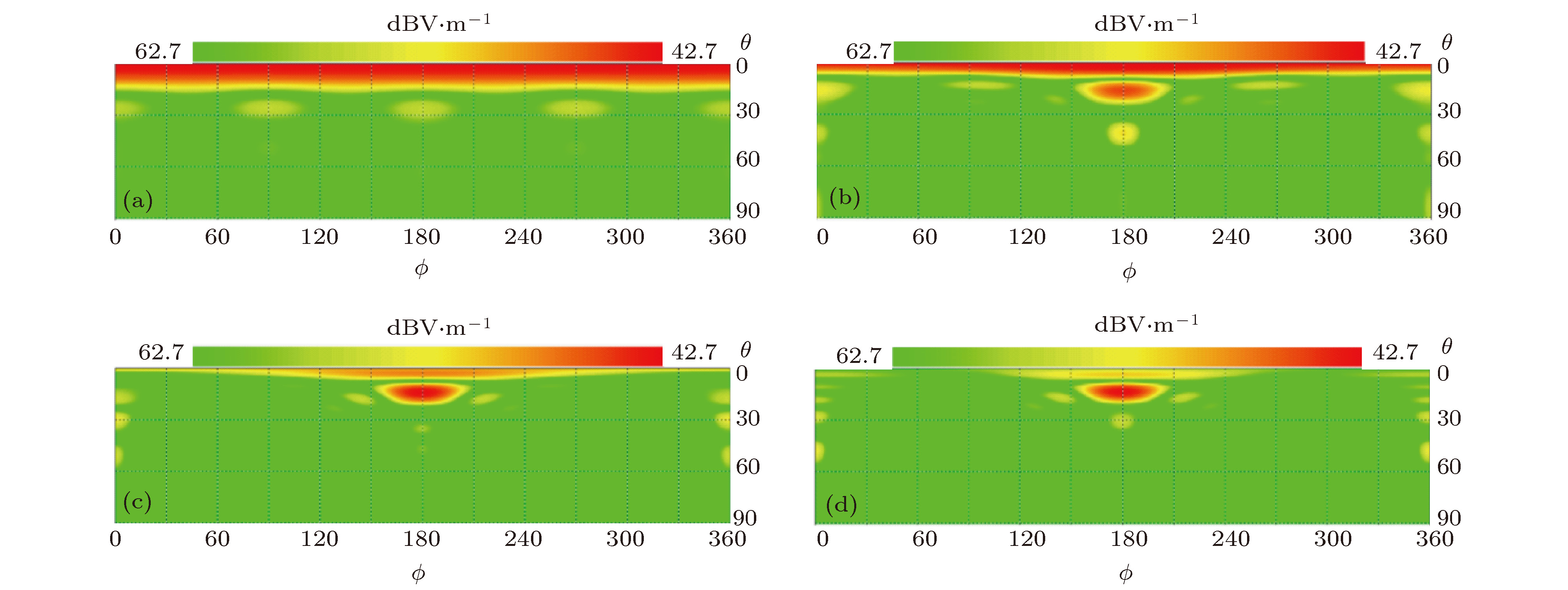
图 5 序列“0-0, 0-1, 0-0, 0-1”沿x方向上周期排布的1-bit太赫兹频率编码器 (a) f = 0.4 THz, (b) f = 0.75 THz, (c) f = 0.95 THz, (d) f = 1.0 THz时的二维电场图
Fig. 5. 1-bit terahertz frequency coding metasurface arranged periodically along x direction with sequence“0-0, 0-1, 0-0, 0-1”: Two-dimensional electric field pattern of (a) f = 0.4 THz, (b) f = 0.75 THz, (c) f = 0.95 THz, (d) f = 1.0 THz.
图 7 棋盘式1-bit太赫兹频率编码器 (a) f = 0.4 THz, (b) f = 0.75 THz, (c) f = 0.95 THz, (d) f = 1.0 THz时的二维电场图
Fig. 7. Chessboard 1-bit terahertz frequency coding metasurface: Two-dimensional electric field pattern of (a) f = 0.4 THz, (b) f = 0.75 THz, (c) f = 0.95 THz, (d) f = 1.0 THz.
图 6 棋盘式1-bit太赫兹频率编码器 (a) f = 0.4 THz, (b) f = 0.75 THz, (c) f = 0.95 THz, (d) f = 1.0 THz时的三维远场图
Fig. 6. Chessboard 1-bit terahertz frequency coding metasurface: Three-dimensional far-field pattern of (a) f = 0.4 THz, (b) f = 0.75 THz, (c) f = 0.95 THz, (d) f = 1.0 THz.
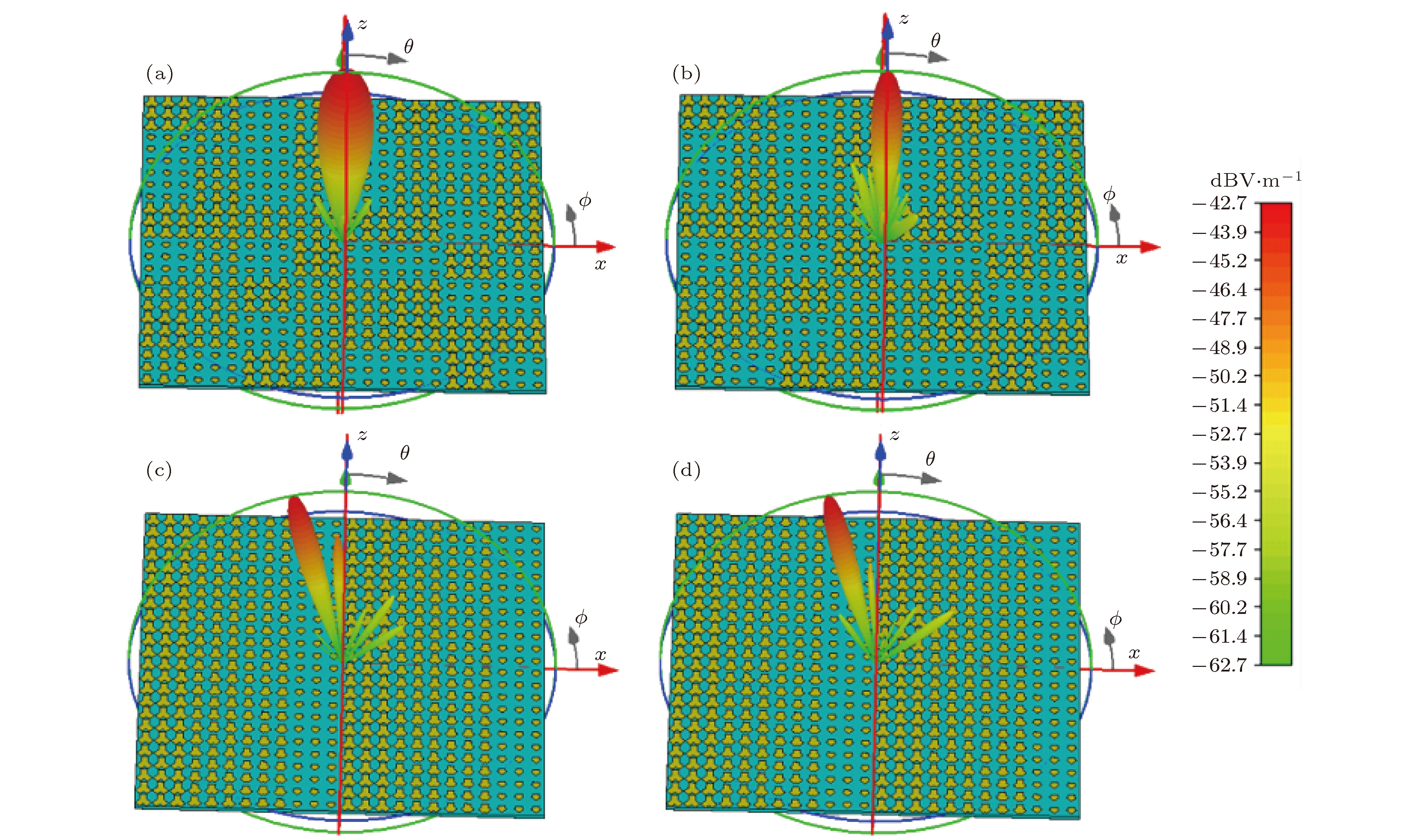
图 8 “00-00, 00-01, 00-10, 00-11”周期排布的2-bit太赫兹频率编码器 (a) f = 0.4 THz, (b) f = 0.75 THz, (c) f = 0.95 THz, (d) f = 1.0 THz时的三维远场图
Fig. 8. 2-bit periodic terahertz frequency coding metasurfacearranged along x direction with “00-00, 00-01, 00-10, 00-11” sequence: Three-dimensionalfar-field pattern of (a) f = 0.4 THz, (b) f = 0.75 THz, (c) f = 0.95 THz, (d) f = 1.0 THz.
图 11 2-bit太赫兹随机频率编码器 (a) f = 0.4 THz, (b) f = 0.75 THz, (c) f = 0.95 THz, (d) f = 1.0 THz时二维电场图
Fig. 11. 2-bit random terahertz frequency coding metasurface:two-dimensional electric field pattern of (a) f = 0.4 THz, (b) f = 0.75 THz, (c) f = 0.95 THz, (d) f = 1.0 THz.
图 10 2-bit太赫兹随机频率编码器 (a) f = 0.4 THz, (b) f = 0.75 THz, (c) f = 0.95 THz, (d) f = 1.0 THz时的三维远场图
Fig. 10. 2-bit random terahertz frequency coding metasurface: Three-dimensional far-field pattern of (a) f = 0.4 THz, (b) f = 0.75 THz, (c) f = 0.95 THz, (d) f = 1.0 THz.
图 9 “00-00, 00-01, 00-10, 00-11”周期排布的2-bit太赫兹频率编码器 (a) f = 0.4 THz, (b) f = 0.75 THz, (c) f = 0.95 THz, (d) f = 1.0 THz时的二维电场图
Fig. 9. 2-bit periodic terahertz frequency coding metasurface arranged along x direction with “00-00, 00-01, 00-10, 00-11” sequence: Two-dimensionalelectric field pattern of (a) f = 0.4 THz, (b) f = 0.75 THz, (c) f = 0.95 THz, (d) f = 1.0 THz.
图 12 2-bit太赫兹随机频率编码器和金属板在1.0 THz处的雷达散射截面分布
Fig. 12. Radar cross section distribution of 2-bit terahertz random frequency coding metasurface and metal plate at 1.0 THz.
图 13 2-bit非周期排布太赫兹频率编码器 (a) f = 0.4 THz, (b) f = 0.75 THz, (c) f = 0.95 THz, (d) f = 1.0 THz时的三维远场图
Fig. 13. Fig. 10. 2-bit non-periodic terahertz frequency coding metasurface: Three-dimensional far-field pattern of (a) f = 0.4 THz, (b) f = 0.75 THz, (c) f = 0.95 THz, (d) f = 1.0 THz.
图 14 2-bit非周期排布太赫兹频率编码器 (a) f = 0.4 THz, (b) f = 0.75 THz, (c) f = 0.95 THz, (d) f = 1.0 THz时的二维电场图
Fig. 14. Fig. 10. 2-bit non-periodic terahertz frequency coding metasurface: Two-dimensional electric field pattern of (a) f = 0.4 THz, (b) f = 0.75 THz, (c) f = 0.95 THz, (d) f = 1.0 THz.
表 1 1-bit频率编码器单元
Table 1. 1-bit frequency terahertz coding metasurface unit.
单元结构 α0/(°) 1-bit相位响应 近似α0/(°) 空域码 α1/(°)·THz–1 近似α1/(°)·THz–1 频域码 编码状态 154 160 “0” –312/0.6 0/0.6 “0” “0–0” 158 160 “0” –138/0.6 180/0.6 “1” “0–1” 
下载: 导出CSV
-
[1] Yu N F, Genevet P, Kats M A, Aieta F, Tetienne P J, Capasso F, Gaburro Z 2011 Science 334 333
Google Scholar
[2] Yu N F,Capasso F 2014 Nat. Mater. 13 139
Google Scholar
[3] Liu L X, Zhang X Q, Kenney M, Su X Q, Xu N N, Ouyang C M, Shi Y L, Han J G, Zhang W L, Zhang S 2014 Adv. Mater. 26 5031
Google Scholar
[4] Li Y F, Zhang J Q, Qu S B, Wang J F, Chen H Y, Xu Z, Zhang A X 2014 J. Appl. Phys. 115 063908
Google Scholar
[5] Yu Y F, Zhu A Y, Paniagua-Domínguez R, Fu Y H, Luk'Yanchuk B, Kuznetsov A I 2015 Laser Photon. Rev. 9 412
Google Scholar
[6] Li Y F, Zhang J Q, Qu S B, Wang J F, Zheng L, Pang Y Q, Xu Z, Zheng A X 2015 J. Appl. Phys. 117 044501
Google Scholar
[7] Zhu H F, Semperlotti F 2016 Phys. Rev. Lett. 117 034302
Google Scholar
[8] Wang L, Kruk S, Tang H Z, Li T, Kravchenko I, Neshev D N, Kivshar Y S 2016 Optica 3 1504
Google Scholar
[9] Li Y F, Zhang J Q, Qu S B, Wang J F, Chen H Y, Xu Z, Zhang A X 2014 Appl. Phys. Lett. 104 221110
Google Scholar
[10] Ramli M N, Ping J S, Jamlos M F, Lago H, Aziz N M, Al-Hadi A A 2017 Appl. Phys. A 123 149
Google Scholar
[11] Xu H X, Wang G M, Liang J G, Qi M Q, Gao X 2013 IEEE Trans. Antennas Propag. 61 3442
Google Scholar
[12] Wan X, Shen X P, Luo Y, Cui T J 2014 Laser Photon. Rev. 8 757
Google Scholar
[13] Li Z L, Kim I, Zhang L, Mehmood M Q, Anwar M S, Saleem M, Lee D, Nam K T, Zhang S, Luk'Yanchuk B, Wang Y, Zheng G X, Rho J, Qiu C W 2017A CS Nano 11 9382
Google Scholar
[14] Cui TJ, Liu S, Li L L 2016 Light Sci. Appl. 5 e16172
Google Scholar
[15] Huang C, Sun B, Pan W B, Cui J H, Wu X Y, Luo X G 2017 Sci. Rep. 7 42302
Google Scholar
[16] Li J S, Zhao Z J, Yao J Q 2017 Opt. Express 25 29983
Google Scholar
[17] Cui T J, Liu S 2017 Adv. Opt. Mater. 5 1700624
Google Scholar
[18] Li L L, Cui T J, Ji W, Liu S, Ding J, Wan X, Li Y B, Jiang M H, Qiu C W, Zhang S 2017 Nat. Commun. 8 197
Google Scholar
[19] Su J X, Cui Y Y, Li Z R, Yan Q L, Che Y X, Yin H C 2018 AIP Adv. 8 035027
Google Scholar
[20] Li J S, Yao J Q 2018 IEEE Photon. J. 10 1
Google Scholar
下载:
计量
- 文章访问数: 8653
- PDF下载量: 156
- 被引次数: 0
