-
目前学者们普遍认为, 平面相控阵的方向性系数在扫描过程中按照余弦规律变化, 无法实现从侧射到端射的大角度范围波束扫描. 为了明晰面阵扫描方向图的变化规律, 本文从阵因子的严格公式出发, 分析了不同规模平面相控阵的方向性系数随扫描角度的变化, 并将由严格阵因子公式得到的方向性系数变化趋势与余弦规律进行了比较. 分析表明, 有限大面阵的方向性系数在近端射区域不满足余弦变化规律, 且在端射区域不为零. 基于上述结论, 本文进一步提出了采用单元方向图赋形弥补阵因子方向性系数变化的思路, 为平面相控阵实现超大角度范围波束扫描指明了方向.At present, researchers generally believe that the change of maximum directivity of planar phased arrays in beam scanning process conforms with the cosine law, so that the wide-range beam scanning from broadside to end-fire is impossible to realize. There are three main factors that affect the scanning range of the planar phased array antenna: 1) array factor; 2) element pattern; 3) port impedance matching. Scholars have done a lot of researches on the element pattern and the port impedance matching. About the array factor, Elliott, a famous phased array scholar, made a theoretical study on the directivity of the linear array and the planar array in 1963 and 1964, concluding that the variation of directivity of planar phased array conforms with the cosine law. However, the above conclusion came from an approximate formula under certain conditions: 1) the element pattern in the half-space is omnidirectional; 2) the beam of a large array is narrow enough; 3) the beam cannot scan a range of several beamwidths close to end-fire. To make clear the scanning beam’s change law of planar arrays, the law of directivity changing with scanning angle of linear array and planar phased array with different sizes are analyzed by using the strict formula of array factor, and the directivity’s change law derived from strict formula of array factor is compared with the cosine law. The results show that 1) the variation law of the directivity of a linear array depends on the spacing between elements. When the spacing between elements is equal to half a wavelength, the directivity of the array does not change with the scanning angle. When the spacing between elements is less than half a wavelength, the directivity of the array increases with scanning angle increasing. 2) The directivity of a finite array decreases with scanning angle increasing. However, the scanning beam’s maximum directivity of a finite planar phased array does not satisfy the cosine law and it is not zero in the end-fire range. Based on the above conclusions, the idea that the change of array factor’s directivity is compensated for by element beamforming is further proposed, which points out a direction for realizing the ultra-wide-angle-range beam scanning of planar phased arrays.
-
Keywords:
- planar array antenna /
- wide-angle scanning /
- array factor /
- element beamforming
[1] Kmetzo J 1967 IEEE Trans. Antennas Propag. 15 367
Google Scholar
[2] Valavan S E, Tran D, Yarovoy A G, Roederer A G 2014 IEEE Trans. Antennas Propag. 62 5370
Google Scholar
[3] Toshev A G 2008 IEEE Trans. Antennas Propag. 56 3330
Google Scholar
[4] Bai Y Y, Xiao S Q, Tang M C, Ding Z F, Wang B Z 2011 IEEE Trans. Antennas Propag. 59 4071
Google Scholar
[5] 杨浩楠, 曹祥玉, 高军, 杨欢欢, 李桐 2021 70 014101
Google Scholar
Yang H N, Cao X Y, Gao J, Yang H H, Li T 2021 Acta Phys. Sin. 70 014101
Google Scholar
[6] 郑月军, 高军, 曹祥玉, 郑秋容, 李思佳, 李文强, 杨群 2014 63 224102
Google Scholar
Zheng Y J, Gao J, Cao X Y, Zheng Q R, Li S J, Li W Q, Yang Q 2014 Acta Phys. Sin 63 224102
Google Scholar
[7] Zhang Y, Liu H, Meng C 2020 Prog. Electromagn. Res. 168 31
Google Scholar
[8] Ouedraogo S, Hinostroza Saenz I D, Guinvarc'h R 2019 Prog. Electromagn. Res. 164 17
Google Scholar
[9] Ding X, Wang B Z, He G Q 2013 IEEE Trans. Antennas Propag. 61 5319
Google Scholar
[10] Cheng Y F, Ding X, Shao W, Wang B Z 2017 IEEE Trans. Antennas Propag. 65 932
Google Scholar
[11] Wang R, Wang B Z, Ding X, Yang X S 2015 IEEE Trans. Antennas Propag. 63 3908
Google Scholar
[12] Wang R, Wang B Z, Hu C H, Gong C, Ding X 2016 Prog. Electromag. Res. 156 13
Google Scholar
[13] Wen Y, Wang B Z, Ding X 2016 IEEE Trans. Antennas Propag. 64 805
Google Scholar
[14] Wang R, Wang B Z, Hu C H, Ding X 2017 Sci. Rep. 7 2729
Google Scholar
[15] Xia R L, Qu S W, Li P F, Yang D Q, Yang S W, Nie Z P 2015 IEEE Trans. Antennas. Propag. 63 5161
Google Scholar
[16] Abbasi Arand B, Bazrkar A, Zahedi A 2017 IEEE Trans. Antennas. Propag. 65 2983
Google Scholar
[17] Oliveri G, Viani F, Anselmi N, Massa A 2015 IEEE Trans. Antennas. Propag. 63 2482
Google Scholar
[18] Hu C H, Wang B Z, Wang R, Xiao S Q, Ding X 2020 IEEE Trans. Antennas. Propag. 68 2788
Google Scholar
[19] Yetisir E, Ghalichechian N, Volakis J L 2016 IEEE Trans. Antennas. Propag. 64 4256
Google Scholar
[20] Elliott R S 1963 Beamwidth and Directivity of Large Scanning Arrays: Part I [J] Microwave J. Vol. 6 pp53–60
[21] Elliott R S 1964 Beamwidth and Directivity of Large Scanning Arrays: Part II [J] Microwave J. Vol. 7 pp74–82
[22] Jiang Z, Xiao S, Yao Z, Wang B Z 2020 IEEE Trans. Antennas. Propag. 68 7348
Google Scholar
[23] -
图 2 一维阵因子在不同阵元间距扫描时的归一化方向性系数随扫描角度的变化 (a) 一维阵列尺寸为8λ; (b) 一维阵列尺寸为16λ; (c) 一维阵列尺寸为32λ; (d) 一维阵列尺寸为64λ
Fig. 2. Normalized directivity of the linear array factor varies with different element spaces and different scanning angles: (a) The size of the linear array factor is 8λ; (b) the size of the linear array factor is 16λ; (c) the size of the linear array factor is 32λ; (d) the size of the linear array factor is 64λ.
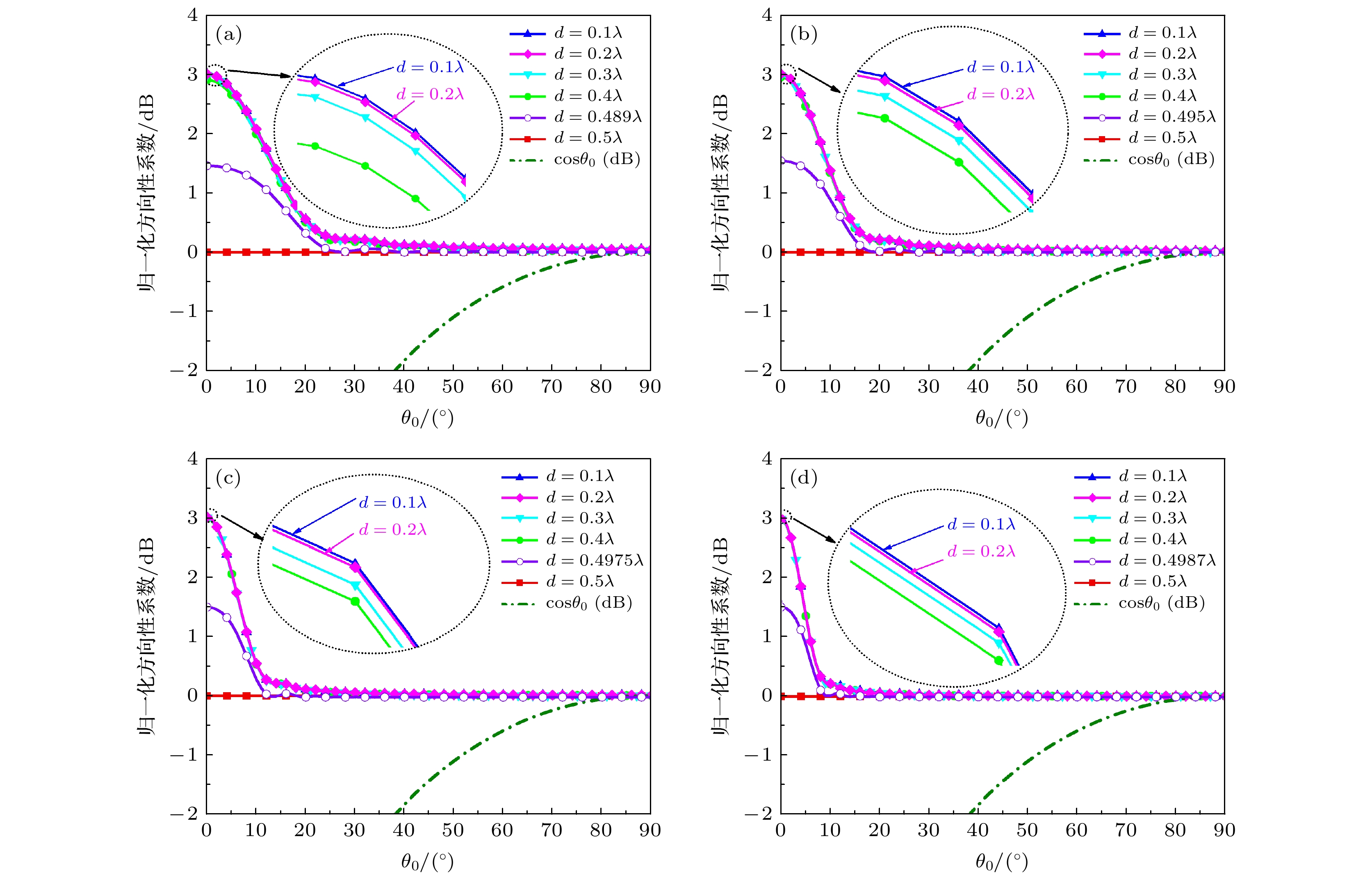
图 4 平面阵阵因子归一化最大方向性系数随扫描角度的变化情况(φ = 0°) (a) 8λ × 8λ阵列; (b) 16λ × 16λ阵列; (c) 32λ × 32λ阵列; (d) 64λ × 64λ阵列; (e) 128λ × 128λ阵列; (f) 256λ × 256λ阵列
Fig. 4. Normalized directivity of the planar array factor varies with different element spaces and different scanning angles (φ = 0°): (a) The size of the planar array factor is 8λ × 8λ; (b) the size of the planar array factor is 16λ × 16λ; (c) the size of the planar array factor is 32λ × 32λ; (d) the size of the planar array factor is 64λ × 64λ; (e) the size of the planar array factor is 128λ × 128λ; (f) the size of the planar array factor is 256λ × 256λ.
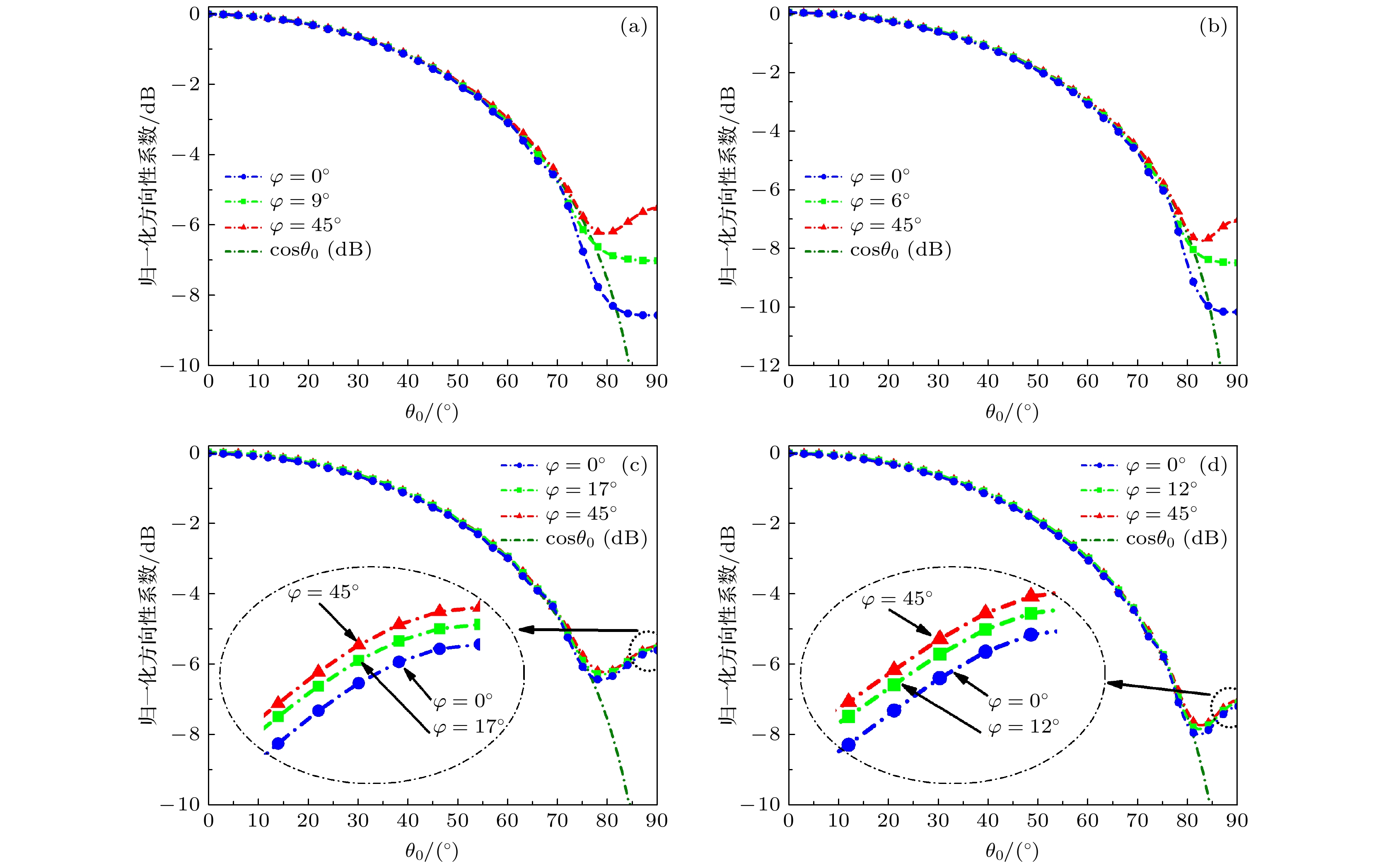
图 5 平面阵阵因子归一化最大方向性系数在不同单元间距和不同φ值时随扫描角度的变化情况 (a) 16λ × 16λ阵列(d = 0.5λ); (b) 32λ × 32λ阵列(d = 0.5λ); (c) 16λ × 16λ阵列(d = 0.4λ); (d) 32λ × 32λ阵列(d = 0.4λ)
Fig. 5. Normalized directivity of the planar array factor varies with different element spaces, different scanning angles, and different φ: (a) The size of the planar array factor is 16λ × 16λ (d = 0.5λ); (b) the size of the planar array factor is 32λ × 32λ (d = 0.5λ); (c) the size of the planar array factor is 16λ × 16λ (d = 0.4λ); (d) the size of the planar array factor is 32λ × 32λ (d = 0.4λ).
-
[1] Kmetzo J 1967 IEEE Trans. Antennas Propag. 15 367
Google Scholar
[2] Valavan S E, Tran D, Yarovoy A G, Roederer A G 2014 IEEE Trans. Antennas Propag. 62 5370
Google Scholar
[3] Toshev A G 2008 IEEE Trans. Antennas Propag. 56 3330
Google Scholar
[4] Bai Y Y, Xiao S Q, Tang M C, Ding Z F, Wang B Z 2011 IEEE Trans. Antennas Propag. 59 4071
Google Scholar
[5] 杨浩楠, 曹祥玉, 高军, 杨欢欢, 李桐 2021 70 014101
Google Scholar
Yang H N, Cao X Y, Gao J, Yang H H, Li T 2021 Acta Phys. Sin. 70 014101
Google Scholar
[6] 郑月军, 高军, 曹祥玉, 郑秋容, 李思佳, 李文强, 杨群 2014 63 224102
Google Scholar
Zheng Y J, Gao J, Cao X Y, Zheng Q R, Li S J, Li W Q, Yang Q 2014 Acta Phys. Sin 63 224102
Google Scholar
[7] Zhang Y, Liu H, Meng C 2020 Prog. Electromagn. Res. 168 31
Google Scholar
[8] Ouedraogo S, Hinostroza Saenz I D, Guinvarc'h R 2019 Prog. Electromagn. Res. 164 17
Google Scholar
[9] Ding X, Wang B Z, He G Q 2013 IEEE Trans. Antennas Propag. 61 5319
Google Scholar
[10] Cheng Y F, Ding X, Shao W, Wang B Z 2017 IEEE Trans. Antennas Propag. 65 932
Google Scholar
[11] Wang R, Wang B Z, Ding X, Yang X S 2015 IEEE Trans. Antennas Propag. 63 3908
Google Scholar
[12] Wang R, Wang B Z, Hu C H, Gong C, Ding X 2016 Prog. Electromag. Res. 156 13
Google Scholar
[13] Wen Y, Wang B Z, Ding X 2016 IEEE Trans. Antennas Propag. 64 805
Google Scholar
[14] Wang R, Wang B Z, Hu C H, Ding X 2017 Sci. Rep. 7 2729
Google Scholar
[15] Xia R L, Qu S W, Li P F, Yang D Q, Yang S W, Nie Z P 2015 IEEE Trans. Antennas. Propag. 63 5161
Google Scholar
[16] Abbasi Arand B, Bazrkar A, Zahedi A 2017 IEEE Trans. Antennas. Propag. 65 2983
Google Scholar
[17] Oliveri G, Viani F, Anselmi N, Massa A 2015 IEEE Trans. Antennas. Propag. 63 2482
Google Scholar
[18] Hu C H, Wang B Z, Wang R, Xiao S Q, Ding X 2020 IEEE Trans. Antennas. Propag. 68 2788
Google Scholar
[19] Yetisir E, Ghalichechian N, Volakis J L 2016 IEEE Trans. Antennas. Propag. 64 4256
Google Scholar
[20] Elliott R S 1963 Beamwidth and Directivity of Large Scanning Arrays: Part I [J] Microwave J. Vol. 6 pp53–60
[21] Elliott R S 1964 Beamwidth and Directivity of Large Scanning Arrays: Part II [J] Microwave J. Vol. 7 pp74–82
[22] Jiang Z, Xiao S, Yao Z, Wang B Z 2020 IEEE Trans. Antennas. Propag. 68 7348
Google Scholar
[23]
下载:
计量
- 文章访问数: 8661
- PDF下载量: 228
- 被引次数: 0
