腔自旋波混合系统的研究进展

沈瑞昌; 张国强; 王逸璞; 游建强

doi:10.7498/aps.68.20191608

摘要

近年来腔自旋波混合系统引起人们的研究兴趣. 基于自旋波体系的优点, 有望建立一个以自旋波量子为核心的、实现不同物理系统之间信息传递的平台. 本文简要介绍了腔自旋波混合系统的发展进程, 阐明自旋波量子与微波腔光子的耦合机制; 着重介绍了近期在腔自旋波混合系统中关于非线性和赝厄米性方面的研究进展, 其中包括非线性效应引起的腔自旋波量子极化激元的双稳, 宇称-时间(PT)对称哈密顿量的实现和PT对称自发破缺相变二阶奇点的观测, 以及如何构造非PT对称的赝厄米哈密顿量来实现三阶奇点等.

关键词:

Abstract

Recently, the hybrid cavity-magnon system has attracted considerable interest. Owing to the good tunability of magnons, it is promising to use the magnons as a core to implement a hybrid quantum platform for transferring information among different quantum systems. In this article, we first briefly review the cavity magnonic systems and clarify the coupling mechanism between magnons and microwave photons. Then, we introduce the latest research progress in the aspects of nonlinearity and pseudo-Hermiticity, including the bistability of cavity magnon polaritons, observation of the second-order exceptional point in a PT-symmetric hybrid cavity-magnon system, and the pseudo-Hermiticity with a third-order exceptional point.

Keywords:

hybrid cavity-magnon system /
cavity magon polariton /
Kerr effect and bistability /
pseudo-Hermiticity and exceptional point

作者及机构信息

1.
北京计算科学研究中心, 量子物理与量子信息部, 北京　100193

2.
浙江大学物理系, 杭州　310027

通信作者: 游建强, jqyou@zju.edu.cn

作者简介:

游建强, 浙江大学物理系求是特聘教授、博士生导师. 研究领域为量子计算与量子信息、量子光学和凝聚态物理. 1984年7月在湘潭大学物理系获物理学专业学士学位, 1988年8月在中国科学院金属研究所获金属物理专业硕士学位, 1997年7月在中国科学院固体物理研究所获凝聚态物理专业博士学位. 曾任北京计算科学研究中心讲座教授、复旦大学物理系谢希德冠名教授等. 2006年获国家杰出青年科学基金, 2008年入选教育部长江学者特聘教授. 2016年承担科技部国家重点研发计划重点专项项目, 任项目首席. 1999年获安徽省自然科学奖二等奖, 2003年获日本理化学研究所前沿研究头等奖 (RIKEN Frontier Research System Grand Award). 现为德国Springer出版社Quantum Information Processing杂志和美国物理学会Physical Review Applied杂志编委

基金项目: 国家重点基础研究发展计划(批准号: 2016 YFA0301200)和国家自然科学基金(批准号: 11934010, U1801661, U1930402)资助的课题

Authors and contacts

1.
Quantum Physics and Quantum Information Division, Beijing Computational Science Research Center, Beijing 100193, China

2.
Department of Physics, Zhejiang University, Hangzhou 310027, China

Corresponding author: You Jian-Qiang, jqyou@zju.edu.cn

Funds: Project supported by the State Key Development Program for Basic Research of China (Grant No. 2016 YFA0301200) and the National Natural Science Foundation of China (Grant Nos. 11934010, U1801661, U1930402)

文章全文 : translate this paragraph

参考文献

[1]	Shor P W 1994 Proceedings of 35 th Annual Symposium on Foundations of Computer Scienece Los Alamitos, USA, November 22–24, 1994 p124
[2]	Grover L K 1996 Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing New York, USA, May 22–24, 1996 p212
[3]	Buluta I, Ashhab S, Nori F 2011 Rep. Prog. Phys. 74 104401 Google Scholar
[4]	Blatt R, Roos C F 2012 Nat. Phys. 8 277 Google Scholar
[5]	Hanson R, Kouwenhoven L P, Petta J R, Tarucha S, Vandersypen L M K 2007 Rev. Mod. Phys. 79 1217 Google Scholar
[6]	孔祥宇, 朱垣晔, 闻经纬, 新涛, 李可仁, 龙桂鲁 2018 67 220301 Google Scholar Kong X Y, Zhu Y Y, Wen J W, Xin T, Li K R, Long G L 2018 Acta Phys. Sin. 67 220301 Google Scholar
[7]	You J Q, Nori F 2005 Phys. Today 58 42
[8]	Devoret M H, Schoelkopf R J 2013 Science 339 1169 Google Scholar
[9]	You J Q, Hu X D, Ashhab S, Nori F 2007 Phys. Rev. B 75 140515 Google Scholar
[10]	Koch J, Yu T M, Gambetta J, Houck A A, Schuster D I, Majer J, Blais A, Devoret M H, Girvin S M, Schoelkopf R J 2007 Phys. Rev. A 76 042319 Google Scholar
[11]	Barends R, Kelly J, Megrant A, Veitia A, Sank D, Jeffrey E, White T C, Mutus J, Fowler A G, Campbell B, Chen Y, Chen Z, Chiaro B, Dunsworth A, Neill C, O’Malley P, Roushan P, Vainsencher A, Wenner J, Korotkov A N, Cleland A N, Martinis J M 2014 Nature 508 500 Google Scholar
[12]	Feynman R P 1986 Found. Phys. 16 507 Google Scholar
[13]	Nielsen M A, Chuang I L 2001 Quantum Computation and Quantum Information (London: Cambridge University Press) p702
[14]	Ladd T D, Jelezko F, Laflamme R, Nakamura Y, Monroe C, O’Brien J L 2010 Nature 464 45 Google Scholar
[15]	Feynman R P 1982 Int. J. Theor. Phys. 21 467 Google Scholar
[16]	Aspuru-Guzik A, Dutoi A D, Love P J, Head-Gordon M 2005 Science 309 1704 Google Scholar
[17]	Cirac J I, Zoller P 2012 Nat. Phys. 8 264 Google Scholar
[18]	Xiang Z L, Ashhab S, You J Q, Nori F 2013 Rev. Mod. Phys. 85 623 Google Scholar
[19]	Kurizkia G, Bertetb P, Kubob Y, Molmer K, Petrosyan D, Rabl P, Schmiedmayer J 2015 Proc. Natl. Acad. Sci. USA 112 3866 Google Scholar
[20]	Bienfait A, Pla J J, Kubo Y, Stern M, Zhou X, Lo C C, Weis C D, Schenkel T, Thewalt M L W, Vion D, Esteve D, Julsgaard B, Moelmer K, Morton J J L, Bertet P 2016 Nat. Nano 11 253
[21]	Raizen M G, Thompson R J, Brecha R J, Kimble H J, Carmichael H J 1989 Phys. Rev. Lett. 63 240 Google Scholar
[22]	Soykal Ö O, Flatté M E 2010 Phys. Rev. Lett. 104 077202
[23]	Soykal Ö O, Flatté M E 2010 Phys. Rev. B 82 104413 Google Scholar
[24]	Huebl H, Zollitsch C W, Lotze J, Hocke F, Greifenstein M, Marx A, Gross R, Goennenwein S T B 2013 Phys. Rev. Lett. 111 127003 Google Scholar
[25]	Zhang X, Zou C L, Jiang L, Tang H X 2014 Phys. Rev. Lett. 113 156401 Google Scholar
[26]	Tabuchi Y, Ishino S, Ishikawa T, Yamazaki R, Usami K, Nakamura Y 2014 Phys. Rev. Lett. 113 083603 Google Scholar
[27]	Zhang D K, Wang X M, Li T F, Luo X Q, Wu W D, Nori F, You J Q 2015 NPJ Quantum Inf. 1 15014 Google Scholar
[28]	Bai L H, Harder M, Chen Y P, Fan X, Xiao J Q, Hu C M 2015 Phys. Rev. Lett. 114 227201 Google Scholar
[29]	Haigh J A, Langenfeld S, Lambert N J, Baumberg J J, Ramsay A J, Nunnenkamp A, Ferguson A J 2015 Phys. Rev. A 92 063845 Google Scholar
[30]	Tabuchi Y, Ishino S, Noguchi A, Ishikawa T, Yamazaki R, Usami K, Nakamura Y 2015 Science 349 405 Google Scholar
[31]	Quirion D L, Tabuchi Y, Ishino S, Noguchi A, Ishikawa T, Yamazaki R, Nakamura Y 2017 Sci. Adv. 3 e1603150 Google Scholar
[32]	Zhang X F, Zou C L, Jiang L, Tang H X 2016 Sci. Adv. 2 e1501286 Google Scholar
[33]	Harder M, Yang Y, Yao B M, Yu C H, Rao J W, Gui Y S, Stamps R L, Hu C M 2018 Phys. Rev. Lett. 121 137203
[34]	Grigoryan V L, Shen K, Xia K 2018 Phys. Rev. B 98 024406 Google Scholar
[35]	Xu P C, Rao J W, Gui Y S, Jin X, Hu C M 2019 Phys. Rev. B 100 094415 Google Scholar
[36]	Yu W C, Wang J J, Yuan H Y, Xiao J 2019 arXiv: 1907.06222 v2 [cond-mat. mes-hall]
[37]	Yuan H Y, Peng Y P, Zheng S S, He Q Y, Xia K, Yung M H 2019 arXiv: 1905.11117 v1 [cond-mat. mes-hall]
[38]	Wang Y P, Rao J W, Yang Y, Xu P C, Gui Y S, Yao B M, You J Q, Hu C M 2019 Phys. Rev. Lett. 123 127202 Google Scholar
[39]	Quirion D L, Tabuchi Y, Gloppe A, Usami K, Nakamura Y 2019 Appl. Phys. Express 12 070101 Google Scholar
[40]	Wang Y P, Zhang G Q, Zhang D K, Luo X Q, Xiong W, Wang S P, Li T F, Hu C M, You J Q 2016 Phys. Rev. B 94 224410 Google Scholar
[41]	Wang Y P, Zhang G Q, Zhang D K, Li T F, Hu C M, You J Q 2018 Phys. Rev. Lett. 120 057202 Google Scholar
[42]	Zhang D K, Luo X Q, Wang Y P, Li T F, You J Q 2017 Nat. Com. 8 1368 Google Scholar
[43]	Zhang G Q, You J Q 2019 Phys. Rev. B 99 054404 Google Scholar
[44]	Holstein T, Primakoff H 1940 Phys. Rev. 58 1098 Google Scholar
[45]	Kostylev N, Goryachev M, Tobar M E 2016 Appl. Phys. Lett. 108 062402 Google Scholar
[46]	Rezende S M, de Aguiar F M 1990 Proc. IEEE 78 893 Google Scholar
[47]	Zhang G Q, Wang Y P, You J Q 2019 Sci. China: Phys. Mech. Astron. 62 987511 Google Scholar
[48]	Bogoliubov N N 1958 Phys. Today 34 1
[49]	Harder M, Bai L H, Match C, Sirker J, Hu C M 2016 Sci. China: Phys. Mech. Astron. 59 117511 Google Scholar
[50]	Bender C M, Boettcher S 1998 Phys. Rev. Lett. 80 5243 Google Scholar
[51]	Konotop V V, Yang J, Zezyulin D A 2016 Rev. Mod. Phys. 88 035002 Google Scholar
[52]	Mostafazadeh A 2002 J. Math. Phys. 43 205 Google Scholar
[53]	Mostafazadeh A 2002 J. Math. Phys. 43 2814 Google Scholar
[54]	Grigoryan V L, Xia K 2019 Phys. Rev. B 99 224408 Google Scholar
[55]	Cao Y S, Yan P 2019 Phys. Rev. B 99 214415 Google Scholar

施引文献

图 1 YIG小球和三维微波腔耦合系统示意图及腔内磁场分布模拟图^[41]

Fig. 1. Schematic of YIG sphere and three-dimensional microwave cavity coupling system and the simulation of magnetic field distribution in cavity^[41].

下载: 全尺寸图片幻灯片

图 2 自旋波模和腔模共振时下支极化激元的频率移动随驱动功率变化情况　(a)偏置磁场沿晶轴[100]的情况; (b)偏置磁场沿晶轴[110]的情况^[41]

Fig. 2. When the magnon resonated with the cavity mode, the curves of the frequency shift of the lower-branch cavity magnon polaritons ${\varDelta _{{\rm{LP}}}}$ versus the driving power${P_{\rm{d}}}$: (a) The bias magnetic field is along the crystal axis [100]; (b) the bias magnetic field is along the crystal axis [110]^[41].

下载: 全尺寸图片幻灯片

图 3 赝厄米哈密顿量、PT对称哈密顿量和厄米哈密顿量之间关系示意图

Fig. 3. Relationship between the pseudo-Hermitian, the PT-symmetric Hamiltonian and the Hermitian Hamiltonian.

下载: 全尺寸图片幻灯片

图 4 PT对称系统示意图　(a)实验装置示意图; (b)腔TE₁₀₁模和TE₁₀₂模磁场分布模拟图^[42]

Fig. 4. Schematic of PT-symmetrical system: (a) The schematic of experimental device; (b) the simulation of cavity mode ${\rm{T}}{{\rm{E}}_{101}}$ and ${\rm{T}}{{\rm{E}}_{102}}$^[42].

下载: 全尺寸图片幻灯片

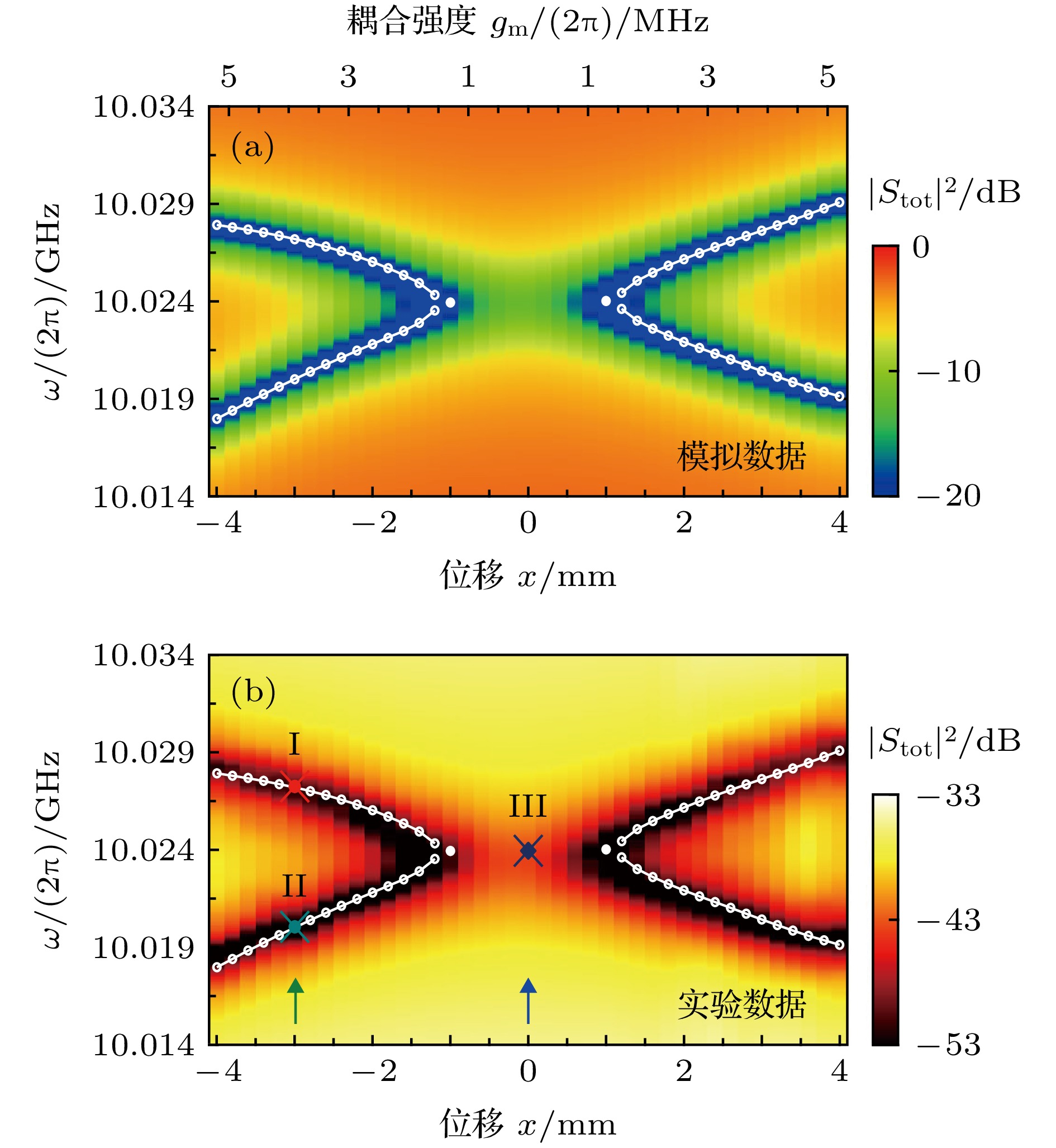
图 5 PT对称系统中总传输谱${\left| {{S_{{\rm{tot}}}}\left( \omega \right)} \right|^2}$随YIG小球位置x以及输入场频率$\omega $的变化情况　(a)理论模拟结果; (b)实验结果^[42]

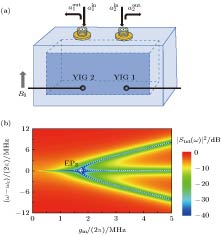
Fig. 5. The total transmission spectrum ${\left| {{S_{{\rm{tot}}}}\left( \omega \right)} \right|^2}$ versus the position of YIG sphere $x$ and the frequency of input field $\omega $: (a) The theoretical simulation results; (b) the experimental results^[42].

下载: 全尺寸图片幻灯片

图 6 赝厄米系统示意图和理论结果模拟图^[47]　(a)赝厄米系统示意图; (b)理论模拟总传输谱${\left| {{S_{{\rm{tot}}}}\left( \omega \right)} \right|^2}$随耦合强度${g_1}$以及输入场和腔模之间的频率失谐量$\omega - {\omega _{\rm{c}}}$的变化情况

Fig. 6. The system schematic and the simulation of theoretical results of pseudo-Hermitian system^[47]: (a) The schematic of pseudo-Hermitian system; (b) the total transmission spectrum ${\left| {{S_{{\rm{tot}}}}\left( \omega \right)} \right|^2}$ versus the coupling strength ${g_1}$ and the frequency detuning between the input field and the cavity mode $\omega - {\omega _{\rm{c}}}$.

下载: 全尺寸图片幻灯片

map

[1]	Shor P W 1994 Proceedings of 35 th Annual Symposium on Foundations of Computer Scienece Los Alamitos, USA, November 22–24, 1994 p124
[2]	Grover L K 1996 Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing New York, USA, May 22–24, 1996 p212
[3]	Buluta I, Ashhab S, Nori F 2011 Rep. Prog. Phys. 74 104401 Google Scholar
[4]	Blatt R, Roos C F 2012 Nat. Phys. 8 277 Google Scholar
[5]	Hanson R, Kouwenhoven L P, Petta J R, Tarucha S, Vandersypen L M K 2007 Rev. Mod. Phys. 79 1217 Google Scholar
[6]	孔祥宇, 朱垣晔, 闻经纬, 新涛, 李可仁, 龙桂鲁 2018 67 220301 Google Scholar Kong X Y, Zhu Y Y, Wen J W, Xin T, Li K R, Long G L 2018 Acta Phys. Sin. 67 220301 Google Scholar
[7]	You J Q, Nori F 2005 Phys. Today 58 42
[8]	Devoret M H, Schoelkopf R J 2013 Science 339 1169 Google Scholar
[9]	You J Q, Hu X D, Ashhab S, Nori F 2007 Phys. Rev. B 75 140515 Google Scholar
[10]	Koch J, Yu T M, Gambetta J, Houck A A, Schuster D I, Majer J, Blais A, Devoret M H, Girvin S M, Schoelkopf R J 2007 Phys. Rev. A 76 042319 Google Scholar
[11]	Barends R, Kelly J, Megrant A, Veitia A, Sank D, Jeffrey E, White T C, Mutus J, Fowler A G, Campbell B, Chen Y, Chen Z, Chiaro B, Dunsworth A, Neill C, O’Malley P, Roushan P, Vainsencher A, Wenner J, Korotkov A N, Cleland A N, Martinis J M 2014 Nature 508 500 Google Scholar
[12]	Feynman R P 1986 Found. Phys. 16 507 Google Scholar
[13]	Nielsen M A, Chuang I L 2001 Quantum Computation and Quantum Information (London: Cambridge University Press) p702
[14]	Ladd T D, Jelezko F, Laflamme R, Nakamura Y, Monroe C, O’Brien J L 2010 Nature 464 45 Google Scholar
[15]	Feynman R P 1982 Int. J. Theor. Phys. 21 467 Google Scholar
[16]	Aspuru-Guzik A, Dutoi A D, Love P J, Head-Gordon M 2005 Science 309 1704 Google Scholar
[17]	Cirac J I, Zoller P 2012 Nat. Phys. 8 264 Google Scholar
[18]	Xiang Z L, Ashhab S, You J Q, Nori F 2013 Rev. Mod. Phys. 85 623 Google Scholar
[19]	Kurizkia G, Bertetb P, Kubob Y, Molmer K, Petrosyan D, Rabl P, Schmiedmayer J 2015 Proc. Natl. Acad. Sci. USA 112 3866 Google Scholar
[20]	Bienfait A, Pla J J, Kubo Y, Stern M, Zhou X, Lo C C, Weis C D, Schenkel T, Thewalt M L W, Vion D, Esteve D, Julsgaard B, Moelmer K, Morton J J L, Bertet P 2016 Nat. Nano 11 253
[21]	Raizen M G, Thompson R J, Brecha R J, Kimble H J, Carmichael H J 1989 Phys. Rev. Lett. 63 240 Google Scholar
[22]	Soykal Ö O, Flatté M E 2010 Phys. Rev. Lett. 104 077202
[23]	Soykal Ö O, Flatté M E 2010 Phys. Rev. B 82 104413 Google Scholar
[24]	Huebl H, Zollitsch C W, Lotze J, Hocke F, Greifenstein M, Marx A, Gross R, Goennenwein S T B 2013 Phys. Rev. Lett. 111 127003 Google Scholar
[25]	Zhang X, Zou C L, Jiang L, Tang H X 2014 Phys. Rev. Lett. 113 156401 Google Scholar
[26]	Tabuchi Y, Ishino S, Ishikawa T, Yamazaki R, Usami K, Nakamura Y 2014 Phys. Rev. Lett. 113 083603 Google Scholar
[27]	Zhang D K, Wang X M, Li T F, Luo X Q, Wu W D, Nori F, You J Q 2015 NPJ Quantum Inf. 1 15014 Google Scholar
[28]	Bai L H, Harder M, Chen Y P, Fan X, Xiao J Q, Hu C M 2015 Phys. Rev. Lett. 114 227201 Google Scholar
[29]	Haigh J A, Langenfeld S, Lambert N J, Baumberg J J, Ramsay A J, Nunnenkamp A, Ferguson A J 2015 Phys. Rev. A 92 063845 Google Scholar
[30]	Tabuchi Y, Ishino S, Noguchi A, Ishikawa T, Yamazaki R, Usami K, Nakamura Y 2015 Science 349 405 Google Scholar
[31]	Quirion D L, Tabuchi Y, Ishino S, Noguchi A, Ishikawa T, Yamazaki R, Nakamura Y 2017 Sci. Adv. 3 e1603150 Google Scholar
[32]	Zhang X F, Zou C L, Jiang L, Tang H X 2016 Sci. Adv. 2 e1501286 Google Scholar
[33]	Harder M, Yang Y, Yao B M, Yu C H, Rao J W, Gui Y S, Stamps R L, Hu C M 2018 Phys. Rev. Lett. 121 137203
[34]	Grigoryan V L, Shen K, Xia K 2018 Phys. Rev. B 98 024406 Google Scholar
[35]	Xu P C, Rao J W, Gui Y S, Jin X, Hu C M 2019 Phys. Rev. B 100 094415 Google Scholar
[36]	Yu W C, Wang J J, Yuan H Y, Xiao J 2019 arXiv: 1907.06222 v2 [cond-mat. mes-hall]
[37]	Yuan H Y, Peng Y P, Zheng S S, He Q Y, Xia K, Yung M H 2019 arXiv: 1905.11117 v1 [cond-mat. mes-hall]
[38]	Wang Y P, Rao J W, Yang Y, Xu P C, Gui Y S, Yao B M, You J Q, Hu C M 2019 Phys. Rev. Lett. 123 127202 Google Scholar
[39]	Quirion D L, Tabuchi Y, Gloppe A, Usami K, Nakamura Y 2019 Appl. Phys. Express 12 070101 Google Scholar
[40]	Wang Y P, Zhang G Q, Zhang D K, Luo X Q, Xiong W, Wang S P, Li T F, Hu C M, You J Q 2016 Phys. Rev. B 94 224410 Google Scholar
[41]	Wang Y P, Zhang G Q, Zhang D K, Li T F, Hu C M, You J Q 2018 Phys. Rev. Lett. 120 057202 Google Scholar
[42]	Zhang D K, Luo X Q, Wang Y P, Li T F, You J Q 2017 Nat. Com. 8 1368 Google Scholar
[43]	Zhang G Q, You J Q 2019 Phys. Rev. B 99 054404 Google Scholar
[44]	Holstein T, Primakoff H 1940 Phys. Rev. 58 1098 Google Scholar
[45]	Kostylev N, Goryachev M, Tobar M E 2016 Appl. Phys. Lett. 108 062402 Google Scholar
[46]	Rezende S M, de Aguiar F M 1990 Proc. IEEE 78 893 Google Scholar
[47]	Zhang G Q, Wang Y P, You J Q 2019 Sci. China: Phys. Mech. Astron. 62 987511 Google Scholar
[48]	Bogoliubov N N 1958 Phys. Today 34 1
[49]	Harder M, Bai L H, Match C, Sirker J, Hu C M 2016 Sci. China: Phys. Mech. Astron. 59 117511 Google Scholar
[50]	Bender C M, Boettcher S 1998 Phys. Rev. Lett. 80 5243 Google Scholar
[51]	Konotop V V, Yang J, Zezyulin D A 2016 Rev. Mod. Phys. 88 035002 Google Scholar
[52]	Mostafazadeh A 2002 J. Math. Phys. 43 205 Google Scholar
[53]	Mostafazadeh A 2002 J. Math. Phys. 43 2814 Google Scholar
[54]	Grigoryan V L, Xia K 2019 Phys. Rev. B 99 224408 Google Scholar
[55]	Cao Y S, Yan P 2019 Phys. Rev. B 99 214415 Google Scholar

[1]	侯磊, 关舒阳, 尹俊, 张语军, 肖宜明, 徐文, 丁岚. 谐振腔-单层二硫化钼系统中的高阶腔耦合等离极化激元. , 2024, 73(22): 227102. doi: 10.7498/aps.73.20241106
[2]	李竞, 丁海涛, 张丹伟. 非厄米哈密顿量中的量子Fisher信息与参数估计. , 2023, 72(20): 200601. doi: 10.7498/aps.72.20230862
[3]	李家锐, 王梓安, 徐彤彤, 张莲莲, 公卫江. 一维${\cal {PT}}$对称非厄米自旋轨道耦合Su-Schrieffer-Heeger模型的拓扑性质. , 2022, 71(17): 177302. doi: 10.7498/aps.71.20220796
[4]	张禧征, 王鹏, 张坤亮, 杨学敏, 宋智. 非厄米临界动力学及其在量子多体系统中的应用. , 2022, 71(17): 174501. doi: 10.7498/aps.71.20220914
[5]	高雪儿, 李代莉, 刘志航, 郑超. 非厄米系统的量子模拟新进展. , 2022, 71(24): 240303. doi: 10.7498/aps.71.20221825
[6]	邓天舒. 畴壁系统中的非厄米趋肤效应. , 2022, 71(17): 170306. doi: 10.7498/aps.71.20221087
[7]	祝可嘉, 郭志伟, 陈鸿. 实验观测非厄米系统奇异点的手性翻转现象. , 2022, 71(13): 131101. doi: 10.7498/aps.71.20220842
[8]	陈海军, 任元, 王华. Bessel型光晶格中自旋-轨道耦合极化激元凝聚的稳态结构研究. , 2021, (): . doi: 10.7498/aps.70.20211949
[9]	张高见, 王逸璞. 腔光子-自旋波量子耦合系统中各向异性奇异点的实验研究. , 2020, 69(4): 047103. doi: 10.7498/aps.69.20191632
[10]	杨阳, 王安民, 曹连振, 赵加强, 逯怀新. 与XY双自旋链耦合的双量子比特系统的关联性与相干性. , 2018, 67(15): 150302. doi: 10.7498/aps.67.20180812
[11]	李雪琴, 赵云芳, 唐艳妮, 杨卫军. 基于金刚石氮-空位色心自旋系综与超导量子电路混合系统的量子节点纠缠. , 2018, 67(7): 070302. doi: 10.7498/aps.67.20172634
[12]	郑军, 李春雷, 杨曦, 郭永. 四端双量子点系统中的自旋和电荷能斯特效应. , 2017, 66(9): 097302. doi: 10.7498/aps.66.097302
[13]	方少寅, 陆海铭, 赖天树. 自旋极化度对GaAs量子阱中吸收饱和效应与载流子复合动力学的影响研究. , 2015, 64(15): 157201. doi: 10.7498/aps.64.157201
[14]	安兴涛, 穆惠英, 咸立芬, 刘建军. 量子点双链中电子自旋极化输运性质. , 2012, 61(15): 157201. doi: 10.7498/aps.61.157201
[15]	陈翔, 米贤武. 量子点腔系统中抽运诱导受激辐射与非谐振腔量子电动力学特性的研究. , 2011, 60(4): 044202. doi: 10.7498/aps.60.044202
[16]	潘靖, 周岚, 胡经国. 交换偏置系统中的反铁磁磁化与自旋波. , 2009, 58(9): 6487-6493. doi: 10.7498/aps.58.6487
[17]	李晓奇, 王剑, 王飞, 胡响明. 非旋波耦合条件下微波控制的光学双稳与多稳. , 2008, 57(4): 2236-2241. doi: 10.7498/aps.57.2236
[18]	张雅男, 晏世雷. 随机横场与晶场作用混合自旋系统的热力学性质. , 2003, 52(11): 2890-2895. doi: 10.7498/aps.52.2890
[19]	赛·萨楚尔夫, 胡岗. 劣腔情况失谐双光子光学双稳系统的原子压缩效应. , 1992, 41(4): 578-586. doi: 10.7498/aps.41.578
[20]	张林, 林仁明. 良腔情况吸收与色散混合受驱动光学系统多光子过程压缩效应. , 1990, 39(11): 1714-1720. doi: 10.7498/aps.39.1714

计量

文章访问数: 8714
PDF下载量: 246
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

腔自旋波混合系统的研究进展