-
以单层MoS2为代表的二维过渡金属硫族化物, 因具有可调谐的非零带隙, 故应用在光电子学器件中要比石墨烯更具优势. 本文使用经典电磁理论和有限元分析方法, 研究了谐振腔中腔模与单层MoS2等离激元之间耦合形成的腔耦合等离极化激元, 并重点计算和验证了其中高阶模式的特性. 考虑到化学气相沉积法生长的单层MoS2中衬底、多晶和缺陷会引起弱电子局域化, 从而导致基于自由电子气假设的Drude模型准确性变差, 故本文在理论和仿真中使用了Drude-Smith模型描述单层MoS2光电导率, 该模型通过拟合实验数据得到. 基于此, 不仅导出了高阶腔耦合等离极化激元的色散方程, 并求解出了其色散曲线, 还通过仿真计算验证了这些高阶模式的存在性, 分析了其基本性质以及弱电子局域化的影响. 上述结果能加深对二维材料等离激元的耦合激发以及特性调控的理解, 所用理论模型也能推广到其他低维、拓扑量子材料相关的等离系统当中.Compared with graphene, two-dimensional (2D) transition metal sulfides, represented by mono-/few-layer MoS2, have tunable non-zero bandgap, and thus their applications in optoelectronic devices are more advantageous. By using classical electromagnetic theory and finite element method (FEM), we investigate the cavity coupled plasmon polaritons (CCPPs) formed through the coupling between cavity modes in a resonator and plasmons in monolayer MoS2, particularly calculate and verify the properties of the high-order CCPPs. In previous work, it was demonstrated that the substrates, defects, and polycrystalline grains of the CVD grown monolayer MoS2 usually induce weak electron localization, which leads to the deviation from the Drude model based on the approximation of free electron gas. Therefore, here we use the Drude-Smith model with characteristic parameters obtained experimentally to describe the optical conductivity of monolayer MoS2 in our theoretical calculation and simulation. Then, we not only derive and solve the dispersion equations of the high-order CCPPs, but also verify the existence and analyze the properties of these high-order modes. Specifically, there are three types of CCPPs in the asymmetric cavity-monolayer MoS2 system, i.e. the FP-like-modes (FPLMs), the surface-plasmon-like modes (SPLMs), and the quasi-localized modes (QLMs). Among them, the FPLMs and QLMs can support high-order modes whereas the SPLMs only support the fundamental modes. According to our model, we calculate the wave localization properties for the 7th-order and 8th-order FPLM, the 3rd-order and 6th-order QLM, and the SPLM. These theoretical results are in good agreement with the simulation results. Moreover, the effects of weak electron localization are also shown by comparing the field distributions of the CCPPs based on the Drude model with those based on the Drude-Smith model. It is found that weak electron localization can reduce the coupling between the cavity modes and the plasmons in monolayer MoS2. These results can deepen our understanding of the excitation of plasmons in 2D materials as well as the modulation of their properties. Furthermore, the theoretical model can also be extended to other plasmonic systems related to low-dimensional and topological quantum materials.
-
Keywords:
- plasmons /
- monolayer MoS2 /
- cavity /
- terahertz
[1] Novoselov K S, Geim A K, Morozov S V, Jiang D, Zhang Y, Dubonos S V, Grigorieva I V, Firsov A A 2004 Science 306 666
Google Scholar
[2] Geim A K, Novoselov K S 2007 Nat. Mater. 6 183
Google Scholar
[3] Fan Y C, Shen N H, Zhang F L, Zhao Q, Wu H J, Fu Q H, Wei Z Y, Li H Q, Soukoulis C M 2019 Adv. Opt. Mater. 7 1800537
Google Scholar
[4] Lu W, Ling J W, Xiu F X, Sun D 2018 Phys. Rev. B 98 104310
Google Scholar
[5] Hou L, Yang Y K, Li A L, Wang Q J, Li Q N, Wu M, Ji P C, Zhang Y J, Xiao Y M, Xu W, Xiu F X, Ding L 2023 Phys. Rev. B 108 115416
Google Scholar
[6] Mak K F, Lee C, Hone J, Shan J, Heinz T F 2010 Phys. Rev. Lett. 105 136805
Google Scholar
[7] Wang Q H, Kalantar-Zadeh K, Kis A, Coleman J N, Strano M S 2012 Nat. Nanotechnol. 7 699
Google Scholar
[8] Manzeli S, Ovchinnikov D, Pasquier D, Yazyev O V, Kis A 2017 Nat. Rev. Mater. 2 17033
Google Scholar
[9] Liu X, Hou L, Ji P C, Wang Q J, Wu M, Xiao Y M, Xu W, Ding L 2023 Nanophotonics 12 4441
Google Scholar
[10] Liu H, Neal A T, Zhu Z, Luo Z, Xu X F, Tomanek D, Ye P D 2014 ACS Nano 8 4033
Google Scholar
[11] Qiao J, Kong X, Hu Z X, Yang F, Ji W 2014 Nat. Commun. 5 4475
Google Scholar
[12] Zhang S J, Pei Y F, Hu S Q, Wu N, Chen D Q, Lian C, Meng S 2023 Chin. Phys. Lett. 40 077502
Google Scholar
[13] Liu X Z, Galfsky T, Sun Z, Xia F N, Lin E C, Lee Y H, Kena-Cohen S, Menon V M 2015 Nat. Photonics 9 30
Google Scholar
[14] Kleemann M E, Chikkaraddy R, Alexeev E M, Kos D, Carnegie C, Deacon W, Pury A C de, Grosse C, Nijs B de, Mertens J, Tartakovskii A I, Baumberg J J 2017 Nat. Commun. 8 1296
Google Scholar
[15] Verre R, Baranov D G, Munkhbat B, Cuadra J, Kall M, Shegai T 2019 Nat. Nanotechnol. 14 679
Google Scholar
[16] Liu W J, Lee B, Naylor C H, Ee H S, Park J, Johnson A T C, Agarwal R 2016 Nano Lett. 16 1262
Google Scholar
[17] Hu G W, Krasnok A, Mazor Y, Qu C W, Alu A 2020 Nano Lett. 20 3217
Google Scholar
[18] Sun B, Wang Z, Liu Z, Tan X, Liu X, Shi T, Zhou J, Liao G 2019 Adv. Funct. Mater. 29 1900541
Google Scholar
[19] Leng Q, Su H, Liu J, Zhou L, Qin K, Wang Q, Fu J, Wu S, Zhang X 2021 Nanophotonics 10 1871
Google Scholar
[20] Lan H Y, Hsieh Y H, Chiao Z Y, Jariwala D, Shih M H, Yen T J, Hess O, Lu Y J 2021 Nano Lett. 21 3083
Google Scholar
[21] Petrić M M, Kremser M, Barbone M, Nolinder A, Lyamkina A, Stier A V, Kaniber M, Müller K, Finley J J 2022 Nano Lett. 22 561
Google Scholar
[22] Zhu Y X, Yang J W, Abad-Arredondo J, Fernández-Domínguez A I, Garcia-Vidal F J, Natelson D 2024 Nano Lett. 24 525
Google Scholar
[23] Wang C, Xu W, Mei H Y, Qin H, Zhao X N, Zhang C, Yuan H F, Zhang J, Xu Y, Li P, Li M 2019 Opt. Lett. 44 4139
Google Scholar
[24] Liu J, Ding L, Zhao C X, Liang C N, Xiao Y M, Zhang J, Xu W 2019 IEEE Photonics J. 11 4800608
[25] Guo T Y, Hou L, Xu W, Xiao Y M, Ding L 2022 J. Opt. Soc. Am. B: Opt. Phys. 39 1711
Google Scholar
[26] Ding L, Xu W, Zhao C, Wang S, Liu H 2015 Opt. Lett. 40 4524
Google Scholar
[27] Maier S A 2007 Plasmonics: Fundamentals and Applications (New York: Springer) p21
-
图 1 非对称谐振腔-单层MoS2系统结构示意图
Fig. 1. Diagram of the asymmetric cavity-monolayer MoS2 system.
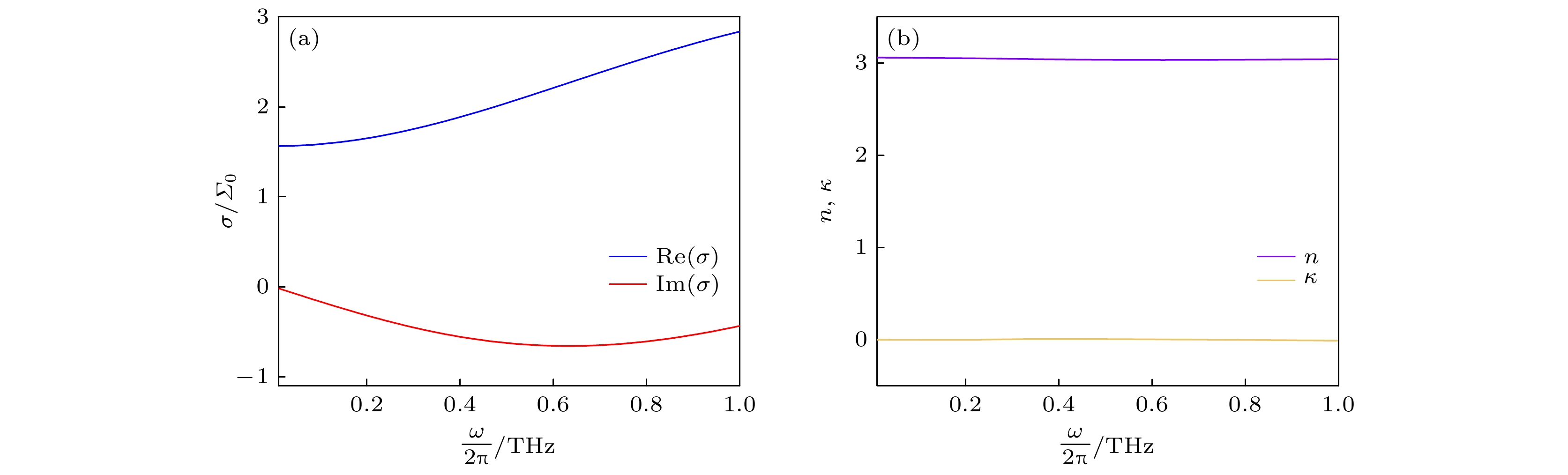
图 2 (a) 单层MoS2光电导率随频率的变化; (b) 蓝宝石衬底的复折射率随频率的变化. 图(a)中使用普适电导率$\varSigma_0 = e^2/4 \hbar $对光电导率实部和虚部做归一化
Fig. 2. (a) Frequency dependency of optical conductivity of monolayer MoS2; (b) frequency dependency of the complex refractive index of the sapphire substrate. In panel (a) both the real and imaginary parts of the optical conductivity are normalized by universal conductivity $\varSigma_0 = e^2/4 \hbar $.
图 3 (a) 非对称谐振腔等离系统中CCPP的色散关系图; (b) FPLM, (c) QLM和(d) SPLM模式的局域程度
Fig. 3. (a) Dispersion relations of the CCPPs supported by the ACPS and the localization of (b) FPLM, (c) QLM, and (d) SPLM modes.
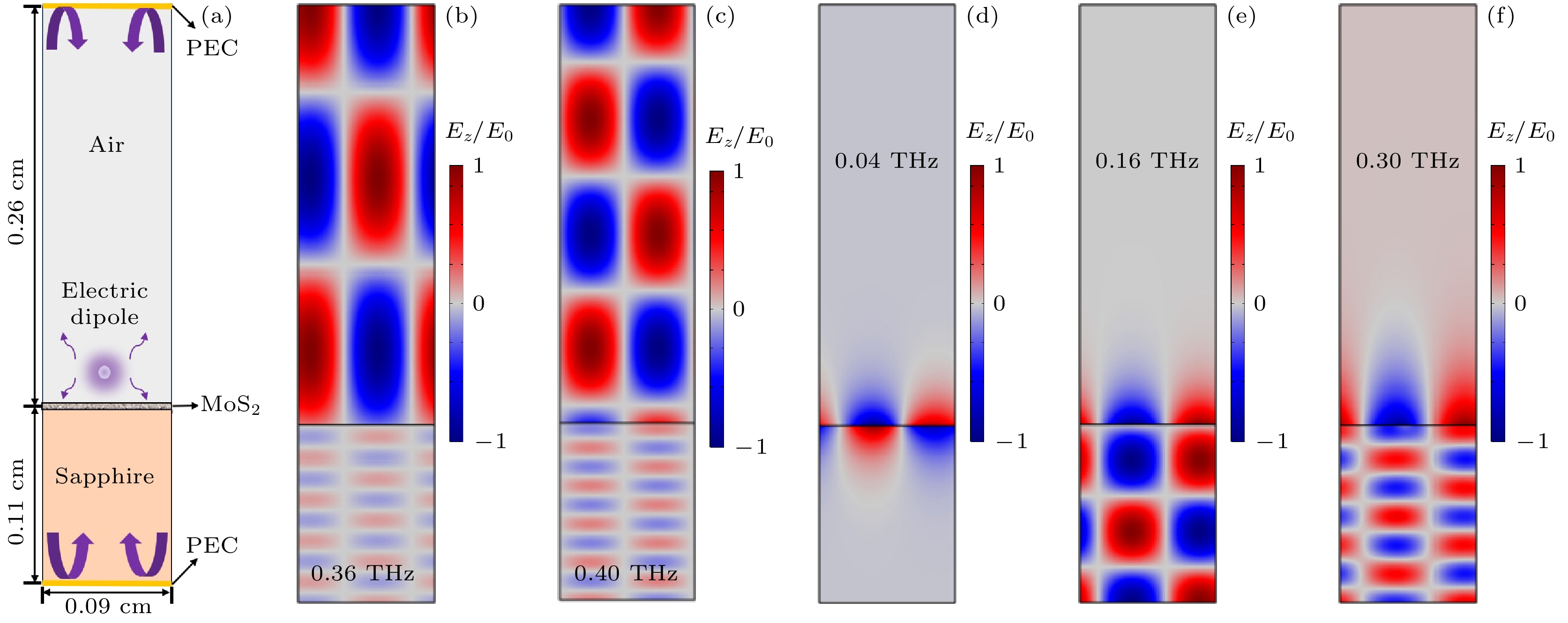
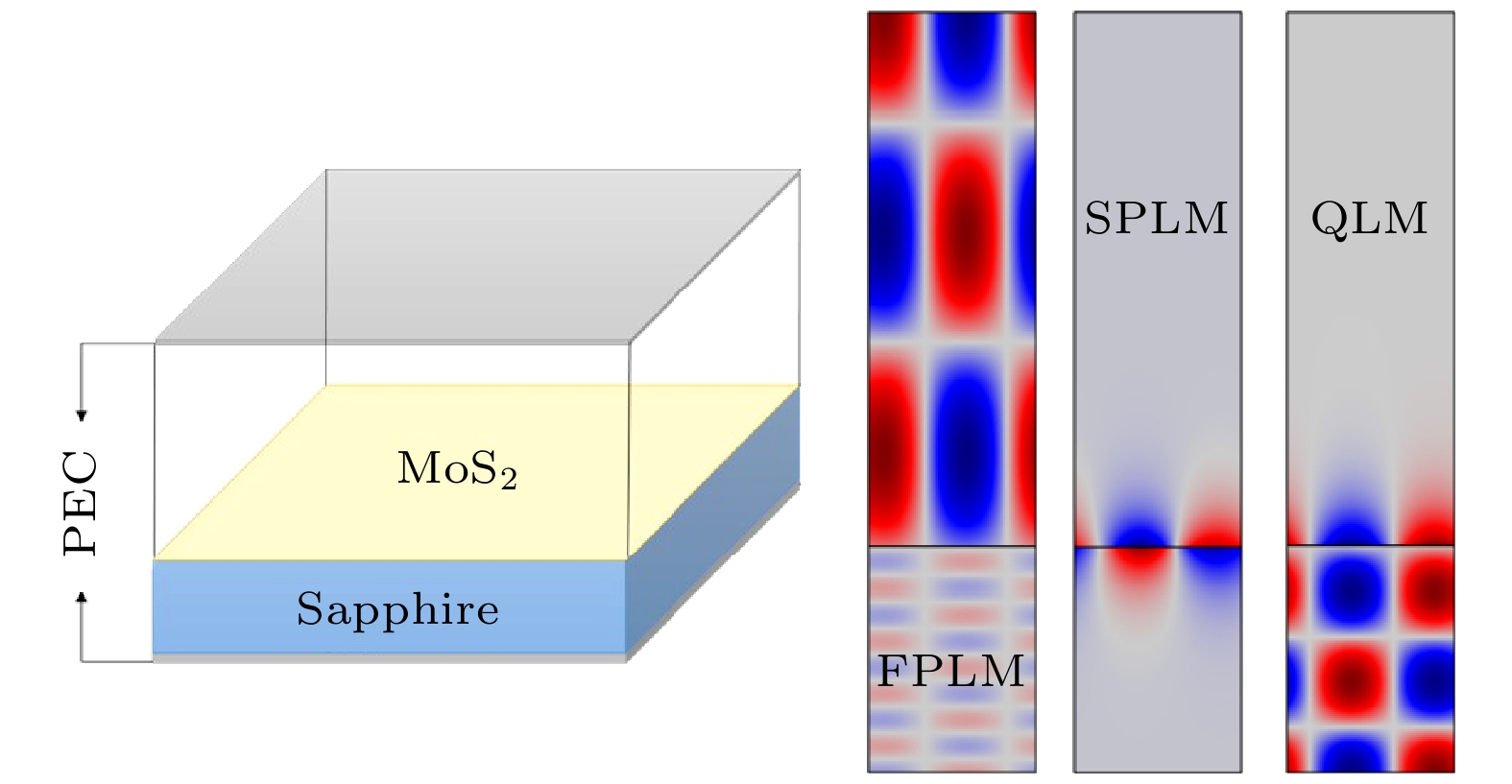
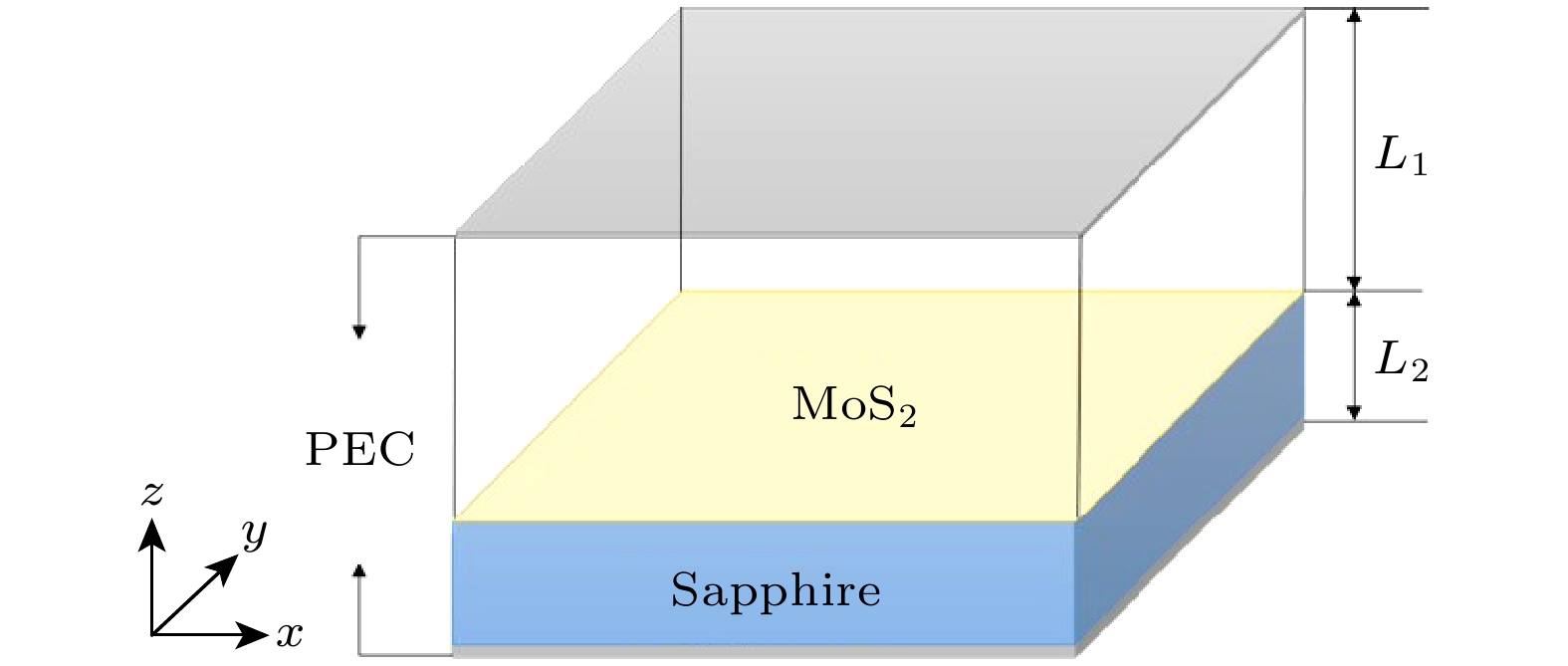
图 4 CCPP的FEM模拟 (a) 模拟模型示意图; (b) NF = 7和(c) NF = 8时FPLM, (d) 基模SPLM以及(e) NQ = 3和(f) NQ = 6时QLM的电磁场Ez空间分布. 注意此处电场分量Ez都已使用各自的最大值E0做了归一化
Fig. 4. FEM simulation results of the CCPPs: (a) Diagram of the simulation model. Field distributions of Ez for the FPLMs of (b) NF = 7 and (c) NF = 8, (d) the fundamental mode of SPLM, and the QLMs of (e) NQ = 3 and (f) NQ = 6. Note that the fields Ez are normalized by the corresponding maximum values E0.
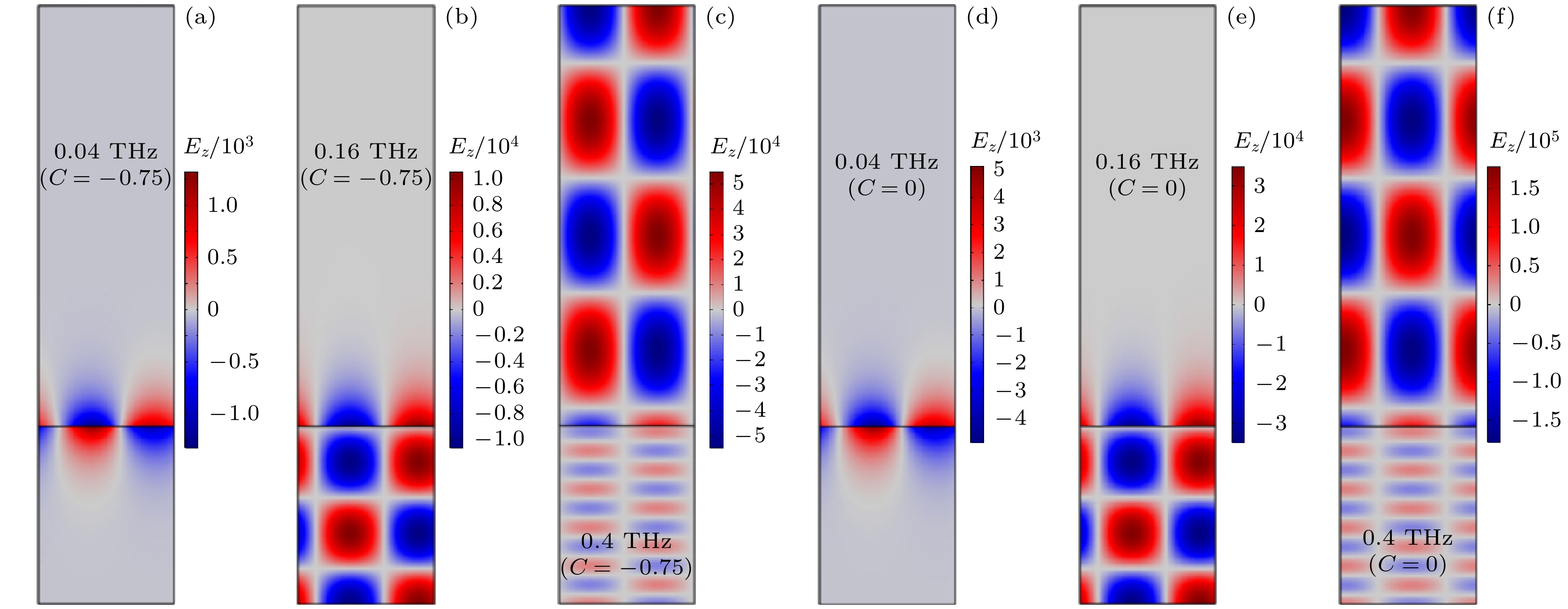
图 5 局域因子C不同时, CCPP的FEM模拟 (a)—(c) C = –0.75时的SPLM (a), QLM (b)及FPLM (c); (d)—(f) C = 0 时的SPLM (d), QLM (e)及FPLM (f). 注意此处电场分量Ez都未做归一化
Fig. 5. FEM simulation results of the CCPPs with different C: (a)–(c) Field distributions of (a) SPLM, (b) QLM, and (c) FPLM for C = –0.75; (d)–(f) results of (d) SPLM, (e) QLM, and (f) FPLM for C = 0. Note that the fields Ez are not normalized.
-
[1] Novoselov K S, Geim A K, Morozov S V, Jiang D, Zhang Y, Dubonos S V, Grigorieva I V, Firsov A A 2004 Science 306 666
Google Scholar
[2] Geim A K, Novoselov K S 2007 Nat. Mater. 6 183
Google Scholar
[3] Fan Y C, Shen N H, Zhang F L, Zhao Q, Wu H J, Fu Q H, Wei Z Y, Li H Q, Soukoulis C M 2019 Adv. Opt. Mater. 7 1800537
Google Scholar
[4] Lu W, Ling J W, Xiu F X, Sun D 2018 Phys. Rev. B 98 104310
Google Scholar
[5] Hou L, Yang Y K, Li A L, Wang Q J, Li Q N, Wu M, Ji P C, Zhang Y J, Xiao Y M, Xu W, Xiu F X, Ding L 2023 Phys. Rev. B 108 115416
Google Scholar
[6] Mak K F, Lee C, Hone J, Shan J, Heinz T F 2010 Phys. Rev. Lett. 105 136805
Google Scholar
[7] Wang Q H, Kalantar-Zadeh K, Kis A, Coleman J N, Strano M S 2012 Nat. Nanotechnol. 7 699
Google Scholar
[8] Manzeli S, Ovchinnikov D, Pasquier D, Yazyev O V, Kis A 2017 Nat. Rev. Mater. 2 17033
Google Scholar
[9] Liu X, Hou L, Ji P C, Wang Q J, Wu M, Xiao Y M, Xu W, Ding L 2023 Nanophotonics 12 4441
Google Scholar
[10] Liu H, Neal A T, Zhu Z, Luo Z, Xu X F, Tomanek D, Ye P D 2014 ACS Nano 8 4033
Google Scholar
[11] Qiao J, Kong X, Hu Z X, Yang F, Ji W 2014 Nat. Commun. 5 4475
Google Scholar
[12] Zhang S J, Pei Y F, Hu S Q, Wu N, Chen D Q, Lian C, Meng S 2023 Chin. Phys. Lett. 40 077502
Google Scholar
[13] Liu X Z, Galfsky T, Sun Z, Xia F N, Lin E C, Lee Y H, Kena-Cohen S, Menon V M 2015 Nat. Photonics 9 30
Google Scholar
[14] Kleemann M E, Chikkaraddy R, Alexeev E M, Kos D, Carnegie C, Deacon W, Pury A C de, Grosse C, Nijs B de, Mertens J, Tartakovskii A I, Baumberg J J 2017 Nat. Commun. 8 1296
Google Scholar
[15] Verre R, Baranov D G, Munkhbat B, Cuadra J, Kall M, Shegai T 2019 Nat. Nanotechnol. 14 679
Google Scholar
[16] Liu W J, Lee B, Naylor C H, Ee H S, Park J, Johnson A T C, Agarwal R 2016 Nano Lett. 16 1262
Google Scholar
[17] Hu G W, Krasnok A, Mazor Y, Qu C W, Alu A 2020 Nano Lett. 20 3217
Google Scholar
[18] Sun B, Wang Z, Liu Z, Tan X, Liu X, Shi T, Zhou J, Liao G 2019 Adv. Funct. Mater. 29 1900541
Google Scholar
[19] Leng Q, Su H, Liu J, Zhou L, Qin K, Wang Q, Fu J, Wu S, Zhang X 2021 Nanophotonics 10 1871
Google Scholar
[20] Lan H Y, Hsieh Y H, Chiao Z Y, Jariwala D, Shih M H, Yen T J, Hess O, Lu Y J 2021 Nano Lett. 21 3083
Google Scholar
[21] Petrić M M, Kremser M, Barbone M, Nolinder A, Lyamkina A, Stier A V, Kaniber M, Müller K, Finley J J 2022 Nano Lett. 22 561
Google Scholar
[22] Zhu Y X, Yang J W, Abad-Arredondo J, Fernández-Domínguez A I, Garcia-Vidal F J, Natelson D 2024 Nano Lett. 24 525
Google Scholar
[23] Wang C, Xu W, Mei H Y, Qin H, Zhao X N, Zhang C, Yuan H F, Zhang J, Xu Y, Li P, Li M 2019 Opt. Lett. 44 4139
Google Scholar
[24] Liu J, Ding L, Zhao C X, Liang C N, Xiao Y M, Zhang J, Xu W 2019 IEEE Photonics J. 11 4800608
[25] Guo T Y, Hou L, Xu W, Xiao Y M, Ding L 2022 J. Opt. Soc. Am. B: Opt. Phys. 39 1711
Google Scholar
[26] Ding L, Xu W, Zhao C, Wang S, Liu H 2015 Opt. Lett. 40 4524
Google Scholar
[27] Maier S A 2007 Plasmonics: Fundamentals and Applications (New York: Springer) p21
下载:
计量
- 文章访问数: 289
- PDF下载量: 16
- 被引次数: 0
