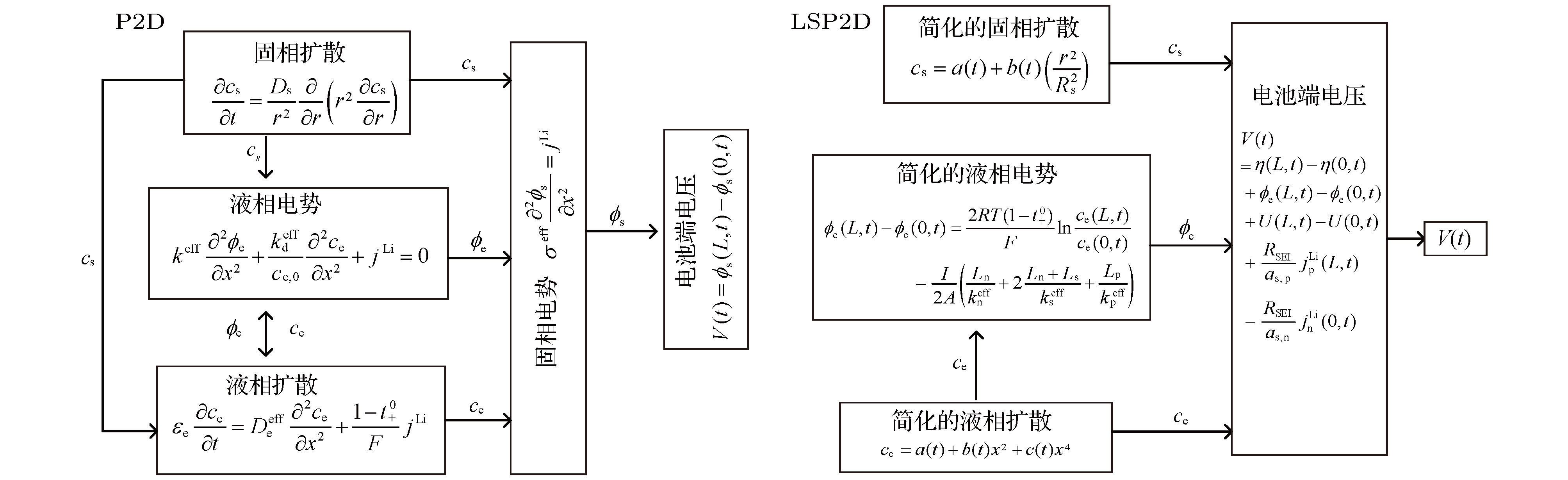
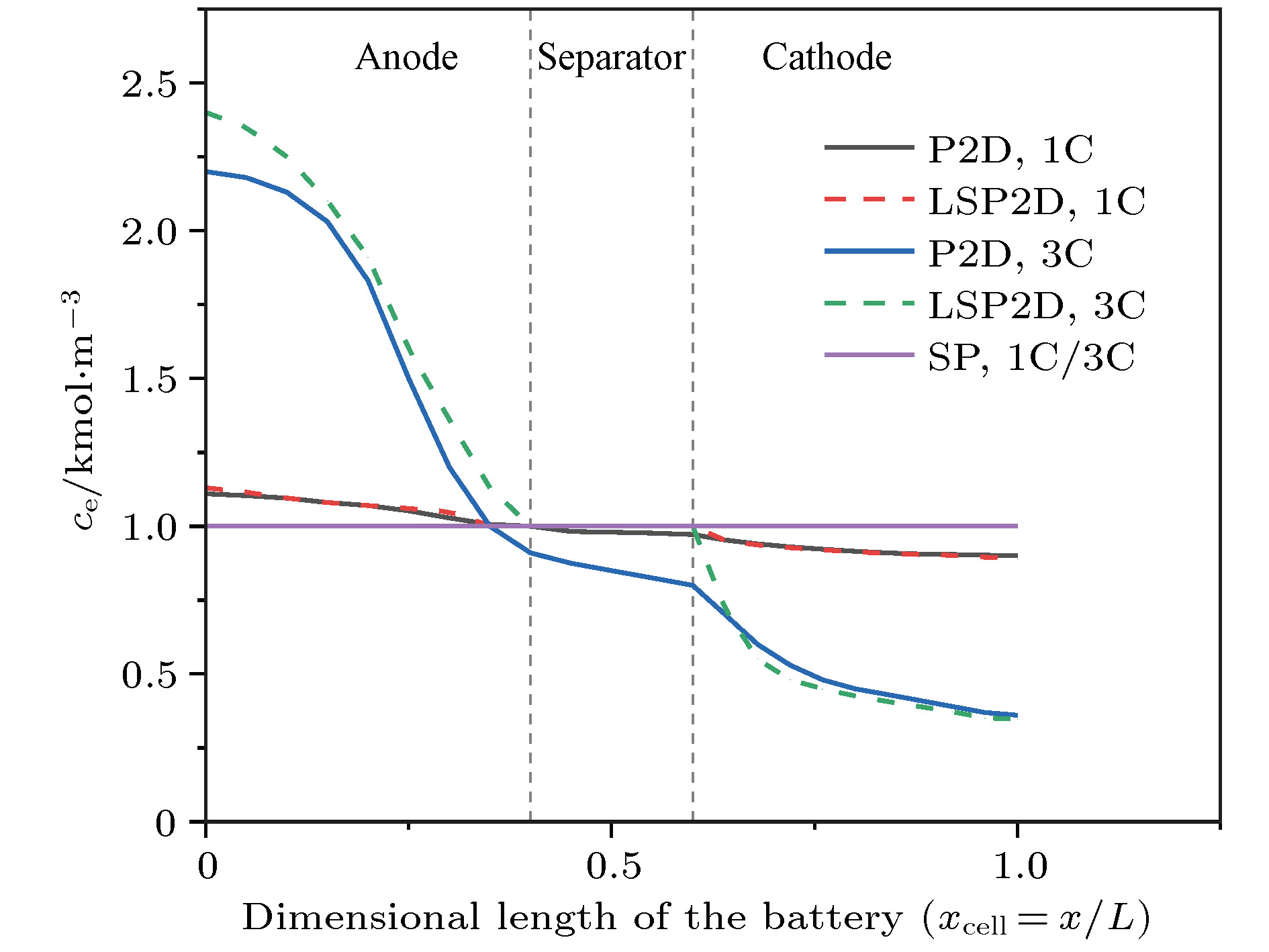
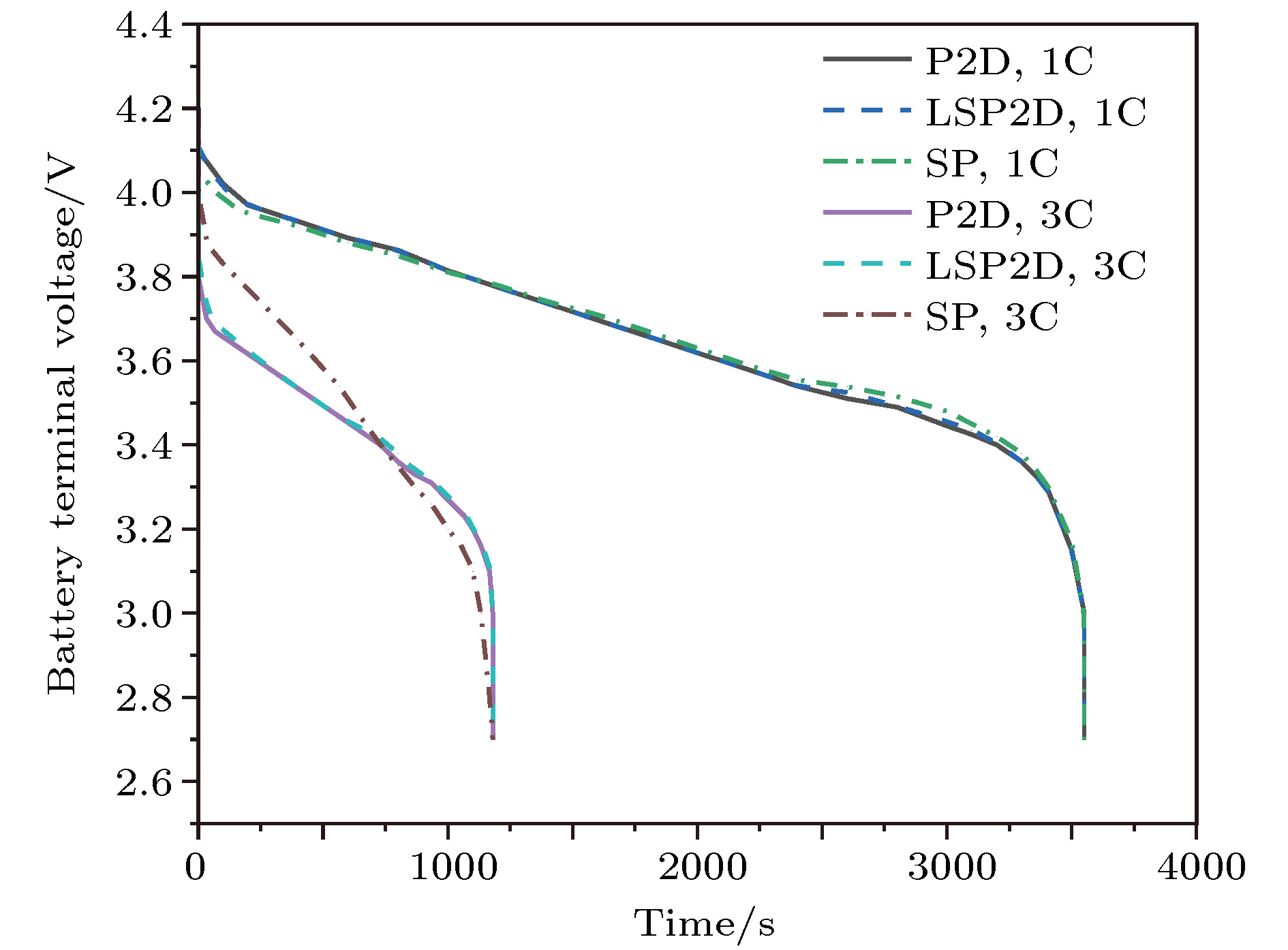
-
锂离子电池的电化学模型对于电池特性分析和电池管理具有重要意义, 但是准二维(P2D)模型复杂度太高, 为了在保证模型精度的基础上尽量降低复杂度, 本文提出了一种包含液相简化的P2D (LSP2D)模型, 该模型首先基于电化学平均动力学将电池端电压化简成为仅耦合固相Li+浓度cs和液相Li+浓度ce的方程, 然后进一步对表达cs和ce演化规律的偏微分方程进行抛物线近似化简, 使得最终的模型由多项式组成. COMSOL仿真表明在放电倍率为1C时该模型与单粒子(SP)模型的估算精度和速度相当, 但在放电倍率为3C时, 该模型的估算时间比P2D模型减少了99.73%, 与SP模型相当, 估算精度相比SP模型有大幅度提升.The pseudo-two-dimensional (P2D) model is the most widely used electrochemical model for lithium-ion batteries. Because of the complexity and the difficulty in using the complete P2D model, many simplified P2D models, such as the single particle model (SP model) and the parabolic profile approximation model (PP model), have been proposed. However, the using of the SP model can cause a large amount of precision to lose in its simplified process, while the PP model has a high complexity. In this paper, we propose a liquid phase simplification P2D (LSP2D) model. The using of the LSP2D model has a small precision loss and a relatively low complexity. The LSP2D model is based on the electrochemical average kinetics of the lithium ion battery. We first simplify the terminal voltage into an equation containing only the solid phase concentration cs and the liquid phase concentration ce. Then we use the partial differential equation to represent the solid phase concentration cs and the liquid phase concentration ce, and then obtain a final model. The simulation environment is based on COMSOL, and the simulation results show that when the discharge rate is 1C, the estimation accuracy and speed from the LSP2D model are similar to those from the SP model. But when the discharge rate is 3C, the estimation time from the LSP2D model is reduced by 99.73% compared with that from the P2D model, and the estimation accuracy is greatly improved compared with the estimation accuracy from the SP model.
-
Keywords:
- electrochemical model /
- battery management system /
- liquid phase diffusion equation /
- parabolic approximation
[1] Zou C F, Manzie C, Nešic D 2016 IEEE Trans. Control Syst. Technol. 24 1594
Google Scholar
[2] Seaman A, Dao T S, McPhee J 2014 J. Power Sources 256 410
Google Scholar
[3] Tang S X, Solorio L C, Wang Y, Krstic M 2017 Automatica 83 206
Google Scholar
[4] 庞辉 2018 67 058201
Google Scholar
Pang H 2018 Acta Phys. Sin. 67 058201
Google Scholar
[5] Hu L B, Choi J W, Yang Y, Jeong S, Mantia F L, Cui L F, Cui Y 2009 Proc. Natl. Acad. Sci. 106 51
Google Scholar
[6] Lindgren J, Asghar I, Lund P D 2016 Int. J. Energy Res. 40 1576
Google Scholar
[7] Bizeray A M, Kim J H, Duncan S R, Howey D A 2018 IEEE Trans. Control Syst. Technol.
Google Scholar
[8] Doyle M, Fuller T F, Newman J 1993 J. Electrochem. Soc. 140 1526
Google Scholar
[9] Li J, Lotfi N, Landers R G, Park J 2017 J. Electrochem. Soc. 164 A874
Google Scholar
[10] Tanim T R, Rahn C D, Wang C Y 2015 J. Dyn. Syst. Meas. Contr. 137 011005
Google Scholar
[11] Subramanian V R, Diwakar V D, Tapriyal D 2005 J. Electrochem. Soc. 152 A2002
Google Scholar
[12] 程昀, 李劼, 贾明, 汤依伟, 杜双龙, 艾立华, 殷宝华, 艾亮 2015 64 210202
Google Scholar
Cheng Y, Li J, Jia M, Tang Y W, Du S L, Ai L H, Yin B H, Ai L 2015 Acta Phys. Sin. 64 210202
Google Scholar
[13] Santhanagopalan S, Guo Q Z, Ramadass P, White R E 2006 J. Power Sources 156 620
Google Scholar
[14] Farag M, Fleckenstein M, Habibi S 2017 J. Power Sources 342 351
Google Scholar
[15] Zheng L F, Zhang L, Zhu J G, Wang G X, Jiang J C 2016 Appl. Energy 180 424
Google Scholar
[16] 庞辉 2017 66 238801
Google Scholar
Pang H 2017 Acta Phys. Sin. 66 238801
Google Scholar
[17] Prada E, Di-Domenico D, Creff Y, Bernard J, Sauvant-Moynot V, Huet F 2012 J. Electrochem. Soc. 159 A1508
Google Scholar
[18] Han X B, Ouyang M G, Lu L G, Li J Q 2015 J. Power Sources 278 814
Google Scholar
[19] Dawson-Elli N, Lee S B, Pathak M 2018 J. Electrochem. Soc. 165 A1
Google Scholar
[20] Ramadass P, Haran B, Gomadam P M, 2004 J. Electrochem. Soc. 151 A196
Google Scholar
-
图 3 1C和3C放电率下, SP, LSP2D和P2D模型得到的放电末期液相Li+浓度
${c_{\rm{e}}}$ 比较Fig. 3. Comparison of liquid phase Li+ concentration
${c_{\rm{e}}}$ obtained by SP, LSP2D and P2D model at 1C and 3C discharge rates.
图 4 三种模型在放电率为1C和3C时的放电曲线
Fig. 4. Discharge curves of three models at 1C and 3C discharge rates.
表 1 各参数的值
Table 1. Values of parameters.
${a_1}$ ${b_1}$ ${c_1}$ ${a_2}$ ${b_2}$ ${a_3}$ ${b_3}$ ${c_3}$ $\displaystyle\frac{1}{8} + \alpha \tau $ $\displaystyle\frac{{15}}{4}$ $ - \displaystyle\frac{{15}}{8}$ $1$ 0 1 $\displaystyle\frac{{30}}{7}\beta \tau $ $ - \displaystyle\frac{{15}}{7}\beta \tau $ 
下载: 导出CSV
表 2 锂离子电池参数表
Table 2. Parameters lists of Li-ion battery.
Symbol Anode Cathode Separator $\sigma$/S·m–1 100 100 ${\varepsilon _{\rm s}}$ 0.49 0.59 ${\varepsilon _{\rm e}}$ 0.485 0.365 0.724 Brug 4.0 4.0 4.0 ${c_{{\rm{e,0}}}}$/mol·m–3 1000 1000 1000 ${c_{{\rm{s,0}}}}$/mol·m–3 916.65 48977.25 ${c_{{\rm{s,max}}}}$/mol·m–3 30555 51555 A/m2 $6.03 \!\times\! {10^{ - 4}}$ $5.31 \!\times\! {10^{ - 4}}$ ${D_{\rm{e}}}$/m2·s–1 $7.5 \!\times\! {10^{ - 10}}$ $7.5 \!\times\! {10^{ - 10}}$ $7.5 \!\times\! {10^{ - 10}}$ ${D_{\rm{s}}}$/m2·s–1 $3.9 \!\times\! {10^{ - 14}}$ $1.0 \!\times\! {10^{ - 14}}$ k/mol·(mol·m–3)–1.5 $4.854 \!\times\! {10^{ - 6}}$ $2.252 \!\times\! {10^{ - 6}}$ ${R_{\rm{s}}}$/m $2 \!\times\! {10^{ - 6}}$ $2 \!\times\! {10^{ - 6}}$ x/m $8.8 \!\times\! {10^{ - 5}}$ $8.0 \!\times\! {10^{ - 5}}$ $8.0 \!\times\! {10^{ - 5}}$ ${R_{{\rm{SEI}}}}/\Omega$·m–2 0.01 I/A·m–2 20 $\alpha $ 0.5 0.5 F/C·mol 96487 R/J·mol·K–1 8.314 T/K 298.15
下载: 导出CSV
表 3 放电率为1C和3C时三种模型估算电池端电压的平均误差
Table 3. Average error of the battery terminal voltage is estimated by three models when the discharge rate is 1C and 3C.
Model Average error at
discharge rate 1C/VAverage error at
discharge rate 3C/VP2D 0 0 LSP2D 0.0056 0.014 SP 0.0052 0.142
下载: 导出CSV
表 4 比较三种模型估算速度
Table 4. Comparison of the estimated speeds of the three models.
Model Time for 50 cycles/s P2D 7860 LSP2D 21 SP 12
下载: 导出CSV
-
[1] Zou C F, Manzie C, Nešic D 2016 IEEE Trans. Control Syst. Technol. 24 1594
Google Scholar
[2] Seaman A, Dao T S, McPhee J 2014 J. Power Sources 256 410
Google Scholar
[3] Tang S X, Solorio L C, Wang Y, Krstic M 2017 Automatica 83 206
Google Scholar
[4] 庞辉 2018 67 058201
Google Scholar
Pang H 2018 Acta Phys. Sin. 67 058201
Google Scholar
[5] Hu L B, Choi J W, Yang Y, Jeong S, Mantia F L, Cui L F, Cui Y 2009 Proc. Natl. Acad. Sci. 106 51
Google Scholar
[6] Lindgren J, Asghar I, Lund P D 2016 Int. J. Energy Res. 40 1576
Google Scholar
[7] Bizeray A M, Kim J H, Duncan S R, Howey D A 2018 IEEE Trans. Control Syst. Technol.
Google Scholar
[8] Doyle M, Fuller T F, Newman J 1993 J. Electrochem. Soc. 140 1526
Google Scholar
[9] Li J, Lotfi N, Landers R G, Park J 2017 J. Electrochem. Soc. 164 A874
Google Scholar
[10] Tanim T R, Rahn C D, Wang C Y 2015 J. Dyn. Syst. Meas. Contr. 137 011005
Google Scholar
[11] Subramanian V R, Diwakar V D, Tapriyal D 2005 J. Electrochem. Soc. 152 A2002
Google Scholar
[12] 程昀, 李劼, 贾明, 汤依伟, 杜双龙, 艾立华, 殷宝华, 艾亮 2015 64 210202
Google Scholar
Cheng Y, Li J, Jia M, Tang Y W, Du S L, Ai L H, Yin B H, Ai L 2015 Acta Phys. Sin. 64 210202
Google Scholar
[13] Santhanagopalan S, Guo Q Z, Ramadass P, White R E 2006 J. Power Sources 156 620
Google Scholar
[14] Farag M, Fleckenstein M, Habibi S 2017 J. Power Sources 342 351
Google Scholar
[15] Zheng L F, Zhang L, Zhu J G, Wang G X, Jiang J C 2016 Appl. Energy 180 424
Google Scholar
[16] 庞辉 2017 66 238801
Google Scholar
Pang H 2017 Acta Phys. Sin. 66 238801
Google Scholar
[17] Prada E, Di-Domenico D, Creff Y, Bernard J, Sauvant-Moynot V, Huet F 2012 J. Electrochem. Soc. 159 A1508
Google Scholar
[18] Han X B, Ouyang M G, Lu L G, Li J Q 2015 J. Power Sources 278 814
Google Scholar
[19] Dawson-Elli N, Lee S B, Pathak M 2018 J. Electrochem. Soc. 165 A1
Google Scholar
[20] Ramadass P, Haran B, Gomadam P M, 2004 J. Electrochem. Soc. 151 A196
Google Scholar
下载:
计量
- 文章访问数: 13884
- PDF下载量: 338
- 被引次数: 0
