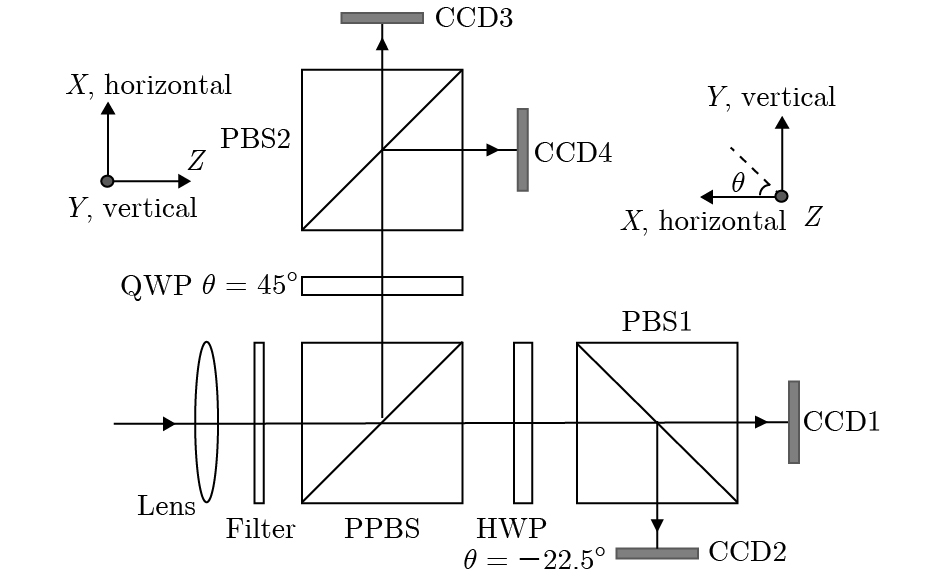
-
分振幅型全Stokes同时偏振成像仪具有实时性好、空间分辨率高、精度高等优点, 有很高的应用价值. 分振幅型全Stokes同时偏振成像系统利用偏振分束器、1/2波片和1/4波片将入射光Stokes矢量调制在4幅图像中, 可解析入射光Stokes矢量. 1/2波片和1/4波片的相位延迟误差对Stokes矢量测量精度有着不可忽略的影响. 建立了包含上述两种误差的Stokes矢量测量误差方程, 分析了1/2波片和1/4波片相位延迟耦合误差对自然光、0°/45°线偏光、左旋圆偏光等典型基态入射光的Stokes矢量测量误差的影响, 推导了任意偏振态的Stokes矢量测量误差的表征方法. 在邦加球球面和球内选取不同偏振度的Stokes矢量作为入射光进行仿真. 结果表明, Stokes矢量测量误差和偏振度测量误差均随着入射光偏振度的增大而增大. 选取入射光偏振度为1时的偏振测量精度评估系统. 为满足2%的偏振测量精度, 1/2波片相位延迟误差应在±1.6°内, 1/4波片相位延迟误差应在±0.5°内. 这对提高系统的偏振测量精度具有重要意义, 为系统设计和研制提供了重要的理论指导.The division-of-amplitude full Stokes simultaneous polarization imaging system has prominent merits, such as real time, high spatial resolution, high precision, etc. The development of the division-of-amplitude full Stokes simultaneous polarization imaging system has a high application value. The division-of-amplitude full Stokes simultaneous polarization imaging system uses polarization beam splitters, a half wave plate (HWP) and a quarter wave plate (QWP) to modulate the incident Stokes vector into four intensity images. Using the four intensity images, the incident Stokes vector can be analyzed. In the system, the phase delay errors of the HWP and the QWP have a direct influence on the measurement accuracy of the incident Stokes vector. A Stokes vector measurement error equation containing the phase delay errors of the HWP and the QWP is established. When there are the phase delay errors of the HWP and the QWP in the system, the Stokes vector measurement errors of the unpolarized light, 0° liner polarized light, 90° liner polarized light, 45° liner polarized light, 135° liner polarized light, right circularly polarized light and left circularly polarized light are analyzed. A method of solving the Stokes vector measurement error of incident light with any polarization state is given. When the Stokes vectors with different degrees of polarization (DOPs) are used as the incident light, the simulation results show that both the Stokes vector measurement error and the DOP measurement error increase with the DOP of incident light increasing. Therefore, we select the polarization measurement accuracy to evaluate the system when the DOP of incident light equals 1. To ensure that the polarization measurement accuracy of the system is within 2%, the phase delay error of the HWP should be within ±1.6° and the phase delay error of the QWP should be within ±0.5°. The analysis results of the phase delay errors of the HWP and the QWP are of great significance for improving the polarization measurement accuracy of the division-of-amplitude full Stokes simultaneous polarization imaging system, and also provide important theoretical guidance in designing and developing the system.
-
Keywords:
- polarization imaging /
- wave plate /
- phase delay error /
- Stokes vector
[1] Zhao H J, Xu W J 2016 Sensors 16 1223
Google Scholar
[2] 韩平丽, 刘飞, 张广, 陶禹, 邵晓鹏 2018 67 054202
Han P L, Liu F, Zhang G, Tao Y, Shao X P 2018 Acta Phys. Sin. 67 054202
[3] Teimuraz K, Giorgi K, Barbara K, Giorge K, Vazha K, Eldar K, Otar K, David K 2017 A & A 2 20
[4] 钱鸿鹄, 孟炳寰, 袁银麟, 洪津, 张苗苗, 李双, 裘桢炜 2017 66 100701
Google Scholar
Qian H H, Meng B H, Yuan Y L, Hong J, Zhang M M, Li S, Qiu Z W 2017 Acta Phys. Sin. 66 100701
Google Scholar
[5] Huang X, Bai J, Wang K, Liu Q, Luo Y, Yang K, Zhang X 2017 Opt. Express 25 001173
Google Scholar
[6] Jacques S L, Roussel S, Samatham R 2016 J. Biomed. Opt. 21 071115
Google Scholar
[7] Azzam R M A 1982 Opt. Acta 29 685
Google Scholar
[8] Pezzaniti J L, Chenault D, Roche M, Reinhardt J, Pezzaniti J P, Schultz H 2008 Proc. SPIE 6972 69720J
Google Scholar
[9] Oka K, Kaneko T 2003 Opt. Express 11 1510
Google Scholar
[10] Luo H T, Oka K, DeHoog E, Kudenov M, Schiewgerling J, Dereniak E L 2008 Appl. Opt. 47 4413
Google Scholar
[11] Cao Q Z, Zhang C M, DeHoog E 2012 Appl. Opt. 51 5791
Google Scholar
[12] Saito N, Odate S, Otaki K, Kubota M, Kitahara R, Oka K 2013 Proc. SPIE 8873 88730M−1
Google Scholar
[13] 权乃承, 张淳民, 穆廷魁 2016 65 080703
Quan N C, Zhang C M, Mu T K 2016 Acta Phys. Sin. 65 080703
[14] Feng B, Shi Z L, Liu H Z, Liu L, Zhao Y H, Zhang J C 2018 J. Optics-UK 20 065703
Google Scholar
[15] 李翠丽, 孙晓兵, 王涵, 韦玮, 舒存铭 2014 光学学报 34 0412004
Li C L, Sun X B, Wang H, Wei W, Shu C M 2014 Acta Optica Sinica 34 0412004
[16] Liu Z, Yang W F, Ye Q H, Hong J, Gong G Y, Zheng X B 2016 Appl. Optics 55 1934
Google Scholar
[17] 李浩, 朱京平, 张宁, 张云尧, 强帆, 宗康 2016 65 134202
Google Scholar
Li H, Zhu J P, Zhang N, Zhang Y Y, Qiang F, Zong K 2016 Acta Phys. Sin. 65 134202
Google Scholar
[18] Mu T K, Zhang C M, Li Q W, Liang R G 2015 Opt. Express 23 10822
Google Scholar
[19] Alenin A S, Vaughn I J, Tyo J S 2018 Appl. Optics 57 2327
Google Scholar
[20] 黎高平, 王雷, 谢毅 2009 宇航计测技术 29 55
Google Scholar
Li G P, Wang L, Xie Y 2009 Journal of Astronautic Metrology and Measurement 29 55
Google Scholar
[21] 廖延彪 2003 偏振光学 (北京: 科学出版社)第45−63页
Liao Y B 2003 Polarization Optics (Beijing: Science Press) pp45−63 (in Chinese)
-
图 1 分振幅型全Stokes同时偏振成像系统原理图
Fig. 1. Scheme of the division-of-amplitude full Stokes simultaneous polarization imaging system.
图 2 不同入射光情况下的Stokes参数测量误差 (a) 自然光; (b) 0° 线偏光; (c) 90° 线偏光; (d) 45° 线偏光; (e) 135° 线偏光; (f) 右旋圆偏光; (g) 左旋圆偏光
Fig. 2. Errors of Stokes parameters of different incident light: (a) Unpolarized light; (b) 0° liner polarized light; (c) 90° liner polarized light; (d) 45° liner polarized light; (e) 135° liner polarized light; (f) right circularly polarized light; (g) left circularly polarized light.
图 3 邦加球球面上选取1000个不同偏振态的Stokes矢量的 (a) 三维分布和(b) Stokes参数的数值分布
Fig. 3. (a) 3D distribution and (b) stokes parameters values of 1000 Stokes vectors different degrees of polarization selected on the Poincaré sphere.
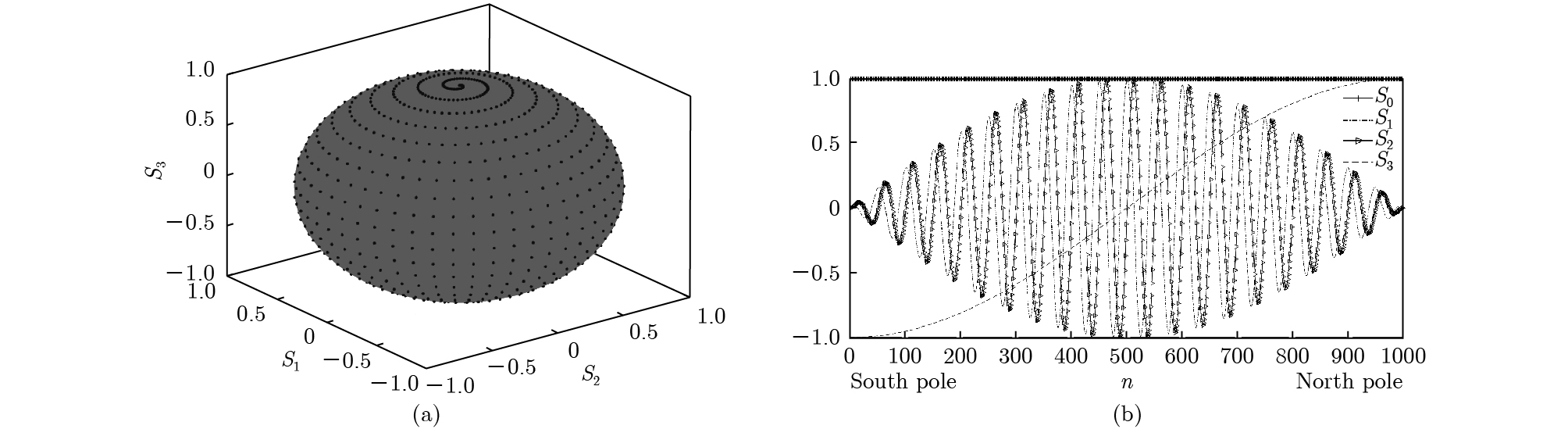
图 4 1000个邦加球球面上的入射光采样点的Stokes参数测量误差 (a) 仅存在1°的 HWP相位延迟误差; (b) 仅存在1°的QWP相位延迟误差
Fig. 4. The measurement errors of Stokes parameters of 1000 incident light sampling points selected on the Poincaré sphere is simulated: (a) There is only 1° phase delay error of HWP; (b) there is only 1° phase delay error of QWP in the system.
图 5 不同偏振度的采样点作为入射光时对偏振测量精度的影响 (a) 仅HWP相位延迟误差; (b) 仅QWP相位延迟误差; (c) HWP和QWP相位延迟耦合误差
Fig. 5. When the sampling points with different degrees of polarization are used as incident light, the effect of measurement accuracy: (a) The phase delay error of the HWP; (b) the phase delay error of the QWP; (c) the phase delay errors of the HWP and the QWP on polarization.
图 6 1000个邦加球球面上的入射光采样点的偏振度测量误差 (a) 仅存在1°的HWP相位延迟误差; (b) 仅存在1°的QWP相位延迟误差
Fig. 6. The measurement errors of DOP of 1000 incident light sampling points selected on the Poincaré sphere is simulated: (a) There is only 1° phase delay error of HWP; (b) there is only 1° phase delay error of QWP in the system.
图 7 入射光的偏振度
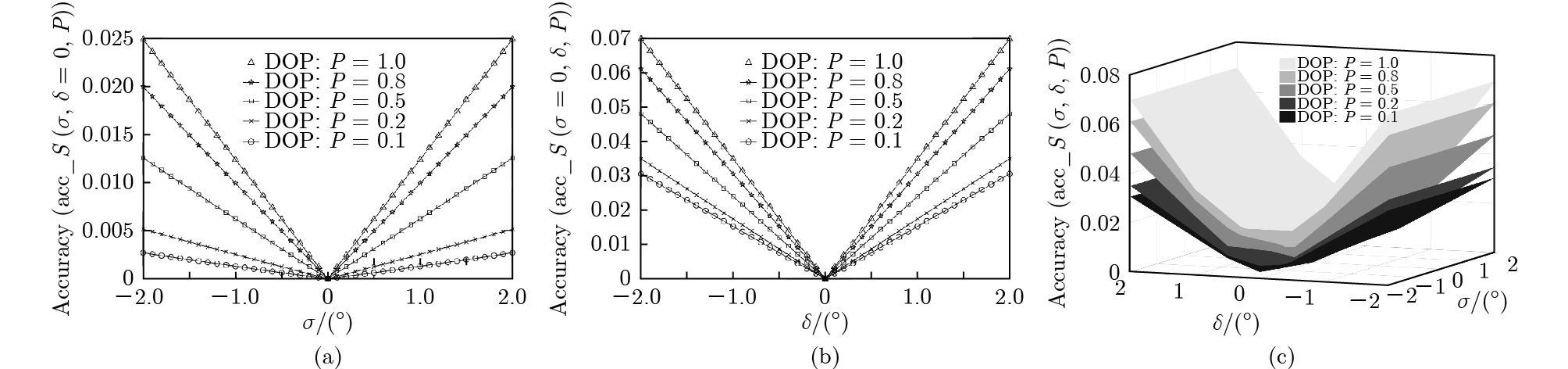
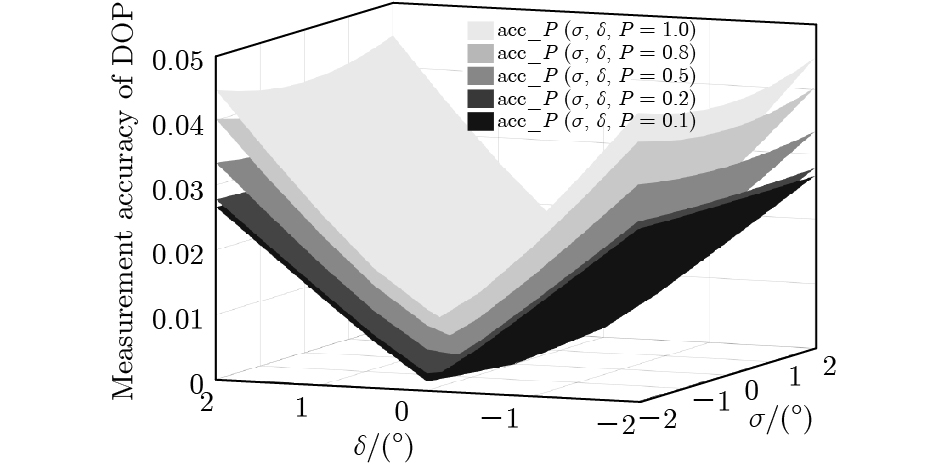
$P$ 分别为1.0, 0.8, 0.5, 0.2和0.1时, 偏振度测量精度${\rm{acc}}\_P (\sigma ,\delta ,P)$ 随HWP相位延迟误差$\sigma $ 和QWP相位延迟误差$\delta $ 的变化关系Fig. 7. Variation relation of measure accuracy
${\rm{acc}}\_P (\sigma ,\delta ,P)$ of DOP with the phase delay error of HWP and the phase delay error of QWP under the condition of$P$ = 1.0, 0.8, 0.5, 0.2 and 0.1.
图 8 波片相位延迟误差分析实验光路
Fig. 8. Experimental optical path of wave plate phase delay error analysis.
图 9 实验中HWP相位延迟误差
$\sigma$ = −0.26°和QWP相位延迟误差$\delta $ = −0.13°时的测量结果 入射光 (a)${{{S}}_0}$ 分量; (b)${{{S}}_1}$ 分量; (c)${{{S}}_2}$ 分量; (d)${{{S}}_3}$ 分量; (e) 偏振度Fig. 9. Measurement results: (a)
${{{S}}_0}$ component; (b)${{{S}}_1}$ component; (c)${{{S}}_2}$ component; (d)${{{S}}_3}$ component; (e) DOP of the incident light under the condition of$\sigma $ = −0.26° and$\delta$ = −0.13°.表 1 分振幅型全Stokes同时偏振成像系统设计参数
Table 1. Parameters of division-of-amplitude full Stokes simultaneous polarization imaging system.
参数名称 参数值 1/2波片相位延迟量
(Retardance of HWP)180° 1/4波片相位延迟量
(Retardance of QWP)90° 1/2波片快轴方位角
(Fast axis orientation of HWP)−22.5° 1/4波片快轴方位角
(Fast axis orientation of QWP)45° 部分偏振分束器分束比
(Splitting ratio of PPBS)Tp/Ts = 0.8/0.2 
下载: 导出CSV
表 2 系统偏振度测量精度
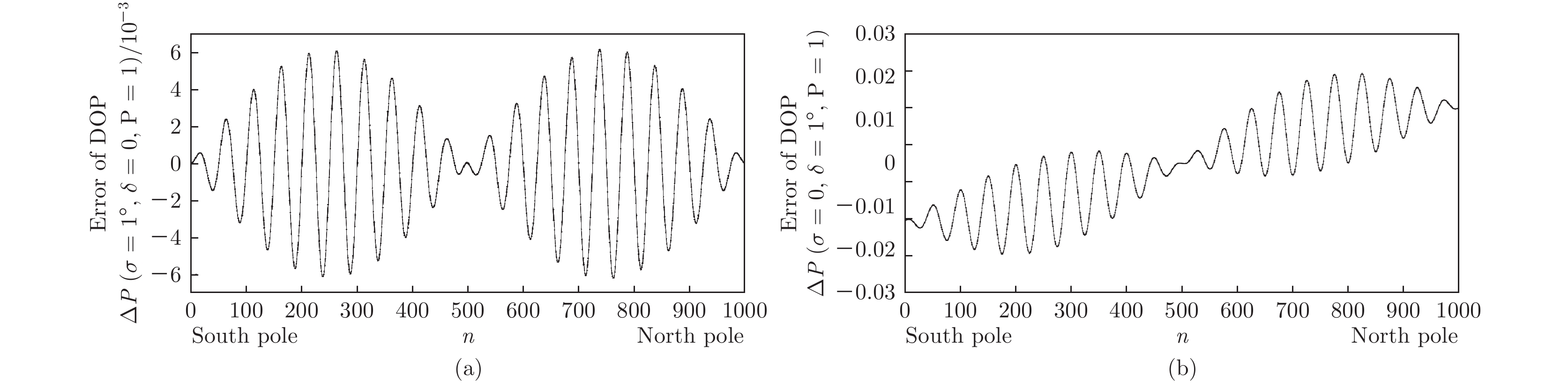
${\rm{acc}}\_P(\sigma ,\delta ,P {\rm{ = }} 1)$ 随HWP相位延迟误差$\sigma $ 和QWP相位延迟误差$\delta $ 的变化关系Table 2. Variation relation of measure accuracy
${\rm{acc}}\_P(\sigma ,\delta ,P {\rm{ = }} 1)$ of DOP with the phase delay error$\sigma $ of HWP and the phase delay error$\delta $ of QWP.$\sigma $ $\delta$ −1.0° −0.9° −0.6° −0.5° 0° 0.5° 0.6° 0.9° 1.0° −3.2° 3.22% 3.07% 2.65% 2.53% 2.03% 2.54% 2.68% 3.11% 3.26% −3.1° 3.17% 3.02% 2.59% 2.47% 1.97% 2.48% 2.62% 3.05% 3.20% −1.7° 2.50% 2.32% 1.82% 1.66% 1.06% 1.67% 1.83% 2.33% 2.50% −1.6° 2.46% 2.28% 1.77% 1.61% 1.00% 1.62% 1.78% 2.28% 2.46% −0.5° 2.13% 1.92% 1.31% 1.12% 0.31% 1.12% 1.31% 1.92% 2.13% 0° 2.09% 1.88% 1.25% 1.04% 0 1.04% 1.25% 1.88% 2.09% 0.5° 2.13% 1.92% 1.32% 1.12% 0.31% 1.12% 1.32% 1.92% 2.13% 1.6° 2.45% 2.27% 1.77% 1.62% 1.00% 1.61% 1.77% 2.27% 2.45% 1.7° 2.49% 2.31% 1.82% 1.67% 1.06% 1.66% 1.82% 2.31% 2.49% 3.1° 3.20% 3.05% 2.64% 2.50% 1.95% 2.46% 2.59% 3.02% 3.17% 3.2° 3.25% 3.11% 2.70% 2.57% 2.02% 2.52% 2.65% 3.07% 3.22%
下载: 导出CSV
表 3 系统偏振测量精度
${\rm{acc}}\_{{{S}}^{\left( {\sigma ,\delta } \right)}}$ 随HWP相位延迟误差$\sigma $ 和QWP相位延迟误差$\delta $ 的变化关系Table 3. Variation relation of system polarization measurement accuracy
${\rm{acc}}\_{{{S}}^{\left( {\sigma ,\delta } \right)}}$ with the phase delay error$\sigma $ of HWP and the phase delay error$\delta $ of QWP.$\sigma$ $\delta $ −1.0° −0.9° −0.6° −0.5° 0° 0.5° 0.6° 0.9° 1.0° −3.2° 4.01% 4.01% 4.01% 4.01% 4.01% 4.01% 4.01% 4.01% 4.01% −3.1° 3.88% 3.88% 3.88% 3.88% 3.88% 3.88% 3.88% 3.88% 3.88% −1.7° 3.48% 3.14% 2.11% 2.11% 2.11% 2.11% 2.11% 3.14% 3.48% −1.6° 3.48% 3.14% 2.09% 1.99% 1.99% 1.99% 2.09% 3.14% 3.48% −0.5° 3.48% 3.14% 2.09% 1.74% 0.62% 1.74% 2.09% 3.14% 3.48% 0° 3.48% 3.14% 2.09% 1.74% 0 1.74% 2.09% 3.14% 3.48% 0.5° 3.48% 3.14% 2.09% 1.74% 0.62% 1.74% 2.09% 3.14% 3.48% 1.6° 3.48% 3.14% 2.09% 1.99% 1.99% 1.99% 2.09% 3.14% 3.48% 1.7° 3.48% 3.14% 2.11% 2.11% 2.11% 2.11% 2.11% 3.14% 3.48% 3.1° 3.88% 3.88% 3.88% 3.88% 3.88% 3.88% 3.88% 3.88% 3.88% 3.2° 4.01% 4.01% 4.01% 4.01% 4.01% 4.01% 4.01% 4.01% 4.01%
下载: 导出CSV
表 4 实验光路中PSG的主要参数
Table 4. Parameters of PSG in the experimental optical path.
参数名称 参数值 He-Ne激光器输出波长 632.99 nm He-Ne激光器光强稳定性 ± 0.1% 电动转台旋转精度 0.005° 偏振片消光系数 ≥ 10000∶1 零级QWP相位延迟量 89.87°@632.99 nm
下载: 导出CSV
表 5 实验光路中四分束偏振分析器的主要参数
Table 5. Parameters of the four-paths polarization analyzer in the experimental optical path.
参数名称 参数值 PPBS分束比${{T_{\rm p}^{({\rm PPBS})}} / {T_{\rm s}^{({\rm PPBS})}}}$ 0.788/0.191 零级HWP相位延迟量 179.74°@632.99 nm 零级QWP相位延迟量 89.87°@632.99 nm 零级HWP快轴方位角 −22.5° 零级QWP快轴方位角 45° PBS1分束比${{T_{\rm{p}}^{({\rm{PBS1}})}} / {T_{\rm{s}}^{({\rm{PBS1}})}}}$ 0.981/0.0007 PBS2分束比${{T_{\rm{p}}^{({\rm{PBS2}})}} / {T_{\rm{s}}^{({\rm{PBS2}})}}}$ 0.988/0.0008
下载: 导出CSV
-
[1] Zhao H J, Xu W J 2016 Sensors 16 1223
Google Scholar
[2] 韩平丽, 刘飞, 张广, 陶禹, 邵晓鹏 2018 67 054202
Han P L, Liu F, Zhang G, Tao Y, Shao X P 2018 Acta Phys. Sin. 67 054202
[3] Teimuraz K, Giorgi K, Barbara K, Giorge K, Vazha K, Eldar K, Otar K, David K 2017 A & A 2 20
[4] 钱鸿鹄, 孟炳寰, 袁银麟, 洪津, 张苗苗, 李双, 裘桢炜 2017 66 100701
Google Scholar
Qian H H, Meng B H, Yuan Y L, Hong J, Zhang M M, Li S, Qiu Z W 2017 Acta Phys. Sin. 66 100701
Google Scholar
[5] Huang X, Bai J, Wang K, Liu Q, Luo Y, Yang K, Zhang X 2017 Opt. Express 25 001173
Google Scholar
[6] Jacques S L, Roussel S, Samatham R 2016 J. Biomed. Opt. 21 071115
Google Scholar
[7] Azzam R M A 1982 Opt. Acta 29 685
Google Scholar
[8] Pezzaniti J L, Chenault D, Roche M, Reinhardt J, Pezzaniti J P, Schultz H 2008 Proc. SPIE 6972 69720J
Google Scholar
[9] Oka K, Kaneko T 2003 Opt. Express 11 1510
Google Scholar
[10] Luo H T, Oka K, DeHoog E, Kudenov M, Schiewgerling J, Dereniak E L 2008 Appl. Opt. 47 4413
Google Scholar
[11] Cao Q Z, Zhang C M, DeHoog E 2012 Appl. Opt. 51 5791
Google Scholar
[12] Saito N, Odate S, Otaki K, Kubota M, Kitahara R, Oka K 2013 Proc. SPIE 8873 88730M−1
Google Scholar
[13] 权乃承, 张淳民, 穆廷魁 2016 65 080703
Quan N C, Zhang C M, Mu T K 2016 Acta Phys. Sin. 65 080703
[14] Feng B, Shi Z L, Liu H Z, Liu L, Zhao Y H, Zhang J C 2018 J. Optics-UK 20 065703
Google Scholar
[15] 李翠丽, 孙晓兵, 王涵, 韦玮, 舒存铭 2014 光学学报 34 0412004
Li C L, Sun X B, Wang H, Wei W, Shu C M 2014 Acta Optica Sinica 34 0412004
[16] Liu Z, Yang W F, Ye Q H, Hong J, Gong G Y, Zheng X B 2016 Appl. Optics 55 1934
Google Scholar
[17] 李浩, 朱京平, 张宁, 张云尧, 强帆, 宗康 2016 65 134202
Google Scholar
Li H, Zhu J P, Zhang N, Zhang Y Y, Qiang F, Zong K 2016 Acta Phys. Sin. 65 134202
Google Scholar
[18] Mu T K, Zhang C M, Li Q W, Liang R G 2015 Opt. Express 23 10822
Google Scholar
[19] Alenin A S, Vaughn I J, Tyo J S 2018 Appl. Optics 57 2327
Google Scholar
[20] 黎高平, 王雷, 谢毅 2009 宇航计测技术 29 55
Google Scholar
Li G P, Wang L, Xie Y 2009 Journal of Astronautic Metrology and Measurement 29 55
Google Scholar
[21] 廖延彪 2003 偏振光学 (北京: 科学出版社)第45−63页
Liao Y B 2003 Polarization Optics (Beijing: Science Press) pp45−63 (in Chinese)
下载:
计量
- 文章访问数: 9903
- PDF下载量: 138
- 被引次数: 0
