-
The bunching and antibunching effects of light fields reflect the spatiotemporal correlation of photons and are key indicators for distinguishing classical and non-classical quantum statistics. They play a crucial role in quantum information processing and precise measurement. In this paper, we investigate the super-bunching and antibunching effects of the full-time-delay higher-order coherence function $ {g^{(n)}} $ for squeezed thermal states and squeezed number states based on a multi-cascaded Hanbury Brown–Twiss single-photon detection scheme. Under ideal conditions, the high-order coherence of squeezed thermal states and squeezed number states is analyzed by changing compression parameter $ r $, average photon number $ \alpha $, and squeezed photon number $ n $. The results indicate that when the compression parameter $ r \in [0, 1] $, the squeezed thermal state exhibits a significant super-bunching effect, with super-bunching values of each order being $ {g^{({2})}} = 9.98 \times 10^5$, $ {g^{({3})}} = 8.98 \times 10^6$, $ {g^{({4})}} = 8.96 \times 10^{12}$, $ {g^{({5})}} = 2.24 \times 10^{14}$. The squeezed number state exhibits a continuous transition from antibunching to bunching behavior, with coherence degrees of different orders being $ {g^{({2})}} \in [1.60 \times 10^{-5}, 1.09] $, $ {g^{({3})}} \in [9.02 \times 10^{-6}, 1.16] $, $ {g^{({4})}} \in [4.75 \times 10^{-6}, 1.22] $, and $ {g^{({5})}} \in [9.39 \times 10^{-6}, 1.30]) $. Simultaneously, this study analyzes the high-order photon coherence of squeezed thermal states and squeezed number states under experimental conditions, with background noise $\gamma $ and detection efficiency $\eta $ taken into account. When detection efficiency is relatively low and background noise is substantial, the higher-order coherence of squeezed thermal states with smaller average photon number $ \alpha $ is disturbed by background noise, but still maintains good super-bunching characteristics. However, when the average photon number $ \alpha $ becomes large, which is limited by the dead time of single-photon detector, it is challenging to accurately obtain all the information about the squeezed number state light field, leading measurement results to deviate from the ideal values. When the average photon number is $ \alpha = 0.5$, the super-bunching effects reach their maximum values of $ {g^{({2})}} = 2.149 $, $ {g^{({3})}} = 6.389 $和$ {g^{({4})}} = 23.228 $, corresponding to the squeezing degrees $ {S^{({2})}} = 5.47$, $ {S^{(3)}}= 4.86 $ and = 4.43, respectively. Furthermore, by adjusting the number of squeezed photons $ n $ and the squeezing degree of the squeezed number state light field, $S$, a continuous and wide-ranging change of high-order coherence function can be achieved, transforming from anti-bunching effect to super-bunching effect. Additionally, under the conditions of high environmental noise and low detection efficiency, higher-order coherence exhibits greater sensitivity to variations in optical field parameters than lower-order coherence. Furthermore, squeezed number states with multi-photon characteristics are less susceptible to disturbances from background noise, demonstrating stronger robustness. In addition, the variation characteristics of the high-order photon coherence function of the squeezed thermal state light field under the full time-delay conditions are investigated. The full time-delay high-order coherence $ {g^{(n)}} $ of the squeezed thermal state light field near the coherence time range $ {\tau _{{\text{STS}}}} $ is significantly higher than that of the classical thermal state light field. Even when a significant time delay is introduced into one of the optical paths, partial synchronization among photons can still maintain a certain correlation strength. Although unsynchronized photons lead to an overall reduction in coherence, the coherence is still higher than the theoretical predictions for thermal states under identical conditions. Based on the theoretical framework established in this work, future experiments may focus on adjusting the pump power, intracavity loss, and crystal temperature of optical parametric amplifiers to jointly control the squeezing degree and mean photon number, enabling stable generation of squeezed thermal states in different parameter regimes. Additionally, the precise measurement of higher-order coherence can be achieved using cascaded HBT detection systems with multiple inputs and high temporal resolution. In summary, by considering environmental noise, detection efficiency, and time delay, and by adjusting the average photon number, the number of squeezed photons, and the squeezing parameters, this method can prepare super-bunching squeezed thermal states and squeezed number states, whose higher-order coherence can be continuously adjusted over a wide range, thereby facilitating efficient quantum state preparation and manipulation, as well as high-resolution quantum imaging. -
Keywords:
- high-order photon coherence /
- squeezed thermal state /
- squeezed number state /
- super-bunching effect
[1] 彭堃墀, 黄茂全, 刘晶, 廉毅敏, 张天才, 于辰, 谢常德, 郭光灿 1993 42 1079
 Google Scholar
Google Scholar
Peng K C, Huang M Q, Liu J, Lian Y M, Zhang T C, Yu C, Xie C D, Guo G C 1993 Acta Phys. Sin. 42 1079
 Google Scholar
Google Scholar
[2] Breitenbach G, Schiller S, Mlynek J 1997 Nature 387 471
 Google Scholar
Google Scholar
[3] 李庆回, 姚文秀, 李番, 田龙, 王雅君, 郑耀辉 2021 70 154203
 Google Scholar
Google Scholar
Li Q H, Yao W X, Li F, Tian L, Wang Y J, Zheng Y H 2021 Acta Phys. Sin. 70 154203
 Google Scholar
Google Scholar
[4] Bachor H, Ralph T C 2004 A Guide to Experiments in Quantum Optics (Berlin: Wiley) p232
[5] Slusher R E, Hollberg L W, Yurke B, Mertz J C, Valley J F 1985 Phys. Rev. Lett. 55 2409
 Google Scholar
Google Scholar
[6] Wu L A, Kimble H J, Hall J L, Wu H 1986 Phys. Rev. Lett. 57 2520
 Google Scholar
Google Scholar
[7] Vollmer C E, Baune C, Samblowski A, Eberle T, Händchen V, Fiurášek J, Schnabel R 2014 Phys. Rev. Lett. 112 73602
 Google Scholar
Google Scholar
[8] Kala V, Kopylov D, Marek P, Sharapova P 2025 Opt. Express 33 14000
 Google Scholar
Google Scholar
[9] Dorfman K, Liu S S, Lou Y B, Wei T X, Jing J T, Schlawin F, Mukamel S 2021 Proc. Natl. Acad. Sci. 118 e2105601118
 Google Scholar
Google Scholar
[10] Chembo Y K 2016 Phys. Rev. A 93 33820
 Google Scholar
Google Scholar
[11] Kim S, Marino A M 2018 Opt. Express 26 33366
 Google Scholar
Google Scholar
[12] Silverstone J W, Bonneau D, Ohira K, Suzuki N, Yoshida H, Iizuka N, Ezaki M, Natarajan C M, Tanner M G, Hadfield R H 2014 Nat. Photonics 8 104
 Google Scholar
Google Scholar
[13] Arrazola J M, Bergholm V, Brádler K, Bromley T R, Collins M J, Dhand I, Fumagalli A, Gerrits T, Goussev A, Helt L G 2021 Nature 591 54
 Google Scholar
Google Scholar
[14] Lu X, Li Q, Westly D A, Moille G, Singh A, Anant V, Srinivasan K 2019 Nat. Phys. 15 373
 Google Scholar
Google Scholar
[15] Porto C, Rusca D, Cialdi S, Crespi A, Osellame R, Tamascelli D, Olivares S, Paris M G 2018 J. Opt. Soc. Am. B 35 1596
 Google Scholar
Google Scholar
[16] Braunstein S L, Crouch D D 1991 Phys. Rev. A 43 330
 Google Scholar
Google Scholar
[17] Fanizza M, Rosati M, Skotiniotis M, Calsamiglia J, Giovannetti V 2021 Quantum 5 608
 Google Scholar
Google Scholar
[18] Deng X W, Hao S H, Tian C X, Su X L, Xie C D, Peng K C 2016 Appl. Phys. Lett. 108 081105
 Google Scholar
Google Scholar
[19] Yuen H P 2004 Quantum Squeezing (Vol. 27) (Berlin, Heidelberg: Springer Berlin Heidelberg) p227
[20] Lin S Q, Li W, Chen Z W, Shen J W, Ge B H, Pei Y Z 2016 Nat. Commun. 7 10287
 Google Scholar
Google Scholar
[21] Lawrie B J, Lett P D, Marino A M, Pooser R C 2019 ACS Photonics 6 1307
 Google Scholar
Google Scholar
[22] Yang W H, Diao W T, Cai C X, Wu T, Wu K, Li Y, Li C, Duan C D, Leng H Y, Zi N K 2022 Chemosensors 11 18
 Google Scholar
Google Scholar
[23] Zander J 2021 PhD Dissertation (Hamburg: Staats-und Universitätsbibliothek Hamburg Carl von Ossietzky
[24] Zhang Y, Menotti M, Tan K, Vaidya V D, Mahler D H, Helt L G, Zatti L, Liscidini M, Morrison B, Vernon Z 2021 Nat. Commun. 12 2233
 Google Scholar
Google Scholar
[25] Weedbrook C, Pirandola S, García-Patrón R, Cerf N J, Ralph T C, Shapiro J H, Lloyd S 2012 Rev. Mod. Phys. 84 621
 Google Scholar
Google Scholar
[26] Dupays L, Chenu A 2021 Quantum 5 449
 Google Scholar
Google Scholar
[27] Kim M S, de Oliveira F A M, Knight P L 1989 Phys. Rev. A 40 2494
 Google Scholar
Google Scholar
[28] Marian P, Marian T A 1993 Phys. Rev. A 47 4474
 Google Scholar
Google Scholar
[29] Rashid M, Tufarelli T, Bateman J, Vovrosh J, Hempston D, Kim M S, Ulbricht H 2016 Phys. Rev. Lett. 117 273601
 Google Scholar
Google Scholar
[30] Albano L, Mundarain D F, Stephany J 2002 J. Opt. B: Quantum Semiclassical Opt. 4 352
 Google Scholar
Google Scholar
[31] Marian P 1991 Phys. Rev. A 44 3325
 Google Scholar
Google Scholar
[32] Liu R F, Fang A P, Zhou Y, Zhang P, Gao S Y, Li H R, Gao H, Li F L 2016 Phys. Rev. A 93 13822
 Google Scholar
Google Scholar
[33] Tan Q S, Liao J Q, Wang X, Nori F 2014 Phys. Rev. A 89 53822
 Google Scholar
Google Scholar
[34] Guo Y Q, Peng C S, Ji Y L, Li P, Guo Y Y, Guo X M 2018 Opt. Express 26 5991
 Google Scholar
Google Scholar
[35] Guo Y Q, Zhang H J, Guo X M, Zhang Y C, Zhang T C 2022 Opt. Express 30 8461
 Google Scholar
Google Scholar
[36] Guo Y Q, Li G, Zhang Y F, Zhang P F, Wang J M, Zhang T C 2012 Sci. China Phys. , Mech. Astron. 55 1523
 Google Scholar
Google Scholar
[37] Brown R H, Twiss R Q 1956 Nature 177 27
 Google Scholar
Google Scholar
[38] 郭龑强, 王李静, 王宇, 房鑫, 赵彤, 郭晓敏 2020 69 174204
 Google Scholar
Google Scholar
Guo Y Q, Wang L J, Wang Y, Fang X, Zhao T, Guo X M Acta Phys. Sin. 2020 69 174204
 Google Scholar
Google Scholar
[39] Liu Q, Luo K H, Chen X H, Wu L A 2010 Chin. Phys. B 19 94211
 Google Scholar
Google Scholar
[40] Liu Y C, Kuang L M 2011 Phys. Rev. A 83 53808
 Google Scholar
Google Scholar
[41] Scully M O, Zubairy M S 1997 Quantum Optics (Cambridge: Cambridge University Press
[42] 张浩杰, 郭龑强, 郭晓敏, 张健飞, 左冠华, 张玉驰, 张天才 2022 71 194202
 Google Scholar
Google Scholar
Zhang H J, Guo Y Q, Guo X M, Zhang J F, Zuo G H, Zhang Y C, Zhang T C 2022 Acta Phys. Sin. 71 194202
 Google Scholar
Google Scholar
[43] Yu J, Qin Y, Qin J L, Wang H, Yan Z H, Jia X J, Peng K C 2020 Phys. Rev. Appl. 13 24037
 Google Scholar
Google Scholar
[44] Vignat C 2012 Stat. Probab. Lett. 82 67
 Google Scholar
Google Scholar
-
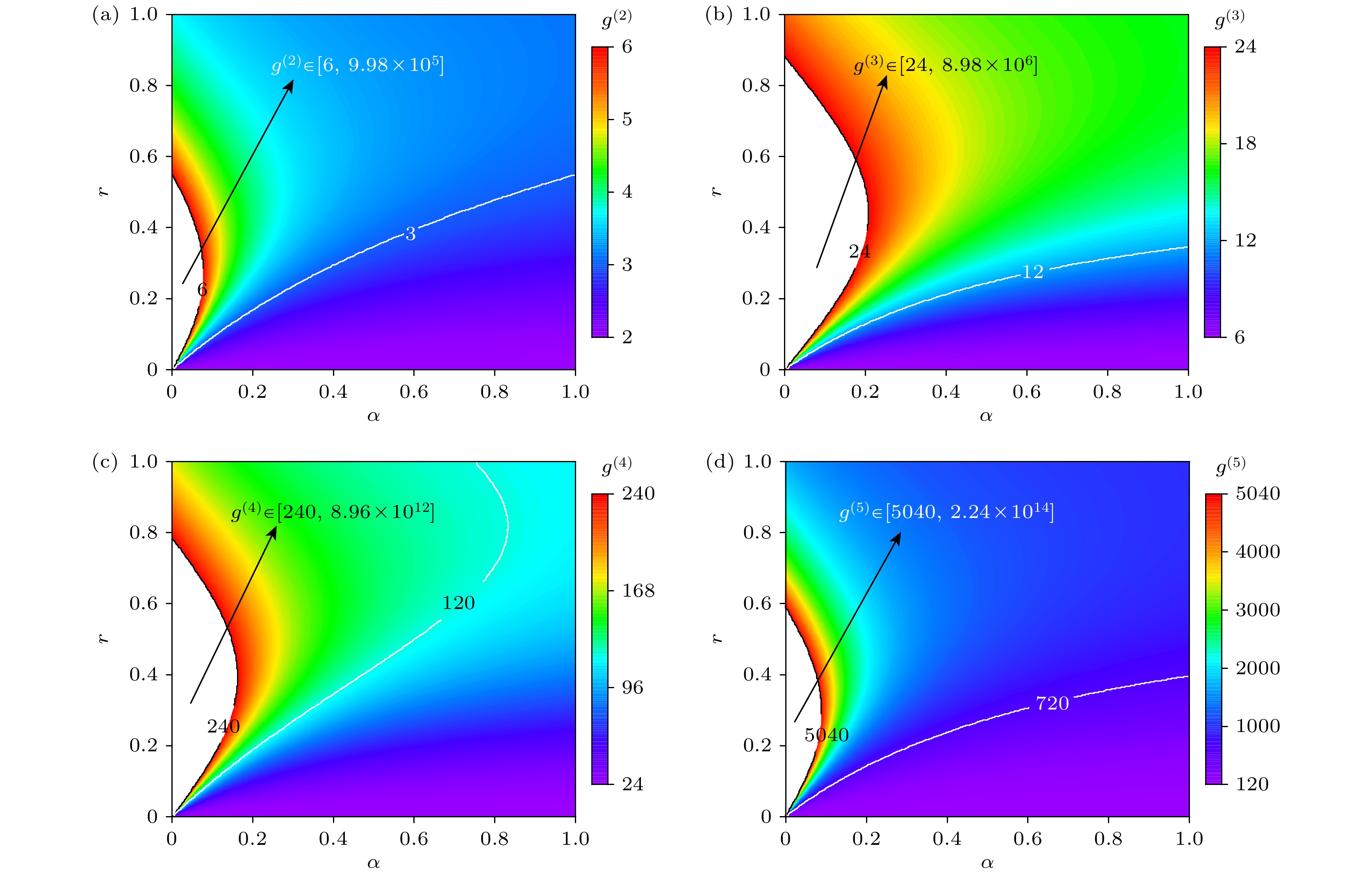
图 2 相位无关压缩热态高阶相干函数$ {g^{(n)}} $随光场平均光子数$ \alpha $和压缩参数$ r $变化的超聚束结果 (a) $ {g^{(2)}} $; (b) $ {g^{(3)}} $; (c) $ {g^{(4)}} $; (d) $ {g^{(5)}} $
Figure 2. Super-bunching results of higher-order coherence function $ {g^{(n)}} $in phase-independent squeezed thermal state varying with mean photon number $ \alpha $and squeezing parameter $ r $: (a) $ {g^{(2)}} $; (b) $ {g^{(3)}} $; (c) $ {g^{(4)}} $; (d) $ {g^{(5)}} $.
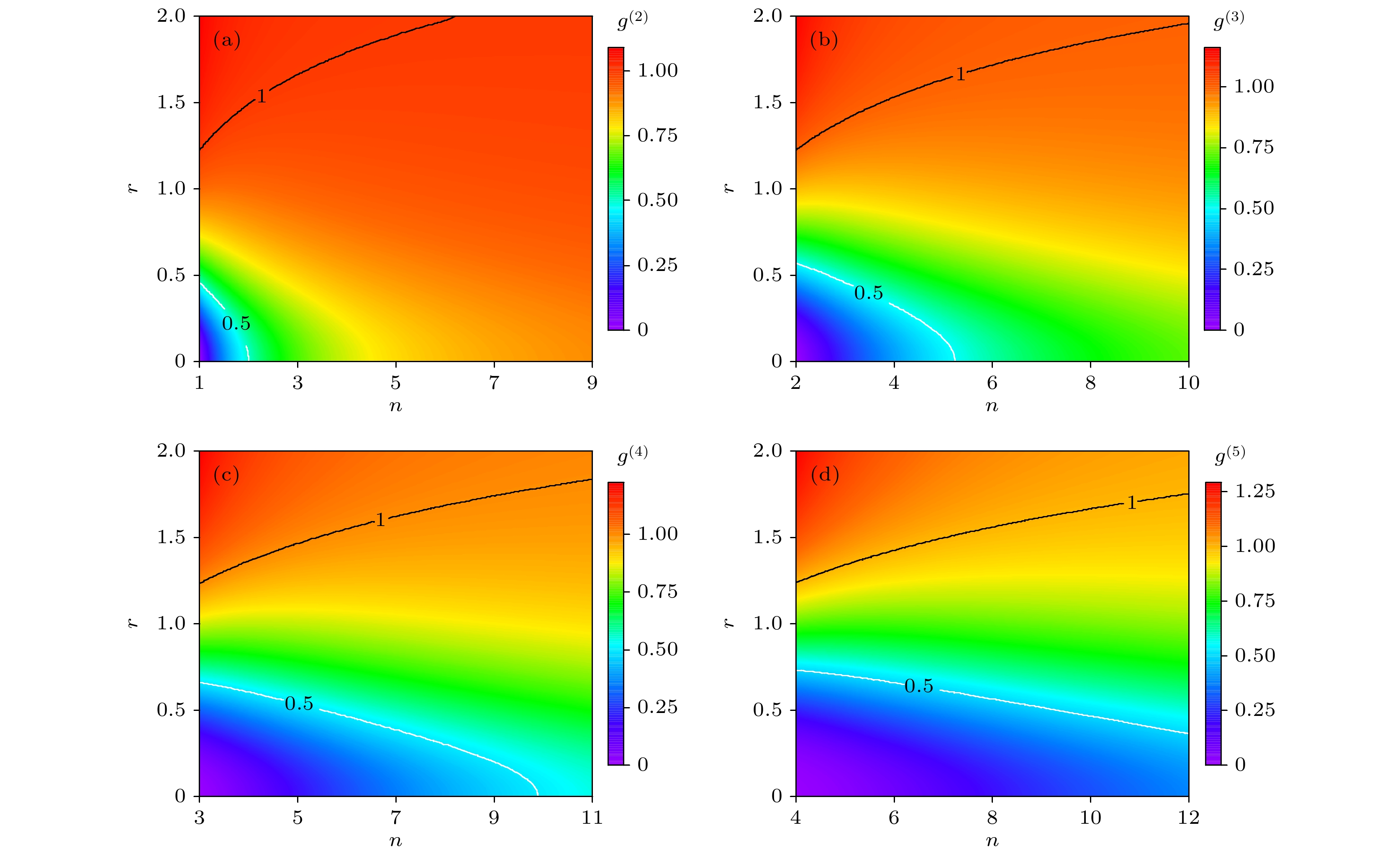
图 3 相位无关压缩数态高阶相干函数$ {g^{(n)}} $随压缩光子数$ n $和压缩参数$ r $变化的结果 (a) $ {g^{(2)}} $; (b) $ {g^{(3)}} $; (c) $ {g^{(4)}} $; (d) $ {g^{(5)}} $
Figure 3. Higher-order coherence function $ {g^{(n)}} $of phase-independent squeezed number state varying with photon number $ n $ before squeezing and squeezing parameter $ r $: (a) $ {g^{(2)}} $; (b) $ {g^{(3)}} $; (c) $ {g^{(4)}} $; (d) $ {g^{(5)}} $.
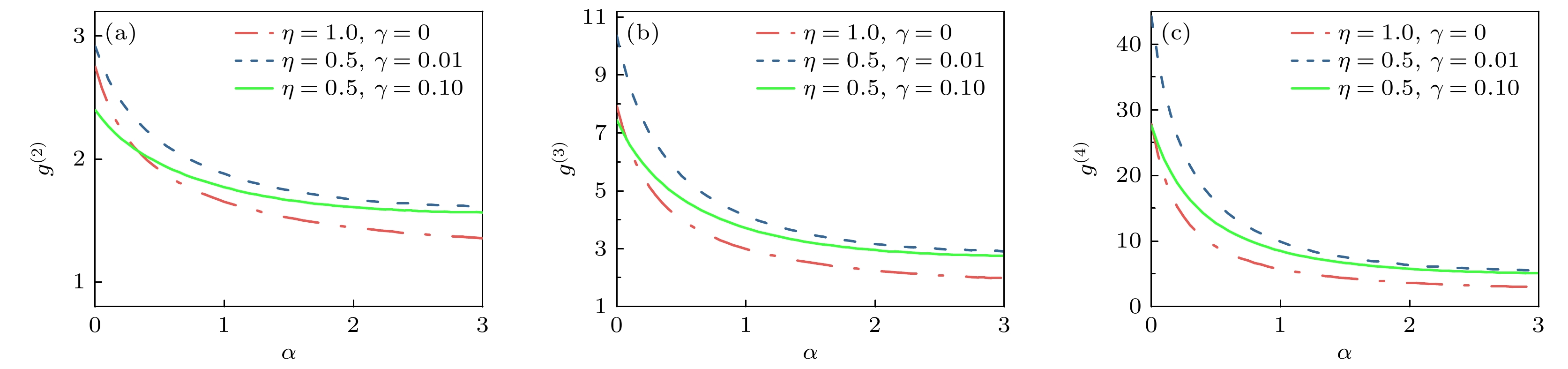
图 4 压缩参数$ r $ = 1, 探测效率与背景噪声分别为($\eta $ = 1, $\gamma $ = 0), ($\eta $ = 0.5, $\gamma $ = 0.01)和($\eta $ = 0.5, $\gamma $ = 0.1)的情况下, 压缩热态光场高阶相干函数$ {g^{(n)}} $随平均光子数$ \alpha $的变化结果 (a) $ {g^{(2)}} $; (b) $ {g^{(3)}} $; (c) $ {g^{(4)}} $
Figure 4. Higher-order coherence function $ {g^{(n)}} $of squeezed thermal state varying with mean photon number $ \alpha $ when squeezing parameter $ r $ = 1, under detection efficiency and background noise conditions of ($\eta $ = 1, $\gamma $ = 0), ($\eta $ = 0.5, $\gamma $ = 0.01), and ($\eta $ = 0.5, $\gamma $ = 0.1): (a) $ {g^{(2)}} $; (b) $ {g^{(3)}} $; (c) $ {g^{(4)}} $.
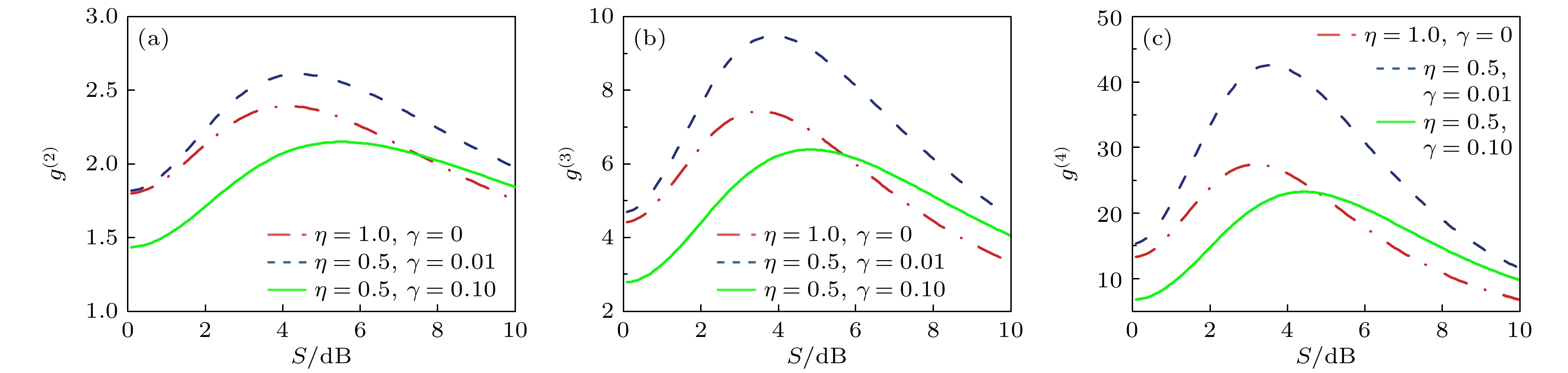
图 5 平均光子数$ \alpha $ = 0.5, 探测效率与背景噪声分别为($\eta $ = 1, $\gamma $ = 0), ($\eta $ = 0.5, $\gamma $ = 0.01)和($\eta $ = 0.5, $\gamma $ = 0.1)的情况下, 压缩热态光场高阶相干函数$ {g^{(n)}} $随压缩度$S$的变化结果 (a) $ {g^{(2)}} $; (b) $ {g^{(3)}} $; (c) $ {g^{(4)}} $
Figure 5. Higher-order coherence function $ {g^{(n)}} $of squeezed thermal state varying with squeezing degree $S$when mean photon number $ \alpha $ = 0.5, under detection efficiency and background noise conditions of ($\eta $ = 1, $\gamma $ = 0), ($\eta $ = 0.5, $\gamma $ = 0.01), and ($\eta $ = 0.5, $\gamma $ = 0.1): (a) $ {g^{(2)}} $; (b) $ {g^{(3)}} $; (c) $ {g^{(4)}} $.
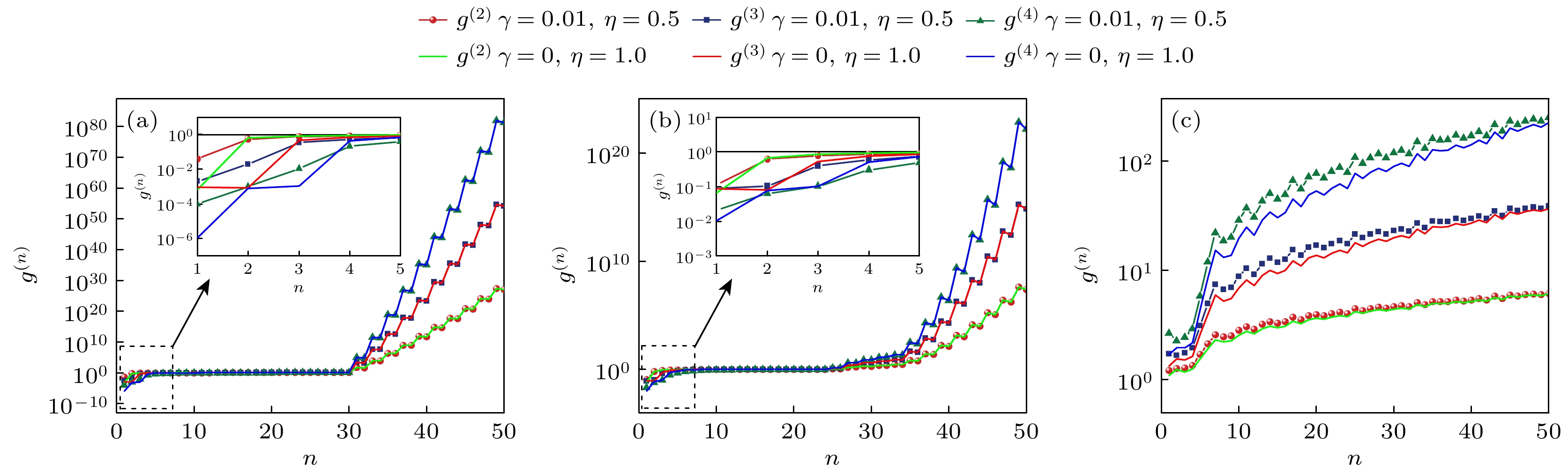
图 6 实验条件下($\eta $= 0.5, $\gamma $= 0.01)和理想条件下($\eta $= 1, $\gamma $= 0), 压缩参数 (a) $ r $= 0.01, (b) $ r $= 0.1和(c) $ r $= 1时, 压缩数态高阶相干函数$ {g^{(n)}} $随压缩前数态光子数$ n $变化的结果
Figure 6. Higher-order coherence function $ {g^{(n)}} $of squeezed number state varying with photon number $ n $without squeezing under experimental conditions ($\eta $= 0.5, $\gamma $= 0.01) and ideal conditions ($\eta $= 1, $\gamma $= 0), with squeezing parameter (a) $ r $= 0.01, (b) $ r $= 0.1, and (c) $ r $= 1.
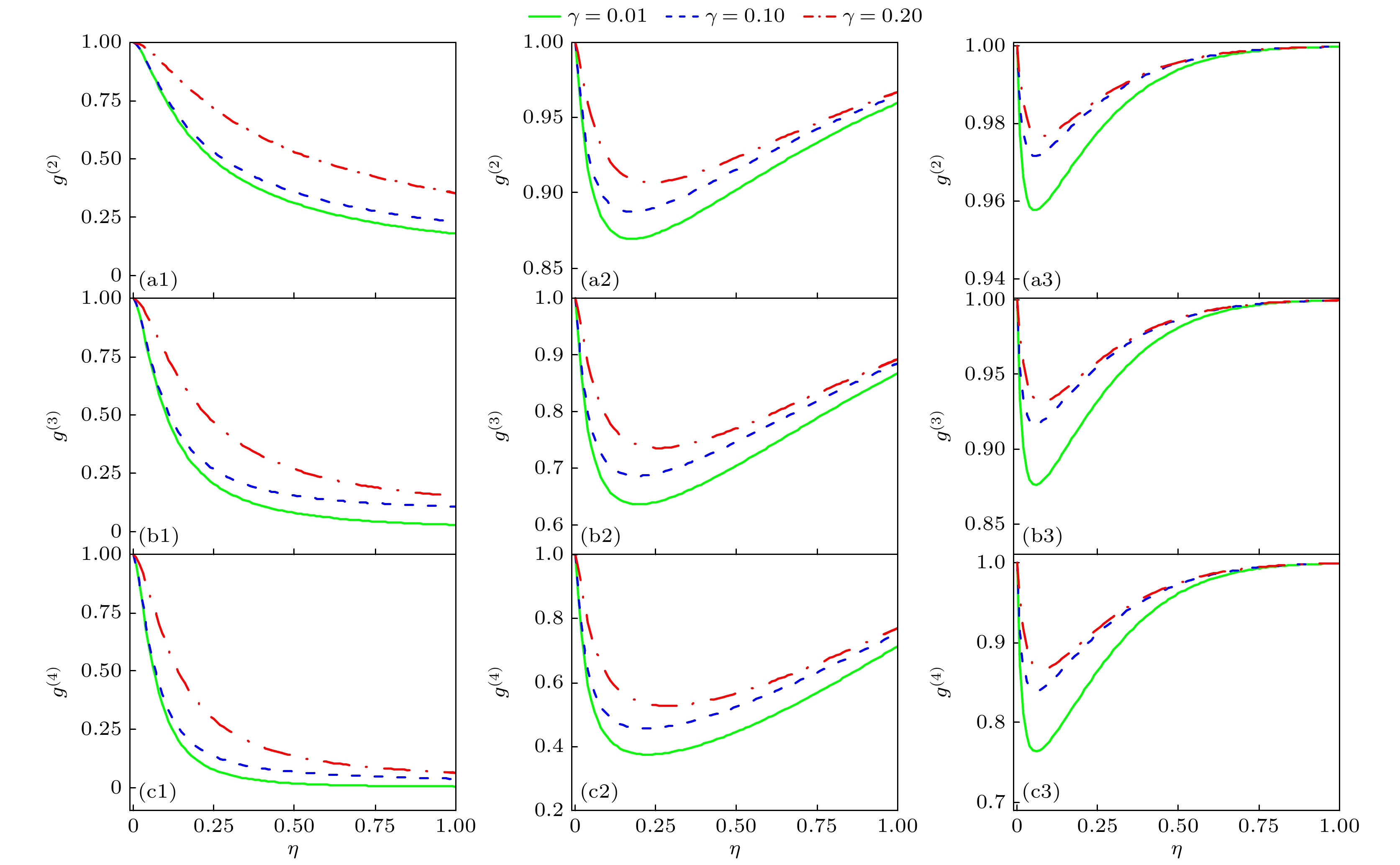
图 7 压缩参数$ r $= 0.1, 压缩光子数分别为 (a1)—(c1) $ n $ = 1, (a2)—(c2) $ n $= 5和(a3)—(c3) $ n $ = 15时, 压缩数态在不同背景噪声$\gamma $ = 0.01, 0.1, 0.2的情况下的高阶相干函数$ {g^{(n)}} $随探测效率$\eta $的变化结果
Figure 7. Higher-order coherence function $ {g^{(n)}} $of squeezed number state varying with detection efficiency $\eta $at squeezing parameter $ r $ = 0.1, with squeezed photon number (a1)–(c1) $ n $ = 1, (a2)–(c2) $ n $ = 5, and (a3)–(c3) $ n $ = 15, under different background noises $\gamma $ = 0.01, 0.1, 0.2.
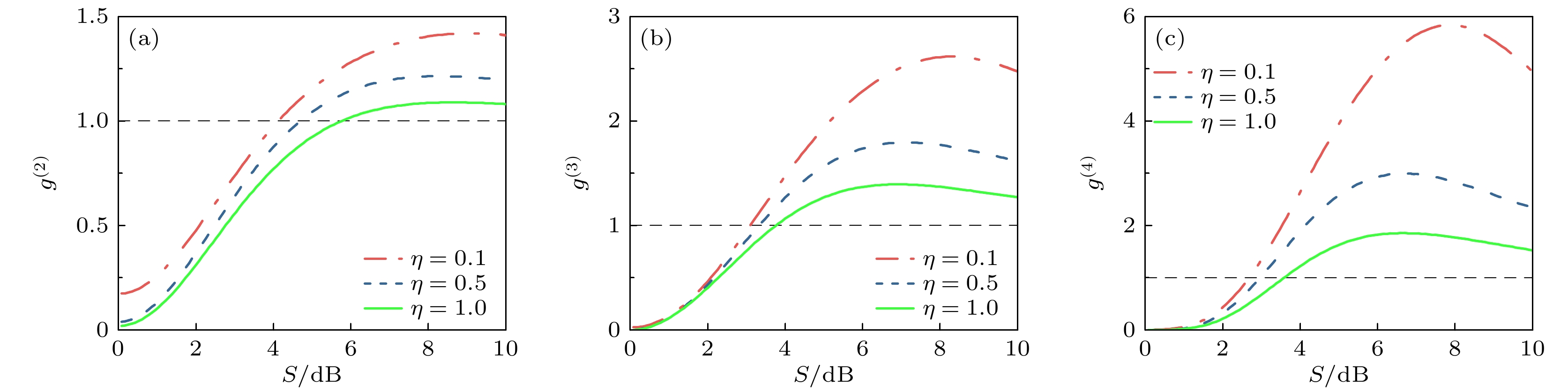
图 8 背景噪声$\gamma $ = 0.01, 压缩光子数$ n $ = 1时, 压缩数态在不同探测效率$\eta $ = 0.1, 0.5, 1情况下的高阶相干函数$ {g^{(n)}} $随压缩度$S$的变化结果 (a) $ {g^{(2)}} $; (b) $ {g^{(3)}} $; (c) $ {g^{(4)}} $
Figure 8. Higher-order coherence function $ {g^{(n)}} $of squeezed number state varying with squeezing degree $S$at background noise $\gamma $ = 0.01 and squeezed photon number $ n $ = 1, under different detection efficiencies $\eta $ = 0.1, 0.5, 1: (a) $ {g^{(2)}} $; (b) $ {g^{(3)}} $; (c) $ {g^{(4)}} $.
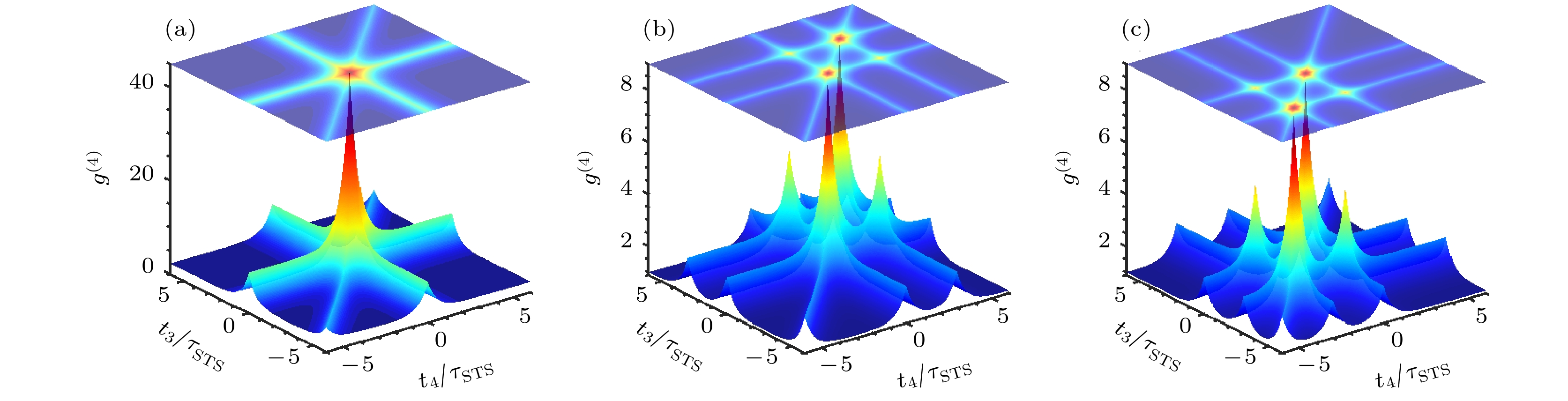
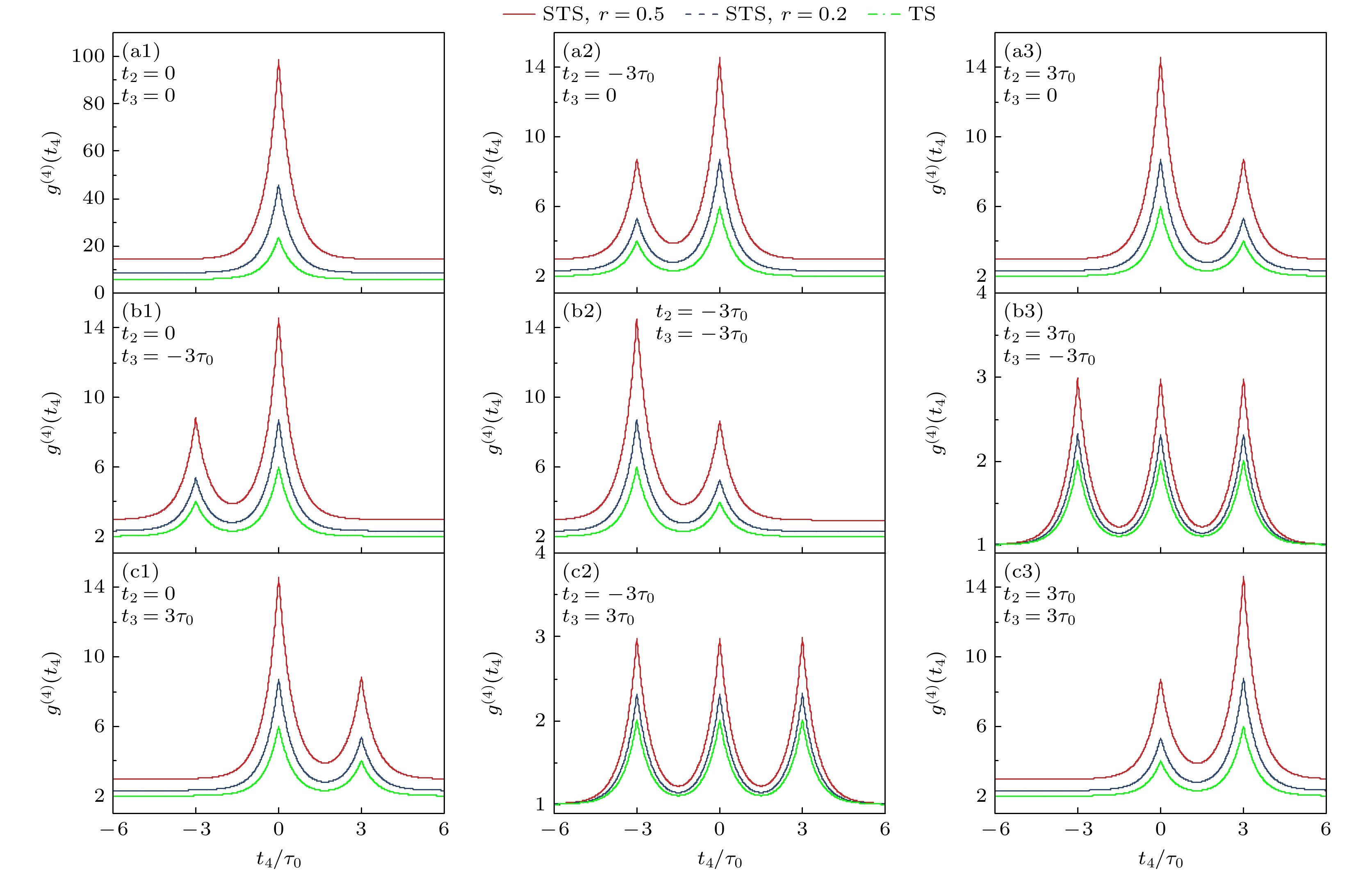
图 9 平均光子数$ \alpha $ = 1, 压缩参数$ r $ = 0.2, 压缩热态光场全时延条件下的四阶相干性$ {g^{(4)}} $随延迟时间$ {t_3} $, $ {t_4} $的变化结果 (a) $ {t_1} $ = $ 0{\tau _{{\text{STS}}}} $; $ {t_2} $ = $ 0{\tau _{{\text{STS}}}} $; (b) $ {t_1} $ = $ 0{\tau _{{\text{STS}}}} $; $ {t_2} $ = $ 3{\tau _{{\text{STS}}}} $; (c) $ {t_1} $ = $ 0{\tau _{{\text{STS}}}} $; $ {t_2} $ = $ - 3{\tau _{{\text{STS}}}} $
Figure 9. Fourth-order degree of coherence $ {g^{(4)}} $of squeezed thermal state varying with delay times $ {t_3} $, $ {t_4} $under full-delay conditions at mean photon number $ \alpha $ = 1 and squeezing parameter $ r $ = 0.2: (a) $ {t_1} $ = $ 0{\tau _{{\text{STS}}}} $;$ {t_2} $ = $ 0{\tau _{{\text{STS}}}} $; (b) $ {t_1} $ = $ 0{\tau _{{\text{STS}}}} $;$ {t_2} $ = $ 3{\tau _{{\text{STS}}}} $; (c) $ {t_1} $ = $ 0{\tau _{{\text{STS}}}} $; $ {t_2} $ = $ - 3{\tau _{{\text{STS}}}} $.
-
[1] 彭堃墀, 黄茂全, 刘晶, 廉毅敏, 张天才, 于辰, 谢常德, 郭光灿 1993 42 1079
 Google Scholar
Google Scholar
Peng K C, Huang M Q, Liu J, Lian Y M, Zhang T C, Yu C, Xie C D, Guo G C 1993 Acta Phys. Sin. 42 1079
 Google Scholar
Google Scholar
[2] Breitenbach G, Schiller S, Mlynek J 1997 Nature 387 471
 Google Scholar
Google Scholar
[3] 李庆回, 姚文秀, 李番, 田龙, 王雅君, 郑耀辉 2021 70 154203
 Google Scholar
Google Scholar
Li Q H, Yao W X, Li F, Tian L, Wang Y J, Zheng Y H 2021 Acta Phys. Sin. 70 154203
 Google Scholar
Google Scholar
[4] Bachor H, Ralph T C 2004 A Guide to Experiments in Quantum Optics (Berlin: Wiley) p232
[5] Slusher R E, Hollberg L W, Yurke B, Mertz J C, Valley J F 1985 Phys. Rev. Lett. 55 2409
 Google Scholar
Google Scholar
[6] Wu L A, Kimble H J, Hall J L, Wu H 1986 Phys. Rev. Lett. 57 2520
 Google Scholar
Google Scholar
[7] Vollmer C E, Baune C, Samblowski A, Eberle T, Händchen V, Fiurášek J, Schnabel R 2014 Phys. Rev. Lett. 112 73602
 Google Scholar
Google Scholar
[8] Kala V, Kopylov D, Marek P, Sharapova P 2025 Opt. Express 33 14000
 Google Scholar
Google Scholar
[9] Dorfman K, Liu S S, Lou Y B, Wei T X, Jing J T, Schlawin F, Mukamel S 2021 Proc. Natl. Acad. Sci. 118 e2105601118
 Google Scholar
Google Scholar
[10] Chembo Y K 2016 Phys. Rev. A 93 33820
 Google Scholar
Google Scholar
[11] Kim S, Marino A M 2018 Opt. Express 26 33366
 Google Scholar
Google Scholar
[12] Silverstone J W, Bonneau D, Ohira K, Suzuki N, Yoshida H, Iizuka N, Ezaki M, Natarajan C M, Tanner M G, Hadfield R H 2014 Nat. Photonics 8 104
 Google Scholar
Google Scholar
[13] Arrazola J M, Bergholm V, Brádler K, Bromley T R, Collins M J, Dhand I, Fumagalli A, Gerrits T, Goussev A, Helt L G 2021 Nature 591 54
 Google Scholar
Google Scholar
[14] Lu X, Li Q, Westly D A, Moille G, Singh A, Anant V, Srinivasan K 2019 Nat. Phys. 15 373
 Google Scholar
Google Scholar
[15] Porto C, Rusca D, Cialdi S, Crespi A, Osellame R, Tamascelli D, Olivares S, Paris M G 2018 J. Opt. Soc. Am. B 35 1596
 Google Scholar
Google Scholar
[16] Braunstein S L, Crouch D D 1991 Phys. Rev. A 43 330
 Google Scholar
Google Scholar
[17] Fanizza M, Rosati M, Skotiniotis M, Calsamiglia J, Giovannetti V 2021 Quantum 5 608
 Google Scholar
Google Scholar
[18] Deng X W, Hao S H, Tian C X, Su X L, Xie C D, Peng K C 2016 Appl. Phys. Lett. 108 081105
 Google Scholar
Google Scholar
[19] Yuen H P 2004 Quantum Squeezing (Vol. 27) (Berlin, Heidelberg: Springer Berlin Heidelberg) p227
[20] Lin S Q, Li W, Chen Z W, Shen J W, Ge B H, Pei Y Z 2016 Nat. Commun. 7 10287
 Google Scholar
Google Scholar
[21] Lawrie B J, Lett P D, Marino A M, Pooser R C 2019 ACS Photonics 6 1307
 Google Scholar
Google Scholar
[22] Yang W H, Diao W T, Cai C X, Wu T, Wu K, Li Y, Li C, Duan C D, Leng H Y, Zi N K 2022 Chemosensors 11 18
 Google Scholar
Google Scholar
[23] Zander J 2021 PhD Dissertation (Hamburg: Staats-und Universitätsbibliothek Hamburg Carl von Ossietzky
[24] Zhang Y, Menotti M, Tan K, Vaidya V D, Mahler D H, Helt L G, Zatti L, Liscidini M, Morrison B, Vernon Z 2021 Nat. Commun. 12 2233
 Google Scholar
Google Scholar
[25] Weedbrook C, Pirandola S, García-Patrón R, Cerf N J, Ralph T C, Shapiro J H, Lloyd S 2012 Rev. Mod. Phys. 84 621
 Google Scholar
Google Scholar
[26] Dupays L, Chenu A 2021 Quantum 5 449
 Google Scholar
Google Scholar
[27] Kim M S, de Oliveira F A M, Knight P L 1989 Phys. Rev. A 40 2494
 Google Scholar
Google Scholar
[28] Marian P, Marian T A 1993 Phys. Rev. A 47 4474
 Google Scholar
Google Scholar
[29] Rashid M, Tufarelli T, Bateman J, Vovrosh J, Hempston D, Kim M S, Ulbricht H 2016 Phys. Rev. Lett. 117 273601
 Google Scholar
Google Scholar
[30] Albano L, Mundarain D F, Stephany J 2002 J. Opt. B: Quantum Semiclassical Opt. 4 352
 Google Scholar
Google Scholar
[31] Marian P 1991 Phys. Rev. A 44 3325
 Google Scholar
Google Scholar
[32] Liu R F, Fang A P, Zhou Y, Zhang P, Gao S Y, Li H R, Gao H, Li F L 2016 Phys. Rev. A 93 13822
 Google Scholar
Google Scholar
[33] Tan Q S, Liao J Q, Wang X, Nori F 2014 Phys. Rev. A 89 53822
 Google Scholar
Google Scholar
[34] Guo Y Q, Peng C S, Ji Y L, Li P, Guo Y Y, Guo X M 2018 Opt. Express 26 5991
 Google Scholar
Google Scholar
[35] Guo Y Q, Zhang H J, Guo X M, Zhang Y C, Zhang T C 2022 Opt. Express 30 8461
 Google Scholar
Google Scholar
[36] Guo Y Q, Li G, Zhang Y F, Zhang P F, Wang J M, Zhang T C 2012 Sci. China Phys. , Mech. Astron. 55 1523
 Google Scholar
Google Scholar
[37] Brown R H, Twiss R Q 1956 Nature 177 27
 Google Scholar
Google Scholar
[38] 郭龑强, 王李静, 王宇, 房鑫, 赵彤, 郭晓敏 2020 69 174204
 Google Scholar
Google Scholar
Guo Y Q, Wang L J, Wang Y, Fang X, Zhao T, Guo X M Acta Phys. Sin. 2020 69 174204
 Google Scholar
Google Scholar
[39] Liu Q, Luo K H, Chen X H, Wu L A 2010 Chin. Phys. B 19 94211
 Google Scholar
Google Scholar
[40] Liu Y C, Kuang L M 2011 Phys. Rev. A 83 53808
 Google Scholar
Google Scholar
[41] Scully M O, Zubairy M S 1997 Quantum Optics (Cambridge: Cambridge University Press
[42] 张浩杰, 郭龑强, 郭晓敏, 张健飞, 左冠华, 张玉驰, 张天才 2022 71 194202
 Google Scholar
Google Scholar
Zhang H J, Guo Y Q, Guo X M, Zhang J F, Zuo G H, Zhang Y C, Zhang T C 2022 Acta Phys. Sin. 71 194202
 Google Scholar
Google Scholar
[43] Yu J, Qin Y, Qin J L, Wang H, Yan Z H, Jia X J, Peng K C 2020 Phys. Rev. Appl. 13 24037
 Google Scholar
Google Scholar
[44] Vignat C 2012 Stat. Probab. Lett. 82 67
 Google Scholar
Google Scholar
Catalog
Metrics
- Abstract views: 750
- PDF Downloads: 38
- Cited By: 0














 DownLoad:
DownLoad: