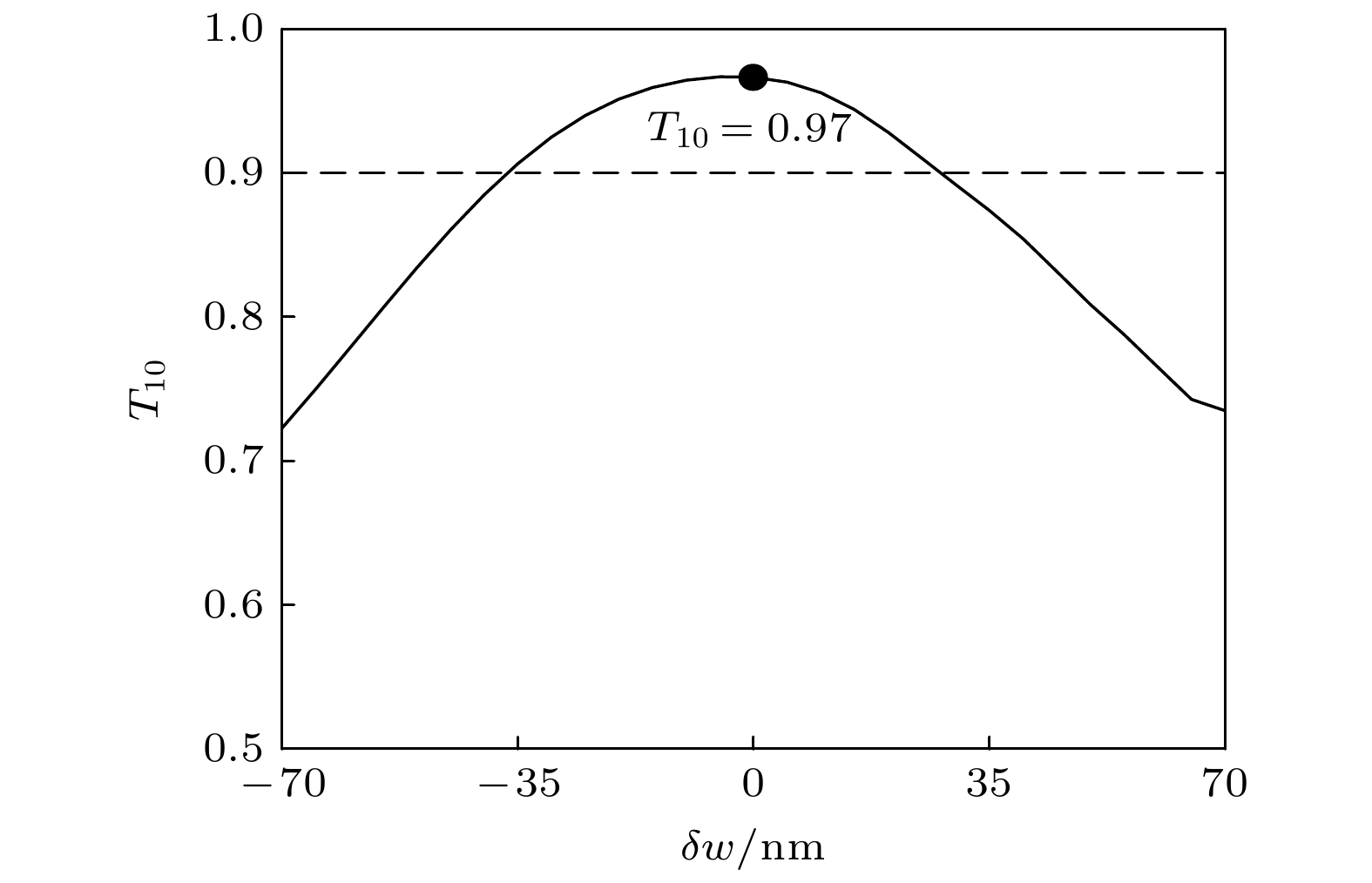
-
Topological pumping based on Thouless pumping can be effectively applied to optical waveguide array systems to achieve robust light manipulation with strong disturbance resistance. One of its typical models, the Rice-Mele (R-M) model, enables directional light field to transmit from the leftmost (rightmost) waveguide to the rightmost (leftmost) waveguide, which can be utilized to realize fabrication-tolerant optical couplers. Adiabatic evolution is a critical factor influencing the transport of topological eigenstates. However, it requires the system’s parameter variation to be sufficiently slow, which leads to excessively long waveguide lengths, limiting device compactness. To reduce the size, non-adiabatic evolution offers a feasible alternative. Meanwhile, the adiabatic properties of topological pumping models introduce new degrees of freedom, expanding possibilities for light manipulation. Based on the R-M model, this work analyzes the relationship between adiabatic property and structure length L, investigates light field evolution behavior when adiabatic condition is violated, and explores the transition from adiabatic to non-adiabatic regimes. When adiabatic condition is satisfied (L1 = 1000 μm), the light field evolution aligns with the eigen edge state. The output mode is manifested as an edge state and localized at the edge waveguide. As length shortens (L2 = 250 μm and L4 = 30 μm), the deviation between light field and eigen edge state arises, and the eigen bulk states get involved in the light field. The output modes are manifested as the superposition of edge state and bulk state, with energy spreading to other waveguides. At a specific length (L3 = 110 μm), the light-field undergoes non-adiabatic evolution: initially deviating from the edge state and later returning to the edge state. This phenomenon is termed adiabatic equivalent evolution. The output mode is localized at the edge waveguide, which is the same as the adiabatic evolution. By analyzing the fidelity between output mode and eigen edge state, we demonstrate that the adiabaticity can effectively regulate fidelity, achieving signal on/off at the edge waveguide. As structural length decreases, fidelity gradually declines and exhibits an oscillating behavior. When fidelity approaches to 1, the adiabatic equivalent evolution emerges. The first-order perturbation approximation reveals that these oscillations stem from destructive interference between edge and bulk states, thereby confirming their intrinsic origin in band interference. This mechanism enables eigen edge state output at shorter lengths than adiabatic requirements, providing a reliable approach for miniaturizing devices. Furthermore, the fabrication tolerance is analyzed. Within the whole waveguides width deviation range of –35–+30 nm (relative deviation range of –7%–+6%), the transmission of edge waveguide through the adiabatic equivalent evolution is larger than 0.9. This work analyses light-field evolution process and underlying physics for topological pumping in non-adiabatic regimes, supplements theoretical methods for analyzing non-adiabatic evolution, and provides strategies for achieving eigen edge state output at reduced lengths. This work provides some feasible principles for designing topological optical waveguide arrays, guiding the development of compact and robust on-chip photonic devices such as optical couplers and splitters, which have broad application prospects in integrated photonics.
-
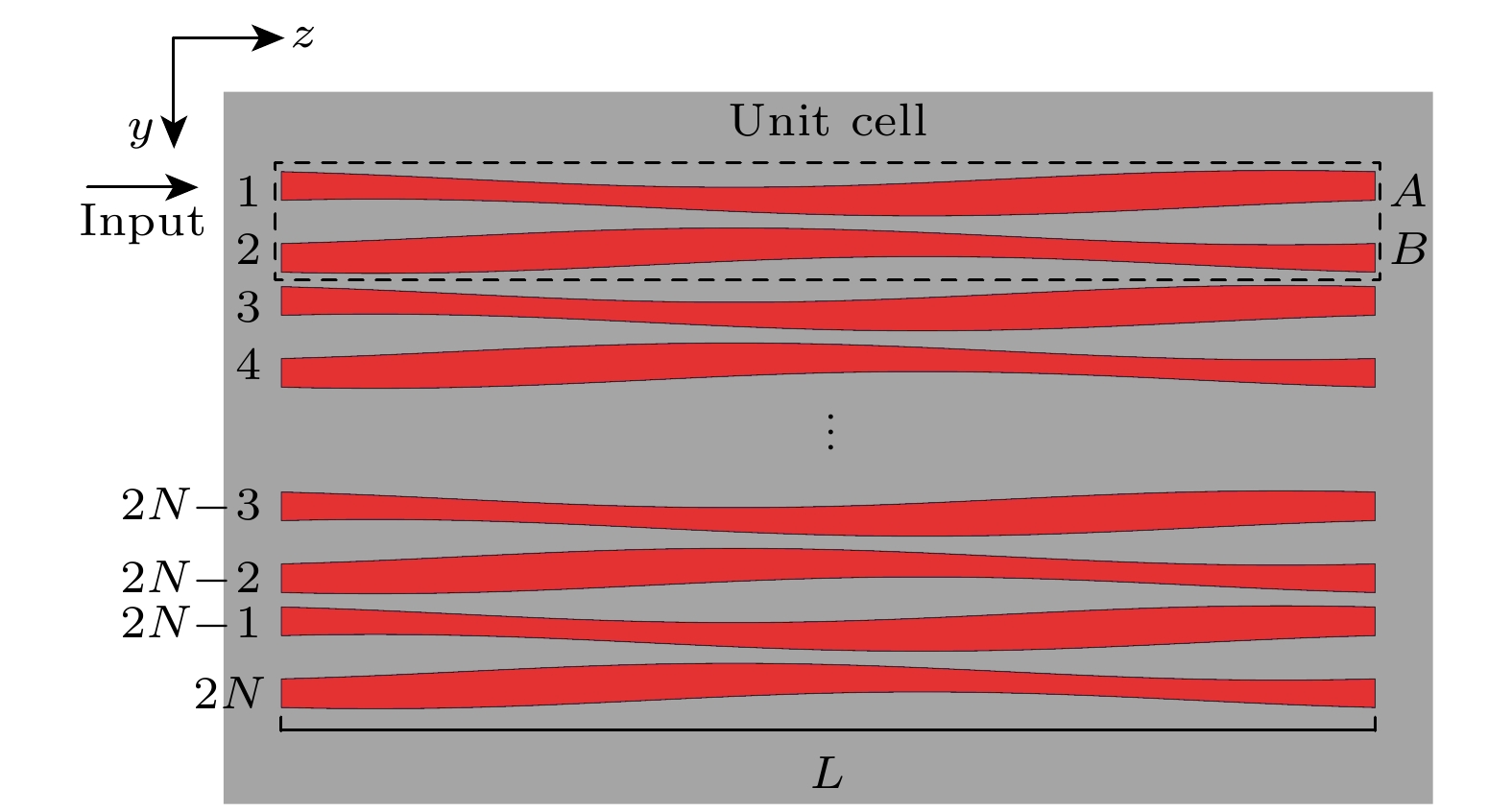
图 1 由R-M模型设置的波导阵列结构示意图. 波导结构沿z方向缓变, 沿y方向周期性排列, 一个原胞由两根波导A和B组成. L为结构长度, N为周期数, 一共有2N根波导. 光从第一根波导入射
Figure 1. Schematic diagram of the waveguide array structure configured by the R-M model. The waveguides gradually vary along the z-direction and are periodically arranged along the y-direction, with a unit cell consisting of two waveguides A and B. L represents the structure length, N represents the number of periods. The array comprises 2N waveguides. Light is incident from the first waveguide.
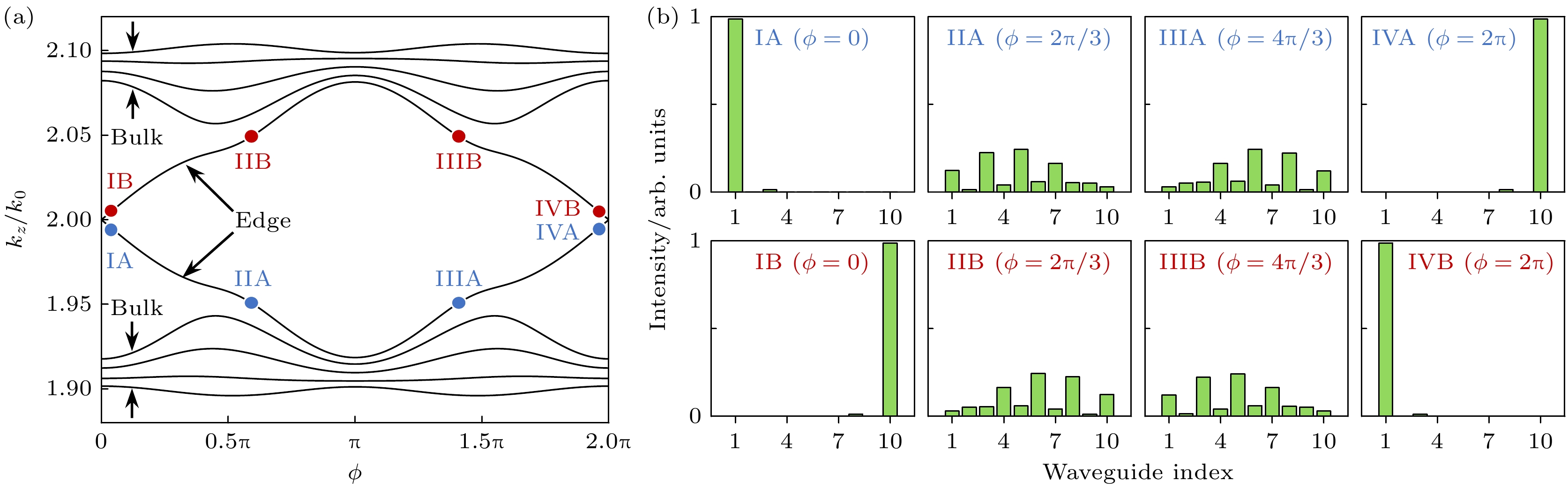
图 2 哈密顿量的能带结构及本征态 (a)当N = 5时的能带结构, kz为哈密顿量本征值, 从下至上第1—4条能带和7—10条能带对应体态, 5, 6条能带对应边界态; (b)第5, 6条能带随参数$ \varphi $演化的本征边界态. IA, IIA, IIIA和IVA分别对应第5能带四个位置的边界态, 从局域在1波导的边界态逐渐演化为局域在10波导的边界态. IB, IIB, IIIB和IVB分别对应第6能带四个位置的边界态, 从局域在10波导的边界态逐渐演化为局域在1波导的边界态
Figure 2. Band structure and eigenstates of the Hamiltonian. (a) Band structure for N = 5, where kz represents the eigenvalues of the Hamiltonian. The 1 st to 4 th and 7 th to 10 th bands (from bottom to top) correspond to bulk states, while the 5 th and 6 th bands correspond to edge states. (b) Evolution of the eigen edge states for the 5 th and 6 th bands with the parameter ϕ. IA, IIA, IIIA, and IVA denote the eigen wave function of edge states at four positions of the 5 th band. Energy transfer from waveguide 1 to waveguide 10. IB, IIB, IIIB, and IVB denote the edge states at four positions of the 6 th band, whose energy transfer from waveguide 10 to waveguide 1.
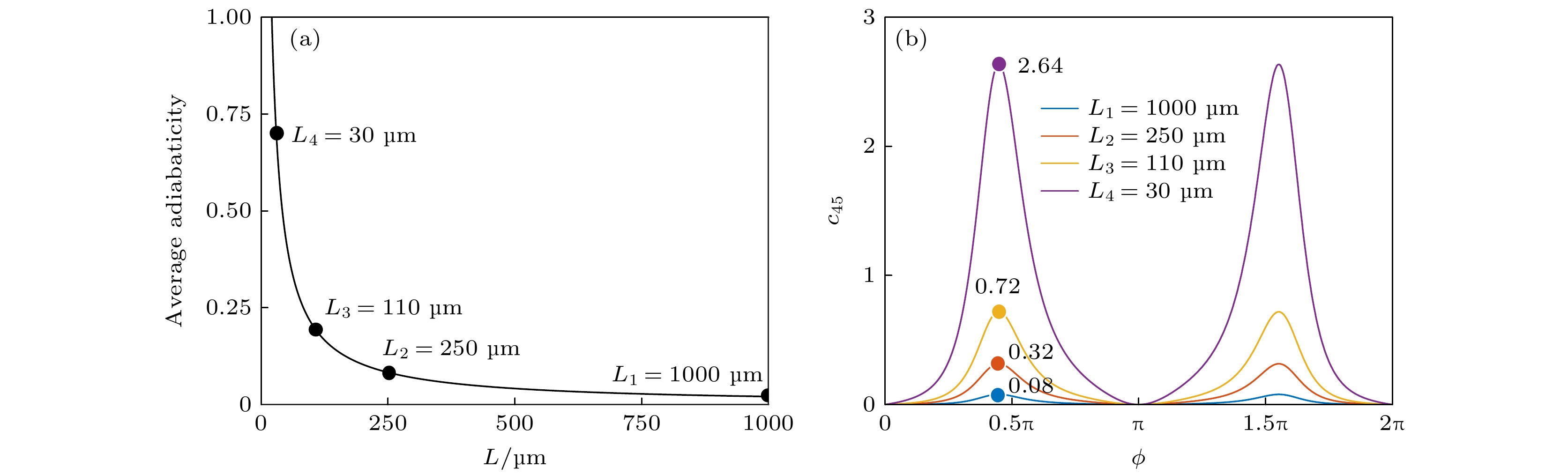
图 3 当N = 5时系统的绝热度随结构长度L的变化关系 (a)平均绝热度$ \langle c\rangle $随结构长度L的变化关系; (b)不同结构长度下绝热度c45随演化过程的变化关系
Figure 3. Adiabaticity of the system as a function of the structure length L when N = 5: (a) The average adiabaticity $\langle c\rangle $ as a function of the structure length L; (b) variation of the adiabaticity c45 during the evolution process under different structural lengths L.
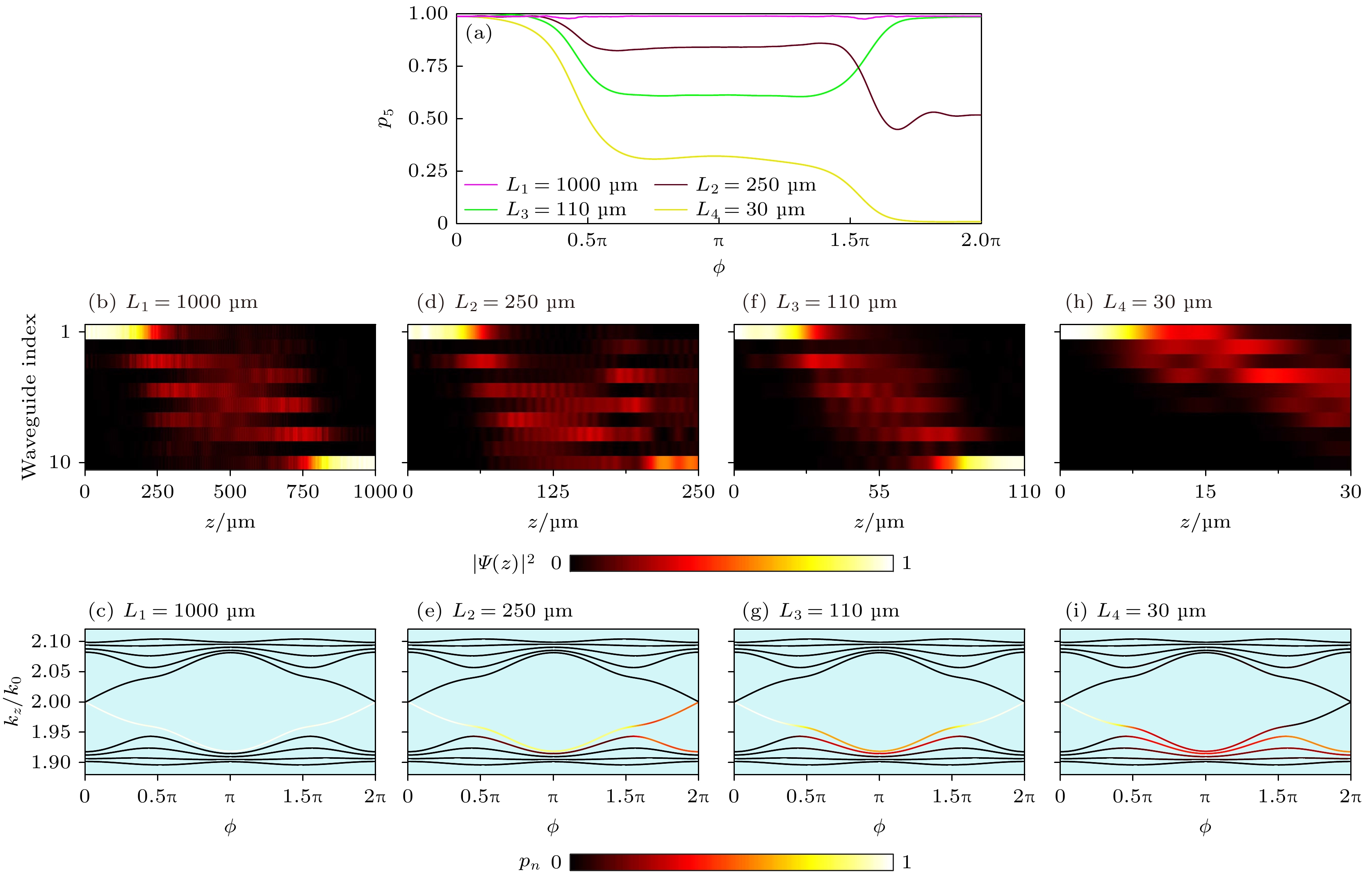
图 4 四种演化案例的光场演化过程 (a) 边界态能量占比p5的演化函数, 粉色曲线对应L1 = 1000 μm, 褐色曲线对应L2 = 250 μm, 绿色曲线对应L3 = 110 μm, 黄色曲线对应L4 = 30 μm; (b), (d), (f), (h)四种演化过程中不同波导的能量分布; (c), (e), (g), (i)四种演化过程中不同能带上的能量分布
Figure 4. Evolution of the light field for four different cases: (a) Evolution of the energy proportion of edge state p5. The pink curve corresponds to L1 = 1000 μm, brown to L2 = 250 μm, green to L3 = 110 μm, and yellow to L4 = 30 μm; (b), (d), (f), (h) energy distribution across waveguides for the four cases during evolution; (c), (e), (g), (i) energy distribution across bands for the four cases during evolution.
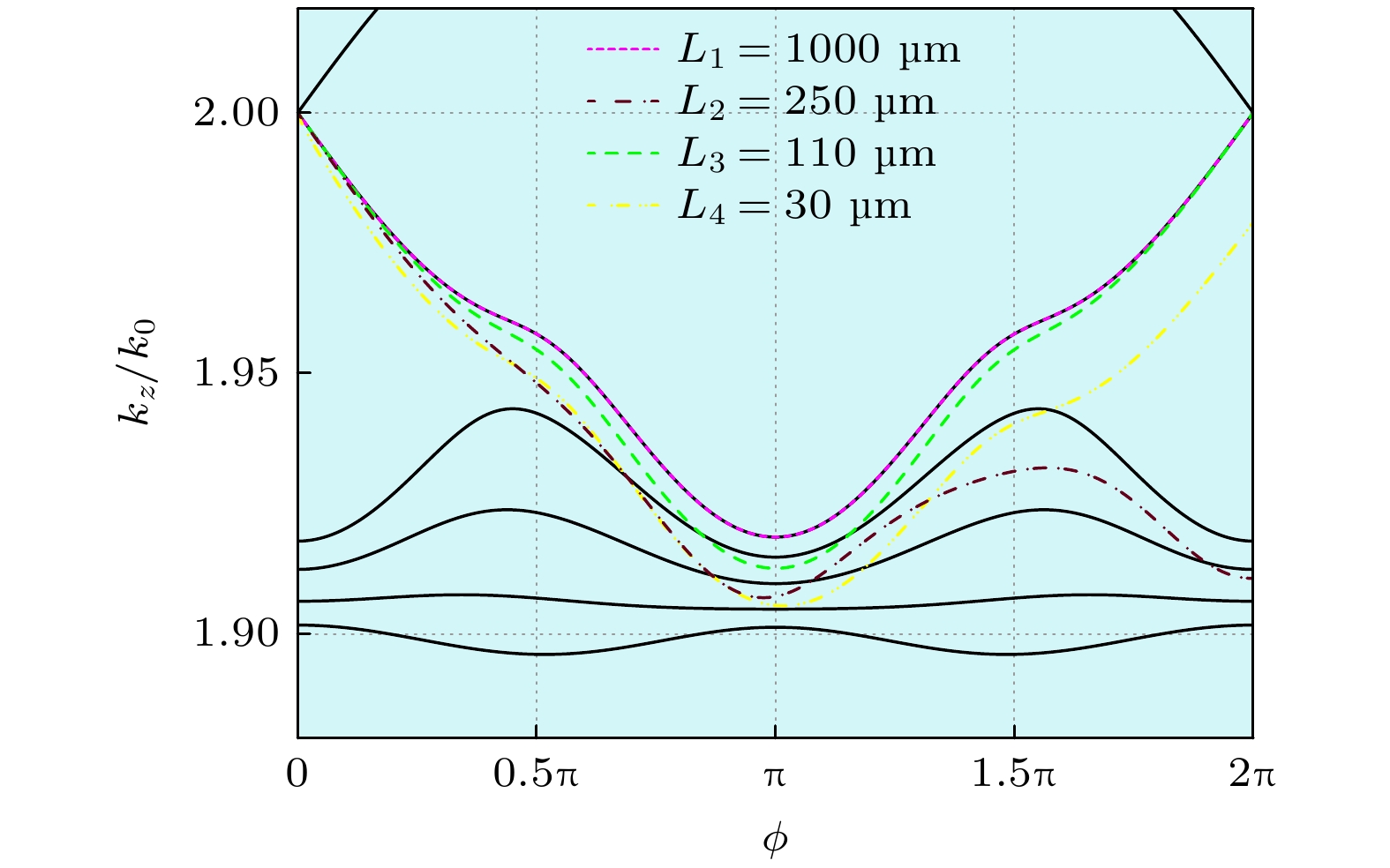
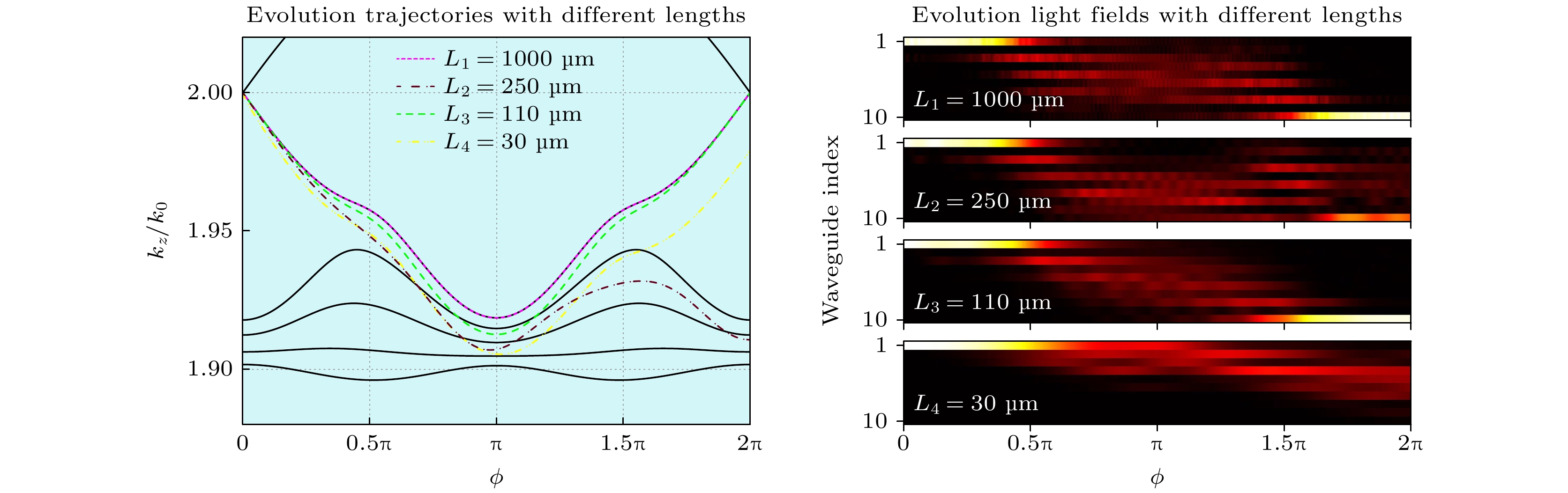
图 5 不同案例在能带上的演化轨迹示意图. 黑色曲线为哈密顿量能带, 带颜色虚线为演化轨迹示意, 粉色虚线对应绝热演化案例L1 = 1000 μm, 褐色和黄色虚线对应非绝热演化案例L2 = 250 μm和L4 = 30 μm, 绿色虚线对应等效绝热演化案例L3 = 110 μm
Figure 5. Schematic of evolution trajectories across bands for different cases. The black curves represent the band structure of the Hamiltonian, and the colored dashed lines depict the evolution trajectories. The pink dashed line corresponds to the adiabatic case for L1 = 1000 μm, while the brown and yellow dashed lines correspond to the non-adiabatic cases L2 = 250 μm and L4 = 30 μm, and the green dashed line corresponds to the adiabatic equivalent case L3 = 110 μm.
图 6 不同结构长度L对应的保真度F. 绿色五角星对应在非绝热演化范畴出现的等效绝热演化
Figure 6. The fidelity F as a function of the structure length L. The green pentagram marks the adiabatic equivalent evolution, presenting at non-adiabatic regime.
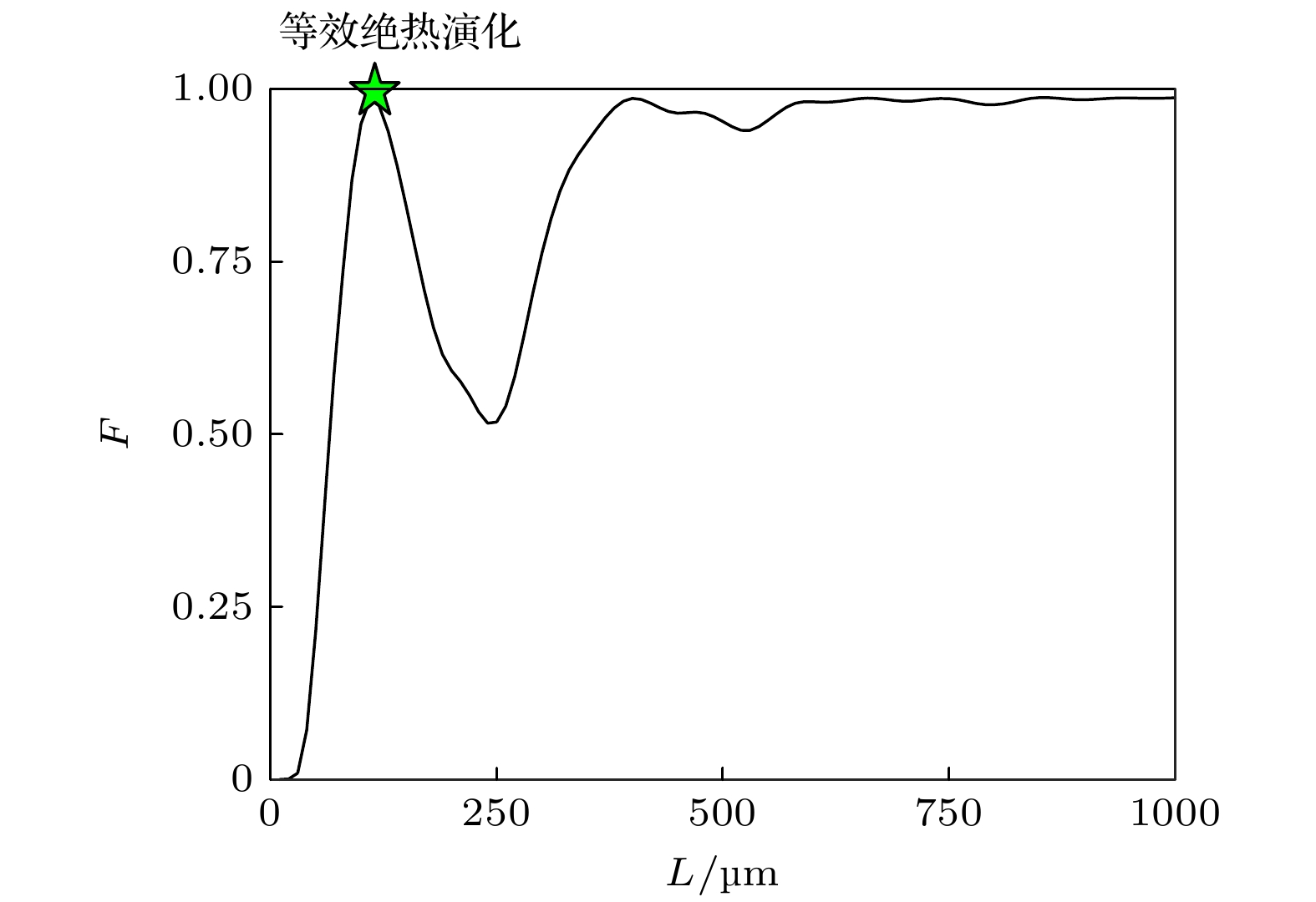
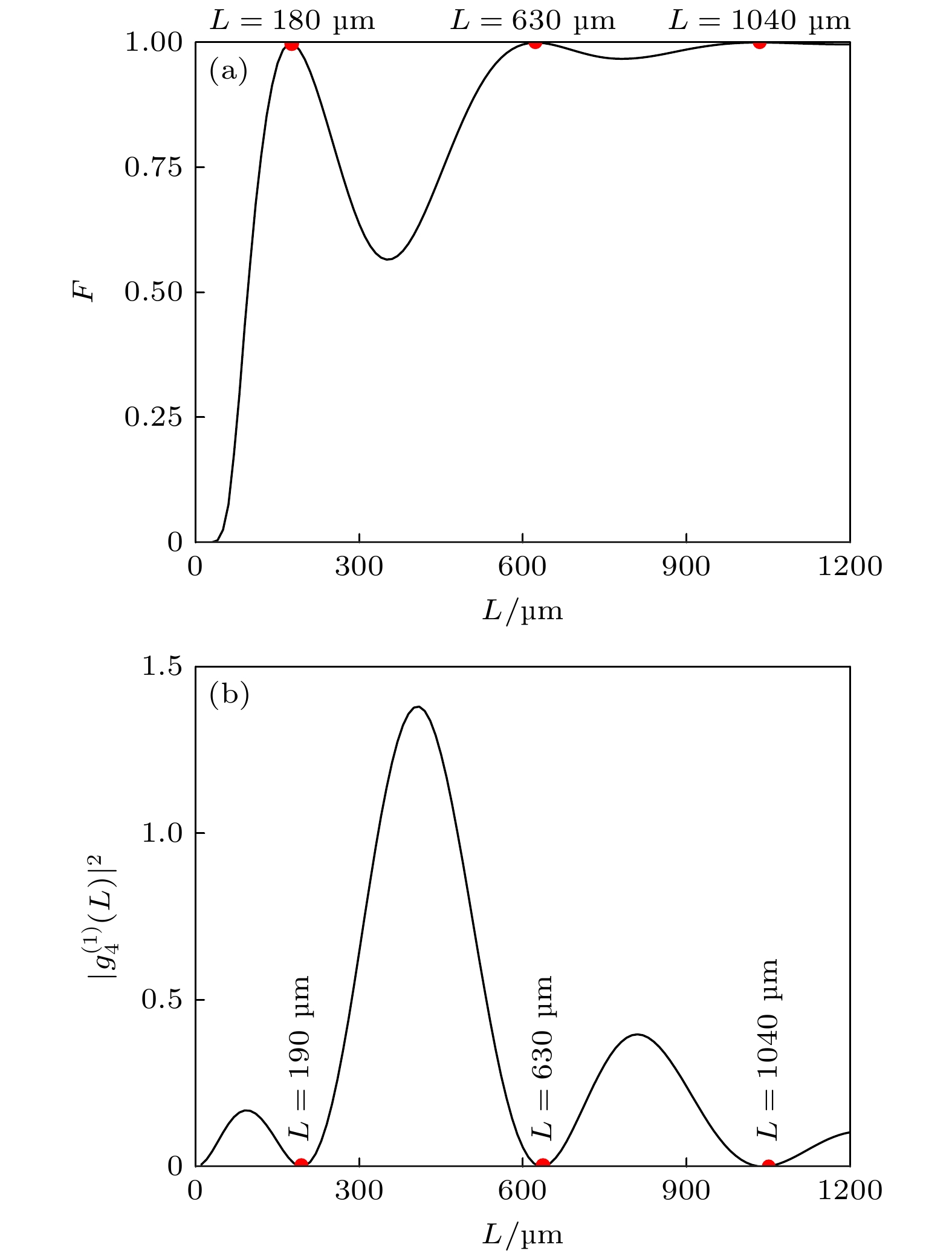
图 7 保真度F极大值和一阶微扰近似计算结果${| {g_4^{(1)}(L)} |^2}$极小值对应的位置 (a)保真度F随结构长度L的变化关系; (b) ${| {g_4^{(1)}(L)} |^2}$随结构长度L的变化关系. 红点对应极大值/极小值出现的位置
Figure 7. The positions correspond to maxima of the fidelity F and minima of the first-order perturbation approximation result ${| {g_4^{(1)}(L)} |^2}$: (a) Fidelity F as a function of the structure length L; (b) ${| {g_4^{(1)}(L)} |^2}$ as a function of the structure length L. Red dots mark the positions where the maxima/minima occur.
图 8 等效绝热演化下第10根边界波导的透射率T10随整体波导宽度误差δw的变化关系
Figure 8. The transmission of the 10th edge waveguide T10 as a function of the waveguides width deviation δw in adiabatic equivalent evolution.
-
[1] Meng Y, Chen Y Z, Lu L H, Ding Y M, Cusano A, Fan J A, Hu Q M, Wang K Y, Xie Z W, Liu Z T, Yang Y M, Liu Q, Gong M L, Xiao Q R, Sun S L, Zhang M M, Yuan X C, Ni X J 2021 Light Sci. Appl. 10 235
Google Scholar
[2] Xu H N, Dai D X, Shi Y C 2019 Laser Photonics Rev. 13 1800349
Google Scholar
[3] Xu H N, Qin Y, Hu G L, Tsang H K 2023 Laser Photonics Rev. 17 2200550
Google Scholar
[4] Shen B, Wang P, Polson R, Menon R 2015 Nat. Photonics 9 378
Google Scholar
[5] Yu Z J, Xu H N, Liu D J, Li H, Shi Y C, Dai D X 2022 J. Lightwave Technol. 40 1784
Google Scholar
[6] Zhang M, Buscaino B, Wang C, Shams-Ansari A, Reimer C, Zhu R R, Kahn J M, Lončar M 2019 Nature 568 373
Google Scholar
[7] Wu H, Tan Y, Dai D X 2017 Opt. Express 25 6069
Google Scholar
[8] Gan R F, Qi L, Ruan Z L, Liu J, Guo C J, Chen K X, Liu L 2022 Opt. Lett. 47 5200
Google Scholar
[9] Lu L, Joannopoulos J D, Soljačić M 2014 Nat. Photonics 8 821
Google Scholar
[10] Ozawa T, Price H M, Amo A, Goldman N, Hafezi M, Lu L, Rechtsman M C, Schuster D, Simon J, Zilberberg O, Carusotto I 2019 Rev. Mod. Phys. 91 015006
Google Scholar
[11] Tang G J, He X T, Shi F L, Liu J W, Chen X D, Dong J W 2022 Laser Photonics Rev. 16 2100300
Google Scholar
[12] Wang Z, Chong Y D, Joannopoulos J D, Soljačić M 2009 Nature 461 772
Google Scholar
[13] Yablonovitch E 2009 Nature 461 744
Google Scholar
[14] He X T, Liang E T, Yuan J J, Qiu H Y, Chen X D, Zhao F L, Dong J W 2019 Nat. Commun. 10 872
Google Scholar
[15] Shalaev M I, Walasik W, Tsukernik A, Xu Y, Litchinitser N M 2019 Nat. Nanotechnol. 14 31
Google Scholar
[16] Yang Y H, Yamagami Y, Yu X B, Pitchappa P, Webber J, Zhang B L, Fujita M, Nagatsuma T, Singh R 2020 Nat. Photonics 14 446
Google Scholar
[17] Sun L, Zhang Y, He Y, Wang H W, Su Y K 2020 Nanophotonics 9 1321
Google Scholar
[18] Mayer N, Ayuso D, Decleva P, Khokhlova M, Pisanty E, Ivanov M, Smirnova O 2024 Nat. Photonics 18 1155
Google Scholar
[19] He X T, Li M Y, Qiu H Y, Ruan W S, Zhou L D, Liu L, Chen X D, Chen W J, Zhao F L, Dong J W 2021 Photonics Res. 9 1423
Google Scholar
[20] Zeng Y Q, Chattopadhyay U, Zhu B F, Qiang B, Li J H, Jin Y H, Li L H, Davies A G, Linfield E H, Zhang B L, Chong Y D, Wang Q J 2020 Nature 578 246
Google Scholar
[21] Dai T X, Ma A, Mao J, Ao Y T, Jia X Y, Zheng Y, Zhai C H, Yang Y, Li Z H, Tang B, Luo J, Zhang B L, Hu X Y, Gong Q H, Wang J W 2024 Nat. Mater. 23 928
Google Scholar
[22] Thouless D J 1983 Phys. Rev. B 27 6083
Google Scholar
[23] Citro R, Aidelsburger M 2023 Nat. Rev. Phys. 5 87
Google Scholar
[24] 苑涛, 戴汉宁, 陈宇翱 2023 72 160302
Google Scholar
Yuan T, Dai H N, Chen Y A 2023 Acta Phys. Sin. 72 160302
Google Scholar
[25] 王睿琦, 李础, 李焱 2024 光学学报 44 1732012
Google Scholar
Wang R Q, Li C, Li Y 2024 Acta Opt. Sin. 44 1732012
Google Scholar
[26] Rice M J, Mele E J 1982 Phys. Rev. Lett. 49 1455
Google Scholar
[27] Sun L, Wang H W, He Y, Zhang Y, Tang G J, He X T, Dong J W, Su Y K 2022 Laser Photonics Rev. 16 2200354
Google Scholar
[28] Song W G, You O B, Sun J C, Wu S J, Chen C, Huang C Y, Qiu K, Zhu S N, Zhang S, Li T 2024 Sci. Adv. 10 eadn5028
Google Scholar
[29] Wu S J, Song W G, Sun J C, Li J, Lin Z Y, Liu X Y, Zhu S N, Li T 2024 Nat. Commun. 15 9805
Google Scholar
[30] Fedorova Z, Qiu H X, Linden S, Kroha J 2020 Nat. Commun. 11 3758
Google Scholar
[31] Privitera L, Russomanno A, Citro R, Santoro G E 2018 Phys. Rev. Lett. 120 106601
Google Scholar
[32] Liu X Y, Lin Z Y, Song W G, Sun J C, Huang C Y, Wu S J, Xiao X J, Xin H R, Zhu S N, Li T 2024 Phys. Rev. Lett. 132 016601
Google Scholar
[33] Mei F, Chen G, Tian L, Zhu S L, Jia S T 2018 Phys. Rev. A 98 012331
Google Scholar
[34] Qi L, Wang G L, Liu S T, Zhang S, Wang H F 2020 Phys. Rev. A 102 022404
Google Scholar
[35] Martínez-Garaot S, Ruschhaupt A, Gillet J, Busch T, Muga J G 2015 Phys. Rev. A 92 043406
Google Scholar
DownLoad:
Metrics
- Abstract views: 320
- PDF Downloads: 8
- Cited By: 0
