-
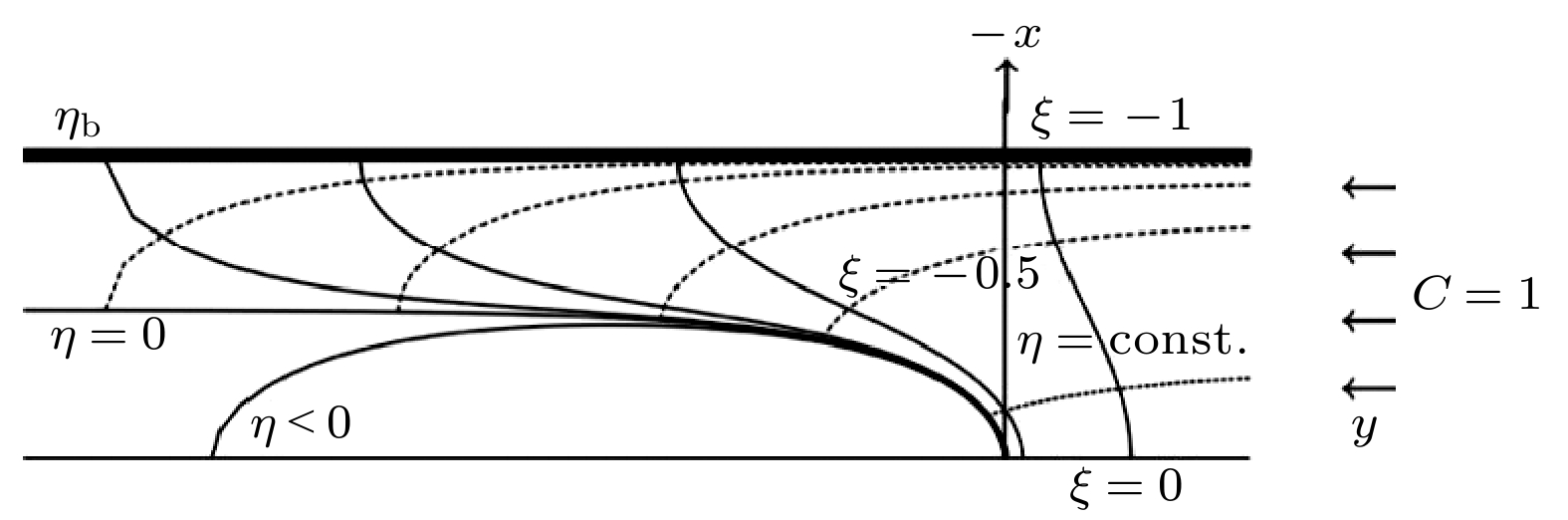
Directional solidification technology artificially controls the propagation rate at the solid-liquid interface to promote the development of the metal microstructure in the expected direction. In the process, the solid-liquid interface will produce complex and diverse microstructures, of which cellular crystal and dendritic structure are typical microstructures in the interface formation process, which have a direct influence on the quality and properties of the final material. Based on the fact that the far-field flow is not strongly affected by local perturbations and has the characteristics of relative stability and homogeneity, a mathematical model including the temperature field, the concentration field and the far field flow is established in this work. According to the interfacial wave theory, a finger coordinate system is constructed using the constant solution of cellular crystal growth as the ground state, and fast variables are introduced for variable replacement using multivariate expansion method and matched asymptotic expansion method used to introduce. The eigenvalue problem of linear perturbation dynamics in the case of far-field flow is solved, and the dispersion relation of the change rate of the perturbation amplitude at the interface of the cellular crystal and the quantization condition of the interface morphology are derived. The stability of the growth of deep cellular crystal in directional solidification under the action of far-field flow is analyzed. and the basis for judging the critical stability of the deep cellular crystal growth is established. The effect of far-field flow on the size of the unstable region is revealed. The results show that in the directional solidification considering the far-field flow, there are two overall instability mechanisms for the interfacial morphology of the growth of deep cellular crystal: the global oscillatory instability (GTW-mode) and the low-frequency instability (IF-mode). The system allows of the symmetric S-mode and the antisymmetric A-mode. The stability analysis shows the following points: the interfacial stability of deep cellular crystal depends on the critical stability parameter; if the interfacial stability parameter of deep cellular crystal is larger than the critical stability parameter, the growth of deep cellular crystal is stable; if it is smaller than the critical stability parameter, the growth of deep cellular crystal is unstable, whereas the critical stability parameter decreases with the enhancement of the flow intensity. Under the influence of far field flow, for the same index n, the growth rate of the GTW-S mode is much greater than that of the GTW-A mode, which is said to be more dangerous than the GTW-A mode, and the n = 0 case in the GTW-S mode is the most dangerous oscillation mode with the largest unstable region. In addition, as the flow intensity Gu increases, the stable region of the overall oscillatory instability of the dendritic structure, where the neutral mode generates strong oscillations, also becomes larger. -
Keywords:
- deep cellular crystal growth /
- far field flow /
- interface stability /
- quantization condition
-
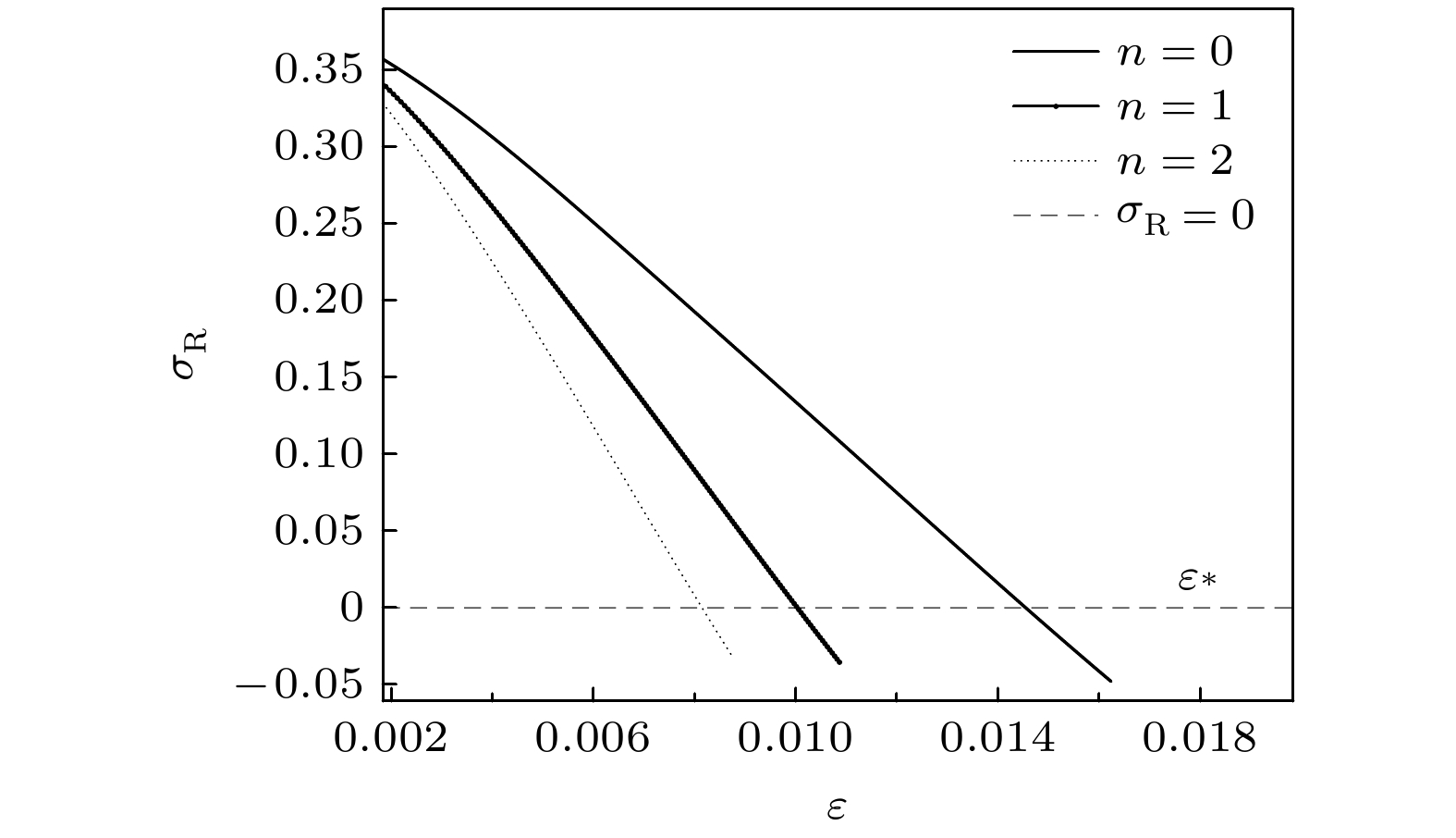
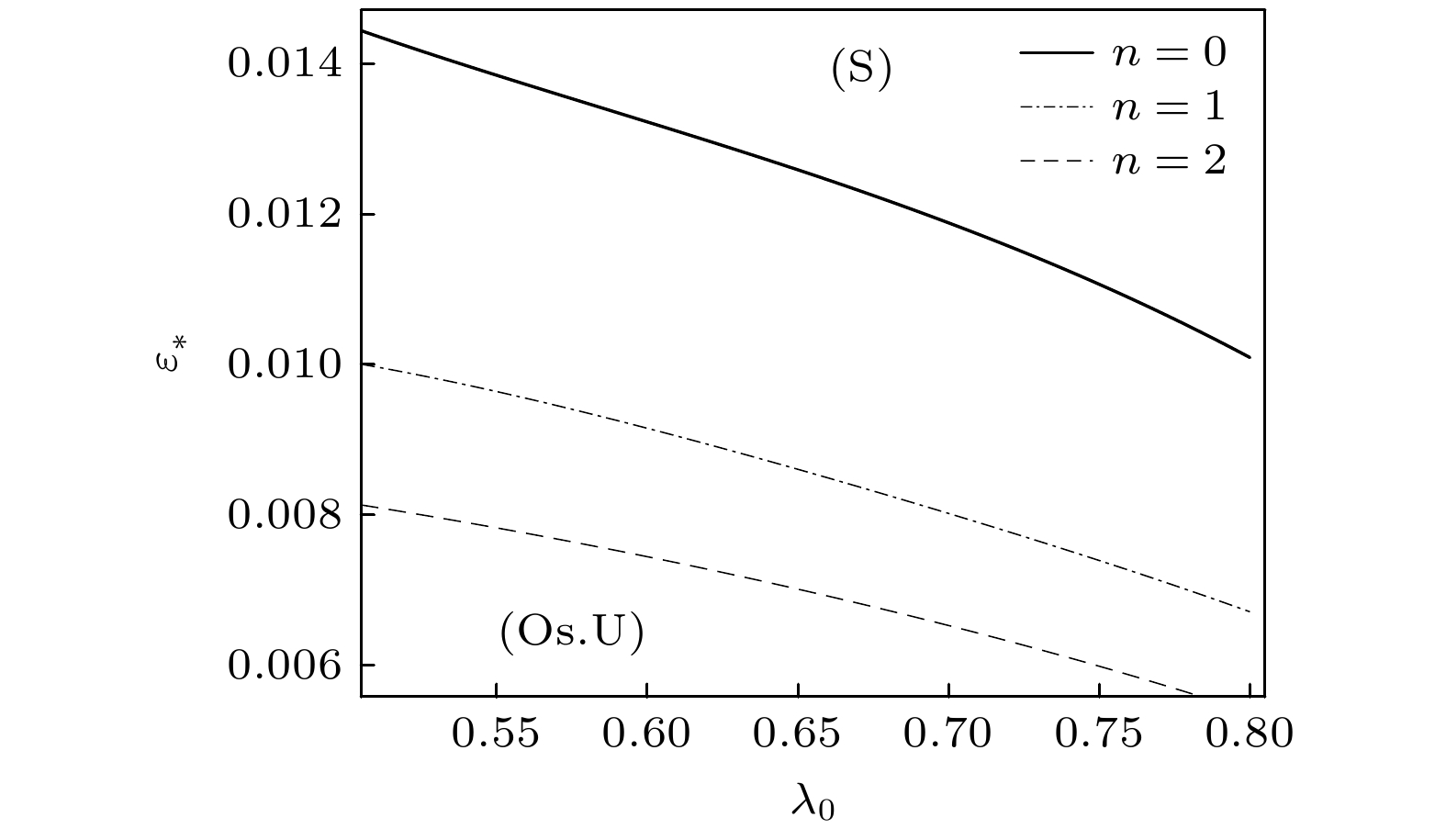
图 3 GTW-S模式的特征值的实部随$ \varepsilon $的变化曲线. 参数分别为$ n = 0, {\text{ 1, 2, }} $$ \kappa = 0.3, $$ Gu = 0.1, $ $ {\lambda _{\text{G}}} = 0.2, $ $ {G_{\text{c}}} =2.0 \times $$ {10^{ - 5}}, $ $ {\varepsilon _{\text{c}}} = 0.01, $ $ M = 0.08, $ $ {\lambda _0} = 0.45, $ $ {W_0} = 2.1332$
Figure 3. The real parts of the eigenvalues of the GTW-S mode variation with $ \varepsilon $. With the parameters $ n = 0, {\text{ 1, 2, }} $ $ \kappa = 0.3, $ $ Gu = 0.1, $$ {\lambda _{\text{G}}} = 0.2, $ $ {G_{\text{c}}} = 2.0 \times {10^{ - 5}}, $ $ {\varepsilon _{\text{c}}} = 0.01, $ $ M = 0.08, $ $ {\lambda _0} = 0.45 $ and $ {W_0} = 2.1332 $.
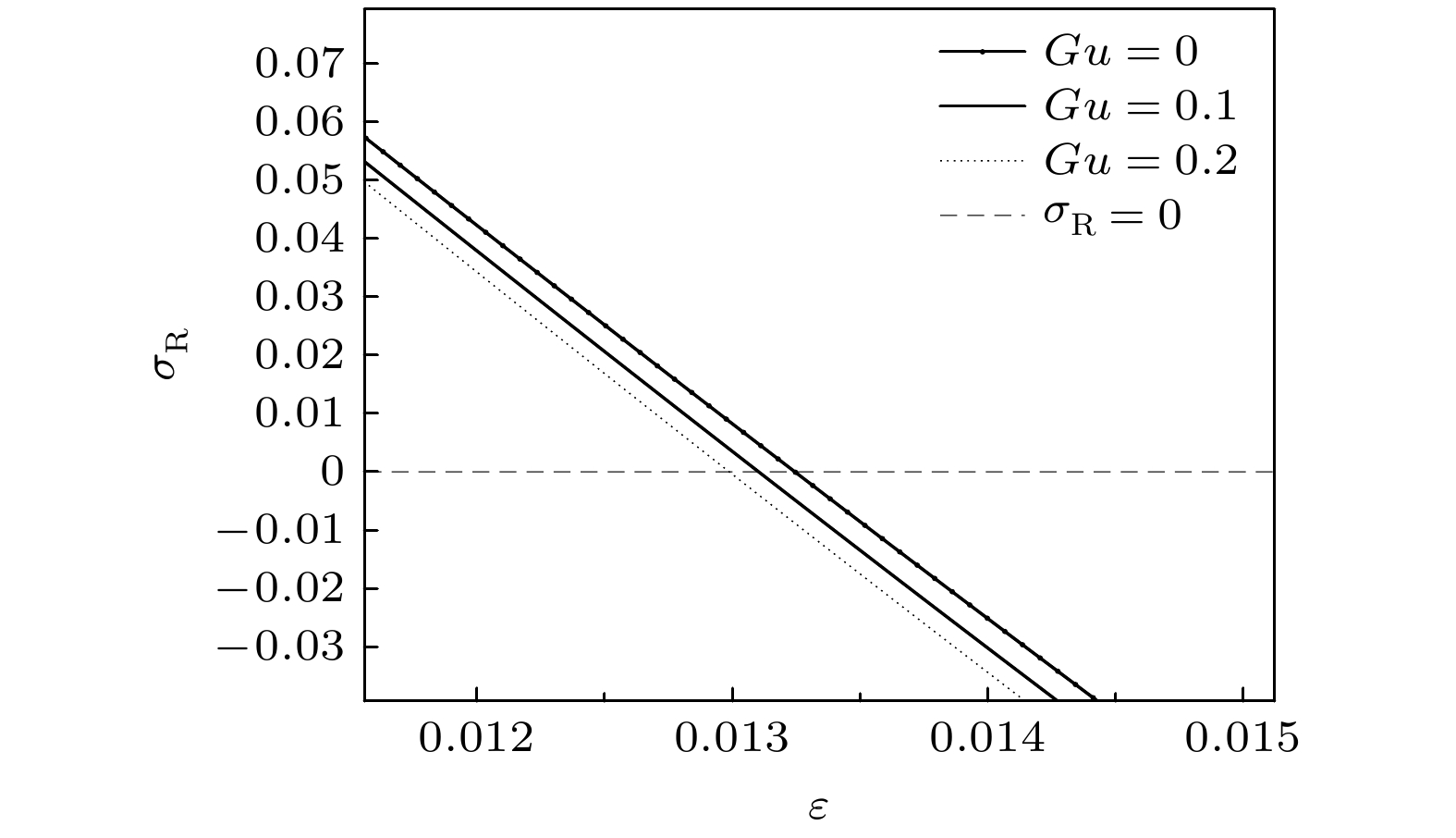
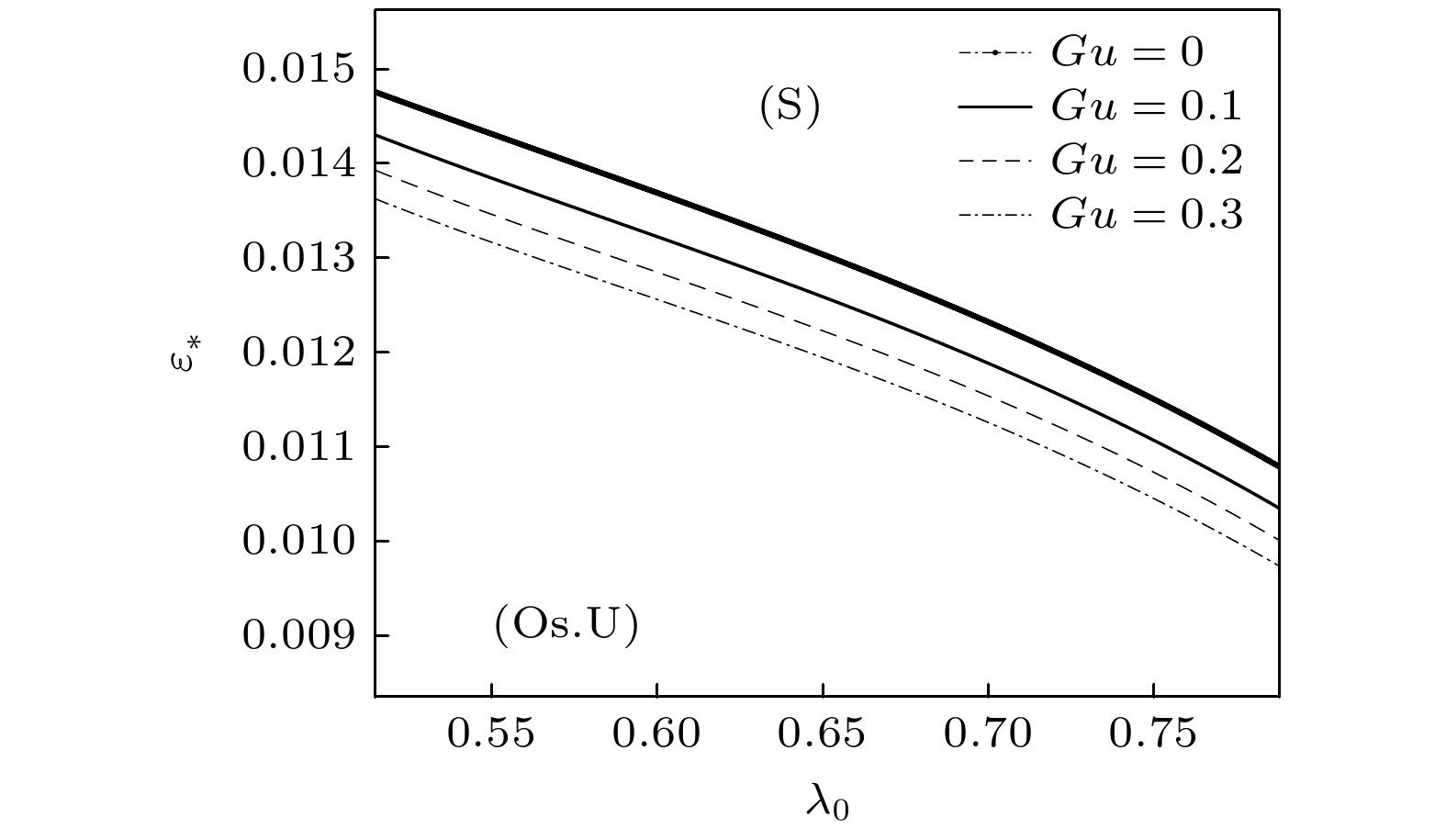
图 4 GTW-S模式的特征值的实部随$ \varepsilon $的变化曲线. 参数分别为$ n = 0, $$ \kappa = 0.3, $$ Gu = 0, {0}{.1}, {0}{.2}, $$ {\lambda _{\text{G}}} = 0.2, $$ {G_{\text{c}}} = $$ 2.0 \times {10^{ - 5}}, $$ {\varepsilon _{\text{c}}} = 0.01, $$ M = 0.08, $$ {\lambda _0} = 0.45, $ $ {W_0} = 2.1332 $$
Figure 4. The real parts of the eigenvalues of the GTW-S mode variation with $ \varepsilon $. With the parameters $ n = 0, $ $ \kappa = 0.3, $ $ Gu = 0, {\text{ }}0.1, {\text{ }}0.2, $ $ {\lambda _{\text{G}}} = 0.2, $ $ {G_{\text{c}}} = 2.0 \times {10^{ - 5}}, $ $ {\varepsilon _{\text{c}}} = 0.01, $ $ M = 0.08, $ $ {\lambda _0} = 0.45 $ and $ {W_0} = 2.1332 $.
图 5 零级近似GTW-S 中性模式曲线. 参数分别为$ n = $$ 0, {\text{ 1, 2, }} $ $ \kappa = 0.29, $ $ Gu = 0.1, $ $ {\lambda _{\text{G}}} = 0.4989, $ $ {G_{\text{c}}} =0.14485 \times $$ {10^{ - 4}}, $ $ {\varepsilon _{\text{c}}} = 0.5388 \times {10^{ - 2}}, $ $ M = 0.9552 \times {10^{ - 1}} $
Figure 5. The neutral curves of the GTW-S-modes in zeroth-order approximation for the case $ n = 0, {\text{ 1, 2, }} $ $ \kappa = 0.29, $ $ Gu = 0.1, $ $ {\lambda _{\text{G}}} = 0.4989, $ $ {G_{\text{c}}} = 0.14485 \times {10^{ - 4}}, $ $ {\varepsilon _{\text{c}}} = $$ 0.5388 \times {10^{ - 2}}, $ $ M = 0.9552 \times {10^{ - 1}} $.
图 6 一级近似GTW-S 中性模式曲线. 参数分别为$ n = 0, {\text{ 1, 2, }} $ $ \kappa = 0.29, $ $ Gu = 0.1, $ $ {\lambda _{\text{G}}} = 0.4989, $ $ {G_{\text{c}}} = $$ 0.14485 \times {10^{ - 4}}, $ $ {\varepsilon _{\text{c}}} = 0.5388 \times {10^{ - 2}}, $ $ M = 0.9552 \times {10^{ - 1}} $$
Figure 6. The neutral curves of the GTW-S-modes with first-order approximation for the case $ n = 0, {\text{ 1, 2, }} $ $ \kappa = 0.29, $ $ Gu = 0.1, $ $ {\lambda _{\text{G}}} = 0.4989, $ $ {G_{\text{c}}} = 0.14485 \times {10^{ - 4}}, $ $ {\varepsilon _{\text{c}}} = $$ 0.5388 \times {10^{ - 2}}, $ $ M = 0.9552 \times {10^{ - 1}} $
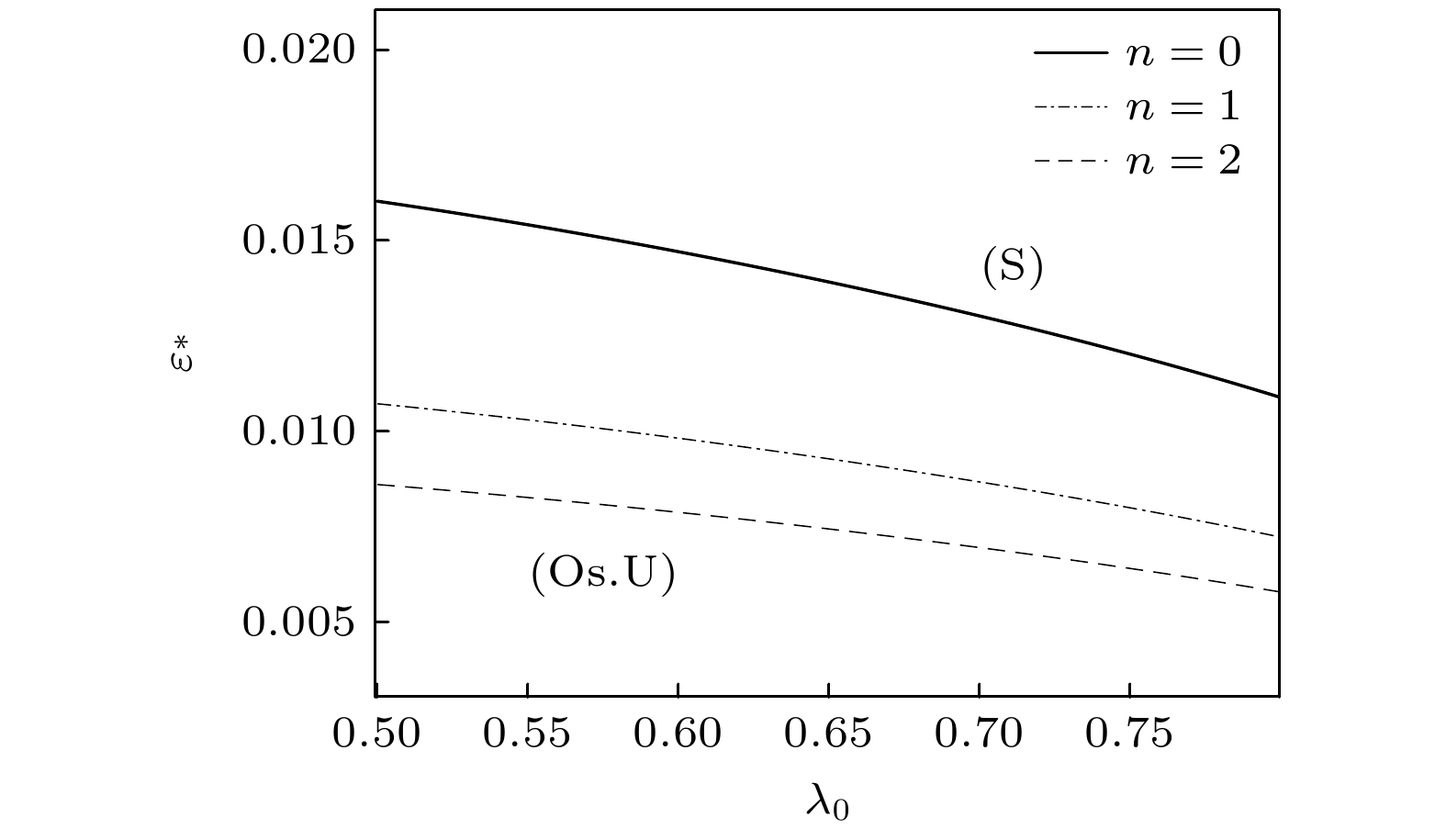
图 7 一级近似GTW-S 中性模式曲线$ \left( {n = 0} \right) $. 参数分别为$ Gu = 0, {\text{ }}0.1, {0}{.2}, {\text{ }}0.3, $ $ n = 0, $ $ {\lambda _{\text{G}}} = 0.4989, $ $ {G_{\text{c}}} = $$ 0.14485 \times {10^{ - 4}}, $ $ {\varepsilon _{\text{c}}} = 0.5388 \times {10^{ - 2}}, $ $ \kappa = 0.29, $ $ M = $$ 0.9552 \times {10^{ - 1}} $
Figure 7. The neutral curves of the GTW-S-modes $ \left( {n = 0} \right) $ with first-order approximation for the case $ Gu =0, $$ 0.1, {0.2}, {\text{ }}0.3, $$ n = 0, $ $ {\lambda _{\text{G}}} = 0.4989, $ $ {G_{\text{c}}} = 0.14485 \times {10^{ - 4}}, $ $ {\varepsilon _{\text{c}}} = 0.5388 \times {10^{ - 2}}, $ $ \kappa = 0.29, $ $ M = 0.9552 \times {10^{ - 1}} $
-
[1] Mullins W W, Sekerka R F 1963 J. Appl. Phys. 34 323
 Google Scholar
Google Scholar
[2] Mullins W W, Sekerka R F 1964 J. Appl. Phys. 35 444
 Google Scholar
Google Scholar
[3] 王自东, 胡汉起 1997 中国科学: E辑 27 102
Wang Z D, Hu H Q 1997 Science in China (Series E) 27 102
[4] 王自东, 周永利, 常国威, 胡汉起 1999 中国科学: E辑 29 1
Wang Z D, Zhou Y L, Chang G W, Hu H Q 1999 Science in China(Series E) 29 1
[5] Pelcé P, Pumir A 1985 J. Cryst. Growth 73 337
 Google Scholar
Google Scholar
[6] Pocheau A, Georgelin M 2003 J. Cryst. Growth 250 100
 Google Scholar
Google Scholar
[7] Pocheau A, Georgelin M 2004 J. Cryst. Growth 268 272
 Google Scholar
Google Scholar
[8] Pocheau A, Georgelin M 2006 Phys. Rev. E 73 011604
 Google Scholar
Google Scholar
[9] Georgelin M, Bodea S, Pocheau A 2007 Europhys. Lett. 77 46001
 Google Scholar
Google Scholar
[10] Xu J J 1991 Phys. Rev. A 43 930
 Google Scholar
Google Scholar
[11] Xu J J 1991 Eur. J. Appl. Math. 2 105
 Google Scholar
Google Scholar
[12] Xu J J 1997 Nonlinear Anal. Theory Methods Appl. 30 2775
 Google Scholar
Google Scholar
[13] Chen Y Q, Xu J J 2011 J. Cryst. Growth 318 32
 Google Scholar
Google Scholar
[14] Xu J J, Chen Y Q 2011 Phys. Rev. E 83 061605
[15] Saffman P G, Taylor G I 1958 Proc. R. Soc. London, Ser. A 245 312
 Google Scholar
Google Scholar
[16] 蒋晗, 陈明文, 史国栋, 王涛, 王自东 2016 65 096803
 Google Scholar
Google Scholar
Jiang H, Chen M W, Shi G D, Wang T, Wang Z D 2016 Acta Phys. Sin. 65 096803
 Google Scholar
Google Scholar
[17] 孙思杰, 蒋晗 2024 73 118101
 Google Scholar
Google Scholar
Sun S J, Jiang H 2024 Acta Phys. Sin. 73 118101
 Google Scholar
Google Scholar
[18] Fan H L, Chen M W, Shan Y Y 2020 Surf. Rev. Lett. 27 1950170
 Google Scholar
Google Scholar
[19] 曹斌, 林鑫, 黄卫东 2011 60 066403
 Google Scholar
Google Scholar
Cao B, Lin X, Huang W D 2011 Acta Phys. Sin. 60 066403
 Google Scholar
Google Scholar
[20] 李向明, 陈明文, 王自东 2008 北京科技大学学报 30 652
Li X M, Chen M W, Wang Z D 2008 J. Univ. Sci. Technol. Beijing. 30 652
[21] 王建元, 翟薇, 金克新, 陈长乐 2011 60 098106
 Google Scholar
Google Scholar
Wang J Y, Zhai W, Jin K X, Chen C L 2011 Acta Phys. Sin. 60 098106
 Google Scholar
Google Scholar
[22] 王贤斌, 林鑫, 王理林, 宇红雷, 王猛, 黄卫东 2013 62 078102
 Google Scholar
Google Scholar
Wang X B, Lin X, Wang L L, Yu H L, Wang M, Huang W D 2013 Acta Phys. Sin. 62 078102
 Google Scholar
Google Scholar
[23] Pandit K, Upadhyay S R, Tewari S N 2018 J. Cryst. Growth 502 19
 Google Scholar
Google Scholar
[24] Trivedi R, Miyahara H, Mazumder P, Simsek E, Tewari S N 2001 J. Cryst. Growth 222 365
 Google Scholar
Google Scholar
[25] 曾红波, 艾新港, 陈明, 王敏, 蒋加旋 2023 工程科学学报 45 541
Zeng H B, Ai X G, Chen M, Wang M, Jiang J X 2023 Chin. J. Eng. 45 541
[26] Zheng G J, Chen M W 2021 J. Eng. Math. 130 12
 Google Scholar
Google Scholar
[27] Chen M W, Jiang J X, Li L Y, Wang Z D 2022 Metals 12 1487
 Google Scholar
Google Scholar
[28] 刘竞, 陈明文 2012 宁夏大学学报(自然科学版) 33 167
Liu J, Chen M W 2012 J. Ningxia Univ. (Nat. Sci. Ed. ) 33 167
[29] 刘焕珍 2024 硕士学位论文 (桂林: 桂林电子科技大学)
Liu H Z 2024 M. S. Thesis (Guilin: Guilin University of Electronic Technology
Metrics
- Abstract views: 251
- PDF Downloads: 1
- Cited By: 0














 DownLoad:
DownLoad: