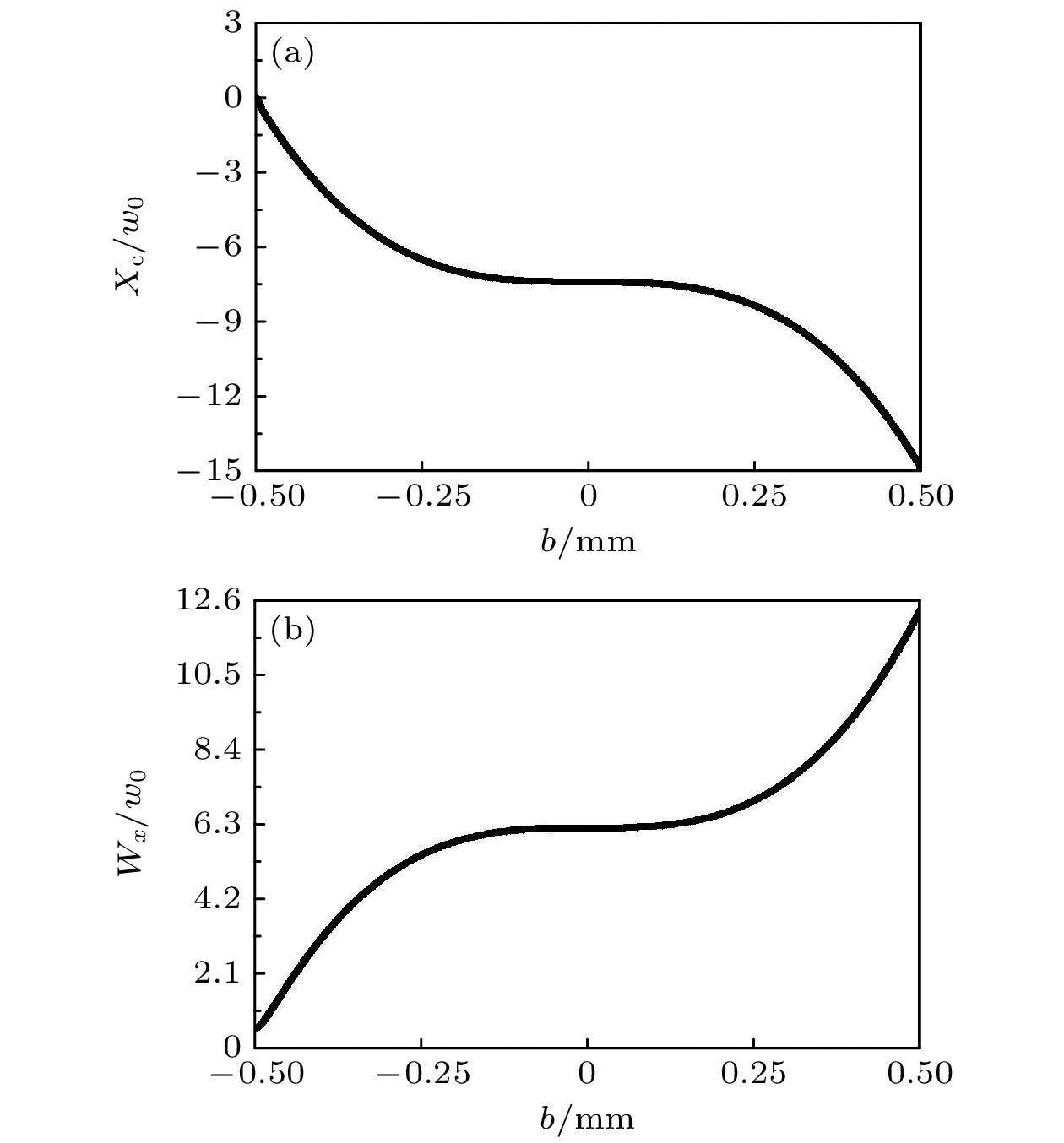
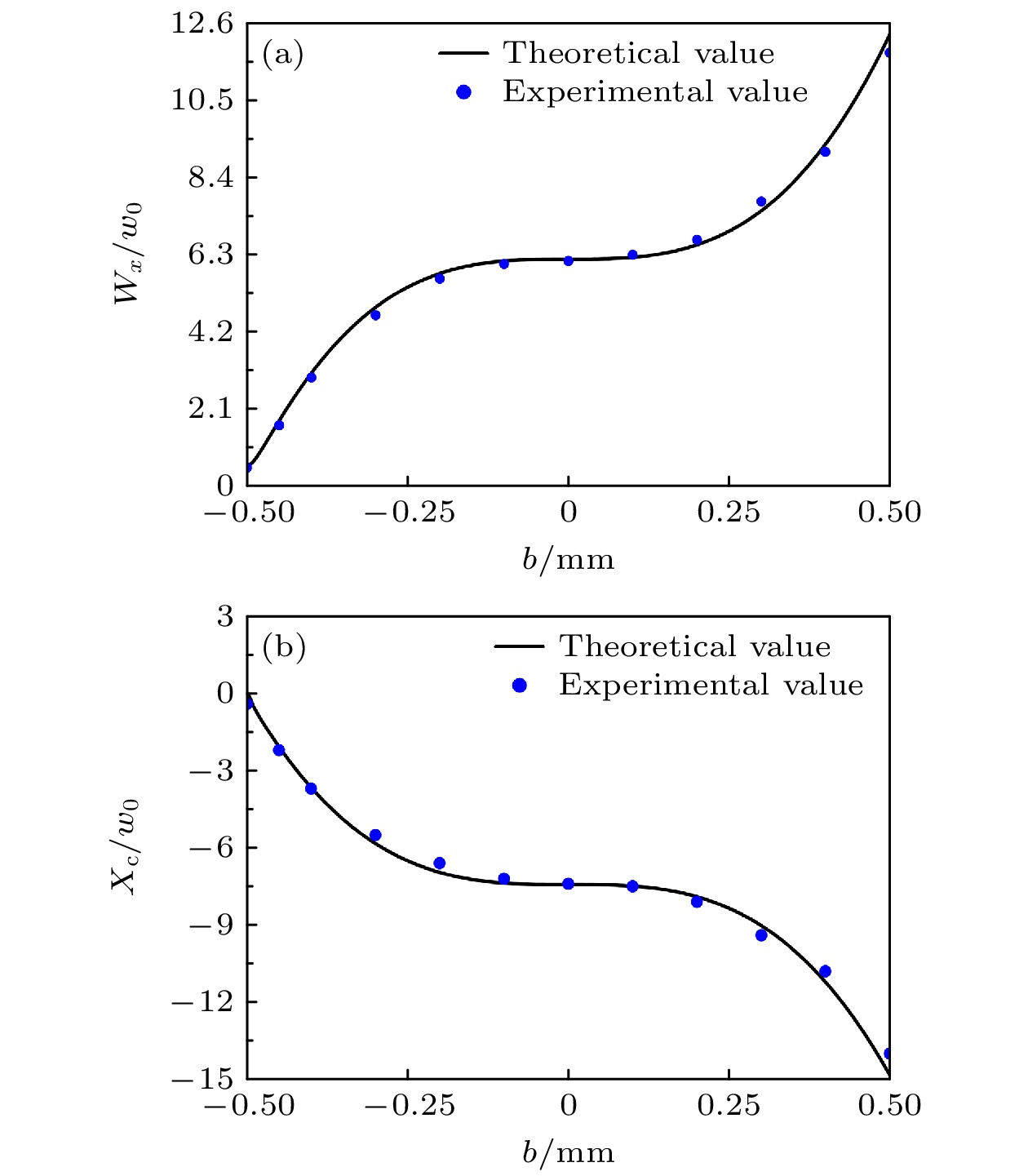
-
As a remarkable optical transformation enabling mutual conversion between Gaussian and Airy beams, the Airy transformation raises intriguing questions when applied to Airyprime beam—an advanced variant of conventional Airy beam. To answer these questions, numerical simulations and experimental verification are combined in this study. The results show two different operation regimes: when the Airy coefficient exceeds the negative transverse scale factor, the Airy-transformed optical field of Airyprime beam in any transverse direction becomes equivalent to the superposition of eccentric Airy beam and eccentric Airyprime beam; when the Airy coefficient equals the negative transverse scale factor, the transformed optical field equivalently corresponds to the sum of two displaced elegant Hermite-Gaussian beams. Analytical expressions for centroid and beam half width under both regimes are rigorously derived and validated experimentally by using Airy transformation of Airyprime beams to systematically measure the influences of Airy coefficientson intensity distribution, centroid displacement, and beam half width. This investigation provides a novel method for generating complex beam profiles while enhancing the potential application value of such beams in optical communication and beam-splitting technology.
-
Keywords:
- Airyprime beam /
- Airy transformation /
- Airy coefficients /
- centroid /
- beam half width
-
图 1 艾里变换示意图
Figure 1. A diagrammatic sketch of Airy transformation.
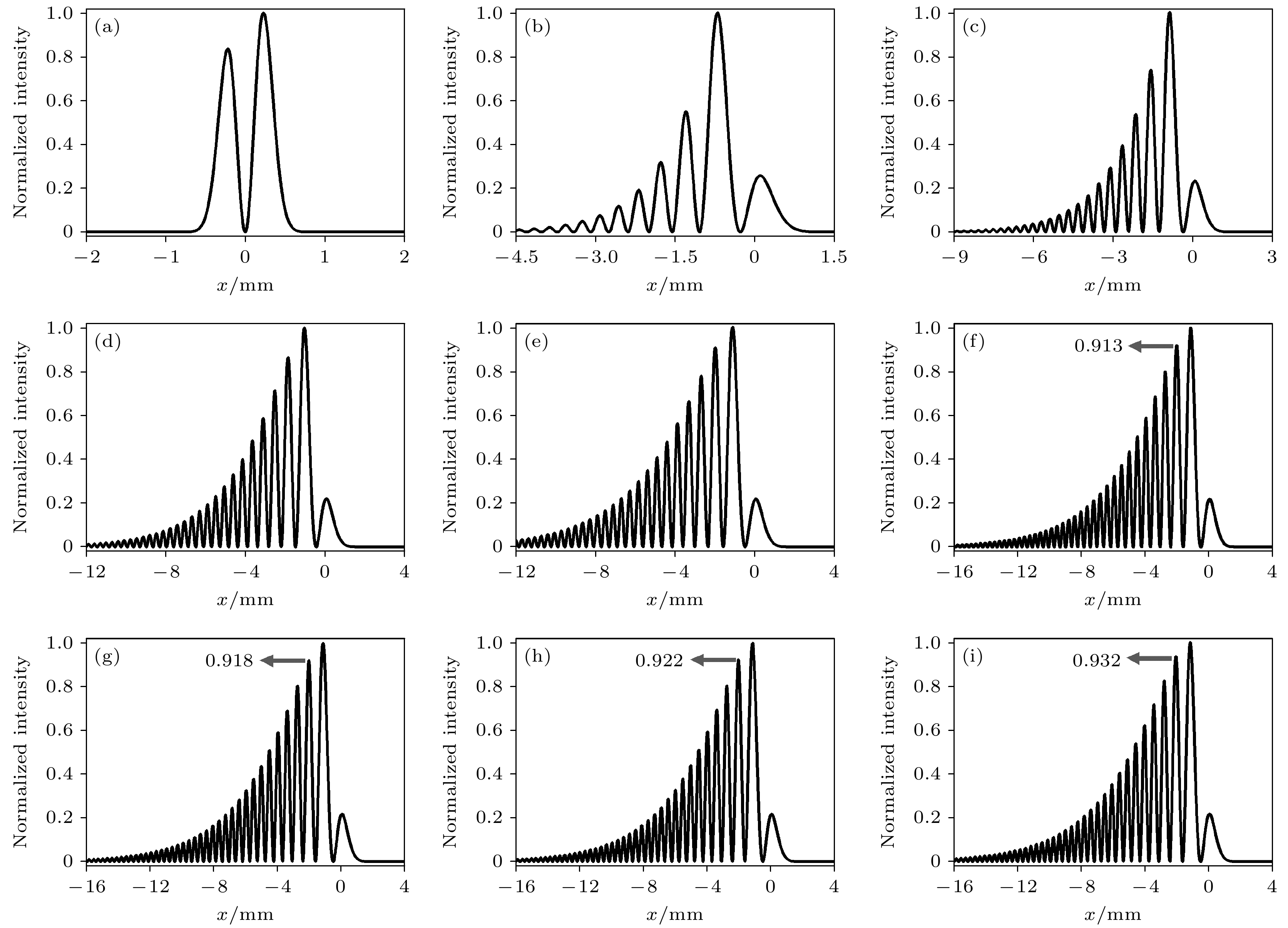
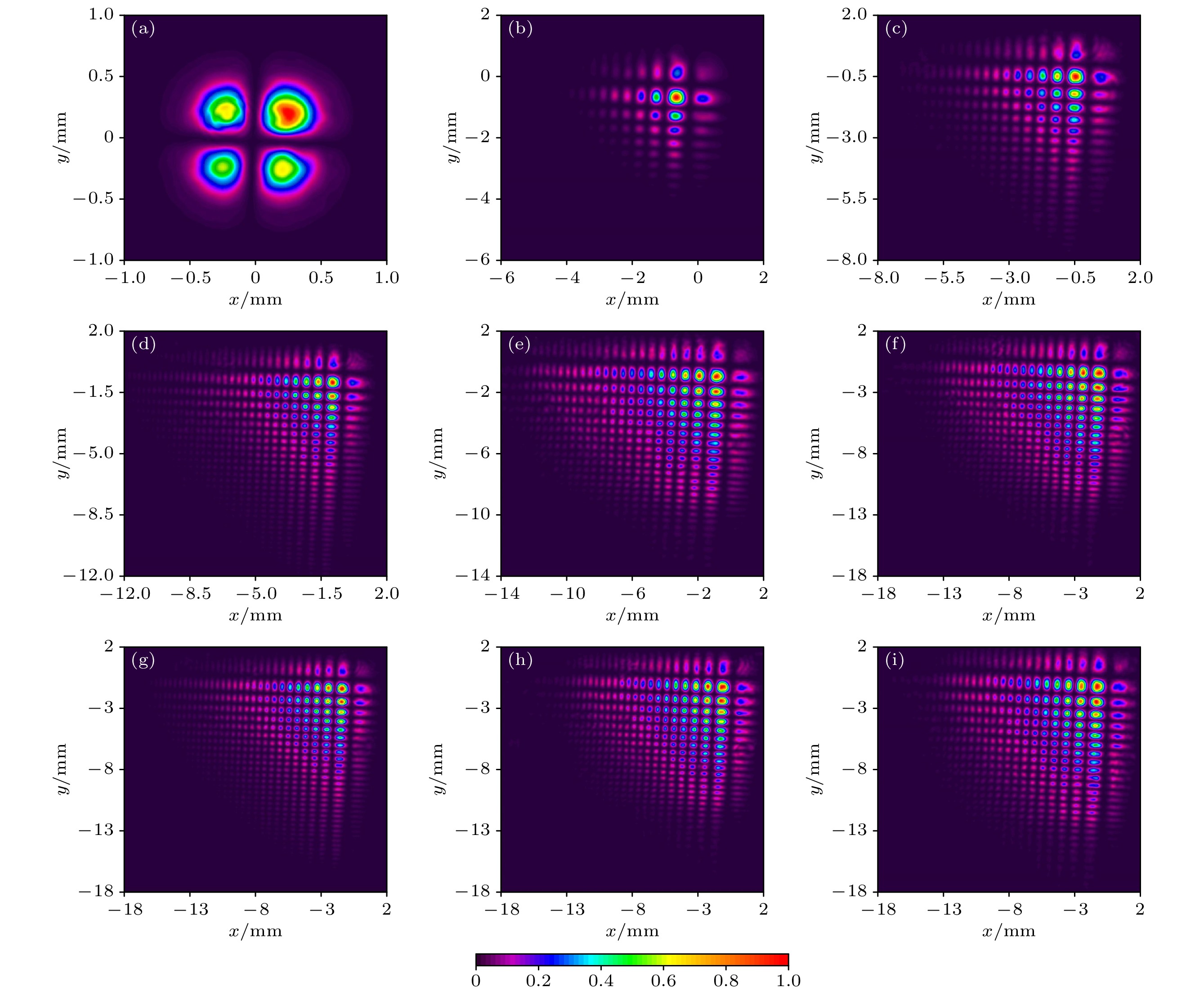
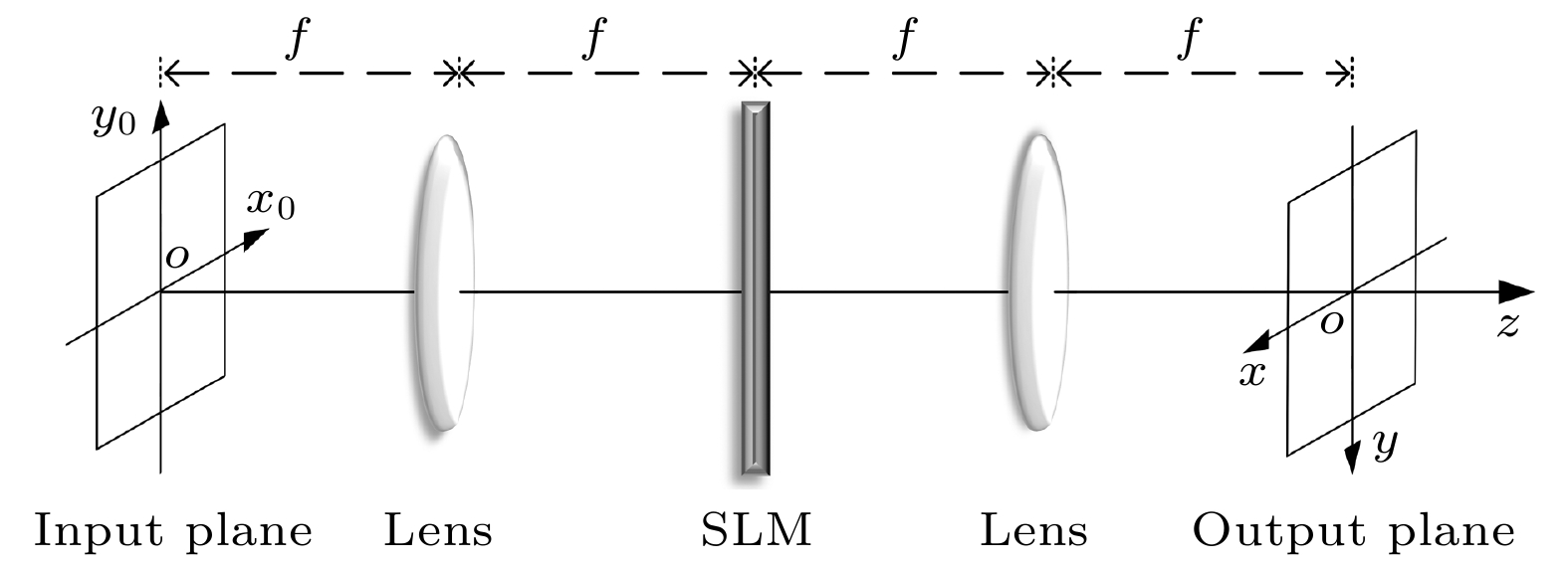
图 2 一阶艾里导数光束经不同艾里变换后x方向上的归一化光强分布 (a) b = –0.50 mm; (b) b = –0.45 mm; (c) b = –0.40 mm; (d) b = –0.30 mm; (e) b = –0.20 mm; (f) b = –0.10 mm; (g) b = 0.00 mm; (h) b = 0.10 mm; (i) b = 0.20 mm
Figure 2. Normalized light intensity distribution in the x-direction of an Airyprime beam after different Airy transformation: (a) b = –0.50 mm; (b) b = –0.45 mm; (c) b = –0.40 mm; (d) b = –0.30 mm; (e) b = –0.20 mm; (f) b = –0.10 mm; (g) b = 0.00 mm; (h) b = 0.10 mm; (i) b = 0.20 mm.
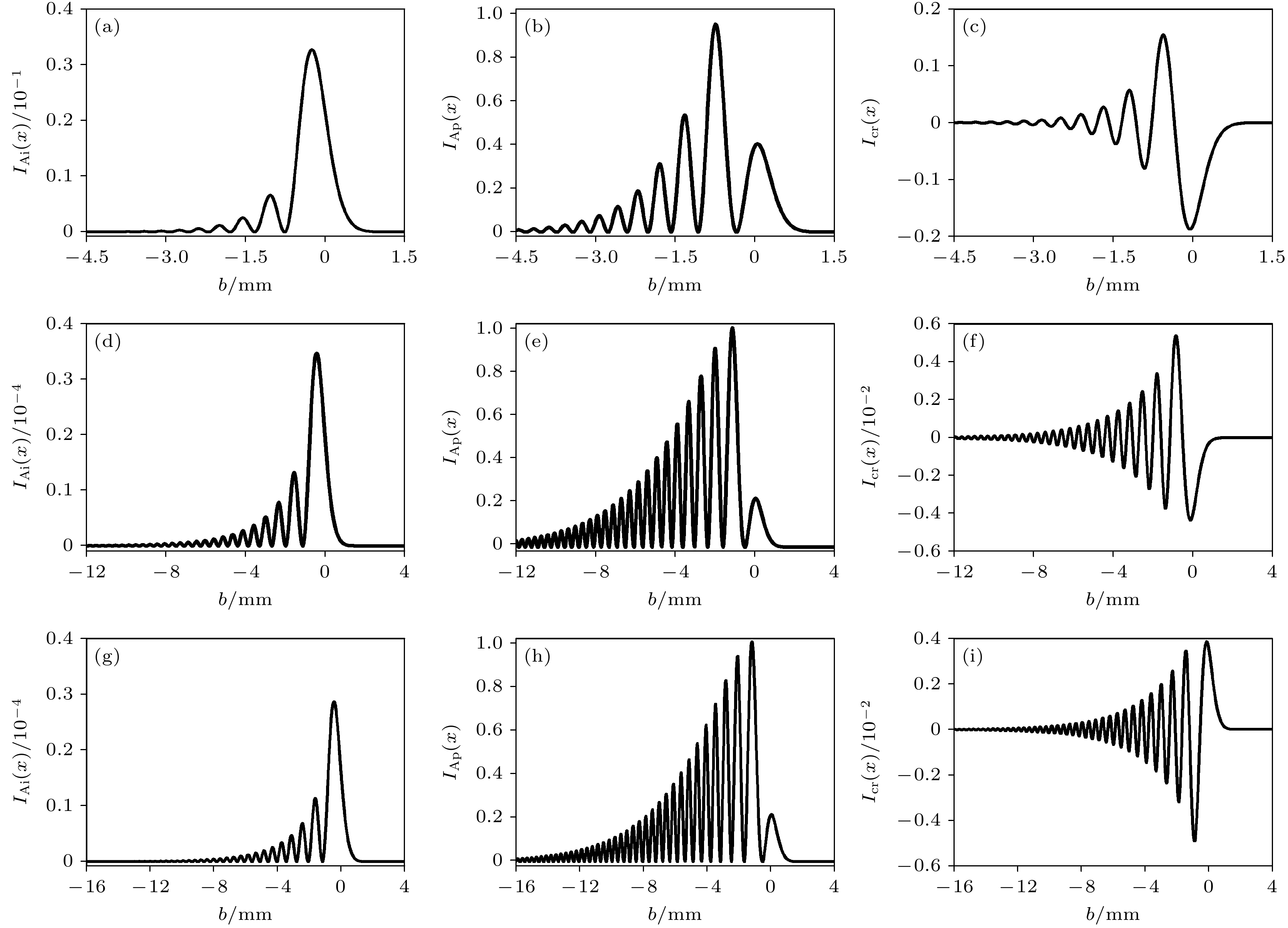
图 3 偏心艾里光束、偏心一阶艾里导数光束和交叉项在x方向上的光强分布 (a)—(c) b = –0.45 mm; (d)—(f) b = –0.20 mm; (g)—(i) b = 0.20 mm
Figure 3. Light intensity distribution in the x–direction of the eccentric Airy beam, the eccentric Airyprime beam, and the cross term: (a)—(c) b = –0.45 mm; (d)—(f) b = –0.20 mm; (g)—(i) b = 0.20 mm.
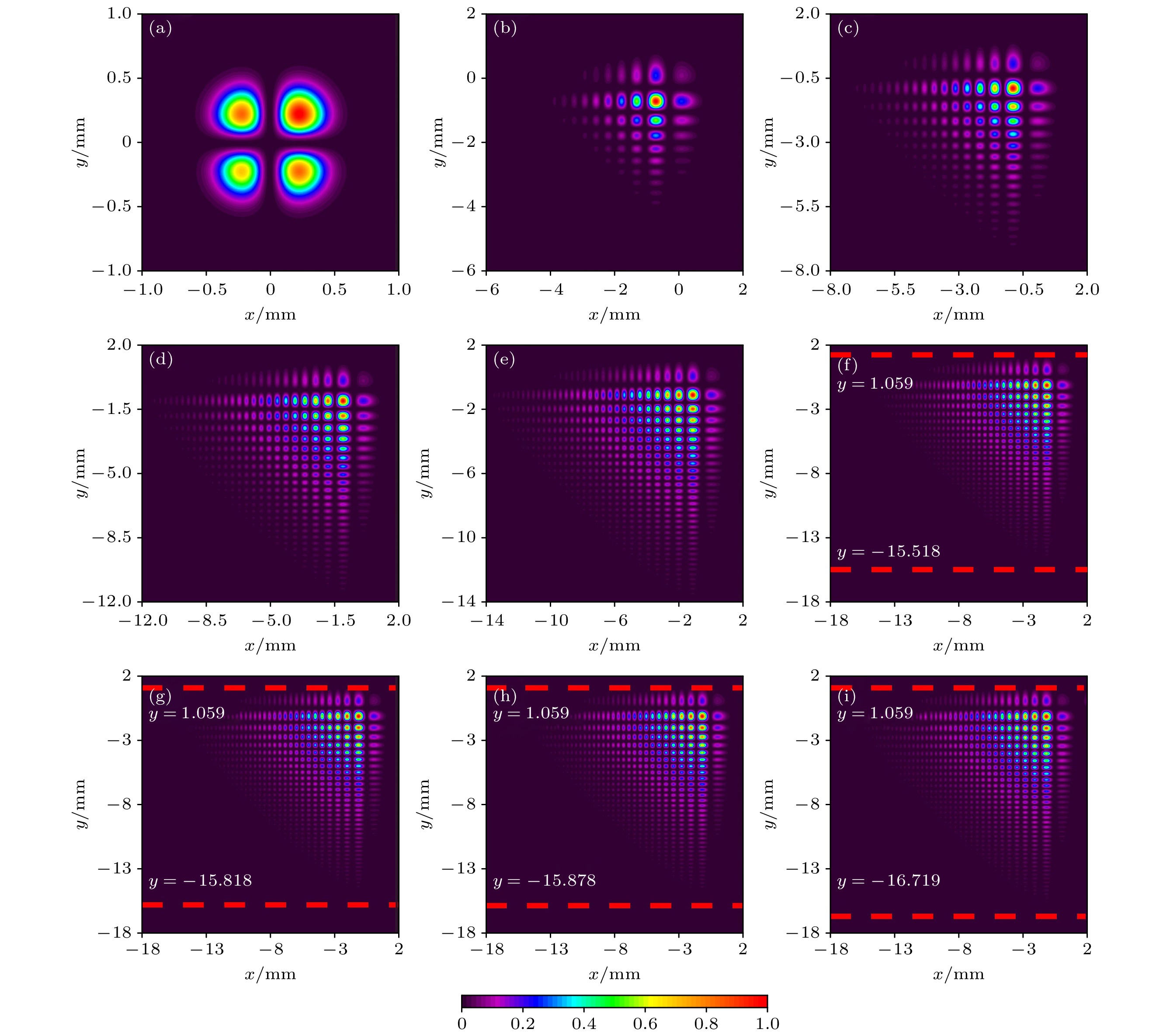
图 4 一阶艾里导数光束经不同艾里变换后的二维归一化光强分布 (a) b = c = –0.50 mm; (b) b = c = –0.45 mm; (c) b = c = –0.40 mm; (d) b = c = –0.30 mm; (e) b = c = –0.20 mm; (f) b = c = –0.10 mm; (g) b = c = 0.00 mm; (h) b = c = 0.10 mm; (i) b = c = 0.20 mm
Figure 4. Two-dimensional normalized intensity distribution of an Airyprime beam after different Airy transformation: (a) b = c = –0.50 mm; (b) b = c = –0.45 mm; (c) b = c = –0.40 mm; (d) b = c = –0.30 mm; (e) b = c = –0.20 mm; (f) b = c = –0.10 mm; (g) b = c = 0.00 mm; (h) b = c = 0.10 mm; (i) b = c = 0.20 mm.
图 5 艾里系数b对一阶艾里导数光束经艾里变换后x方向上的质心(a)和光束半宽(b)的影响
Figure 5. Effect of the Airy coefficient b on the centroid (a) and the beam half width (b) in the x-direction of an Airyprime beam after Airy transformation.
图 6 一阶艾里导数光束艾里变换的实验装置示意图
Figure 6. Experimental setup of the Airy transformation of an Airyprime beam.
图 7 (a) 用于产生一阶艾里导数光束的相位光栅; (b) 上传到SLM2的立方相位图
Figure 7. (a) Phase grating for generation of an Airyprime beam; (b) cubic phase pattern uploaded onto SLM2.
图 8 一阶艾里导数光束经不同艾里变换后二维光强分布的实验记录 (a) b = c = –0.50 mm; (b) b = c = –0.45 mm; (c) b = c = –0.40 mm; (d) b = c = –0.30 mm; (e) b = c = –0.20 mm; (f) b = c = –0.10 mm; (g) b = c = 0.00 mm; (h) b = c = 0.10 mm; (i) b = c = 0.20 mm
Figure 8. Experimental record of two-dimensional intensity profile of an Airyprime beam after different Airy transformation: (a) b = c = –0.50 mm; (b) b = c = –0.45 mm; (c) b = c = –0.40 mm; (d) b = c = –0.30 mm; (e) b = c = –0.20 mm; (f) b = c = –0.10 mm; (g) b = c = 0.00 mm; (h) b = c = 0.10 mm; (i) b = c = 0.20 mm.
图 9 艾里系数b对一阶艾里导数光束经艾里变换后x方向上的质心(a)和光束半宽(b)影响的实验测量
Figure 9. Experimental measurement of the effect of the Airy coefficient b on the centroid (a) and the beam half width (b) in the x-direction of an Airyprime beam after Airy transformation.
-
[1] Zang X, Dan W S, Zhou Y M, Lv H, Wang F, Cai Y J, Zhou G Q 2022 Opt. Express 30 3804
Google Scholar
[2] Kumari A, Dev V, Pal V 2024 Opt. Laser Technol. 168 109387
[3] Yu J, Wang Y P, Bai Z Y, Wu L P, Fu C L, Liu S, Liu Y 2023 Opt. Express 31 11053
Google Scholar
[4] Yu J, Tong S D, Long H H, Bai Z Y, Wu L P, Liu Y 2024 Opt. Express 32 6178
Google Scholar
[5] Dan W S, Zang X, Wang F, Zhou Y M, Xu Y Q, Chen R P, Zhou G Q 2022 Opt. Express 30 32704
Google Scholar
[6] Chen Z, Peng S Y, Zhang Z H, Liu J L, Meng Yang 2024 Opt. Lett. 49 6453
Google Scholar
[7] Chen D H, Mo Z W, Liang Z H, Jiang J J, Tang H L, Sun Y D, Wang Z Y, Wei Q F, Chen Y R, Deng D M 2024 Opt. Commun. 554 130109
Google Scholar
[8] Zhao S K, Li J C, Li T Q, Huang X W, Bai Y F, Fu X Q 2024 Laser Phys. 34 095001
Google Scholar
[9] Zhao S K, Huang X W, Bai Y F, Fu X Q 2024 Chaos, Solitons Fractals 187 115480
Google Scholar
[10] Zhou Y M, Zang X, Dan W S, Wang F, Chen R P, Zhou G Q 2023 Opt. Laser Technol. 162 109303
Google Scholar
[11] Zang X, Dan W S, Wang F, Zhou Y M, Cai Y J, Zhou G Q 2022 Opt. Lett. 47 5654
Google Scholar
[12] Zang X, Dan W S, Zhou Y M, Wang F, Cai Y J, Zhou G Q 2023 Opt. Lett. 48 912
Google Scholar
[13] Wang W X, Mi Z W, Zhang L P, Wang B Y, Han K Z, Lei C X, Man Z S, Ge X L 2023 Opt. Commun. 549 129879
Google Scholar
[14] Yang S, Yu P X, Wu J W, Zhang X, Xu Z, Man Z S, Ge X L, Fu S G, Lei C X, Chen C D, Deng D M, Zhang L P 2023 Opt. Express 31 35685
Google Scholar
[15] Zhang L P, Yang S, Li S Y, Man Z S, Ge X L, Lei C X, He S, Zhang W F, Deng D M, Chen C D 2024 Chaos, Solitons Fractals 181 114506
Google Scholar
[16] He J, Dan W S, Zang X, Zhou Y M, Wang F, Cai Y J, Zhou G Q 2024 Opt. Laser Technol. 168 109932
Google Scholar
[17] Zang X, Wang F, Dan W S, Zhou Y, M Zhou G Q 2022 Opt. Laser Technol. 155 108398
Google Scholar
[18] Chen C D, Zhang L P, Yang S, Li S Y, Deng D M 2024 Opt. Lett. 49 268
[19] Zheng X Q, Yang Y Z, Liu Y J, Lin X J, Liang Z H, Liu J, Deng D M 2024 Opt. Lett. 49 4393
Google Scholar
[20] Jiang Y F, Huang K K, Lu X H 2012 Opt. Commun. 285 4840
Google Scholar
[21] Jiang Y F, Huang K K, Lu X H 2012 J. Opt. Soc. Am. A: 29 1412
Google Scholar
[22] Ez-zariy L, Boufalah F, Dalil-Essakali L, Belafhal A 2018 Optik 171 501
Google Scholar
[23] Yaalou M, El Halba E M, Hricha Z, Belafhal A 2019 Opt. Quantum Electron. 51 64
Google Scholar
[24] Yaalou M, Hricha Z, El Halba E M, Belafhal A 2019 Opt. Quantum Electron. 51 308
Google Scholar
[25] Yaalou M, Hricha Z, Lazrek M, Belafhal A 2020 J. Mod. Opt. 67 771
Google Scholar
[26] Yaalou M, Hricha Z, Belafhal A 2020 Opt. Quantum Electron. 52 165
Google Scholar
[27] Yaalou M, Hricha Z, Belafhal A 2020 Opt. Quantum Electron. 52 461
Google Scholar
[28] Chu X C, Liu R J, Wang X, Han Z X, Ni Y H 2021 Opt. Appl. 51 473
[29] Zhang Q, Liu Z R, Wang X 2022 Results Phys. 35 105389
Google Scholar
[30] Huang H Q, Wu Y, Lin Z J, Xu D L, Jiang J J, Mo Z W, Yang H B, Deng D M 2022 Waves Random Complex Medium DOI10.1080/17455030.2022. 2066222
[31] Zhang Q, Liu Z R, Wang X 2022 Phys. Scr. 97 115502
Google Scholar
[32] Zhang Q, Liu Z R, Wang X 2022 Optik 251 168477
Google Scholar
[33] Tang H L, Fan Z J, Ouyang S G, Mo Z W, Xu D L, Huang H Y, Deng D M 2023 Results Phys. 50 106552
Google Scholar
[34] Lin Q D, Zhang H, Hu Z Q, Lu X, Lu X Y, Cai Y J, Zhao C L 2023 Photonics 10 974
Google Scholar
[35] Yaalou M, Hricha Z, Belafhal A 2023 Opt. Quantum Electron. 55 875
Google Scholar
[36] Yaalou M, Hricha Z, Belafhal A 2023 Opt. Quantum Electron. 55 138
Google Scholar
[37] Gradshteyn I S, Ryzhik I M 1980 Table of integrals, series, and products (New York: Academic Press
[38] Vallée O, Manuel S 2010 Airy Functions and Applications to Physics (London: Imperial College Press).
[39] Martínez-Herrero R, Mejías P M 1993 Opt. Lett. 18 1669
Google Scholar
[40] Nemes G, Serna J 1998 OSA TOPS 17 200
[41] Mei Z R, Zhao D M 2005 Appl. Opt. 44 1381
Google Scholar
[42] Deng D M 2005 Phys. Lett. A 341 352
Google Scholar
[43] 刘飞, 季小玲 2011 60 014216
Google Scholar
Liu F, Ji X L 2011 Acta Phys. Sin. 60 014216
Google Scholar
[44] 余佳益, 陈亚红, 蔡阳健 2016 65 214202
Google Scholar
Yu J Y, Chen Y H, Cai Y J 2016 Acta Phys. Sin. 65 214202
Google Scholar
[45] Mihoubi K, Bencheikh A, Manallah A 2018 Opt. Laser. Technol. 9 191
DownLoad:
Metrics
- Abstract views: 220
- PDF Downloads: 15
- Cited By: 0
