-
Understanding the phase stability and transformation kinetics of multi-principal element alloys (MPEAs) under extreme conditions is critical for optimizing their performance under extreme conditions such as high-temperature and high-pressure environment. In this work the high pressure-temperature (p-T) phase diagram and solid-liquid transition mechanism of an equiatomic NiCoCr alloy are investigated based on embedded atom method (EAM) potential, through advanced molecular dynamics (MD) simulation combined with enhanced sampling techniques. In order to overcome the timescale limitations of traditional MD in capturing phase transitions as rare events, a hybrid approach integrating well-tempered metadynamics (WTMetaD) and the on-the-fly probability-enhanced sampling with expanded ensembles is used in this work. Collective variables such as enthalpy per atom SH, and two-body entropy SS are used to explore the polymorphic states of the NiCoCr alloy. The crystallinity senv, potential energy U, and volume V are utilized to drive phase transitions, and sampling configurations are performed in the range of 1550–1750 K and 0–10 GPa by using multithermal-multibaric-multiumbrella simulation. Several key results about liquid-solid phase transition in NiCoCr alloy are obtained as follows. 1) Phase diagram prediction. NiCoCr alloy exhibits a stable body-centered cubic (BCC) phase under high-pressure condition (e.g. 10 GPa) at elevated temperatures (up to 1750 K), and a face-centered cubic stable (FCC) phase at room temperature and ambient pressure. The solid-liquid coexistence line shifts upward with the increase of pressure, raising the melting temperature from ~1400 K (ambient pressure) to about 1750 K (over 10 GPa). 2) Free energy landscape. The free energy curves corresponding to different thermodynamic conditions are obtained using reweighting techniques and block averaging methods, which reveal that the increase of pressure and decrease of temperature can reduce the free-energy difference ΔGL→BCC, while simultaneously increasing G*BCC→L required for melting. The combined effects of these changes enhance the stability of the BCC phase in NiCoCr under high-temperature and high-pressure condition. 3) Activation parameters and kinetic mechanism. For the activation parameters of solid-liquid dynamic mechanics, S*L→BCC of NiCoCr alloy decreases with the increase of temperature and the decrease of pressure ( from (–4.32±0.16) J·mol–1·K–1 at 1550 K to (–6.71±0.48) J·mol–1·K–1 at 1750 K, 0 GPa ), and |V*L→BCC| increases with temperature increasing and pressure decreasing ( from (–88.21±2.57) Å3 at 0 GPa to (–26.09±6.35) Å3 at 10 GPa, 1600 K). At constant temperature, increasing pressure lowers S* sensitivity to temperature change, whereas higher temperatures amplify pressure’s role in reducing |V*L→BCC|, the change of pressure has no significant effect on V*BCC→L. These results demonstrate that the synergistic effects of pressure and temperature on S* and V* dictate the phase stability and transformation kinetics of NiCoCr alloys under extreme conditions. The predicted p-T phase diagram and quantitative activation parameters provide critical ideas for designing MPEAs with tailored microstructures for high-pressure applications. Limitations of the EAM potential in describing magnetic interactions and non-equilibrium states are discussed, and the necessity of of future validation through first-principles calculations and high-pressure experiments is emphasized. 
-
Keywords:
- multi-principal elemental alloys /
- enhanced sampling /
- free energy /
- phase diagram /
- phase transition
-
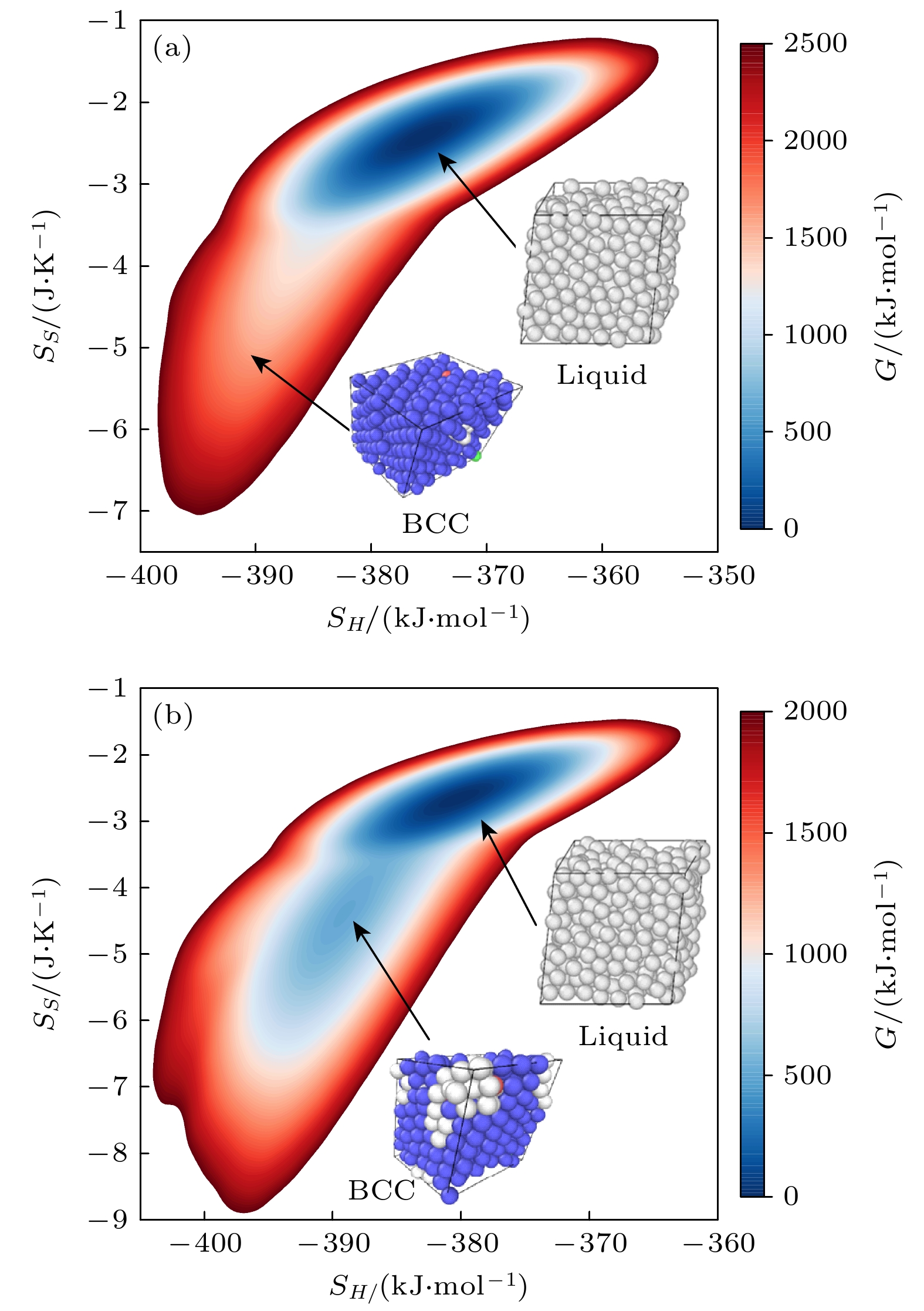
图 1 等原子比镍钴铬合金体系在高温常压下的二维吉布斯自由能面关于每原子焓(SH)和每原子两体熵(SS)的函数 (a) 1750 K和1 bar; (b) 1550 K和1 bar
Figure 1. 2D Gibbs free energy surface of the equiatomic NiCoCr alloy system at high temperature and atmospheric pressure, plotted as a function of the enthalpy per atom (SH) and two-body entropy per atom (SH): (a) 1750 K and 1 bar; (b) 1550 K and 1 bar.
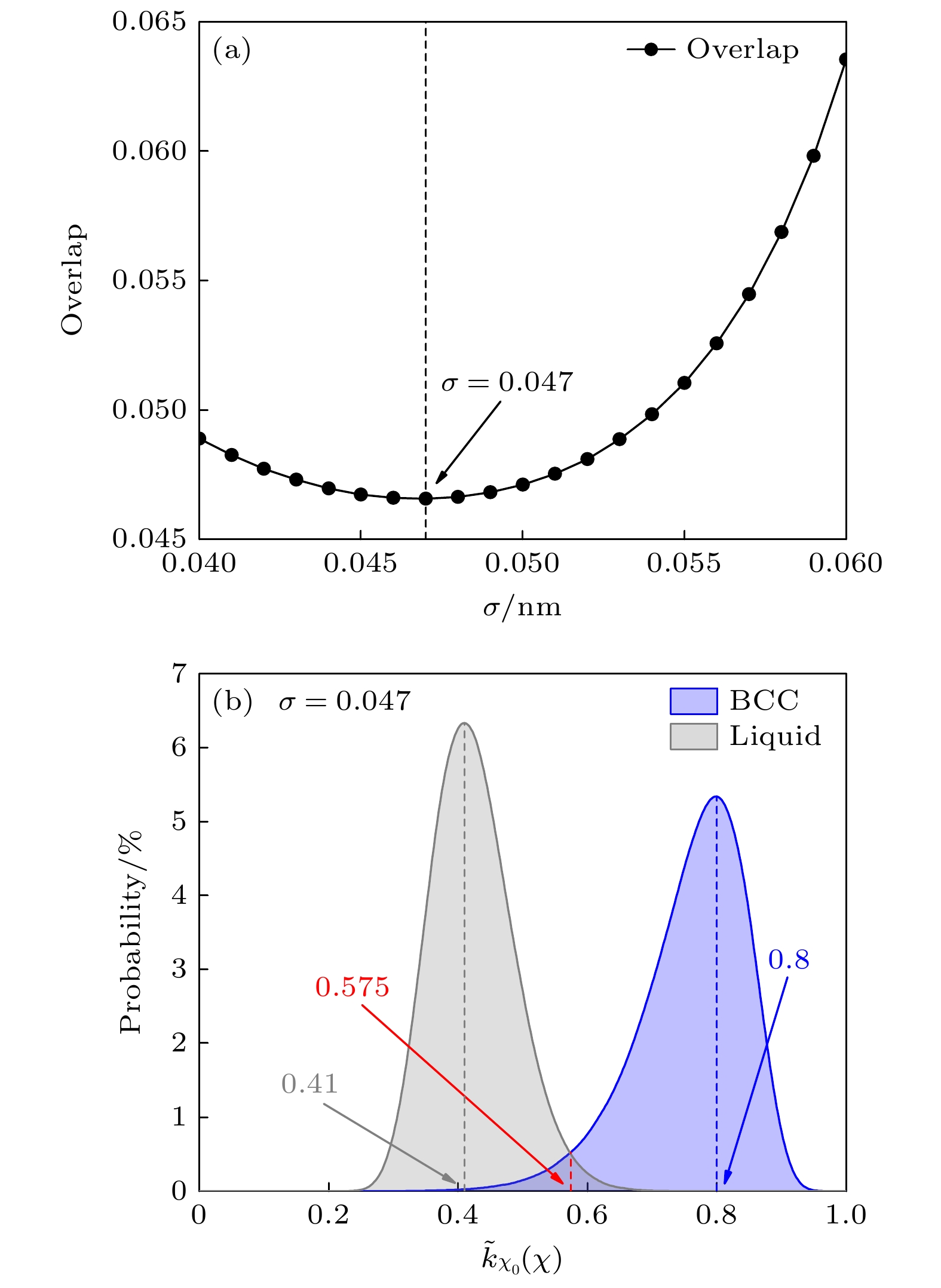
图 2 优化核函数最佳展宽参数 (a)基于最小重叠确定最佳展宽参数; (b)最佳展宽参数下(σ = 0.047), 镍钴铬合金体系液相与体心立方晶体相的核函数分布情况
Figure 2. The optimization of the kernel function’s optimal broadening parameter: (a) The optimal broadening parameter is determined by minimizing the overlap; (b) under the optimal broadening parameter (σ = 0.047), the distribution of the kernel functions for the liquid phase and body-centered cubic phase of the NiCoCr alloy system.
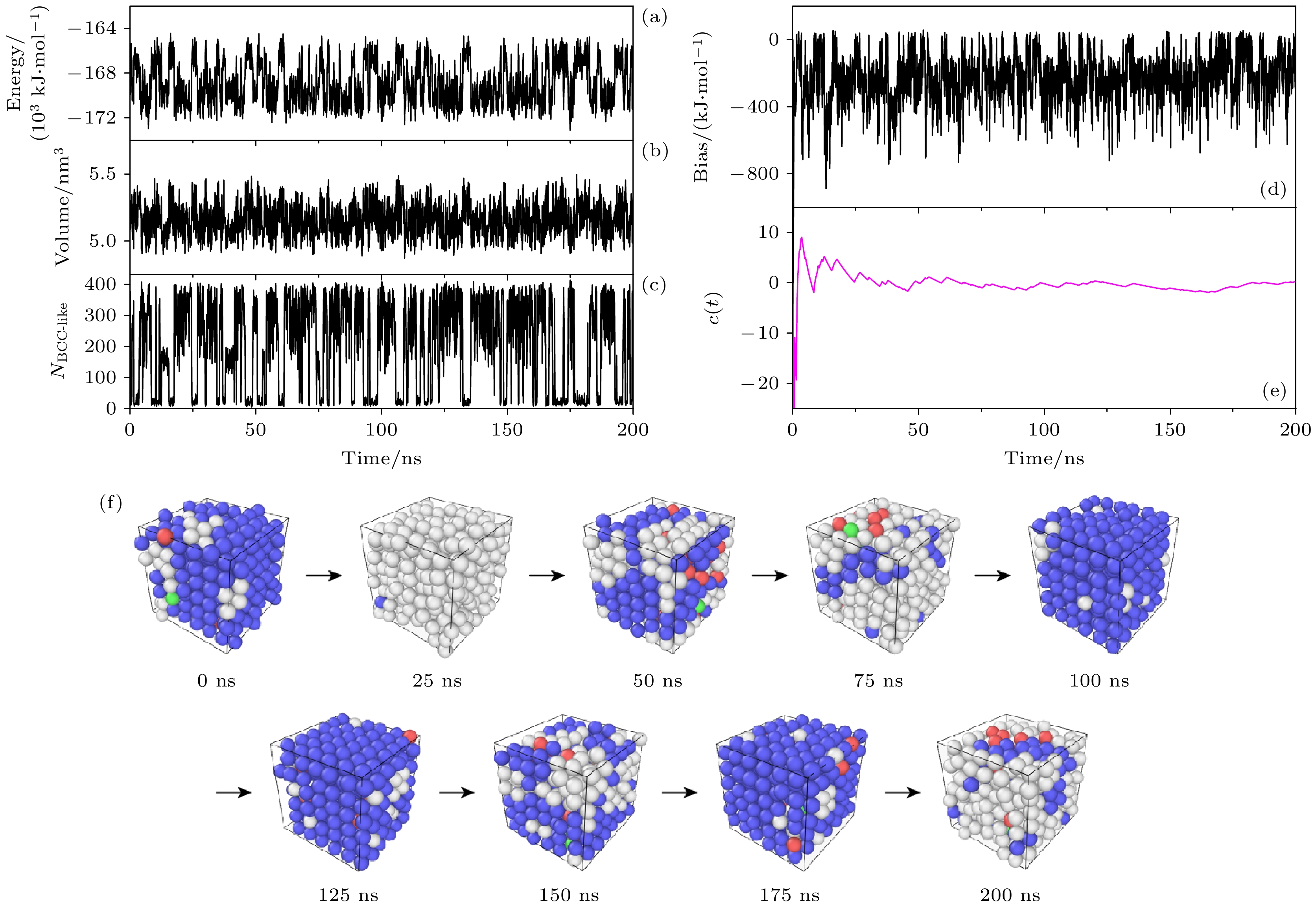
图 3 多温-多压-多伞增强采样中物理量及构型随时间的演化 (a)势能; (b)盒子体积; (c)类体心立方原子数; (d)偏置势; (e) c(t); (f)构型随时间的演化
Figure 3. Collective variables, bias, c(t) and configuration as a function of simulation time in the multithermal-multibaric-multiumbrella simulations: (a) Energy vs. time; (b) volume vs. time; (c) NBCC-like vs. time; (d) bias vs. time; (e) c(t) vs. time; (f) configuration vs. time.
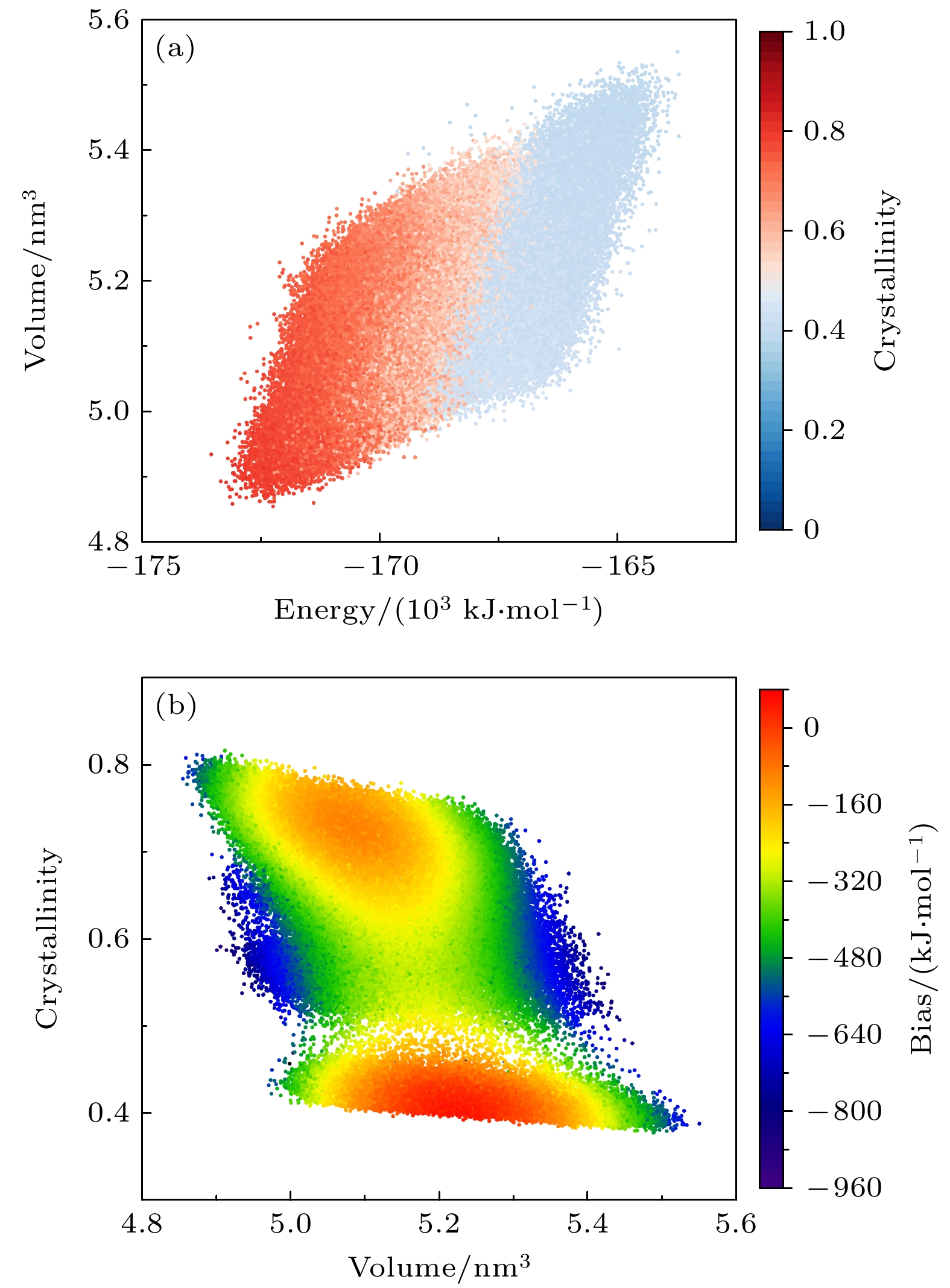
图 4 多温-多压-多伞模拟在NiCoCr构型空间中采样 (a) 结晶度在能量-体积空间中的分布; (b)偏置势随体积-结晶度的变化
Figure 4. Configuration space of NiCoCr sampled during the multithermal-multibaric-multiumbrella simulation: (a) The distribution of crystallinity in the energy-volume space; (b) the variation of the bias potential with respect to volume-crystallinity.
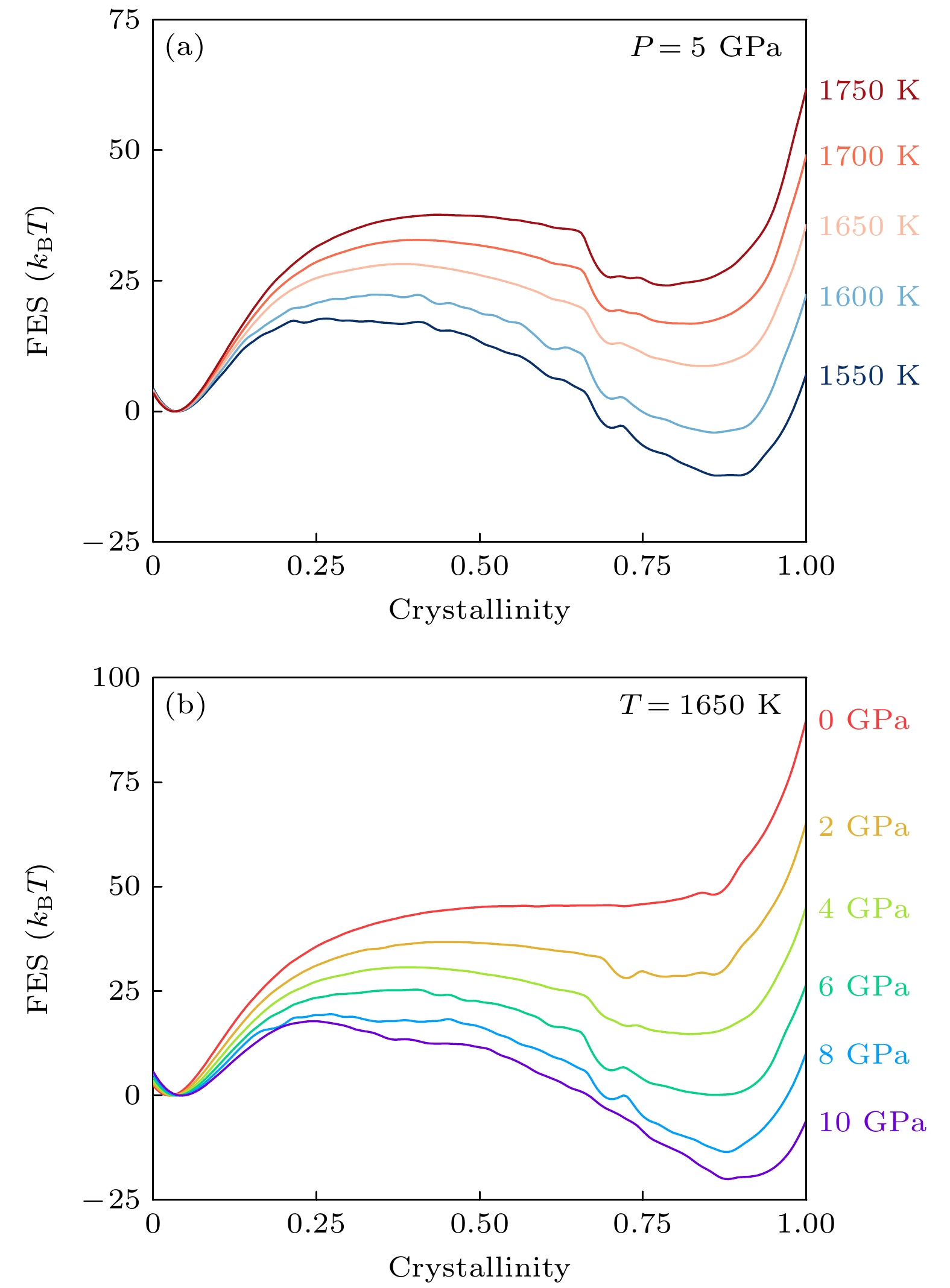
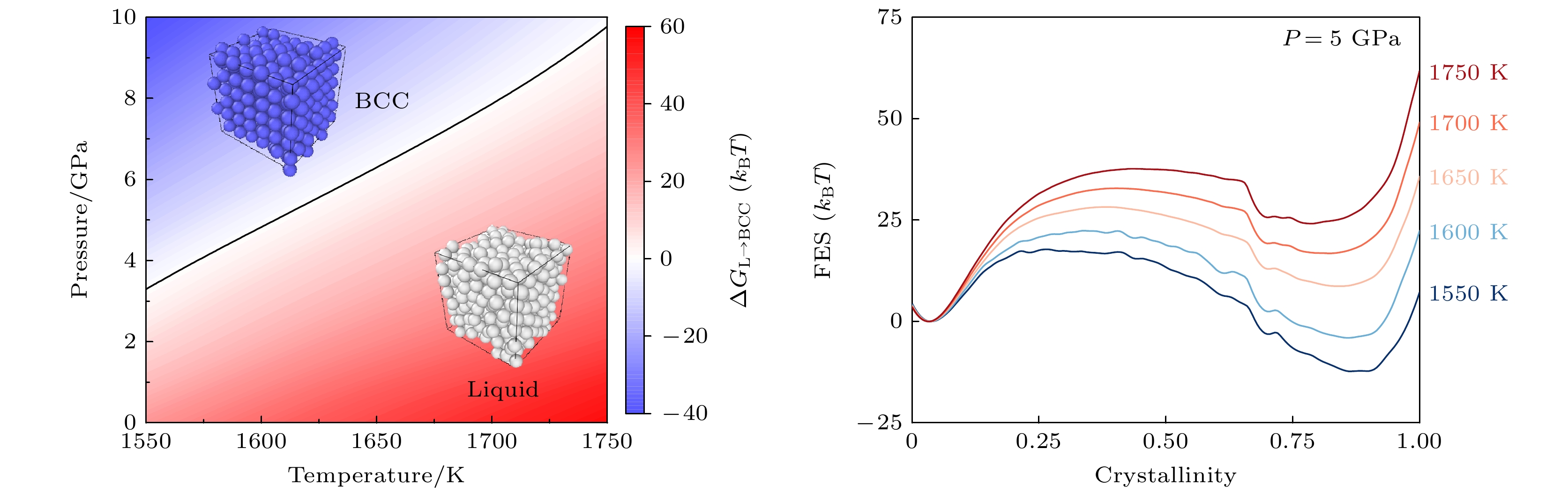
图 5 一维自由能曲线作为结晶度的函数 (a) 5 GPa下, 不同温度的自由能曲线; (b) 1650 K下, 不同压力的自由能曲线. 自由能误差约等于线宽
Figure 5. 1 D Free energy landscape as a function of crystallinity CV: (a) Free energy landscapecurves at different temperatures under 5 GPa; (b) free energy landscape curves under different pressures at 1650 K. Error bars are approximately equal to the linewidth.
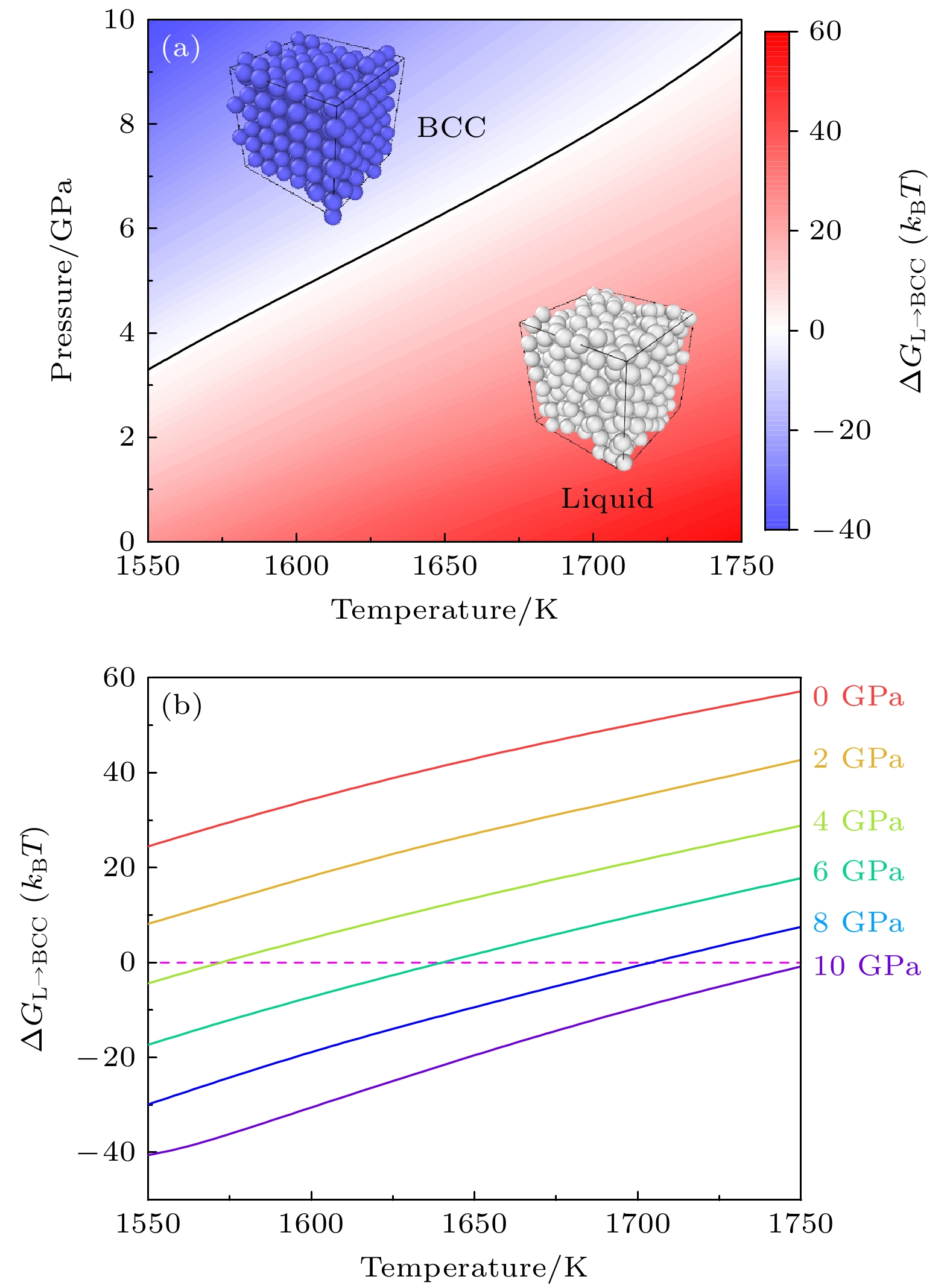
图 6 等原子比镍钴铬高温、高压相图的多温-多压-多伞模拟 (a)不同热力学条件下液相与体心立方相的自由能差ΔGL→BCC, 黑色实线表示固液共存线; (b)不同压力下液相与体心立方相的自由能差ΔGL→BCC随温度的变化
Figure 6. Phase digram of equiatomic NiCoCr sampled by the multithermal-multibaric-multiumbrella simulations: (a) The free energy difference between the Liquid and the BCC ΔGL→BCC under different thermodynamic conditions, the black solid line represents the solid-liquid coexistence line; (b) the change of the free energy difference ΔGL→BCC between liquid phase and BCC crystal at different pressures with increasing temperature.
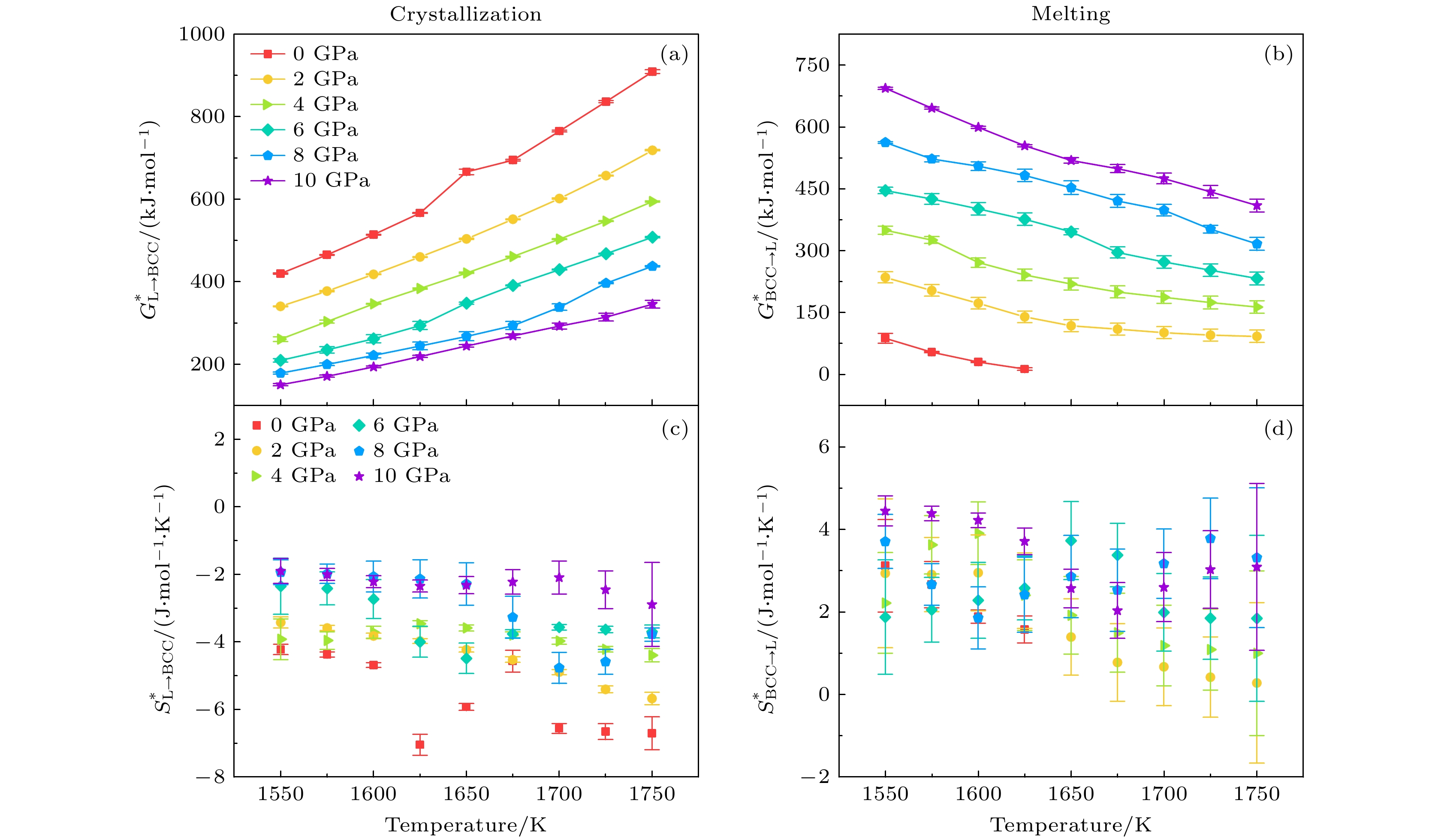
图 7 晶化和熔化过程中, 不同压力下激活自由能和激活熵随温度的变化 (a)晶化激活自由能G*L→BCC; (b)熔化激活自由能G*BCC→L; (c)晶化激活熵S*L→BCC; (d)熔化激活熵S*BCC→L
Figure 7. Activation free energy and activation entropy of crystallization and melting, as a function of temperature under different pressures: (a) The activation free energy G*L→BCC during crystallization; (b) the activation free energy G*BCC→L during melting; (c) the activation entropy S*L→BCC of crystallization process; (d) the activation entropy S*BCC→L of melting process.
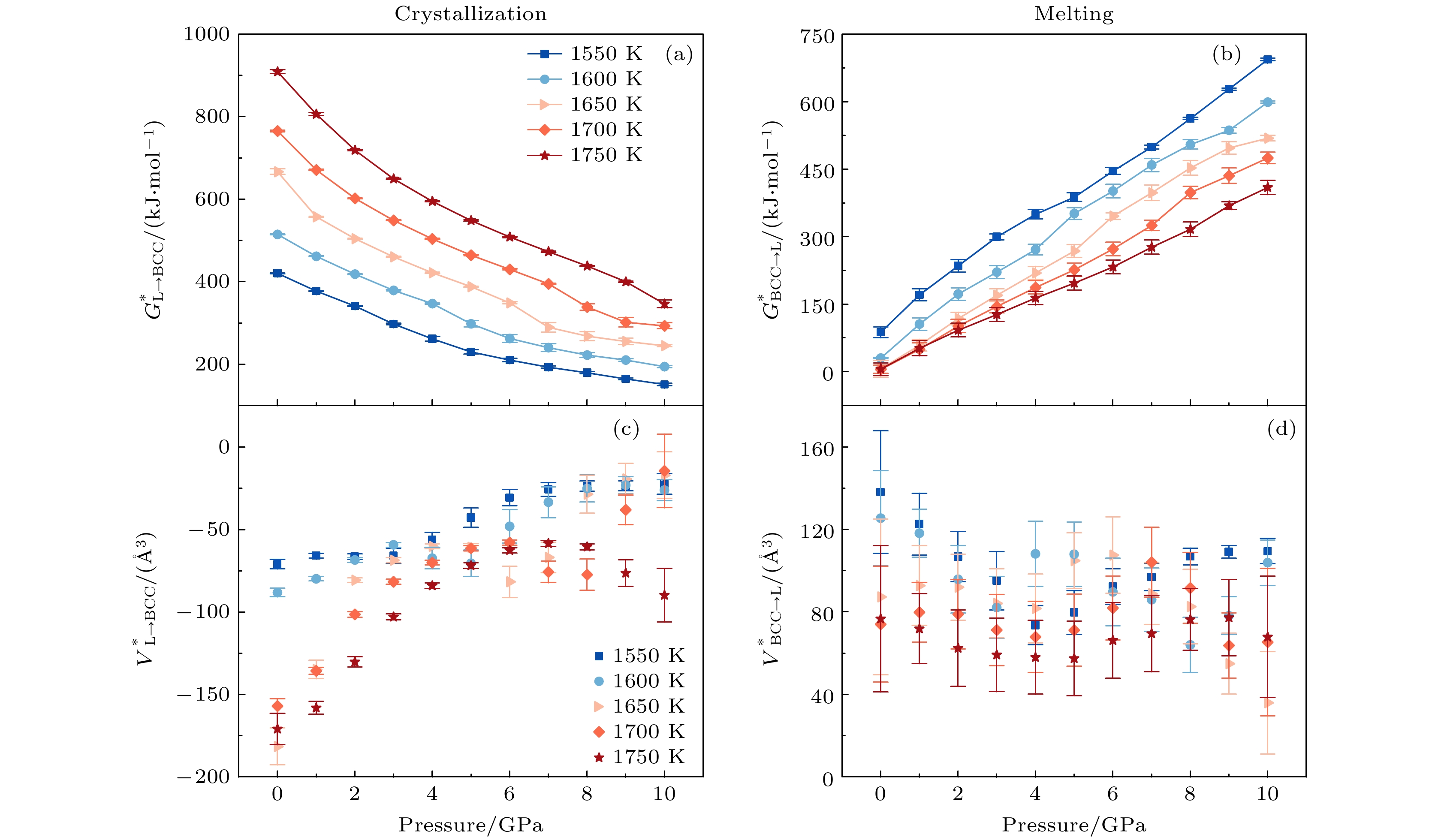
图 8 晶化和熔化过程中, 不同温度下激活自由能和激活体积随压力的变化 (a)晶化激活自由能G*L→BCC; (b)熔化激活自由能G*BCC→L; (c)晶化激活体积V*L→BCC; (d)熔化激活体积V*BCC→L
Figure 8. Activation free energy and activation volume of crystallization and melting, as a function of pressure under different temperatures: (a) The activation free energy G*L→BCC during crystallization; (b) the activation free energy G*BCC→L during melting; (c) the activation volume V*L→BCC of crystallization process; (d) the activation volume V*BCC→L of melting process
-
[1] Peng J, Chen B, Wang Z, Guo J, Wu B, Hao S, Zhang Q, Gu L, Zhou Q, Liu Z, Hong S, You S, Fu A, Shi Z, Xie H, Cao D, Lin C J, Fu G, Zheng L S, Jiang Y, Zheng N 2020 Nature 586 390
Google Scholar
[2] Du J, Jiang S, Cao P, Xu C, Wu Y, Chen H, Fu E, Lu Z 2023 Nat. Mater. 22 442
Google Scholar
[3] Bai X, Xie H, Zhang X, Zhao D, Rong X, Jin S, Liu E, Zhao N, He C 2024 Nat. Mater. 23 747
Google Scholar
[4] George E P, Curtin W A, Tasan C C 2020 Acta Mater. 188 435
Google Scholar
[5] Ma E, Wu X 2019 Nat. Commun. 10 5623
Google Scholar
[6] George E P, Raabe D, Ritchie R O 2019 Nat. Rev. Mater. 4 515
Google Scholar
[7] Yeh J W, Chen S K, Lin S J, Gan J Y, Chin T S, Shun T T, Tsau C H, Chang S Y 2004 Adv. Eng. Mater. 6 299
Google Scholar
[8] Hsu W L, Tsai C W, Yeh A C, Yeh J W 2024 Nat. Rev. Chem. 8 471
Google Scholar
[9] Wang M, Ma Z L, Xu Z Q, Cheng X W 2021 Scr. Mater. 191 131
Google Scholar
[10] Kumar N A P K, Li C, Leonard K J, Bei H, Zinkle S J 2016 Acta Mater. 113 230
Google Scholar
[11] Zhao S, He L xin, Fan X xia, Liu C hai, Long J ping, Wang L, Chang H, Wang J, Zhang W 2019 Surf. Coat. Technol. 375 215
Google Scholar
[12] Wu Z, Bei H, Pharr G M, George E P 2014 Acta Mater. 81 428
Google Scholar
[13] Gludovatz B, Hohenwarter A, Thurston K V S, Bei H, Wu Z, George E P, Ritchie R O 2016 Nat. Commun. 7 10602
Google Scholar
[14] Ding J, Yu Q, Asta M, Ritchie R O 2018 Proc. Natl. Acad. Sci. U. S. A. 115 8919
Google Scholar
[15] Smith T M, Kantzos C A, Zarkevich N A, Harder B J, Heczko M, Gradl P R, Thompson A C, Mills M J, Gabb T P, Lawson J W 2023 Nature 617 513
Google Scholar
[16] Panagiotopoulos A Z, Quirke N, Stapleton M, Tildesley D J 1988 Mol. Phys. 63 527
Google Scholar
[17] Frenkel D, Ladd A J C 1984 J. Chem. Phys. 81 3188
Google Scholar
[18] Grochola G 2004 J. Chem. Phys. 120 2122
Google Scholar
[19] Zhang L, Wang H, Car R, E W 2021 Phys. Rev. Lett. 126 236001
Google Scholar
[20] Kruglov I A, Yanilkin A, Oganov A R, Korotaev P 2019 Phys. Rev. B 100 174104
Google Scholar
[21] Chen T, Yuan F, Liu J, Geng H, Zhang L, Wang H, Chen M 2023 Phys. Rev. Mater. 7 053603
Google Scholar
[22] Pártay L B, Bartók A P, Csányi G 2010 J. Phys. Chem. B 114 10502
Google Scholar
[23] Dorrell J, Pártay L B 2020 J. Phys. Chem. B 124 6015
Google Scholar
[24] Marchant G A, Caro M A, Karasulu B, Pártay L B 2023 npj Comput. Mater. 9 131
Google Scholar
[25] Unglert N, Carrete J, Pártay L B, Madsen G K H 2023 Phys. Rev. Mater. 7 123804
Google Scholar
[26] Laio A, Parrinello M 2002 Proc. Natl. Acad. Sci. U. S. A. 99 12562
Google Scholar
[27] Barducci A, Bussi G, Parrinello M 2008 Phys. Rev. Lett. 100 020603
Google Scholar
[28] Valsson O, Parrinello M 2014 Phys. Rev. Lett. 113 090601
Google Scholar
[29] Dama J F, Rotskoff G, Parrinello M, Voth G A 2014 J. Chem. Theory Comput. 10 3626
Google Scholar
[30] Piaggi P M, Parrinello M 2019 Phys. Rev. Lett. 122 050601
Google Scholar
[31] Piaggi P M, Parrinello M 2019 J. Chem. Phys 150 244119
Google Scholar
[32] Piaggi P M, Valsson O, Parrinello M 2017 Phys. Rev. Lett. 119 015701
Google Scholar
[33] Invernizzi M, Valsson O, Parrinello M 2017 Proc. Natl. Acad. Sci. U. S. A. 114 3370
Google Scholar
[34] Piaggi P M, Parrinello M 2018 Proc. Natl. Acad. Sci. U. S. A. 115 10251
Google Scholar
[35] Oganov A R, Pickard C J, Zhu Q, Needs R J 2019 Nat. Rev. Mater. 4 331
Google Scholar
[36] Niu H, Bonati L, Piaggi P M, Parrinello M 2020 Nat. Commun. 11 2654
Google Scholar
[37] Invernizzi M, Piaggi P M, Parrinello M 2020 Phys. Rev. X 10 041034
[38] Tribello G A, Bonomi M, Branduardi D, Camilloni C, Bussi G 2014 Comput. Phys. Commun. 185 604
Google Scholar
[39] Li Q J, Sheng H, Ma E 2019 Nat. Commun. 10 3563
Google Scholar
[40] Dai S C, Yang Y, Wang Y J 2024 Phys. Rev. Mater. 8 033607
Google Scholar
[41] Cao F H, Wang Y J, Dai L H 2020 Acta Mater. 194 283
Google Scholar
[42] Bussi G, Donadio D, Parrinello M 2007 J. Chem. Phys. 126 014101
Google Scholar
[43] Parrinello M, Rahman A 1981 J. Appl. Phys. 52 7182
Google Scholar
[44] Flyvbjerg H, Petersen H G 1989 J. Chem. Phys. 91 461
Google Scholar
[45] Rein Ten Wolde P, Ruiz-Montero M J, Frenkel D 1996 J. Chem. Phys. 104 9932
Google Scholar
[46] Du J P, Yu P, Shinzato S, Meng F S, Sato Y, Li Y, Fan Y, Ogata S 2022 Acta Mater. 240 118314
Google Scholar
[47] Oganov A R, Glass C W 2006 J. Chem. Phys. 124 244704
Google Scholar
[48] Gusev V V, Adamson D, Deligkas A, Antypov D, Collins C M, Krysta P, Potapov I, Darling G R, Dyer M S, Spirakis P, Rosseinsky M J 2023 Nature 619 68
Google Scholar
DownLoad:
Metrics
- Abstract views: 244
- PDF Downloads: 0
- Cited By: 0
