Ce-La-Th合金高压相变的第一性原理计算

王艳; 曹仟慧; 胡翠娥; 曾召益

doi:10.7498/aps.68.20182128

摘要

采用第一性原理计算对Ce_0.8La_0.1Th_0.1在高压下fcc-bct的结构相变、弹性性质及热力学性质进行了研究讨论. 通过对计算结果的分析, 发现了合金在压力下的相变规律, 压强升高到31.6 GPa附近时fcc相开始向bct相转变, 到34.9 GPa时bct相趋于稳定. 对弹性模量的计算结果从另一角度反映了结构相变的信息. 最后, 利用准谐德拜模型对两种结构的高温高压热力学性质进行了理论预测.

关键词:

Abstract

The lanthanide and actinide metals and alloys are of great interest in experimental and theoretical high-pressure research, because of the unique behavior of the f electrons under pressure and their delocalization and participation in bonding. Cerium (Ce) metal is the first lanthanide element with a 4f electron. It has a very complex phase diagram and displays intriguing physical and chemical properties. In addition, it is expected to be an excellent surrogate candidate for plutonium (Pu), one of the radioactive transuranic actinides with a 5f electron. The bulk properties and phase transformation characteristics of Ce-based alloys are similar to those of Pu and its compounds. Thus, the investigations of Ce-based alloys are necessary and can potentially advance the understanding of the behavior of Pu. In this work, the equation of state, phase transition, elastic and thermodynamic properties of Ce_0.8La_0.1Th_0.1 alloy at high pressure are investigated by using first-principles calculations based on the density-functional theory. The structural properties of the Ce_0.8La_0.1Th_0.1 alloy are in good agreement with the available experimental and theoretical data. The lattice constant a decreases with pressure increasing, while c shows an opposite variation. It is found that the lattice parameter c shows abnormal jump. And the critical volume is located at 20.1 Å³. The axial ratio jumps from a value of about $\sqrt 2 $ (corresponding to the fcc structure) to a higher value, which indicates that the fcc-bct transition occurs. And the corresponding transition pressure is located at ~31.6 GPa. When the pressure rises to 34.9 GPa, the bct structure displays a saturated c/a axial ratio close to about 1.67. The Young's modulus E, shear modulus G and the Debye temperature of the fcc phase tend to be " softened” around the phase transition pressure. The vibrational free energy is obtained by using the quasi-harmonic Debye model. And then the thermodynamic properties including the thermal equation of state, heat capacity and entropy under high pressure and high temperature are also predicted successfully. The results show that the heat capacity and entropy increase rapidly with temperature increasing, and decrease with pressure increasing. The high pressure can suppress part of the anharmonicity caused by temperature.

Keywords:

作者及机构信息

重庆师范大学物理与电子工程学院, 重庆　401331

通信作者: 曾召益, zhaoyizeng@126.com

基金项目: 国家自然科学基金(批准号: 11504035)、重庆市教委科学技术研究项目(批准号: KJ1703044, KJ1703062)和重庆市科技计划(批准号: cstc2018jcyiAX0820)资助的课题.

Authors and contacts

School of Physics and Electronic Engineering, Chongqing Normal University, Chongqing 401331, China

Corresponding author: Zeng Zhao-Yi, zhaoyizeng@126.com

Funds: Project supported by the National Natural Science Foundation of China (Grant No. 11504035), the Scientific and Technological Reseaech of Chongqing Municipal Education Commission, China (Grant Nos. KJ1703044, KJ1703062), and the Chongqing Science and Technology Project, China (Grant No. cstc2018jcyiAX0820).

文章全文 : translate this paragraph

参考文献

[1]	Bridgman P W 1927 Proc. Am. Acad.Arts Sci. 62 207 Google Scholar
[2]	Bridgman P W 1951 Proc. Am. Acad. Arts Sci. 79 149 Google Scholar
[3]	Bridgman P W 1954 Proc. Am. Acad. Arts Sci. 83 1
[4]	Lanson A W, Tang T Y 1949 Phys. Rev. 76 301 Google Scholar
[5]	潘昊, 胡晓棉, 吴子辉, 戴诚达, 吴强 2012 61 206401 Google Scholar Pan H, Hu X M, Wu Z H, Dai C D, Wu Q 2012 Acta Phys. Sin. 61 206401 Google Scholar
[6]	Hu C E, Zeng Z Y, Zhang L, Chen X T, Cai L C 2011 Physica B 406 669 Google Scholar
[7]	Lawson A C, Williams A, Wire M S 1988 J. Less-common Met. 142 177 Google Scholar
[8]	Lawrence J M, Thompson J D, Fisk Z, Smith J L, Batlogg B 1984 Phys. Rev. B 29 4017 Google Scholar
[9]	Drymiotis F, Singleton J, Harrison N, Lashley J C, Bangura A, Mielke C H, Balicas L, Fisk Z, Migliori A, Smith J L 2005 J. Phys.: Condens. Matter 17 L77 Google Scholar
[10]	Ruff J P C, Islam Z, Das R K, Nojiri H, Cooley J C, Mielke C H 2012 Phys. Rev. B 85 024104 Google Scholar
[11]	Hu C E, Zeng Z Y, Zhang L, Chen X R, Cai L C 2010 Solid State Commun. 150 2362 Google Scholar
[12]	Zeng Z Y, Hu C E, Li Z G, Zhang W, Cai L C 2015 J. Alloys Compd. 640 201 Google Scholar
[13]	Blanco M A, Francisco E, Luaña V 2004 Comput. Phys. Commun. 158 57 Google Scholar
[14]	Blanco M A, MartínPendás A, Francisco E, Recio J M, Franco R 1996 J. Mol. Struct.: Theochem 368 245 Google Scholar
[15]	Francisco E, Recio J M, Blanco M A, Pendás A M 1998 J. Phys. Chem. 102 1595 Google Scholar
[16]	Francisco E, Sanjurjo G, Blanco M A 2001 Phys. Rev. B 63 094107 Google Scholar
[17]	Flórez M, Recio J M, Francisco E, Blanco M A, Pendás A M 2002 Phys. Rev. B 66 144112 Google Scholar
[18]	邓世杰, 赵宇宏, 侯华, 文志勤, 韩培德 2017 66 146101 Google Scholar Deng S J, Zhao H Y, Hou H, Wen Z Q, Han P D 2017 Acta Phys. Sin. 66 146101 Google Scholar
[19]	Vohra Y K, Holzapfel W B 1993 High Pressure Res. 11 223 Google Scholar
[20]	Olsen J S, Gerward L, Benedict U, Itié J P 1985 Physica B+C (Amsterdam) 133 129 Google Scholar
[21]	Gu G, Vohra Y K, Winand J M, Spirlet J C 1995 Scr. Metall. Mater. 32 2081 Google Scholar
[22]	Svane A 1996 Phys. Rev. B 53 4275
[23]	Soderlind P, Eriksson O, Wills J M, Boring A M 1993 Phys. Rev. B 48 9306 Google Scholar
[24]	Koskenmaki D C, Gschneidner K A 1978 Handb. Phys. Chem. Rare Earths 1 337 Google Scholar
[25]	Gerward L, Olsen J S, Diffr P 1993 Powder Diffr. 8 127 Google Scholar
[26]	Decremps F, Antonangeli D, Amadon B, Schmerber G 2009 Phys. Rev. B 80 132103 Google Scholar
[27]	Lipp M J, Kono Y, Jenei Z, Cynn H, Aracne-Ruddle C, Park C, Kenney-Benson C, Evans W J 2013 J. Phys: Condens. Matter 25 34

施引文献

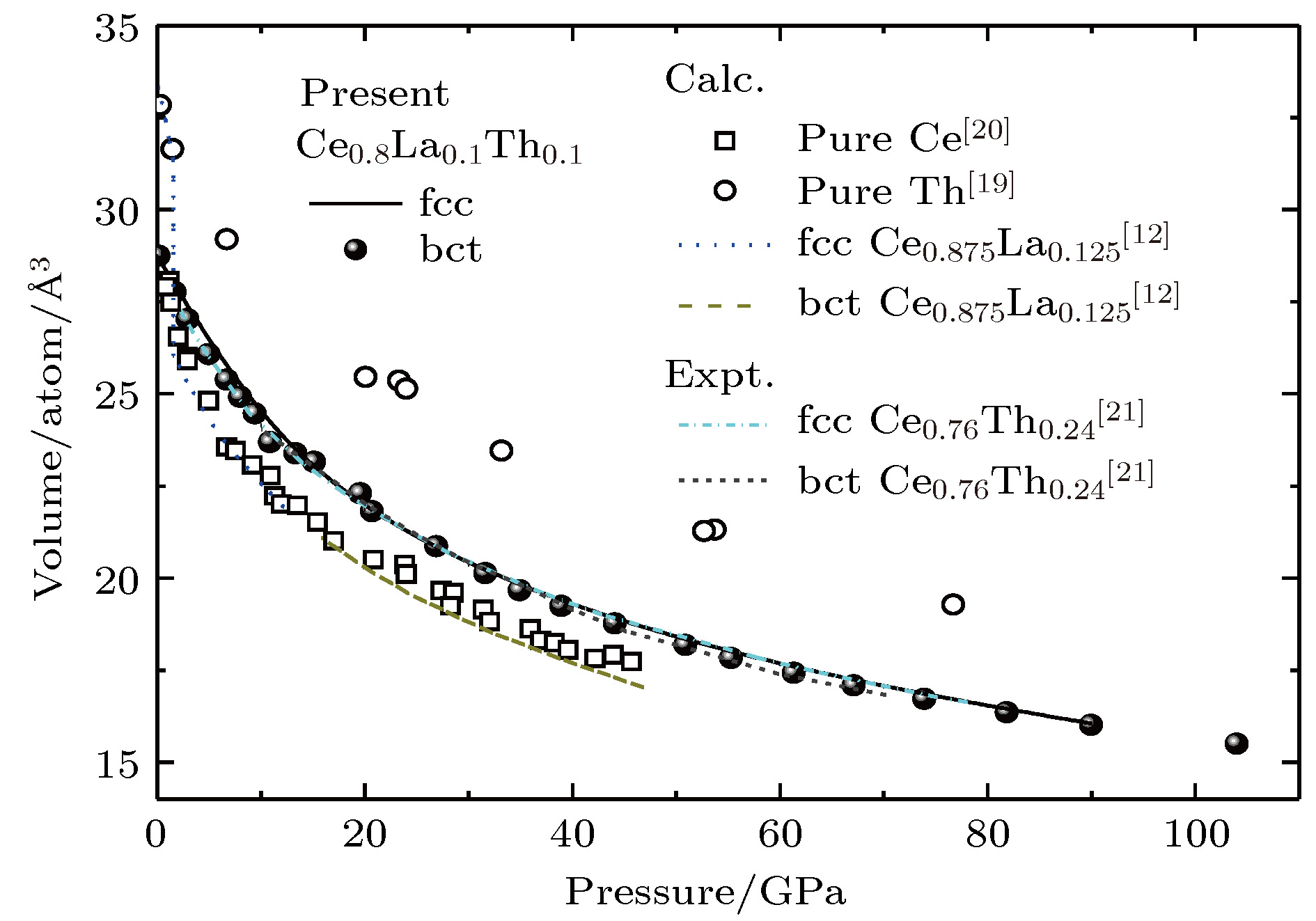
图 1 体积随压强变化的规律(黑色实点为直接加压结构优化后的结果, 黑色实线为状态方程拟合结果), 并与已有的Ce^[20], Th^[19], Ce_0.875La_0.125^[12]的计算值及Ce_0.76Th_0.24^[21]实验值进行比较

Fig. 1. The EOS of fcc and bct Ce-La-Th together with the experimental data (the black solid point is the result of the structure optimization, the black solid line is the fitting result of the EOS), together with the experimental data for Ce_0.76Th_0.24^[21] and the calculated results for Ce^[20], Th^[19], Ce_0.875La_0.125^[12].

下载: 全尺寸图片幻灯片

图 2 (a) 晶格参数随体积的变化关系; (b) 轴向比c/a随压强的变化关系, 并与已有的Ce_0.76Th_0.24^[21]实验结果和Ce_0.875La_0.125^[12]、纯Ce^[6]、纯Th^[11]计算结果进行比较

Fig. 2. (a) Lattice constants a and c of Ce_0.8La_0.1Th_0.1 as functions of volume; (b) the calculated axial ratio (c/a) of bct phase as functions of pressure.

下载: 全尺寸图片幻灯片

图 3 Ce-La-Th合金fcc相及bct相弹性常量随压强的变化

Fig. 3. Elastic constants as functions of pressure.

下载: 全尺寸图片幻灯片

图 4 剪切模量G、体模量B和杨氏模量E随压强的变化

Fig. 4. Shear modulus G, bulk modulus B and Young′s modulus E as functions of pressure.

下载: 全尺寸图片幻灯片

图 5 德拜温度随压强的变化

Fig. 5. The Debye temperature as a function of pressure.

下载: 全尺寸图片幻灯片

图 6 不同温度下的等温线, 其中V₀为零温零压下的体积, 小图为零压下体积随温度的变化

Fig. 6. Isotherms at different temperatures, where V₀ is the volume at zero temperature and zero pressure; the volumes at zero pressure as functions of temperature (the insert) .

下载: 全尺寸图片幻灯片

图 7 定容热容C_V随温度(a)和压强(b)的变化, 以及熵S随温度(c)和压强(d)的变化; 图中阴影区域包含fcc和bct两相的数据

Fig. 7. The constant volume heat capacity C_V versus temperature (a) and pressure (b), and the entropy S versus temperature (c) and pressure (d).

下载: 全尺寸图片幻灯片

表 1 零温零压下fcc相Ce-La-Th合金的平衡体积(V₀)及体积模量(B₀)

Table 1. Equilibrium volume (V₀) and bulk modulus (B₀) of Ce-La-Th of fcc phase at 0 GPa and 0 K.

V₀/Å³ B₀ / GPa

Present Ce_0.8La_0.1Th_0.1 28.91 35.96
Calc.^[12] Ce_0.875La_0.125 28.00 32.50
Calc. Pure Ce 27.07^[6], 24.7^[22] 41.72^[6], 48.4^[22], 37^[23]
Expt. Pure Ce 29.0^[20], 28.06^[24] 20^[20], 35.0^[25]

下载: 导出CSV

map

[1]	Bridgman P W 1927 Proc. Am. Acad.Arts Sci. 62 207 Google Scholar
[2]	Bridgman P W 1951 Proc. Am. Acad. Arts Sci. 79 149 Google Scholar
[3]	Bridgman P W 1954 Proc. Am. Acad. Arts Sci. 83 1
[4]	Lanson A W, Tang T Y 1949 Phys. Rev. 76 301 Google Scholar
[5]	潘昊, 胡晓棉, 吴子辉, 戴诚达, 吴强 2012 61 206401 Google Scholar Pan H, Hu X M, Wu Z H, Dai C D, Wu Q 2012 Acta Phys. Sin. 61 206401 Google Scholar
[6]	Hu C E, Zeng Z Y, Zhang L, Chen X T, Cai L C 2011 Physica B 406 669 Google Scholar
[7]	Lawson A C, Williams A, Wire M S 1988 J. Less-common Met. 142 177 Google Scholar
[8]	Lawrence J M, Thompson J D, Fisk Z, Smith J L, Batlogg B 1984 Phys. Rev. B 29 4017 Google Scholar
[9]	Drymiotis F, Singleton J, Harrison N, Lashley J C, Bangura A, Mielke C H, Balicas L, Fisk Z, Migliori A, Smith J L 2005 J. Phys.: Condens. Matter 17 L77 Google Scholar
[10]	Ruff J P C, Islam Z, Das R K, Nojiri H, Cooley J C, Mielke C H 2012 Phys. Rev. B 85 024104 Google Scholar
[11]	Hu C E, Zeng Z Y, Zhang L, Chen X R, Cai L C 2010 Solid State Commun. 150 2362 Google Scholar
[12]	Zeng Z Y, Hu C E, Li Z G, Zhang W, Cai L C 2015 J. Alloys Compd. 640 201 Google Scholar
[13]	Blanco M A, Francisco E, Luaña V 2004 Comput. Phys. Commun. 158 57 Google Scholar
[14]	Blanco M A, MartínPendás A, Francisco E, Recio J M, Franco R 1996 J. Mol. Struct.: Theochem 368 245 Google Scholar
[15]	Francisco E, Recio J M, Blanco M A, Pendás A M 1998 J. Phys. Chem. 102 1595 Google Scholar
[16]	Francisco E, Sanjurjo G, Blanco M A 2001 Phys. Rev. B 63 094107 Google Scholar
[17]	Flórez M, Recio J M, Francisco E, Blanco M A, Pendás A M 2002 Phys. Rev. B 66 144112 Google Scholar
[18]	邓世杰, 赵宇宏, 侯华, 文志勤, 韩培德 2017 66 146101 Google Scholar Deng S J, Zhao H Y, Hou H, Wen Z Q, Han P D 2017 Acta Phys. Sin. 66 146101 Google Scholar
[19]	Vohra Y K, Holzapfel W B 1993 High Pressure Res. 11 223 Google Scholar
[20]	Olsen J S, Gerward L, Benedict U, Itié J P 1985 Physica B+C (Amsterdam) 133 129 Google Scholar
[21]	Gu G, Vohra Y K, Winand J M, Spirlet J C 1995 Scr. Metall. Mater. 32 2081 Google Scholar
[22]	Svane A 1996 Phys. Rev. B 53 4275
[23]	Soderlind P, Eriksson O, Wills J M, Boring A M 1993 Phys. Rev. B 48 9306 Google Scholar
[24]	Koskenmaki D C, Gschneidner K A 1978 Handb. Phys. Chem. Rare Earths 1 337 Google Scholar
[25]	Gerward L, Olsen J S, Diffr P 1993 Powder Diffr. 8 127 Google Scholar
[26]	Decremps F, Antonangeli D, Amadon B, Schmerber G 2009 Phys. Rev. B 80 132103 Google Scholar
[27]	Lipp M J, Kono Y, Jenei Z, Cynn H, Aracne-Ruddle C, Park C, Kenney-Benson C, Evans W J 2013 J. Phys: Condens. Matter 25 34

[1]	田城, 蓝剑雄, 王苍龙, 翟鹏飞, 刘杰. BaF ₂高压相变行为的第一性原理研究. , 2022, 71(1): 017102. doi: 10.7498/aps.71.20211163
[2]	田城, 蓝剑雄, 王苍龙, 翟鹏飞, 刘杰. BaF2高压相变行为的第一性原理研究. , 2021, (): . doi: 10.7498/aps.70.20211163
[3]	李恬静, 操秀霞, 唐士惠, 何林, 孟川民. 蓝宝石冲击消光晶向效应的第一性原理. , 2020, 69(4): 046201. doi: 10.7498/aps.69.20190955
[4]	王春杰, 王月, 高春晓. 高压下纳米晶ZnS晶粒和晶界性质及相变机理. , 2020, 69(14): 147202. doi: 10.7498/aps.69.20200240
[5]	郭静, 吴奇, 孙力玲. 高压下的铁基超导体:现象与物理. , 2018, 67(20): 207409. doi: 10.7498/aps.67.20181651
[6]	董家君, 姚明光, 刘世杰, 刘冰冰. 高压下准一维纳米结构的研究. , 2017, 66(3): 039101. doi: 10.7498/aps.66.039101
[7]	刘博, 王煊军, 卜晓宇. 高压下NH4ClO4结构、电子及弹性性质的第一性原理研究. , 2016, 65(12): 126102. doi: 10.7498/aps.65.126102
[8]	唐士惠, 操秀霞, 何林, 祝文军. 空位缺陷和相变对冲击压缩下蓝宝石光学性质的影响. , 2016, 65(14): 146201. doi: 10.7498/aps.65.146201
[9]	王金荣, 朱俊, 郝彦军, 姬广富, 向钢, 邹洋春. 高压下RhB的相变、弹性性质、电子结构及硬度的第一性原理计算. , 2014, 63(18): 186401. doi: 10.7498/aps.63.186401
[10]	颜小珍, 邝小渝, 毛爱杰, 匡芳光, 王振华, 盛晓伟. 高压下ErNi2B2C弹性性质、电子结构和热力学性质的第一性原理研究. , 2013, 62(10): 107402. doi: 10.7498/aps.62.107402
[11]	王海燕, 历长云, 高洁, 胡前库, 米国发. 高压下TiAl3结构及热动力学性质的第一性原理研究. , 2013, 62(6): 068105. doi: 10.7498/aps.62.068105
[12]	张品亮, 龚自正, 姬广富, 刘崧. α-Ti2Zr高压物性的第一性原理计算研究. , 2013, 62(4): 046202. doi: 10.7498/aps.62.046202
[13]	周平, 王新强, 周木, 夏川茴, 史玲娜, 胡成华. 第一性原理研究硫化镉高压相变及其电子结构与弹性性质. , 2013, 62(8): 087104. doi: 10.7498/aps.62.087104
[14]	陈中钧. 高压下MgS的弹性性质、电子结构和光学性质的第一性原理研究. , 2012, 61(17): 177104. doi: 10.7498/aps.61.177104
[15]	余本海, 陈东. α-, β-和γ-Si3N4 高压下的电子结构和相变: 第一性原理研究. , 2012, 61(19): 197102. doi: 10.7498/aps.61.197102
[16]	明星, 王小兰, 杜菲, 陈岗, 王春忠, 尹建武. 菱铁矿FeCO3高压相变与性质的第一性原理研究. , 2012, 61(9): 097102. doi: 10.7498/aps.61.097102
[17]	邓杨, 王如志, 徐利春, 房慧, 严辉. 立方(Ba0.5Sr0.5)TiO3高压诱导带隙变化的第一性原理研究. , 2011, 60(11): 117309. doi: 10.7498/aps.60.117309
[18]	季正华, 曾祥华, 岑洁萍, 谭明秋. ZnSe相变、电子结构的第一性原理计算. , 2010, 59(2): 1219-1224. doi: 10.7498/aps.59.1219
[19]	孙博, 刘绍军, 祝文军. Fe在高压下第一性原理计算的芯态与价态划分. , 2006, 55(12): 6589-6594. doi: 10.7498/aps.55.6589
[20]	宫长伟, 王轶农, 杨大智. NiTi形状记忆合金马氏体相变的第一性原理研究. , 2006, 55(6): 2877-2881. doi: 10.7498/aps.55.2877

计量

文章访问数: 10620
PDF下载量: 133
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

Ce-La-Th合金高压相变的第一性原理计算