-
The mechanism of controlling single-photon scattering in a hybrid system consisting of superconducting qubits coupled to aSu-Schrieffer-Heeger (SSH) topological photonic lattice is investigated under the influence of an artificial gauge field. This research is driven by the growing interest in the intersection between quantum optics and condensed matter physics, particularly in the field of topological quantum optics, where the robustness of photon transport against defects and impurities can be used for quantum information processing. To achieve this, a theoretical model, which incorporates the phase of the artificial gauge field into the coupling between superconducting qubits and the SSH photonic lattice, is developed in this work. The analytical expressions for the reflection and transmission amplitudes of single photons are derived by using the probability-amplitude method. The results show that the artificial gauge field can effectively control single photon scattering in both the upper energy band and the lower energy band of the SSH lattice, thereby enabling total transmission in the upper band and total reflection in the lower band. This band-dependent scattering behavior exhibits a high degree of symmetry with respect to the lattice momentum and energy bands. Importantly, the reflection coefficient can be made independent of the lattice coupling strength and dependent solely on the topological properties of the lattice. This finding suggests a robust method of detecting topological invariants in photonic lattices. Furthermore, our analysis is extended to various coupling configurations between superconducting qubits and the photonic lattice, highlighting the versatility of the artificial gauge field in manipulating photon transport. These findings not only provide new insights into the control of photon transport in topological photonic lattices, but also open the door to the development of novel quantum optical devices and robust quantum information processing platforms.
-
Keywords:
- single-photon scattering /
- superconducting qubits /
- topology
-
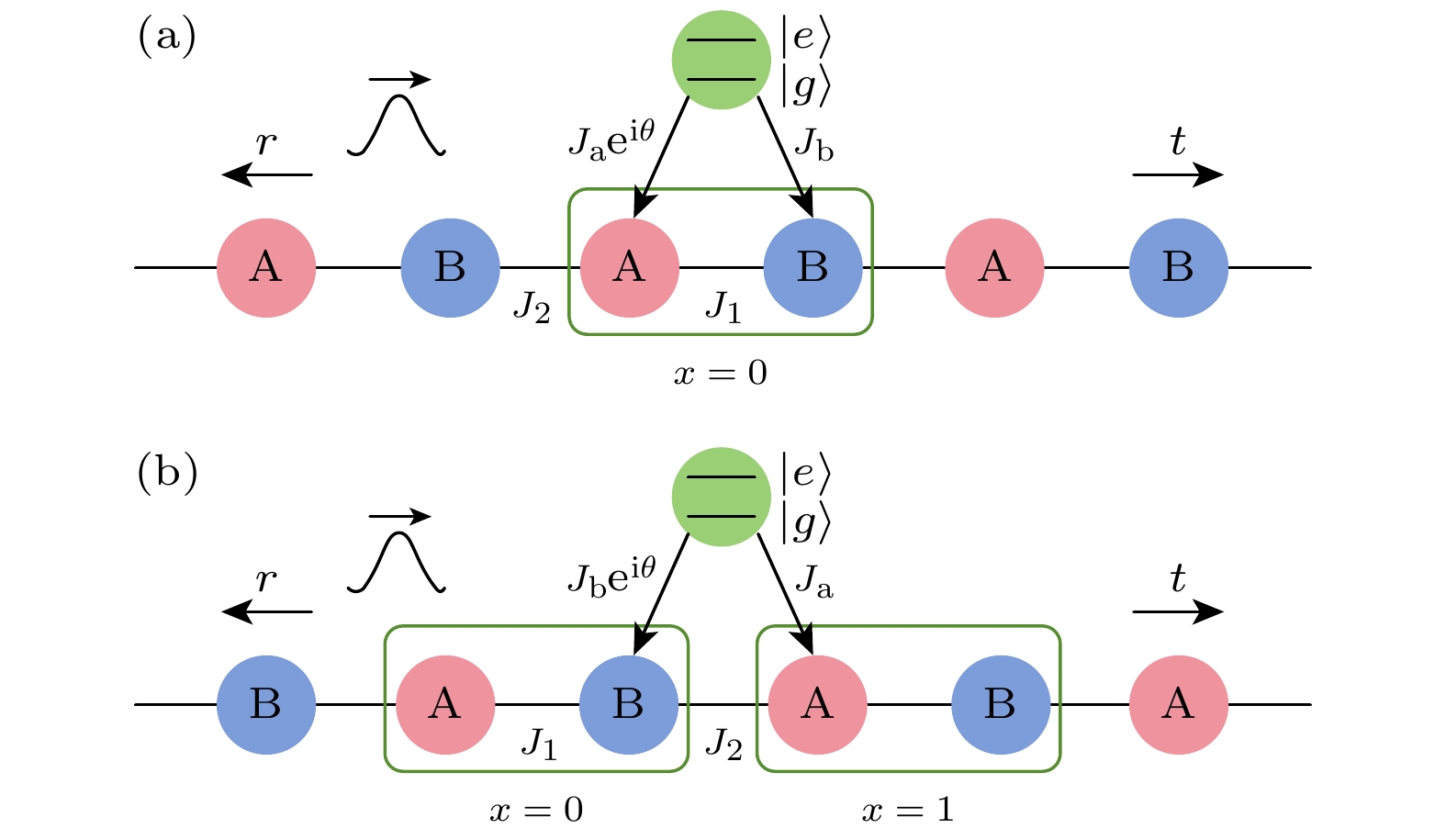
图 1 超导比特耦合到SSH拓扑光子晶格体系中的单光子相干输运示意图 (a)超导比特同时耦合到元胞内的两个格点; (b)超导比特同时耦合到元胞间的两个格点, $\theta $为外加人工规范场相位
Figure 1. Schematic illustration of single-photon coherent transport in a system of superconducting qubits coupled to an SSH topological photonic lattice system: (a) Superconducting qubit simultaneously coupled to two lattice sites within the same unit cell; (b) superconducting qubit simultaneously coupled to two lattice sites across different unit cells, $\theta $ is the phase of the applied artificial gauge field.
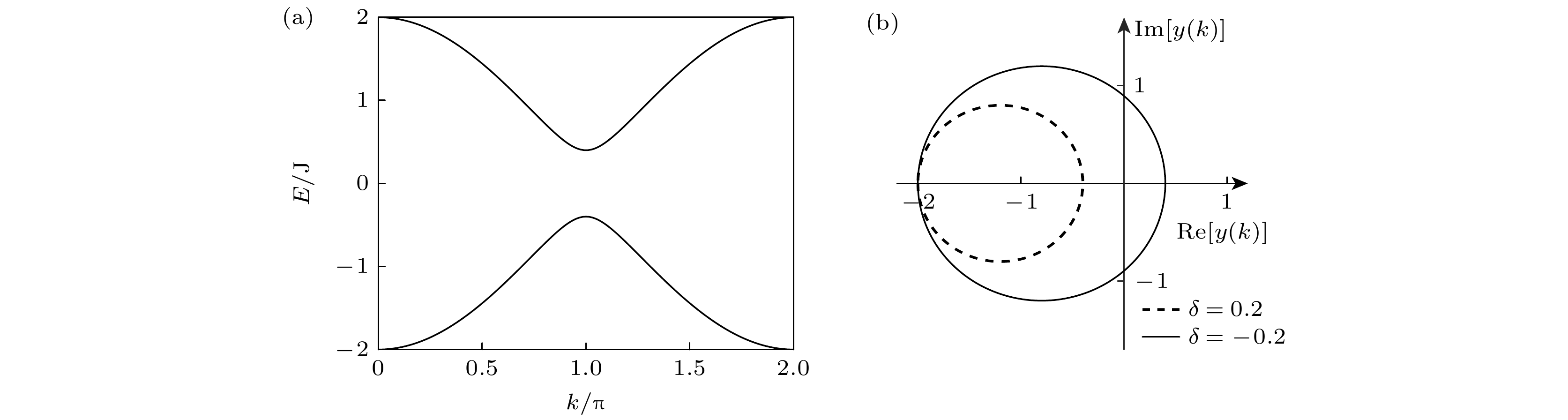
图 2 SSH 拓扑光子晶格的能带结构与拓扑特性 (a)能量$E$关于波矢$k$的示意图, 其他参数设定为$\delta = 0.2$, $J = 1$; (b) SSH光子晶格拓扑缠绕示意图, 其中$\delta = 0.2$和$\delta = - 0.2$
Figure 2. Energy band structure and topological properties of the SSH topological photonic lattice: (a) Schematic diagram of energy $E$ as a function of $k$. Other parameters are set to $\delta = 0.2$, $J = 1$; (b) schematic diagram of the SSH photonic lattice topological winding, for $\delta = 0.2$ and $\delta = - 0.2$.
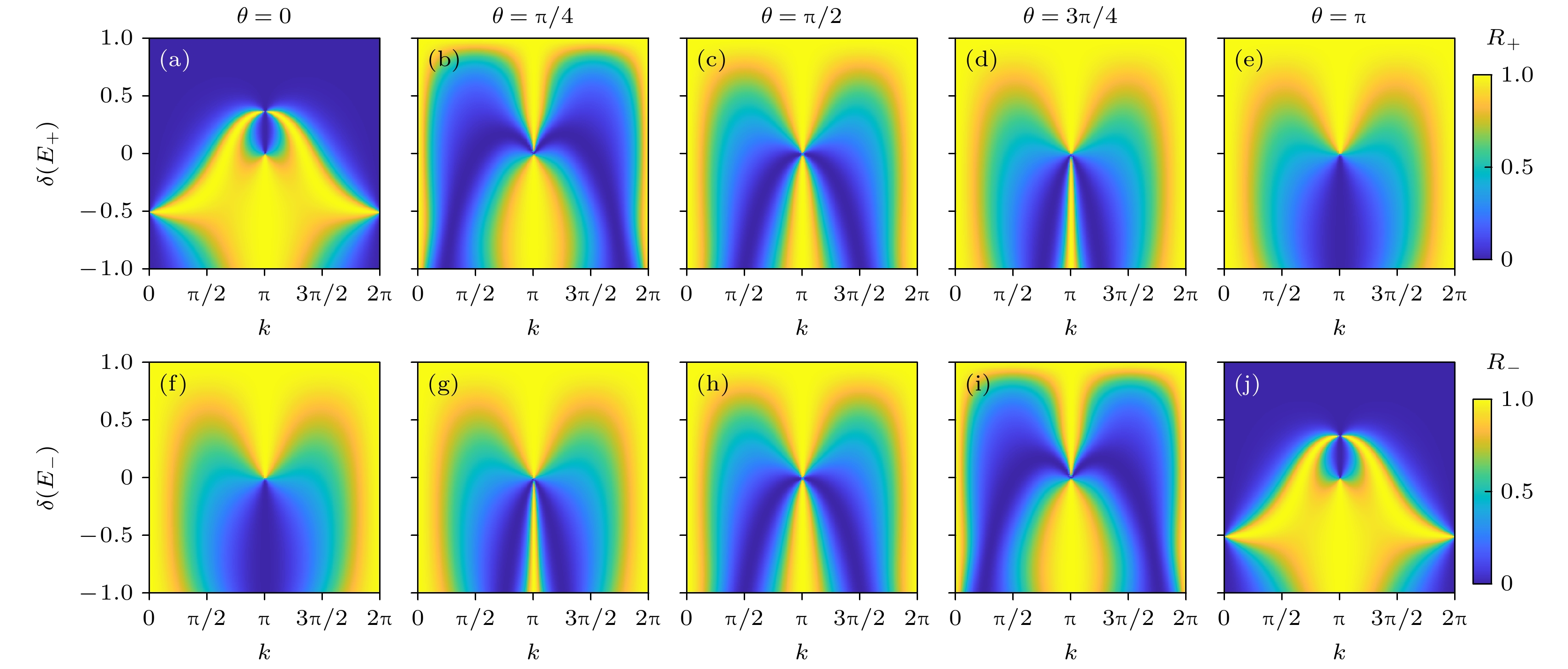
图 3 不同人工规范场相位$\theta $下, 反射系数$R$随$k$和$\delta $的变化(AB构型) (a)—(e)单光子能量为$ {E_ + } $时, 反射系数${R_ + }$随$\theta $的变化; (f)—(j)单光子能量为$ {E_ - } $时, 反射系数$ {R_ - } $随$\theta $的变化, 其他参数设置为$\varDelta = 0$, ${J_{\text{a}}} = {J_{\text{b}}} = J = 1$; 人工规范场相位$\theta $的具体取值 (a), (f) $\theta = 0$; (b), (g) $\theta = {\text{π}}/4$; (c), (h) $\theta = {\text{π}}/2$; (d), (i) $\theta = 3{\text{π}}/4$; (e), (j) $\theta = {\text{π}}$
Figure 3. Variation of the reflection coefficient $R$ with $k$ and $\delta $ for different artificial gauge field phases $\theta $(AB configuration): (a)–(e) ${R_ + }$ as a function of $\theta $ for a single-photon energy $ {E_ + } $; (f)–(j) $ {R_ - } $ as a function of $\theta $ for a single-photon energy $ {E_ - } $. Other parameters are set to $\varDelta = 0$, ${J_{\text{a}}} = {J_{\text{b}}} = J = 1$. Specific values of the artificial gauge field phase $\theta $ are as follows: (a), (f) $\theta = 0$; (b), (g) $\theta = {\text{π}}/4$; (c), (h) $\theta = {\text{π}}/2$; (d), (i) $\theta = 3{\text{π}}/4$; (e), (j) $\theta = {\text{π}}$.
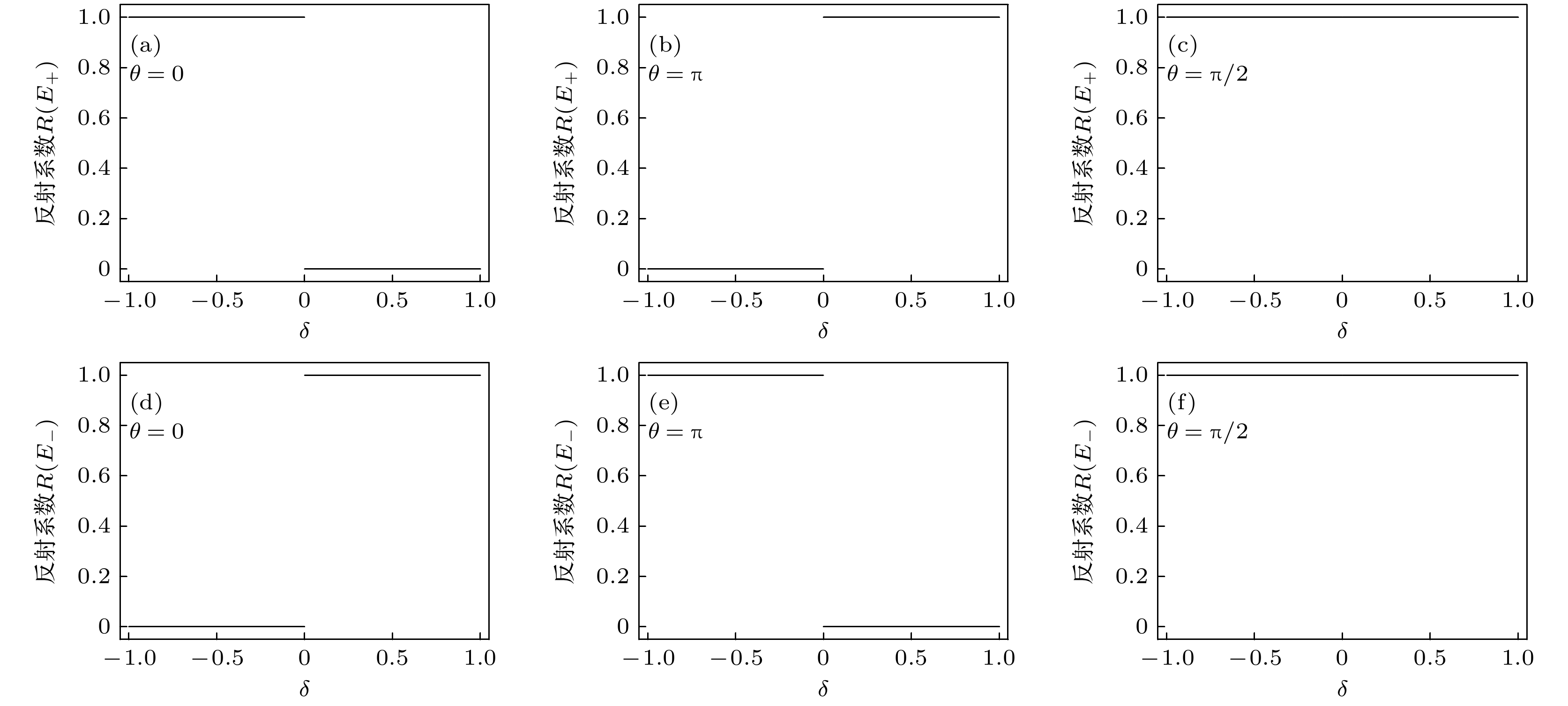
图 4 反射系数$R$随$\delta $的变化 (a)—(c)单光子能量为$ {E_ + } $时, 反射系数$R$随$\delta $的变化; (d)—(f)单光子能量为$ {E_ - } $时, 反射系数$R$随$\delta $的变化; 其他参数设置为$\varDelta = 0$, $k = \pi $, ${J{\mathrm{a}}} = {J{\mathrm{b}}} = J = 1$. 人工规范场相位$\theta $具体取值为 (a), (d) $\theta = 0$; (b), (e) $\theta = \pi $; (c), (f) $\theta = \pi /2$
Figure 4. Variation of reflection coefficient $R$ with $\delta $: (a)–(c) $R$ as a function of $\delta $ for a single photon energy $ {E_ + } $; (d)–(f) $R$ as a function of $\delta $ for a single photon energy $ {E_ - } $; Other parameters are set to $\varDelta = 0$, $k = \pi $, ${J{\mathrm{a}}} = {J_{\text{b}}} = J = 1$. Specific values of the artificial gauge field phase $\theta $ are as follows: (a), (d) $\theta = 0$; (b), (e) $\theta = \pi $; (c), (f) $\theta = \pi /2$.
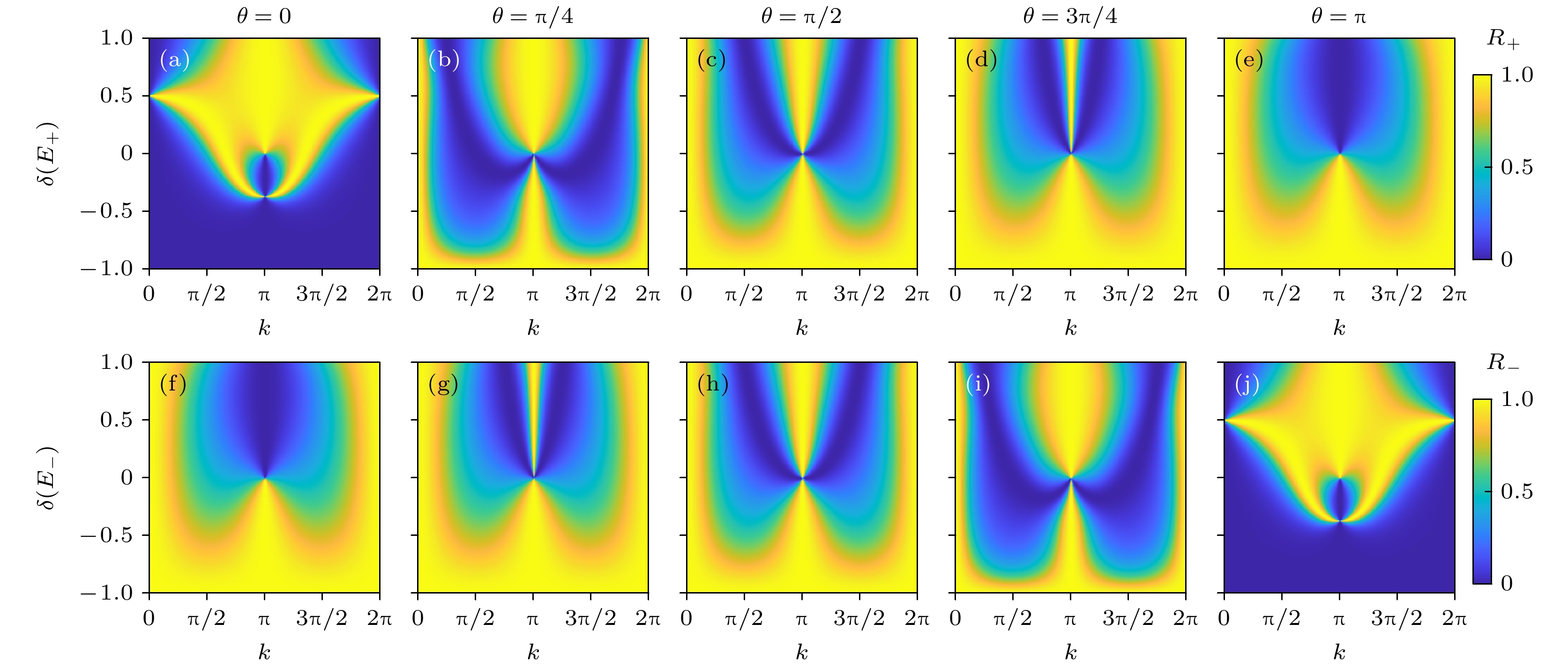
图 5 不同人工规范场相位$\theta $下, 反射系数$R$随$k$和$\delta $的变化(BA构型) (a)—(e)单光子能量为$ {E_ + } $时, 反射系数${R_ + }$随$\theta $的变化; (f)—(j)单光子能量为$ {E_ - } $时, 反射系数$ {R_ - } $随$\theta $的变化, 其他参数设置为$\varDelta = 0$, ${J_{\text{a}}} = {J_{\text{b}}} = J = 1$; 人工规范场相位$\theta $的具体取值为 (a), (f) $\theta = 0$; (b), (g) $\theta = {\text{π}}/4$; (c), (h) $\theta = {\text{π}}/2$; (d), (i) $\theta = 3{\text{π}}/4$; (e), (j) $\theta = {\text{π}}$
Figure 5. Variation of the reflection coefficient $R$ with $k$ and $\delta $ for different artificial gauge field phases $\theta $(AB configuration): (a)–(e) ${R_ + }$ as a function of $\theta $ for a single-photon energy $ {E_ + } $; (f)–(j) $ {R_ - } $ as a function of $\theta $ for a single-photon energy $ {E_ - } $. Other parameters are set to $\varDelta = 0$, ${J_{\text{a}}} = {J_{\text{b}}} = J = 1$. Specific values of the artificial gauge field phase $\theta $ are as follows: (a), (f) $\theta = 0$; (b), (g) $\theta = {\text{π}}/4$; (c), (h) $\theta = {\text{π}}/2$; (d), (i) $\theta = 3{\text{π}}/4$; (e), (j) $\theta = {\text{π}}$.
-
[1] Sheremet A S, Petrov M I, Iorsh I V, Poshakinskiy A V, Poddubny A N 2023 Rev. Mod. Phys. 95 015002
Google Scholar
[2] Mehrabad M J, Mittal S, Hafezi M 2023 Phys. Rev. A 108 040101
Google Scholar
[3] Yan Q, Hu X, Fu Y, Lu C, Fan C, Liu Q, Feng X, Sun Q, Gong Q 2021 Adv. Opt. Mater. 9 2001739
Google Scholar
[4] Lumer Y, Bandres M A, Heinrich M, Maczewsky L J, Herzig-Sheinfux H, Szameit A, Segev M 2019 Nat. Photonics 13 339
Google Scholar
[5] Zhou L, Gong Z R, Liu Y, Sun C P, Franco N 2008 Phys. Rev. Lett. 101 100501
Google Scholar
[6] Zhou L, Yang L P, Li Y, Sun C P 2013 Phys. Rev. Lett. 111 103604
Google Scholar
[7] Kannan B, Almanakly A, Sung Y, Paolo A D, Rower D A, Braumülleret J, Melville A, Niedzielski B M, Karamlou A, Serniak K, Vepsäläinen A, Schwartz M E, Yoder J L, Winik R, Wang J I J, Orlando T P, Gustavsson S, Grover J A, Oliver W D 2023 Nat. Phys. 19 394
Google Scholar
[8] Xu H S, Jin L 2022 Phys. Rev. Res. 4 L032015
Google Scholar
[9] Xu H S, Jin L 2023 Phys. Rev. Res. 5 L042005
Google Scholar
[10] Zhou L, Dong H, Liu Y, Sun C P, Nori F 2008 Phys. Rev. A 78 063827
Google Scholar
[11] Liao J Q, Huang J F, Liu Y, Kuang L M, Sun C P 2009 Phys. Rev. A 80 014301
Google Scholar
[12] Liao J Q, Gong Z R, Zhou L, Liu Y, Sun C P, Nori F 2010 Phys. Rev. A 81 042304
Google Scholar
[13] Zhou L, Kuang L M 2010 Phys. Rev. A 82 042113
Google Scholar
[14] Liao J Q, Cheung H K, Law C K 2012 Phys. Rev. A 85 025803
Google Scholar
[15] Zhou L, Chang Y, Dong H, Kuang L M, Sun C P 2012 Phys. Rev. A 85 013806
Google Scholar
[16] Liao J Q, Law C K 2013 Phys. Rev. A 87 043809
Google Scholar
[17] Wang Z H, Zhou L, Li Y, Sun C P 2014 Phys. Rev. A 89 053813
Google Scholar
[18] Xu X W, Chen A X, Li Y, Liu Y 2017 Phys. Rev. A 95 063808
Google Scholar
[19] Jin L 2018 Phys. Rev. A 98 022117
Google Scholar
[20] Wang Z, Du L, Li Y, Liu Y 2019 Phys. Rev. A 100 053809
Google Scholar
[21] Jin L, Song Z 2021 Chinese Phys. Lett. 38 024202
Google Scholar
[22] Nie W, Shi T, Nori F, Liu Y 2021 Phys. Rev. Appl. 15 044041
Google Scholar
[23] Yin X L, Liu Y H, Huang J F, Liao J Q 2022 Phys. Rev. A 106 013715
Google Scholar
[24] Tang J S, Nie W, Tang L, Chen M, Su X, Lu Y, Nori F, Xia K 2022 Phys. Rev. Lett. 128 203602
Google Scholar
[25] Zhou J, Yin X L, Liao J Q 2023 Phys. Rev. A 107 063703
Google Scholar
[26] Xu H S, Jin L 2023 Phys. Rev. Res. 5 L042005
Google Scholar
[27] Xu H S, Jin L 2024 Phys. Rev. Res. 6 L022006
Google Scholar
[28] Bello M, Platero G, Cirac J I, González-Tudela A 2019 Sci. Adv. 5 eaaw0297
Google Scholar
[29] Kim E, Zhang X, Ferreira V S, Banker J, K. Iverson J, Sipahigil A, Bello M, González-Tudela A, Mirhosseini M, Painter O 2021 Phys. Rev. X 11 011015
[30] Joshi C, Yang F, Mirhosseini M 2023 Phys. Rev. X 13 021039
[31] Cheng W, Wang Z, Liu Y 2022 Phys. Rev. A 106 033522
Google Scholar
DownLoad:
Metrics
- Abstract views: 317
- PDF Downloads: 14
- Cited By: 0
