-
The study of atomic and molecular structure imaging is of great significance in revealing the microscopic nature of matter and promoting the frontier development of materials science and life science. The rapid development of femtosecond laser technology provides a new method for detecting atomic and molecular structures on an ultrafast time scale, such as strong-field tomography scheme. Strong-field tomography uses strong-field driven electron rescattering to detect the structure of oriented molecules. The advantage of this scheme is that it does not require priori knowledge of atomic differential cross-sections. Using the strong-field tomography scheme, the structural extraction of homonuclear diatomic molecules can be realized successfully. However, it is currently unclear whether this imaging scheme is applicable to the heteronuclear molecular system with more complex cross section of the electron. In this work, heteronuclear diatomic molecules are taken for example and the strong-field tomography scheme is used to study the imaging of the molecular structure. By solving the time-dependent Schrödinger equation, the variation of the photoelectron yield with the orientation angle of the molecular axis is obtained. Next, a fitting method for the variation of the photoelectron yields of the heteronuclear molecules with the orientation angle is presented, and then the fitted value of the internuclear separation is obtained. It is found that the fitting result is comparable to the real molecular internuclear separation, indicating that the strong-field tomography scheme is also suitable for the extraction of heteronuclear molecular structural information.
-
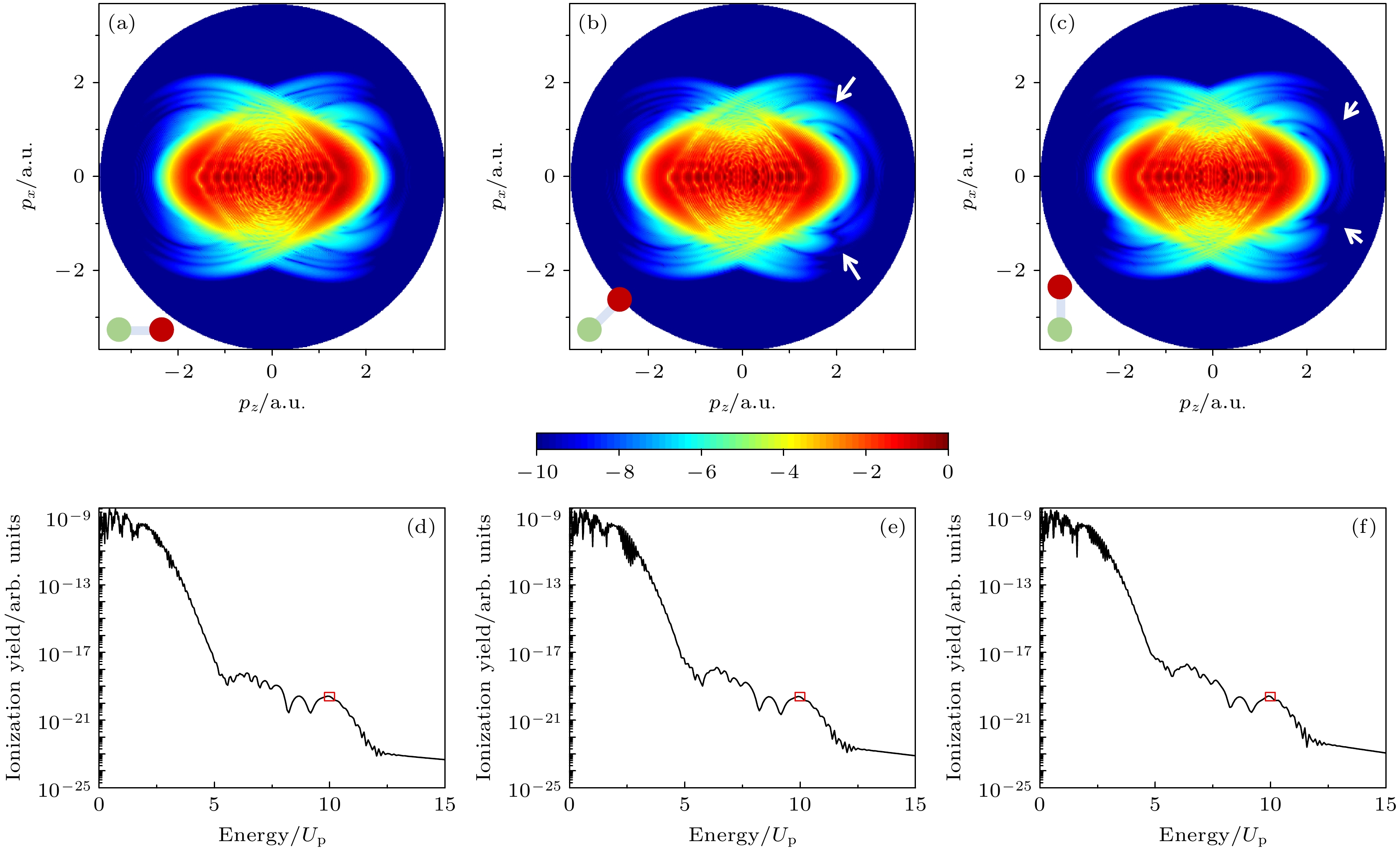
图 1 (a)—(c)通过TDSE计算得到的不同取向角下异核双原子分子的二维光电子动量分布, 其中分子取向角θL分别为(a) 0°, (b) 60°和(c) 90°, 左下角展示分子取向的示意图; (b)和(c)中两个白色箭头指向以z轴为对称轴的二维动量谱上下出现明显不对称的区域; (d)—(f)为提取出来的沿激光极化方向(z轴)的光电子能谱, 其中红色框区域代表高阶阈上电离谱平台结构的截止位置, 10Up.
Figure 1. (a)–(c) Two-dimensional photoelectron momentum distributions of heteronuclear diatomic molecules at different orientation angles calculated with TDSE. The molecular orientation angles are (a) 0°, (b) 60°, and (c) 90°. The lower left corner shows a schematic diagram of the molecular orientation. The white arrows in panel (b) and (c) point to the regions of apparent asymmetry of the spectra along the z axis. (d)–(f) The extracted photoelectron spectra along the laser polarization direction (z axis). The red box areas denote the cutoff region of the high-order above-threshold ionization platform structure, 10Up.
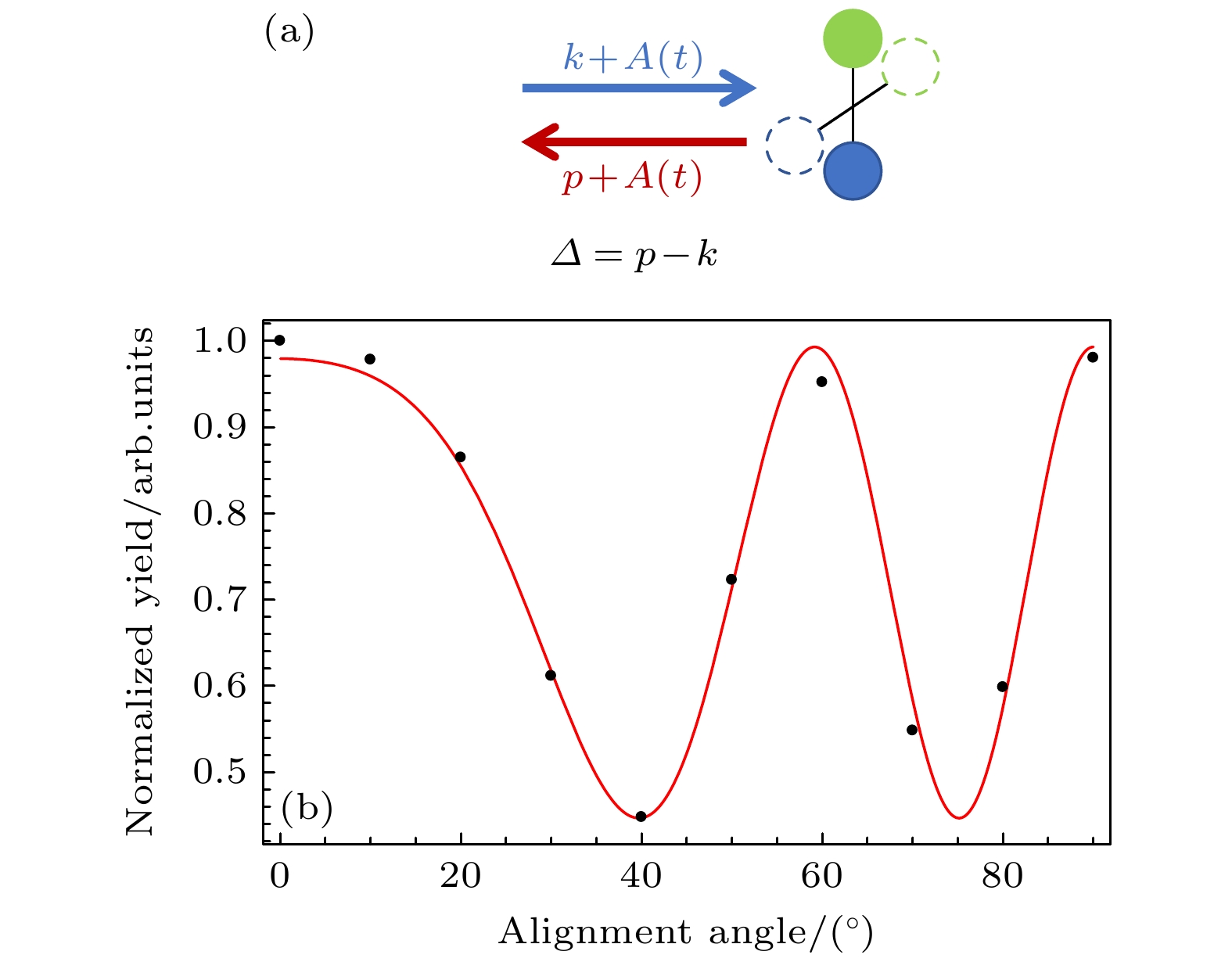
图 2 (a)不同分子轴取向角下电子再散射过程的示意图, Δ代表散射前后电子的动量变化量; (b)截止位置附近(9.83 Up—10.17 Up)的光电子产率随分子取向角的变化(黑色散点), 其中红色曲线是利用(7)式拟合的结果
Figure 2. (a) Diagram of electron rescattering at different molecular orientation angles, Δ represents the change of the electron momentum before and after the scattering; (b) the variation of the photoelectron yields at the cutoff region (9.83 Up–10.12 Up) with the orientation angle (black dots), where the red curve is the fitting result using Eq. (7).
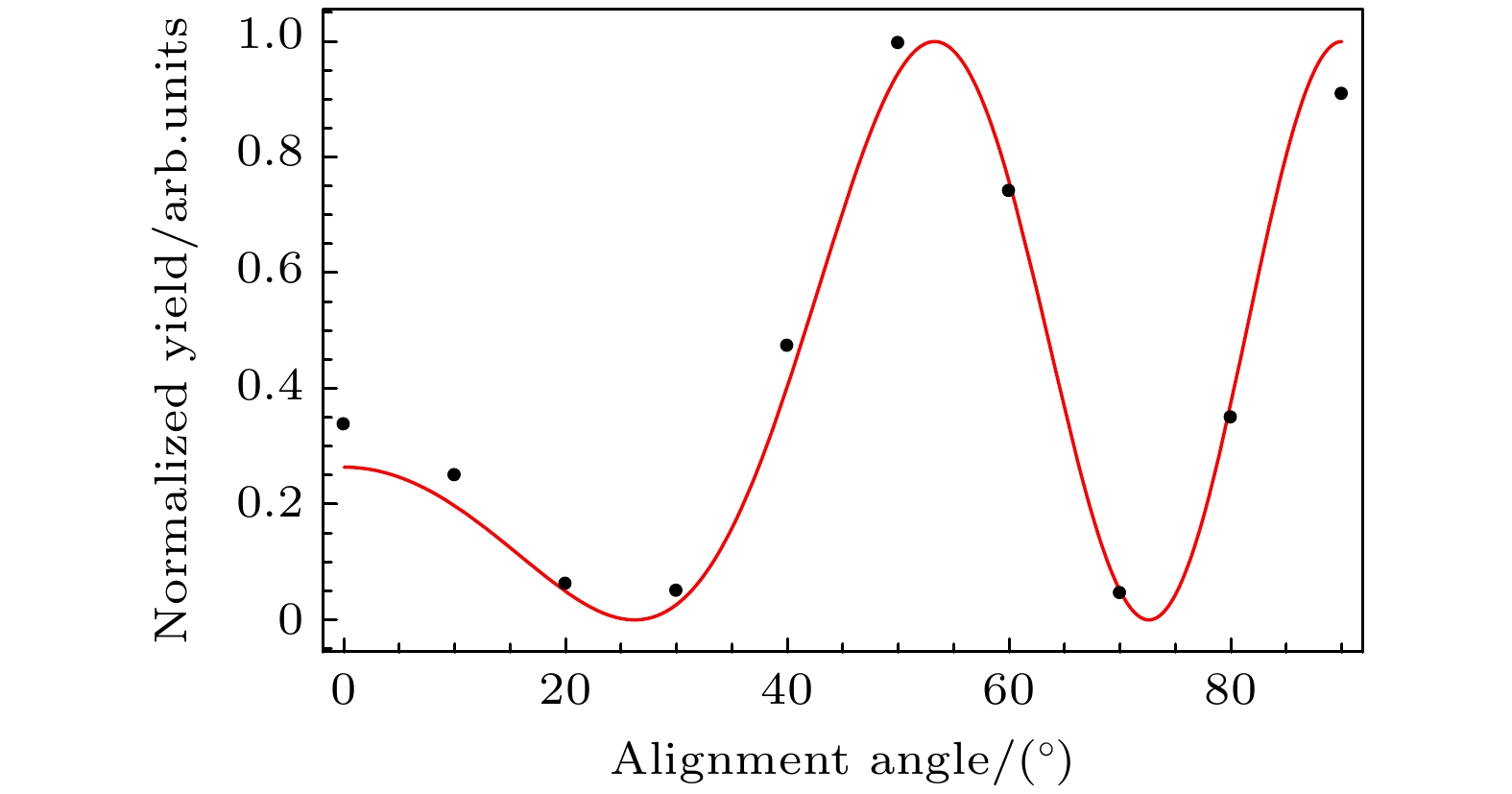
图 3 核间距Rf = 2.068 a.u.的同核双原子分子, 在高阶阈上电离谱截止位置区域的光电子产率随分子轴取向角的变化(黑色散点), 其中红色曲线是利用公式$ {\left|{\mathrm{c}}{\mathrm{o}}{\mathrm{s}}\right[(p-k){R}_{{\mathrm{f}}}{\mathrm{c}}{\mathrm{o}}{\mathrm{s}}{\theta }_{{\mathrm{L}}}\left]\right|}^{2} $进行最优拟合的结果, 使用的激光参数与图1的激光参数相同
Figure 3. For a homonuclear diatomic molecule with internuclear distance Rf = 2.068 a.u., the variation of the photoelectron yields at the cutoff region with the orientation angle (black dots). The red curve is the best fitting result according to the formula $ {\left|{\mathrm{c}}{\mathrm{o}}{\mathrm{s}}\right[(p-k){R}_{{\mathrm{f}}}{\mathrm{c}}{\mathrm{o}}{\mathrm{s}}{\theta }_{{\mathrm{L}}}\left]\right|}^{2} $. The laser parameters are the same as those used in Fig. 1.
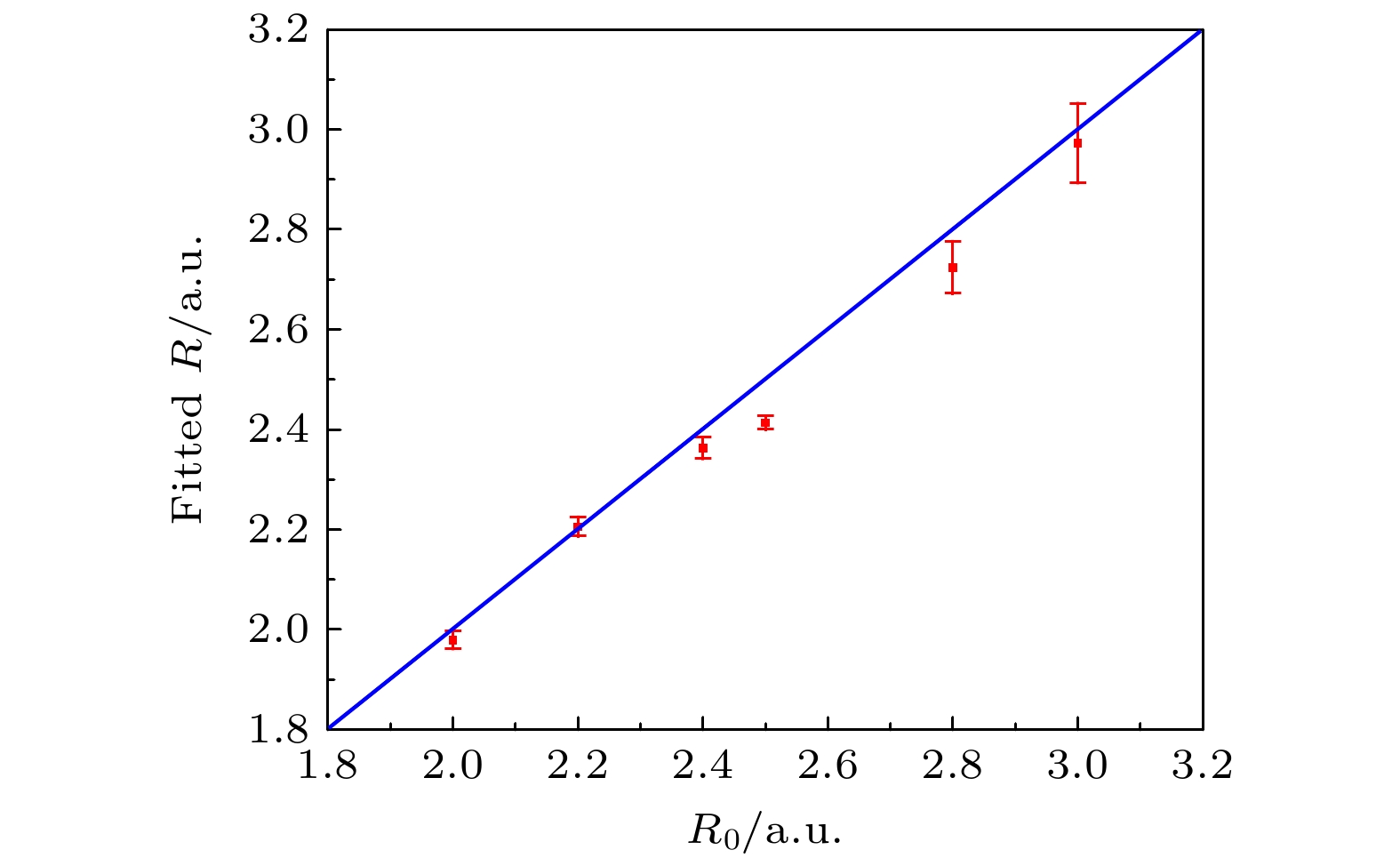
图 4 采用强场层析成像方案, 针对不同核间距R0的异核双原子分子, 拟合出的核间距, 其中红色的点代表拟合值, 其对应的误差来源于曲线拟合过程中的误差
Figure 4. Internuclear distance of heteronuclear diatomic molecules with different internuclear separation R0 obtained with strong-field tomography method. The red dots represent the fitted values, and the errors are obtained from the fitting errors of the corresponding curves.
-
[1] Corkum P B 1993 Phys. Rev. Lett. 71 1994
Google Scholar
[2] Schafer K J, Yang B, DiMauro L F, Kulander K C 1993 Phys. Rev. Lett. 70 1599
Google Scholar
[3] Becker W, Grasbon F, Kopold R, Milošević D B, Paulus G G, Walther H 2002 Adv. At. Mol. Opt. Phys. 48 35
[4] Paulus G G, Nicklich W, Xu H, Lambropoulos P, Walther H 1994 Phys. Rev. Lett. 72 2851
Google Scholar
[5] Zuo T, Bandrauk A, Corkum P B 1996 Chem. Phys. Lett. 259 313
Google Scholar
[6] Blaga C I, Xu J L, DiChiara A D, Sistrunk E, Zhang K K, Agostini P, Miller T A, DiMauro L F, Lin C D 2012 Nature 483 194
Google Scholar
[7] Meckel M, Comtois D, Zeidler D, Staudte A, Pavičić D, Bandulet H C, P´epin H, Kieffer J C, Dörner R, Villeneuve D M, Corkum P B 2008 Science 320 1478
Google Scholar
[8] Xu J, Blaga C I, Zhang K, Lai Y H, Lin C D, Miller T A, Agostini P, DiMauro L F 2014 Nat. Commun. 5 4635
Google Scholar
[9] Pullen M G, Wolter B, Le A-T, Baudisch M, Sclafani M, Pires H, Schröter C D, Ullrich J, Moshammer R, Pfeifer T, Lin C D, Biegert J 2016 Nat. Commun. 7 11922
Google Scholar
[10] Sanchez A, Amini K, Wang S-J, Steinle T, Belsa B, Danek J, Le A T, Liu X, Moshammer R, Pfeifer T, Richter M, Ullrich J, Gräfe S, Lin C D, Biegertet J 2021 Nat. Commun. 12 1520
Google Scholar
[11] Rajak D, Beauvarlet S, Kneller O, Comby A, Cireasa R, Descamps D, Fabre B, Gorfinkiel J D, Higuet J, Petit S, Rozen S, Ruf H, Thiré N, Blanchet V, Dudovich N, Pons B, Mairesse Y 2024 Phys. Rev. X 14 011015
[12] Yang Y Z, Hu X Q, Wu L, Wang Z P, Li X K, Zhou S P, Wang Z Z, Guo F M, He L H, Luo S Z, Zhang D D, Wang J G, Chen X J, Wu Y, Wang C C, Ding D J 2024 Phys. Rev. Lett. 133 113203
Google Scholar
[13] Sun R P, Lai X Y, Yu S G, Wang Y L, Xu S P, Quan W, Liu X J 2019 Phys. Rev. Lett. 122 193202
Google Scholar
[14] Busuladžić M, Gazibegović-Busuladžić A, Milošević D B, Becker W 2008 Phys. Rev. Lett. 100 203003
Google Scholar
[15] Busuladžić M, Gazibegović-Busuladžić A, Milošević D B, Becker W 2008 Phys. Rev. A 78 033412
Google Scholar
[16] Feit M D, Fleck J A, Steiger A 1982 J. Comput. Phys. 47 412
Google Scholar
[17] Chelkowski S, Foisy C, Bandrauk A D 1998 Phys. Rev. A 57 1176
Google Scholar
[18] Tong X M, Watahiki S, Hino K, Toshima N 2007 Phys. Rev. Lett. 99 093001
Google Scholar
[19] Huismans Y, Rouzée A, Gijsbertsen A, Jungmann J H, Smolkowska A S, Logman P S W M, Lépine F, Cauchy C, Zamith S, Marchenko T, Bakker J M, Berden G, Redlich B, Meer A F G, Muller H G, Vermin W, Schafer K J, Spanner M, Ivanov, M Y, Smirnova O, Bauer D, Popruzhenko S V, Vrakking M J J 2011 Science 331 61
Google Scholar
[20] Porat G, Alon G, Rozen S, Pedatzur O, Krüger M, Azoury D, Natan A, Orenstein G, Bruner B D, Vrakking M J J, Dudovich N 2018 Nat. Commun. 9 2805
Google Scholar
DownLoad:
Metrics
- Abstract views: 38
- PDF Downloads: 2
- Cited By: 0
