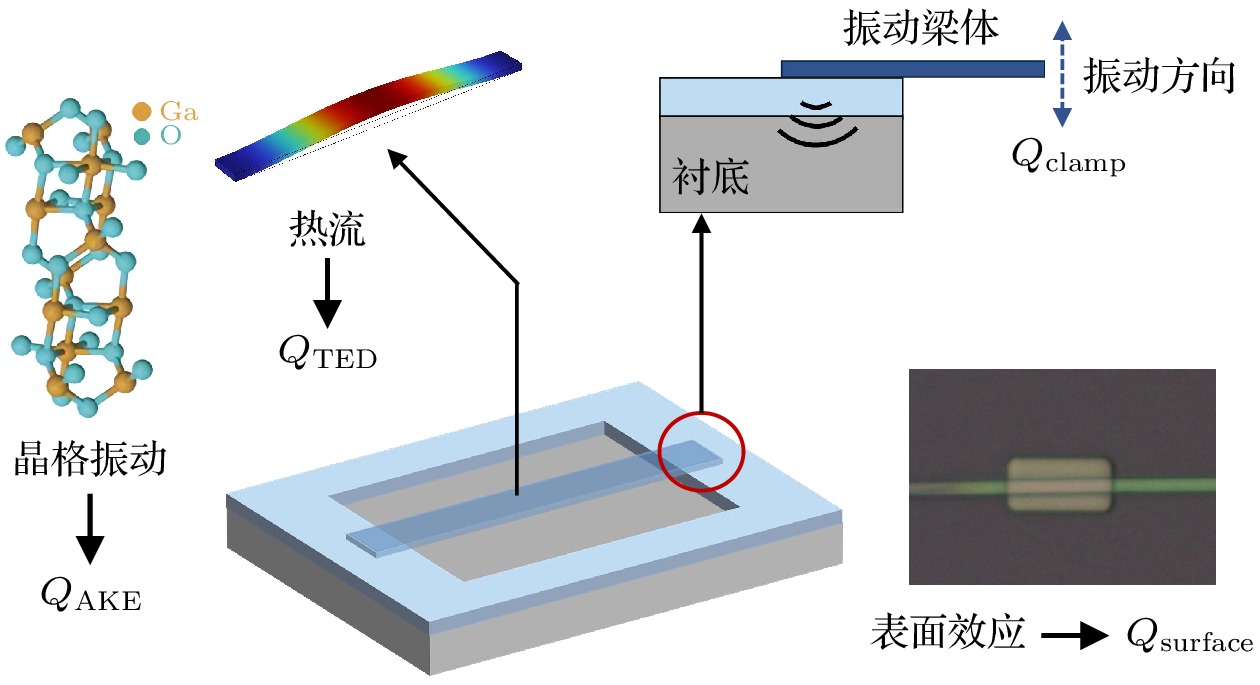
-
Beta-gallium oxide (β-Ga2O3), an emerging ultrawide bandgap (~4.8 eV) semiconductor, exhibits excellent electrical properties and cost advantages, being made as a promising candidate for high-power, high-frequency, and optoelectronic applications. Furthermore, its superior mechanical properties, including a Young’s modulus of 261 GPa, a mass density of 5950 kg/m³, and an acoustic velocity of 6623 m/s, make it particularly attractive for realizing high-frequency micro- and nanoelectromechanical system (M/NEMS) resonators. In this work, the energy dissipation mechanisms are investigated in two different β-Ga2O3 NEMS resonator geometries – doubly-clamped beams (10.5–20.8 μm length) and circular drumheads (3.3–5.3 μm diameter) – through theoretical analysis, finite element model (FEM) simulations, and experimental measurements under vacuum condition (<50 mTorr). The dominant energy dissipation mechanisms in resonators are investigated, including Akhiezer damping (AKE), thermoelastic damping (TED), clamping loss, and surface loss, by using a combined theoretical and FEM approach. Experimentally, the resonators are made by employing mechanical exfoliation combined with dry transfer techniques, yielding device thickness of 30–500 nm as verified by atomic force microscopy (AFM). Subsequently, laser interferometry is used to characterize the resonator dynamics. The resonant frequency f is obtained in a range of 5–75 MHz and the quality factor Q is approximately 200–1700 obtained through Lorentzian fitting of the resonant spectra, thus verifying the theoretical and simulation results. Our analysis indicates that surface loss and clamping loss are the main limiting factors for the Q values of current β-Ga2O3 resonators. Conversely, AKE and TED are mainly affected by material properties and resonator geometry, thus setting an upper limit for the achievable Q values with f×Q product reaching up to 1014 Hz. Our study provides a comprehensive framework integrating both theoretical analysis and experimental validation for understanding the complex energy dissipation mechanism inside a β-Ga2O3 NEMS resonator, and optimizes Q value through strain engineering and phonon crystal anchoring. These findings provide essential guidance for optimizing the performance and modulating the bandwidth of β-Ga2O3 NEMS resonator in high-frequency and high-power applications. 
[1] Ning S T, Huang S, Zhang Z Y, Zhao B, Zhang R Q, Qi N, Chen Z Q 2022 Phys. Chem. Chem. Phys. 24 12052
Google Scholar
[2] Zhou M, Zhou H, Huang S, Si M W, Zhang Y H, Luan T T, Yue H Q, Dang K, Wang C L, Liu Z H, Zhang J C, Hao Y 2023 2023 International Electron Devices Meeting Francisco, CA, USA, December 9–13, 2023 p1
[3] Chen H, Li Z, Zhang Z Y L, Liu D H, Zeng L R, Yan Y R, Chen D Z, Feng Q, Zhang J C, Hao Y, Zhang C F 2024 Semicond. Sci. Technol. 39 063001
Google Scholar
[4] Zheng X Q, Zhao H P, Feng P X L 2022 Appl. Phys. Lett. 120 040502
Google Scholar
[5] Labed M, Sengouga N, Prasad C V, Henini M, Rim Y S 2023 Mater. Today Phys. 36 101155
Google Scholar
[6] Liang Y, Yu H, Wang H, Zhang H C, Cui T J 2022 Chip 1 100030
Google Scholar
[7] Li H, Zhou Z H, Zhao Y Z, Li Y 2023 Chip 2 100049
Google Scholar
[8] Soref R, Leonardis F D 2022 Chip 1 100011
Google Scholar
[9] Lu C C, Yuan H Y, Zhang H Y, Zhao W, Zhang N E, Zheng Y J, Elshahat S, Liu Y C 2022 Chip 1 100025
Google Scholar
[10] Wang L M, Zhang P C, Liu Z H, Wang Z H, Yang R 2023 Chip 2 100038
Google Scholar
[11] Abdolvand R, Bahreyni B, Lee J E Y, Nabki F 2016 Micromachines 7 160
Google Scholar
[12] Feng T R, Yuan Q, Yu D L, Wu B, Wang H 2022 Micromachines 13 2195
Google Scholar
[13] Aoust G, Levy R, Bourgeteau B, Traon O L 2015 Sens. Actuators A: Phys. 230 126
Google Scholar
[14] Sun Y X, Tohmyoh H 2009 J. Sound Vib. 319 392
Google Scholar
[15] Schmid S, Hierold C 2008 J. Appl. Phys. 104 093516
Google Scholar
[16] Imboden M, Mohanty P 2014 Phys. Rep. 534 89
Google Scholar
[17] Rodriguez J, Chandorkar S A, Watson C A, Glaze G M, Ahn C H, Ng E J, Yang Y S, Kenny T W 2019 Sci. Rep. 9 2244
Google Scholar
[18] Pearton S J, Yang J C, Cary P H, Ren F, Kim J, Tadjer M J, Mastro M A 2018 Appl. Phys. Rev. 5 011301
Google Scholar
[19] Bokaian A 1990 J. Sound Vib. 142 481
Google Scholar
[20] Suzuki H, Yamaguchi N, Izumi H 2009 Acoust. Sci. Technol. 30 348
Google Scholar
[21] Cimalla V, Foerster C, Will F, Tonisch K, Brueckner K, Stephan R, Hein M E, Ambacher O, Aperathitis E 2006 Appl. Phys. Lett. 88 253501
Google Scholar
[22] Lee J, Wang Z H, He K L, Shan J, Feng P X L 2014 Appl. Phys. Lett. 105 023104
Google Scholar
[23] Kunal K, Aluru N R 2011 Phys. Rev. B 84 245450
Google Scholar
[24] Ghaffari S, Chandorkar S A, Wang S S, Ng E J, Ahn C H, Hong V, Yang Y S, Kenny T W 2013 Sci. Rep. 3 3244
Google Scholar
[25] Tabrizian R, Rais-Zadeh M, Ayazi F 2009 Solid-state Sensors, Actuators & Microsystems Conference Denver, CO, USA, June 21–25, 2009 p2131
[26] Chen Z J, Jia Q Q, Liu W L, Zhu Y F, Yuan Q, Yang J L, Yang F H 2021 IEEE MEMS 2021 Virtual Conference Gainesville, FL, USA, January 25–29, 2021 p964
[27] Yan S H, Liu Z, Tan C K, Zhang X Y, Li S, Shi L, Guo Y F, Tang W H 2023 Appl. Phys. Lett. 123 142202
Google Scholar
[28] Guo Z, Verma A, Wu X F, Sun F Y, Hickman A, Masui T, Kuramata A, Higashiwaki M, Jena D, Luo T F 2015 Appl. Phys. Lett. 106 111909
Google Scholar
[29] Safieddine F, Hassan F E H, Kazan M 2022 J. Solid State Chem. 312 123272
Google Scholar
[30] Prabhakar S, Vengallatore S 2007 J. Micromech. Microeng. 17 532
Google Scholar
[31] Lifshitz R, Roukes M L 2000 Phys. Rev. B 61 5600
[32] Sun Y X, Saka M 2010 J. Sound Vib. 329 328
Google Scholar
[33] Cheng Z Z, Hanke M, Galazka Z, Trampert A 2018 Appl. Phys. Lett. 113 182102
Google Scholar
[34] Ko J H, Jeong J, Choi J, Cho M 2011 Appl. Phys. Lett. 98 171909
Google Scholar
[35] Yang J L, Ono T, Esashi M 2002 J. Microelectromech. Syst. 11 775
Google Scholar
[36] Mohanty P, Harrington D A, Ekinci K L, Yang Y T, Murphy M J, Roukes M L 2002 Phys. Rev. B 66 085416
Google Scholar
[37] Villanueva L G, Schmid S 2014 Phys. Rev. Lett. 113 227201
Google Scholar
[38] Zheng X Q, Tharpe T, Enamul Hoque Yousuf S M, Rudawski N G, Feng P X L 2022 ACS Appl. Mater. Interfaces 14 36807
Google Scholar
[39] Bercioux D, Buchs G, Grabert H, Groning O 2011 Phys. Rev. B 83 165439
Google Scholar
[40] Wang C H, Ning Y H, Zhao W Y, Yi G X, Huo Y 2023 Sens. Actuator A: Phys. 359 114456
Google Scholar
[41] Ahamed M J, Senkal D, Shkel A M 2014 2014 International Symposium on Inertial Sensors and Systems (INERTIAL) Laguna Beach, CA, USA, February 25–26, 2014 p59
[42] Zheng X Q, Lee J, Rafique S, Han L, Zorman C A, Zhao H P, Feng P X L 2017 ACS Appl. Mater. Interfaces 9 43090
Google Scholar
[43] Li S S, Lin Y W, Xie Y, Ren Z Y, Nguyen C T C 2004 17th Int. IEEE Micro Electro Mechanical Systems Conf Maastricht, The Netherlands, January 25–29, 2004 p821
[44] 郑贤德, 甄嘉鹏, 邱静, 刘冠军 2023 仪器仪表学报 44 206
Google Scholar
Zheng X D, Zhen J P, Qiu J, Liu G J 2023 Chin. J. Sci. Instrum. 44 206
Google Scholar
-
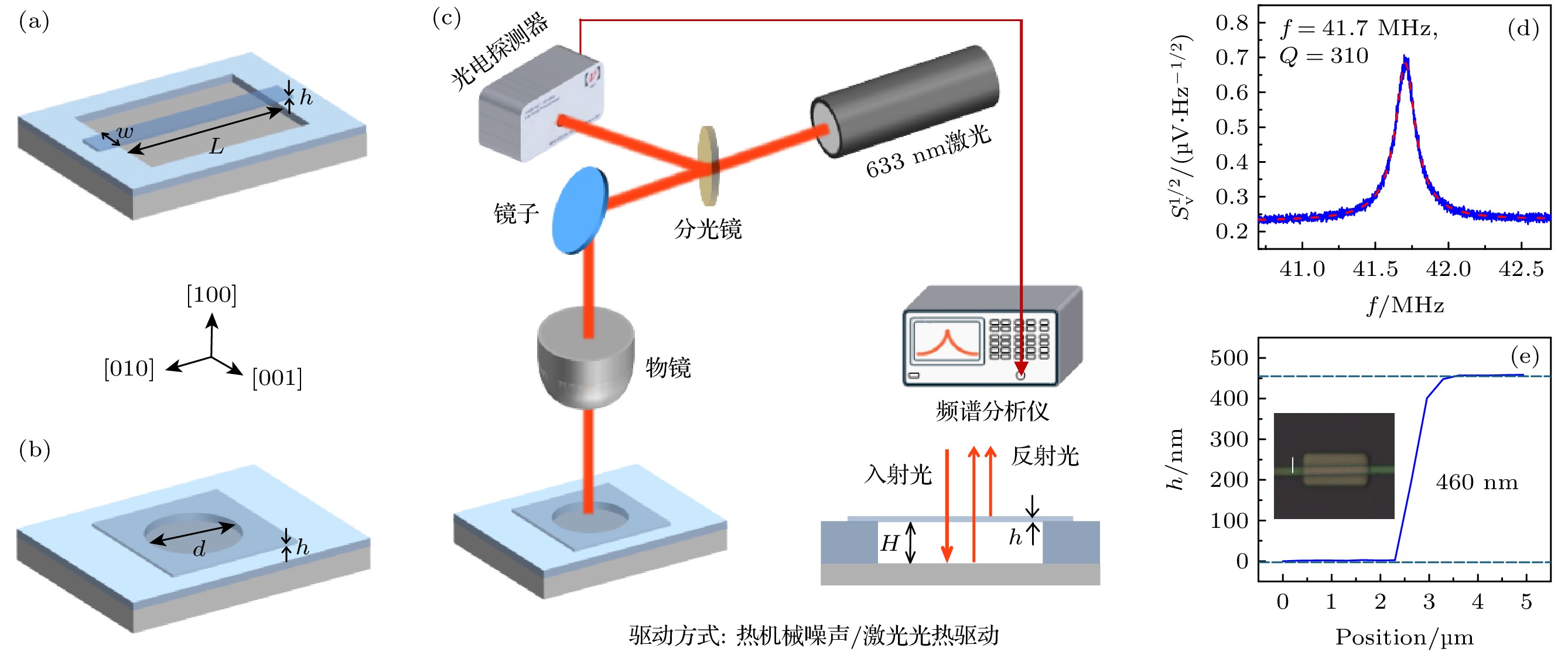
图 1 (a) 双端固支谐振器结构示意图; (b) 圆形鼓面谐振器结构示意图; (c) 激光干涉测量系统原理图, 其中h, H分别表示材料厚度与沟槽深度; (d) 谐振器典型频谱曲线及其洛伦兹拟合, 该器件为d = 3.3 μm, h = 45 nm的圆形鼓面谐振器; (e) AFM扫描曲线, 插图为所测量的双端固支结构谐振器, 其中短实线为AFM探针的扫描路径
Figure 1. (a) Illustration of a doubly-clamped resonator; (b) illustration of a circular drumhead resonator; (c) schematic of the laser interferometry measurement system, where h and H denote the material thickness and trench depth, respectively; (d) typical spectrum of a circular drumhead resonator with d = 3.3 μm, h = 45 nm and its Lorentzian fitting; (e) AFM scanning curve with inset showing the scanning path, where the short solid line is the scanning path of the AFM probe.
图 2 不同能量耗散机制
Figure 2. Different mechanisms of energy dissipation.
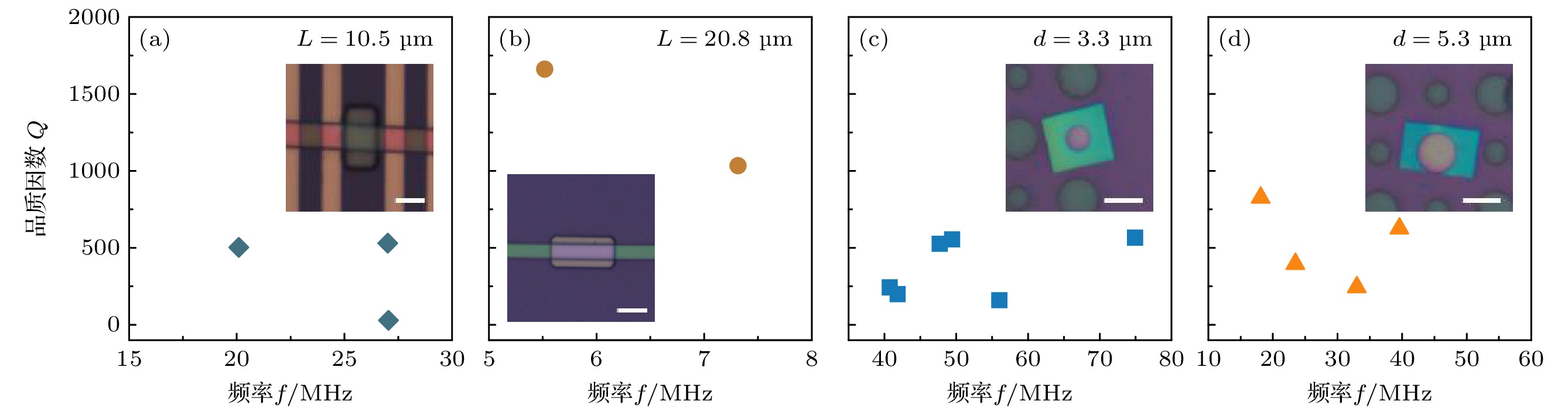
图 3 不同谐振器的f和Q测量值, 插图显示了对应典型器件的显微图, L与d分别表示双端固支悬空结构的长度与圆形鼓面悬空结构的直径 (a), (b) L = 10.5 μm和20.8 μm的双端固支器件, 比例尺为10 μm; (c), (d) d = 3.3 μm和5.3 μm的圆形鼓面器件, 比例尺为5 μm
Figure 3. Measured values of f and Q for various resonators, with the insets showing the corresponding micrographs of typical devices: (a), (b) Doubly-clamped resonators with L = 10.5 μm and 20.8 μm, each with a scale bar of 10 μm; (c), (d) circular drumhead resonators with d = 3.3 μm and 5.3 μm, each with a scale bar of 5 μm.
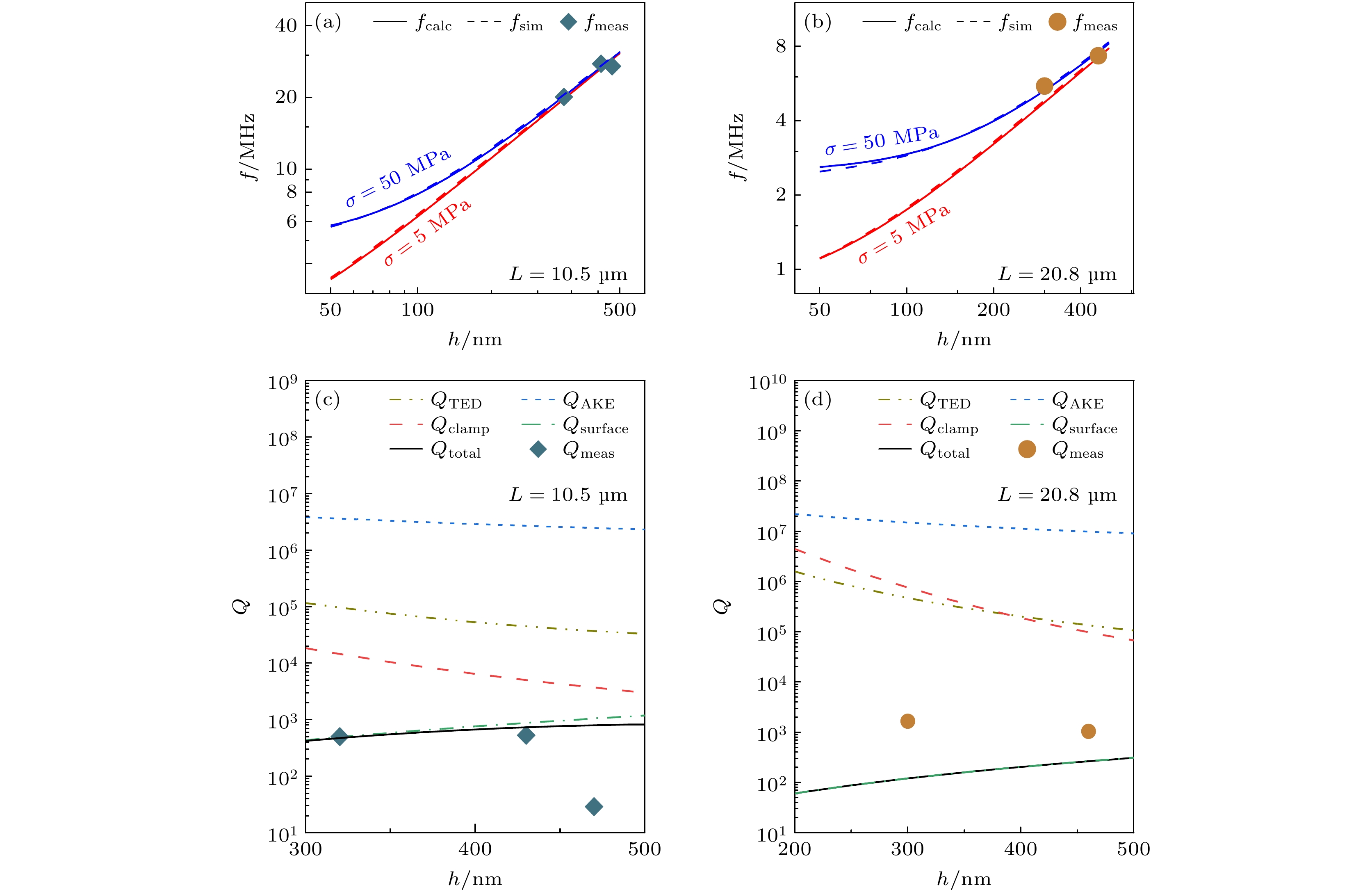
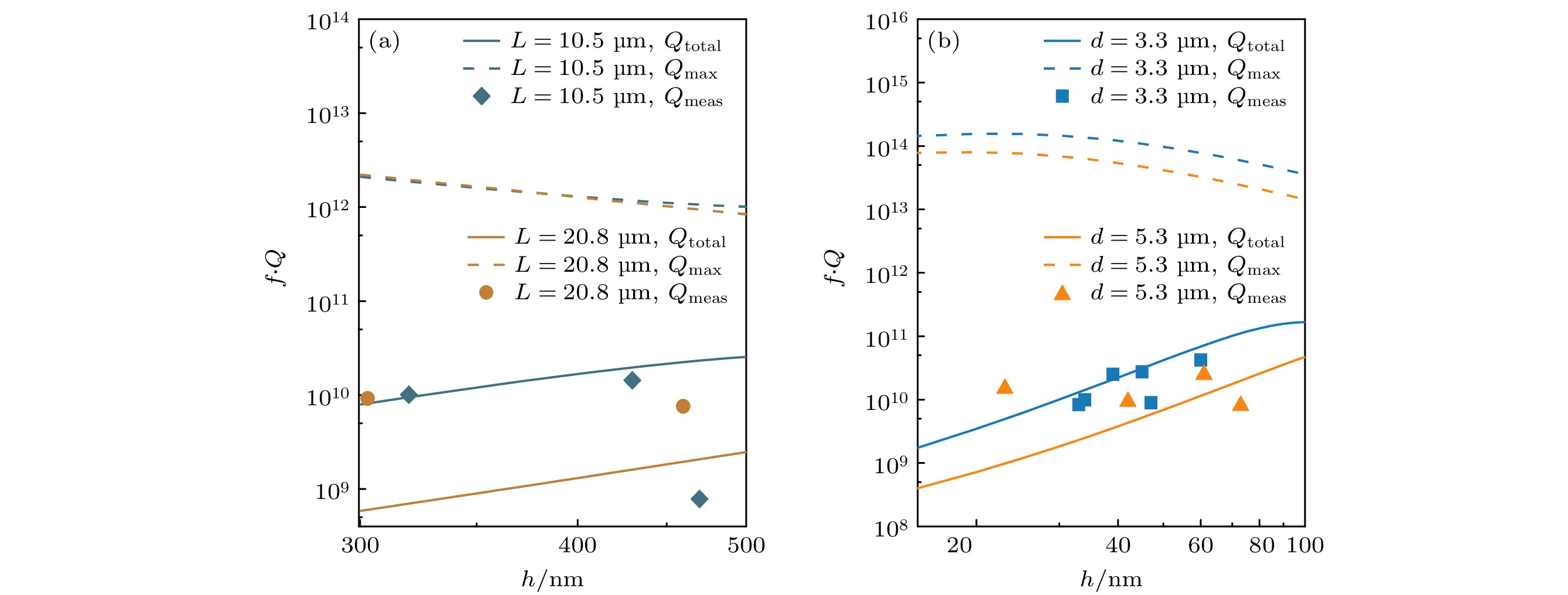
图 4 (a) L = 10.5 μm和(b) L = 20.8 μm两种双端固支器件在不同内应力 (红色曲线为σ = 5 MPa, 蓝色曲线为σ = 50 MPa) 下谐振频率f的计算值fcalc(实线)、仿真值fsim(虚线)与测量值fmeas(散点); (c) L = 10.5 μm和(d) L = 20.8 μm两种双端固支谐振器在不同耗散机制限制下的Q值、通过(1)式计算得到的Qtotal以及测量值Qmeas
Figure 4. Calculated value fcalc (solid line), simulated value fsim (dashed line), and measured value fmeas (scattered symbols) of the resonant frequency f under different internal stresses (σ = 5 MPa for red curve and σ = 50 MPa for blue curve) for doubly-clamped resonators: (a) L = 10.5 μm and (b) L = 20.8 μm, Q values limited by different loss mechanisms, Qtotal calculated by Eq. (1), and measured Qmeas for doubly-clamped resonators of (c) L = 10.5 μm and (d) L = 20.8 μm.
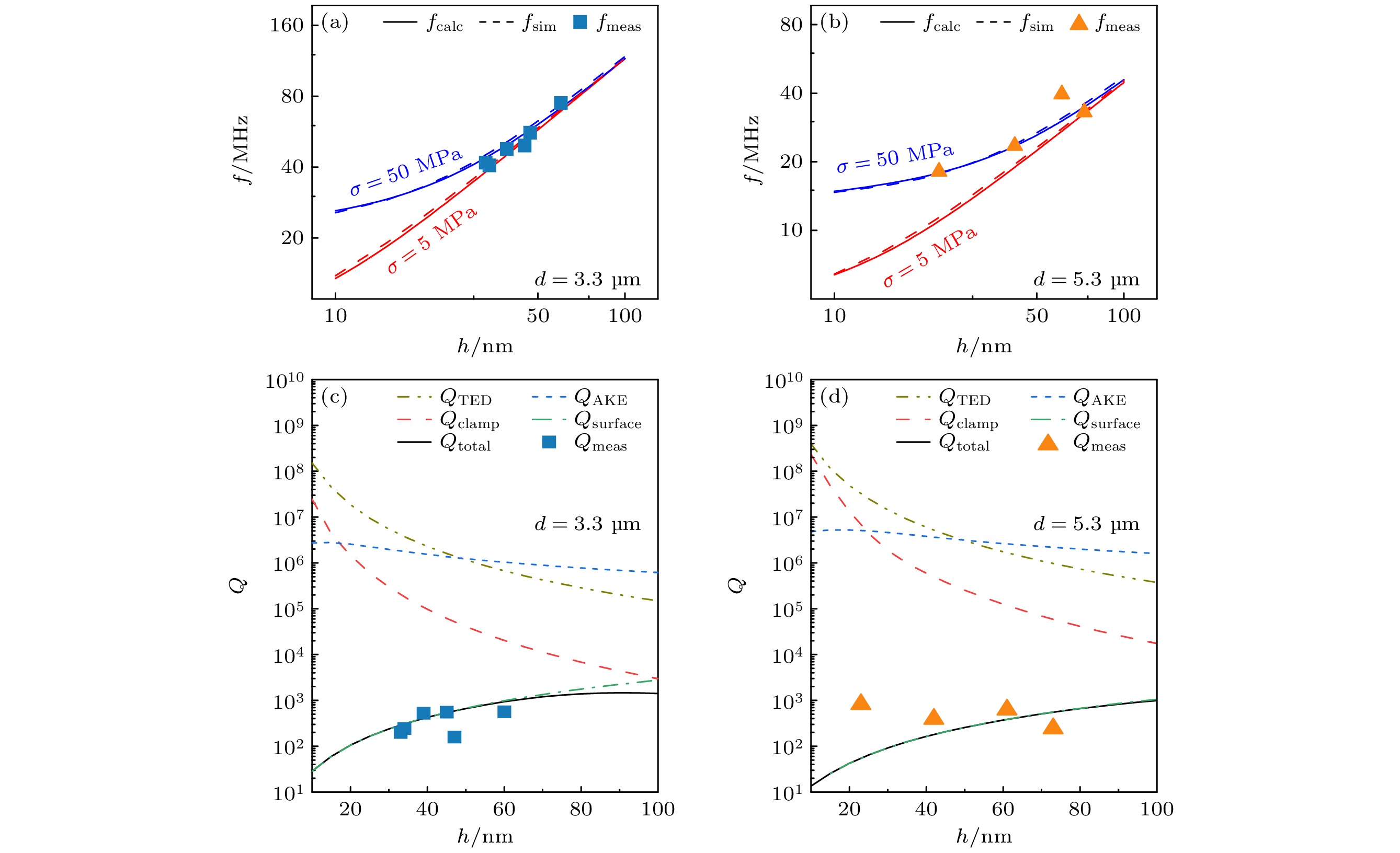
图 5 (a) d = 3.3 μm和(b) d = 5.3 μm两种圆形鼓面器件在不同内应力(红色曲线为σ = 5 MPa, 蓝色曲线为σ = 50 MPa)下谐振频率f的计算值fcalc(实线)、仿真值fsim(虚线)与测量值fmeas(散点), 其中实线为计算值, 虚线为仿真值; (c) d = 3.3 μm和(d) d = 5.3 μm两种圆形鼓面器件在不同耗散机制限制下的Q值、通过(1)式计算得到的Qtotal以及测量值Qmeas
Figure 5. Calculated value fcalc (soild line), simulated value fsim (dashed line), and measured value fmeas (scattered line) of the resonant frequency f under different internal stresses (σ = 5 MPa for red curve and σ = 50 MPa for blue curve) of drumhead resonators: (a) d = 3.3 μm and (b) d = 5.3 μm. Q values limited by different loss mechanisms, Qtotal calculated by Eq. (1), and measured Qmeas for drumhead resonators of (c) d = 3.3 μm and (d) d = 5.3 μm.
图 6 (a) 双端固支与(b)圆形鼓面谐振器的不同f × Q值, 包括Qtotal (实线), Qmax (虚线), Qmeas (散点)
Figure 6. Different f × Q values for doubly-clamped resonators and circular drumhead resonators, including Qtotal (solid line), Qmax (dashed line), Qmeas (scattered symbols).
表 1 β-Ga2O3的材料性能参数
Table 1. Material properties of β-Ga2O3.
物理量 值 杨氏模量EY[4]/GPa 261 密度ρ[4] /(kg·m–3) 5950 泊松比ν[4] 0.2 声速c[4]/(m·s–1) 6623 声子散射时间τs/s 双端固支: 6.37×10–13
圆形鼓面: 4.89×10–13平均Grüneisen参数γavg[27] 1.018 质量热容Cp[29] /(J·kg–1·K–1) 491 热膨胀系数α[33]/K–1 [100]: 0.10×10–6
[010]: 1.68×10–6
[001]: 1.74×10–6热导率k[28]/(W·m–1·K–1) [100]: 10.9
[010]: 27.0
[001]: 14.5
DownLoad: CSV
-
[1] Ning S T, Huang S, Zhang Z Y, Zhao B, Zhang R Q, Qi N, Chen Z Q 2022 Phys. Chem. Chem. Phys. 24 12052
Google Scholar
[2] Zhou M, Zhou H, Huang S, Si M W, Zhang Y H, Luan T T, Yue H Q, Dang K, Wang C L, Liu Z H, Zhang J C, Hao Y 2023 2023 International Electron Devices Meeting Francisco, CA, USA, December 9–13, 2023 p1
[3] Chen H, Li Z, Zhang Z Y L, Liu D H, Zeng L R, Yan Y R, Chen D Z, Feng Q, Zhang J C, Hao Y, Zhang C F 2024 Semicond. Sci. Technol. 39 063001
Google Scholar
[4] Zheng X Q, Zhao H P, Feng P X L 2022 Appl. Phys. Lett. 120 040502
Google Scholar
[5] Labed M, Sengouga N, Prasad C V, Henini M, Rim Y S 2023 Mater. Today Phys. 36 101155
Google Scholar
[6] Liang Y, Yu H, Wang H, Zhang H C, Cui T J 2022 Chip 1 100030
Google Scholar
[7] Li H, Zhou Z H, Zhao Y Z, Li Y 2023 Chip 2 100049
Google Scholar
[8] Soref R, Leonardis F D 2022 Chip 1 100011
Google Scholar
[9] Lu C C, Yuan H Y, Zhang H Y, Zhao W, Zhang N E, Zheng Y J, Elshahat S, Liu Y C 2022 Chip 1 100025
Google Scholar
[10] Wang L M, Zhang P C, Liu Z H, Wang Z H, Yang R 2023 Chip 2 100038
Google Scholar
[11] Abdolvand R, Bahreyni B, Lee J E Y, Nabki F 2016 Micromachines 7 160
Google Scholar
[12] Feng T R, Yuan Q, Yu D L, Wu B, Wang H 2022 Micromachines 13 2195
Google Scholar
[13] Aoust G, Levy R, Bourgeteau B, Traon O L 2015 Sens. Actuators A: Phys. 230 126
Google Scholar
[14] Sun Y X, Tohmyoh H 2009 J. Sound Vib. 319 392
Google Scholar
[15] Schmid S, Hierold C 2008 J. Appl. Phys. 104 093516
Google Scholar
[16] Imboden M, Mohanty P 2014 Phys. Rep. 534 89
Google Scholar
[17] Rodriguez J, Chandorkar S A, Watson C A, Glaze G M, Ahn C H, Ng E J, Yang Y S, Kenny T W 2019 Sci. Rep. 9 2244
Google Scholar
[18] Pearton S J, Yang J C, Cary P H, Ren F, Kim J, Tadjer M J, Mastro M A 2018 Appl. Phys. Rev. 5 011301
Google Scholar
[19] Bokaian A 1990 J. Sound Vib. 142 481
Google Scholar
[20] Suzuki H, Yamaguchi N, Izumi H 2009 Acoust. Sci. Technol. 30 348
Google Scholar
[21] Cimalla V, Foerster C, Will F, Tonisch K, Brueckner K, Stephan R, Hein M E, Ambacher O, Aperathitis E 2006 Appl. Phys. Lett. 88 253501
Google Scholar
[22] Lee J, Wang Z H, He K L, Shan J, Feng P X L 2014 Appl. Phys. Lett. 105 023104
Google Scholar
[23] Kunal K, Aluru N R 2011 Phys. Rev. B 84 245450
Google Scholar
[24] Ghaffari S, Chandorkar S A, Wang S S, Ng E J, Ahn C H, Hong V, Yang Y S, Kenny T W 2013 Sci. Rep. 3 3244
Google Scholar
[25] Tabrizian R, Rais-Zadeh M, Ayazi F 2009 Solid-state Sensors, Actuators & Microsystems Conference Denver, CO, USA, June 21–25, 2009 p2131
[26] Chen Z J, Jia Q Q, Liu W L, Zhu Y F, Yuan Q, Yang J L, Yang F H 2021 IEEE MEMS 2021 Virtual Conference Gainesville, FL, USA, January 25–29, 2021 p964
[27] Yan S H, Liu Z, Tan C K, Zhang X Y, Li S, Shi L, Guo Y F, Tang W H 2023 Appl. Phys. Lett. 123 142202
Google Scholar
[28] Guo Z, Verma A, Wu X F, Sun F Y, Hickman A, Masui T, Kuramata A, Higashiwaki M, Jena D, Luo T F 2015 Appl. Phys. Lett. 106 111909
Google Scholar
[29] Safieddine F, Hassan F E H, Kazan M 2022 J. Solid State Chem. 312 123272
Google Scholar
[30] Prabhakar S, Vengallatore S 2007 J. Micromech. Microeng. 17 532
Google Scholar
[31] Lifshitz R, Roukes M L 2000 Phys. Rev. B 61 5600
[32] Sun Y X, Saka M 2010 J. Sound Vib. 329 328
Google Scholar
[33] Cheng Z Z, Hanke M, Galazka Z, Trampert A 2018 Appl. Phys. Lett. 113 182102
Google Scholar
[34] Ko J H, Jeong J, Choi J, Cho M 2011 Appl. Phys. Lett. 98 171909
Google Scholar
[35] Yang J L, Ono T, Esashi M 2002 J. Microelectromech. Syst. 11 775
Google Scholar
[36] Mohanty P, Harrington D A, Ekinci K L, Yang Y T, Murphy M J, Roukes M L 2002 Phys. Rev. B 66 085416
Google Scholar
[37] Villanueva L G, Schmid S 2014 Phys. Rev. Lett. 113 227201
Google Scholar
[38] Zheng X Q, Tharpe T, Enamul Hoque Yousuf S M, Rudawski N G, Feng P X L 2022 ACS Appl. Mater. Interfaces 14 36807
Google Scholar
[39] Bercioux D, Buchs G, Grabert H, Groning O 2011 Phys. Rev. B 83 165439
Google Scholar
[40] Wang C H, Ning Y H, Zhao W Y, Yi G X, Huo Y 2023 Sens. Actuator A: Phys. 359 114456
Google Scholar
[41] Ahamed M J, Senkal D, Shkel A M 2014 2014 International Symposium on Inertial Sensors and Systems (INERTIAL) Laguna Beach, CA, USA, February 25–26, 2014 p59
[42] Zheng X Q, Lee J, Rafique S, Han L, Zorman C A, Zhao H P, Feng P X L 2017 ACS Appl. Mater. Interfaces 9 43090
Google Scholar
[43] Li S S, Lin Y W, Xie Y, Ren Z Y, Nguyen C T C 2004 17th Int. IEEE Micro Electro Mechanical Systems Conf Maastricht, The Netherlands, January 25–29, 2004 p821
[44] 郑贤德, 甄嘉鹏, 邱静, 刘冠军 2023 仪器仪表学报 44 206
Google Scholar
Zheng X D, Zhen J P, Qiu J, Liu G J 2023 Chin. J. Sci. Instrum. 44 206
Google Scholar
-
[1] Li Yu-Qing, Wang Hong-Guang, Zhai Yong-Gui, Yang Wen-Jin, Wang Yue, Li Yun, Li Yong-Dong. Influence of quality factor on operating mode of TM02 mode relativistic backwave oscillator. Acta Physica Sinica, 2024, 73(3): 035202. doi: 10.7498/aps.73.20231577 [2] Yi Zi-Qi, Wang Yan-Ming, Wang Shuo, Sui Xue, Shi Jia-Hui, Yang Yi-Han, Wang De-Yu, Feng Qiu-Ju, Sun Jing-Chang, Liang Hong-Wei. Performance of UV photodetector of mechanical exfoliation prepared PEDOT:PSS/β-Ga2O3 microsheet heterojunction. Acta Physica Sinica, 2024, 73(15): 157102. doi: 10.7498/aps.73.20240630 [3] Zhou Zhan-Hui, Li Qun, He Xiao-Min. Electron transport mechanism in AlN/β-Ga2O3 heterostructures. Acta Physica Sinica, 2023, 72(2): 028501. doi: 10.7498/aps.72.20221545 [4] Wang Lu-Xuan, Liu Yi-Tong, Shi Fang-Yuan, Qi Xian-Wen, Shen Han, Song Ying-Lin, Fang Yu. Broadband ultrafast photogenerated carrier dynamics induced by intrinsic defects in $\boldsymbol\beta$ -Ga2O3. Acta Physica Sinica, 2023, 72(21): 214202. doi: 10.7498/aps.72.20231173[5] Zhang Mao-Lin, Ma Wan-Yu, Wang Lei, Liu Zeng, Yang Li-Li, Li Shan, Tang Wei-Hua, Guo Yu-Feng. Investigation of high-temperature performance of WO3/β-Ga2O3 heterojunction deep-ultraviolet photodetectors. Acta Physica Sinica, 2023, 72(16): 160201. doi: 10.7498/aps.72.20230638 [6] Fan Si-Chen, Yang Fan, Ruan Jun. Eelectromagnetic field distribution of whispering gallery mode in a sapphire resonator. Acta Physica Sinica, 2022, 71(23): 234101. doi: 10.7498/aps.71.20221156 [7] Jiang Li-Ying, Yi Ying-Ting, Yi Zao, Yang Hua, Li Zhi-You, Su Ju, Zhou Zi-Gang, Chen Xi-Fang, Yi You-Gen. A four-band perfect absorber based on high quality factor and high figure of merit of monolayer molybdenum disulfide. Acta Physica Sinica, 2021, 70(12): 128101. doi: 10.7498/aps.70.20202163 [8] Hong Zi-Fan, Chen Hai-Feng, Jia Yi-Fan, Qi Qi, Liu Ying-Ying, Guo Li-Xin, Liu Xiang-Tai, Lu Qin, Li Li-Jun, Wang Shao-Qing, Guan Yun-He, Hu Qi-Ren. Characteristics of Ga2O3 epitaxial films on seed layer grown by magnetron sputtering. Acta Physica Sinica, 2020, 69(22): 228103. doi: 10.7498/aps.69.20200810 [9] Qi Qi, Chen Hai-Feng, Hong Zi-fan, Liu Ying-Ying, Guo Li-Xin, Li Li-Jun, Lu Qin, Jia Yi-Fan. Preparation and characteristics of ultra-wide Ga2O3 nanoribbons up to millimeter-long level without catalyst. Acta Physica Sinica, 2020, 69(16): 168101. doi: 10.7498/aps.69.20200481 [10] Ma Teng-Yu, Li Wan-Jun, He Xian-Wang, Hu Hui, Huang Li-Juan, Zhang Hong, Xiong Yuan-Qiang, Li Hong-Lin, Ye Li-Juan, Kong Chun-Yang. Size Regulation and Photoluminescence Properties of β-Ga2O3 Nanomaterials. Acta Physica Sinica, 2020, 69(10): 108102. doi: 10.7498/aps.69.20200158 [11] Cai Cheng-Xin, Chen Shao-Geng, Wang Xue-Mei, Liang Jun-Yan, Wang Zhao-Hong. Phononic band structure and figure of merit of three-dimensional anisotropic asymmetric double-cone pentamode metamaterials. Acta Physica Sinica, 2020, 69(13): 134302. doi: 10.7498/aps.69.20200364 [12] Gu Hong-Ming, Huang Yong-Qing, Wang Huan-Huan, Wu Gang, Duan Xiao-Feng, Liu Kai, Ren Xiao-Min. Theoretical analysis of new optical microcavity. Acta Physica Sinica, 2018, 67(14): 144201. doi: 10.7498/aps.67.20180067 [13] Feng Qiu-Ju, Li Fang, Li Tong-Tong, Li Yun-Zheng, Shi Bo, Li Meng-Ke, Liang Hong-Wei. Growth and characterization of grid-like β-Ga2O3 nanowires by electric field assisted chemical vapor deposition method. Acta Physica Sinica, 2018, 67(21): 218101. doi: 10.7498/aps.67.20180805 [14] Liu Xiang-Yuan, Qian Xian-Mei, Zhang Sui-Meng, Cui Chao-Long. Numerical calculation and discussion on the return photon number of sodium laser beacon excited by a macro-micro pulse laser. Acta Physica Sinica, 2015, 64(9): 094206. doi: 10.7498/aps.64.094206 [15] Jiao Xin-Quan, Chen Jia-Bin, Wang Xiao-Li, Xue Chen-Yang, Ren Yong-Feng. Analysis of induced-transparency in an original three-order resonator system. Acta Physica Sinica, 2015, 64(14): 144202. doi: 10.7498/aps.64.144202 [16] Zheng Shu-Wen, Fan Guang-Han, He Miao, Zhao Ling-Zhi. Theoretical study of the effect of W-doping on the conductivity of β-Ga2O3. Acta Physica Sinica, 2014, 63(5): 057102. doi: 10.7498/aps.63.057102 [17] Zhang Tian-Le, Huang Xi, Zheng Kai, Zhang Xin-Wu, Wang Yu-Jie, Wu Li-Ming, Zhang Xiao-Qing, Zheng Jie, Zhu Biao. Influence of polarization voltage on piezoelectric performance of polypropylene piezoelectret films. Acta Physica Sinica, 2014, 63(15): 157703. doi: 10.7498/aps.63.157703 [18] Song Gu-Zhou, Ma Ji-Ming, Wang Kui-Lu, Zhou Ming. Analysis of figure of merit for thick pinhole imaging. Acta Physica Sinica, 2012, 61(10): 102902. doi: 10.7498/aps.61.102902 [19] Ding Yan-Hong, Li Ming-Ji, Yang Bao-He, Ma Xu. AC magnetic properties of Fe15.38Co61.52Cu0.6Nb2.5Si11B9nanocrystalline soft magnetic alloy. Acta Physica Sinica, 2011, 60(9): 097502. doi: 10.7498/aps.60.097502 [20] Ma Hai-Lin, Su Qing, Lan Wei, Liu Xue-Qin. Influence of oxygen pressure on the structure and photoluminescence of β-Ga2O3 nano-material prepared by thermal evaporation. Acta Physica Sinica, 2008, 57(11): 7322-7326. doi: 10.7498/aps.57.7322
DownLoad:
Catalog
Metrics
- Abstract views: 609
- PDF Downloads: 33
- Cited By: 0
