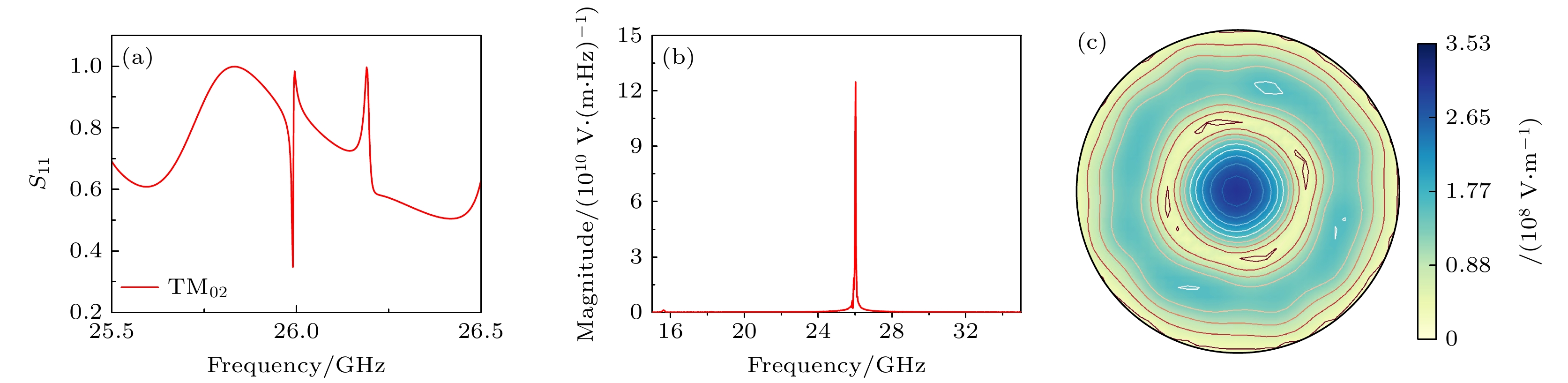
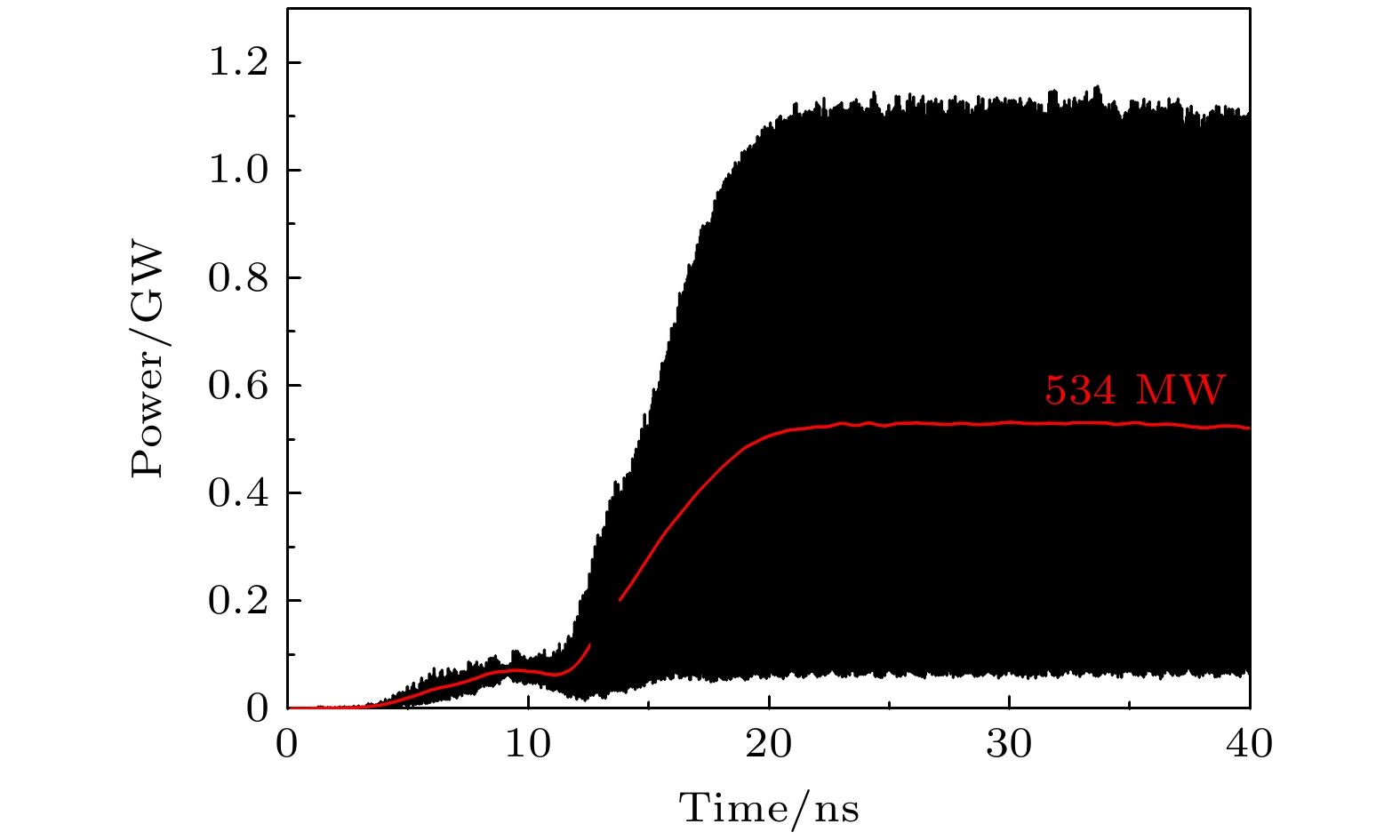
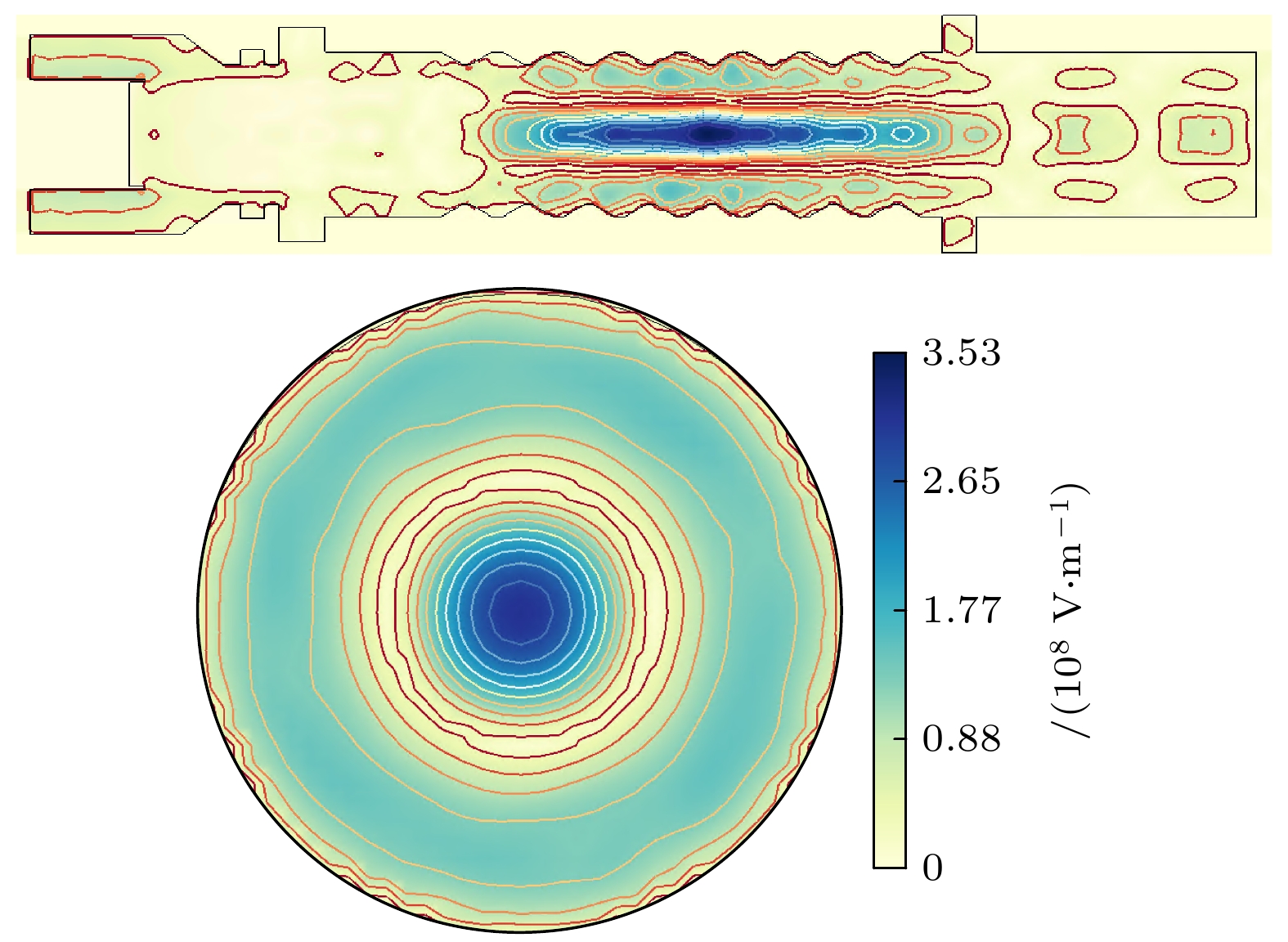
-
结合理论分析和数值模拟, 研究了TM02模过模结构相对论返波管的模式竞争机制. 理论推导得到波纹波导中混合模式与圆波导中对应模式的近似关系, 以近似模式作为波导输入来计算包含的高频结构S11参数曲线, 分析各模式的品质因数. 三维粒子模拟结果显示, 当TM02模式的耦合阻抗优势明显时, 束波作用点基本不受两端反射影响, 输出的其他模式微波主要是由互作用模式转换而来; 当耦合阻抗优势不明显时, 品质因数的改变会影响束波相互作用, 起振模式随之变化. 各模式群速度接近时, 谐振对工作模式的影响的实质是末端反射主导下的品质因数对模式的影响. 品质因数和耦合阻抗对返波管工作模式的共同作用为在输出模式稳定的前提下优化输出功率、降低磁场提供了更大空间, 使用多目标优化设计算法对相对论返波管进行优化, 最终三维模拟得到的返波管输出功率达到534 MW, TM02模式输出功率占比94.95%.
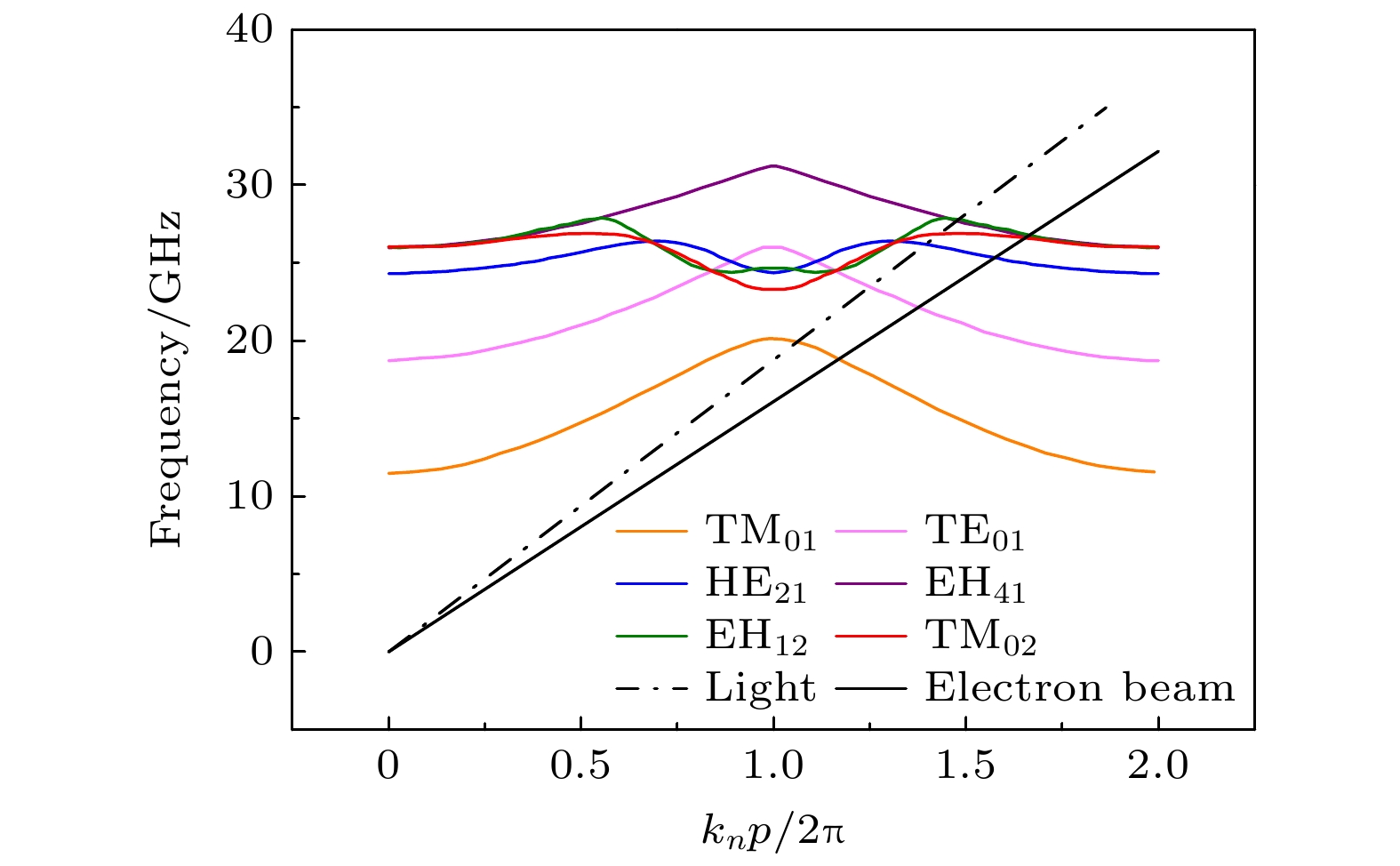
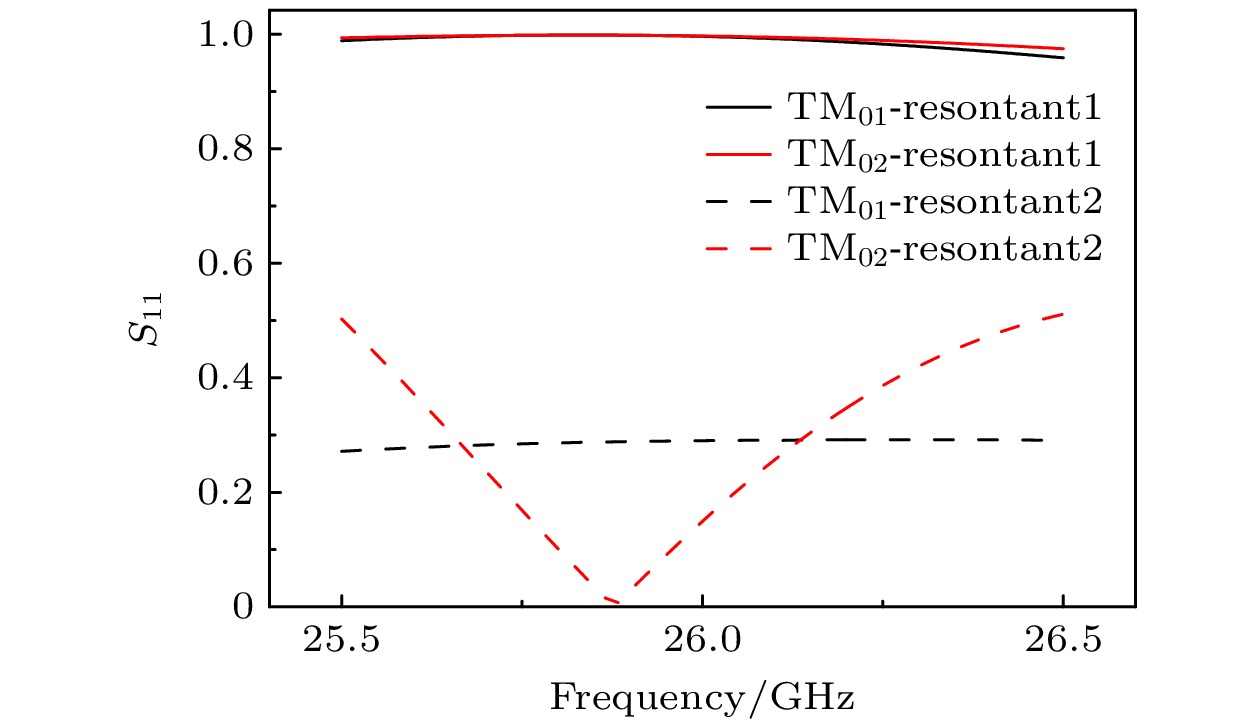
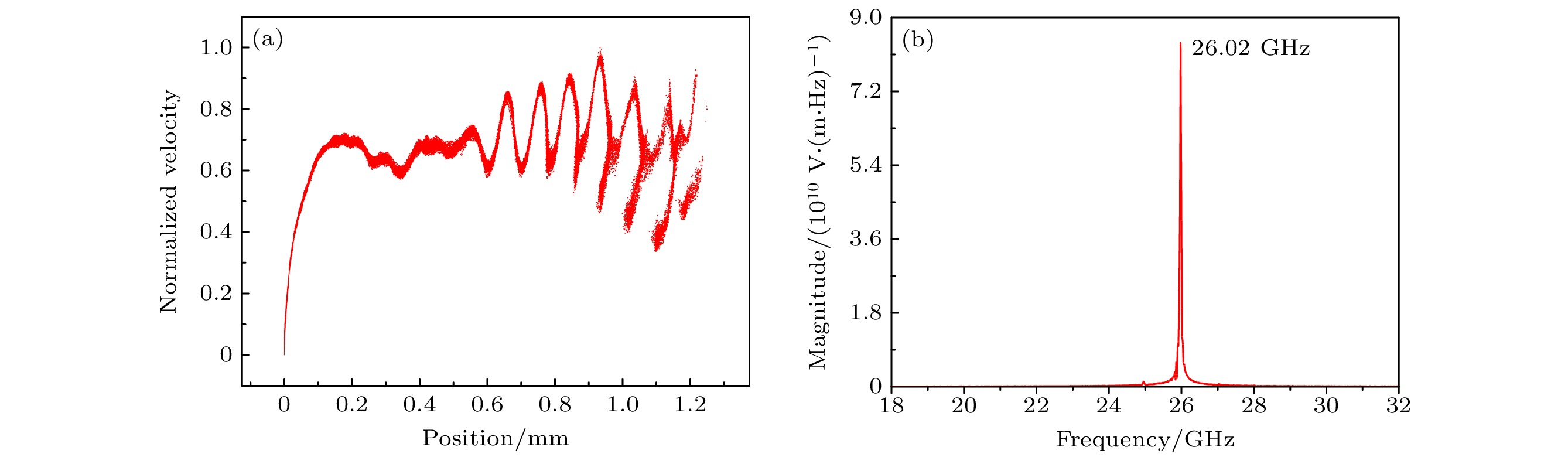
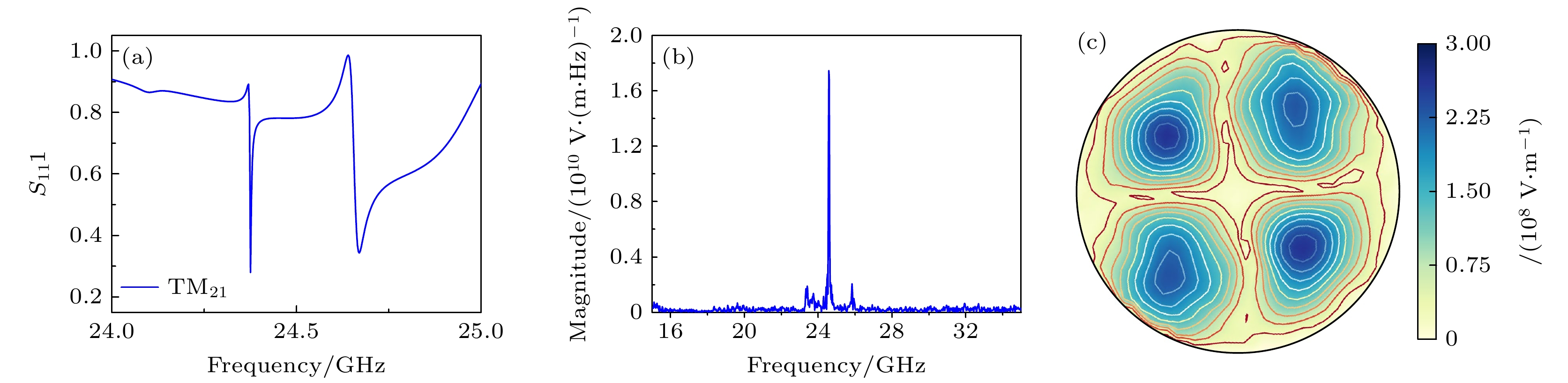
The mode competition in an overmoded relativistic backward wave oscillator is studied through theoretical analysis and three-dimensional particle-in-cell simulation in this work. Based on the quality factor and coupling impedance, the mode selection for a TM02 mode backward wave oscillator is achieved, and its output power and magnetic field strength are optimized in the simulation. The quality factor is related to the group velocity and end reflection of each mode. The dispersion curves of some non-axisymmetric modes are very close, and the group velocities are basically equal. Therefore, the end reflection needs considering to distinguish between the quality factors of different modes. In frequency domain simulation, analyzing the quality factor of each mode by using the S11 parameter curve can avoid calculating the end reflection. The three-dimensional simulation results show that the coupling impedance and quality factor jointly affect the operating mode. When the coupling impedance advantage of the working mode is not obvious, changing the resonant frequency of the high-frequency structure can affect the beam-wave interaction process, thereby changing the excitation mode. When the advantage is obvious, the beam-wave interaction of the excitation mode will not be destroyed by the resonant mode, and other modes of microwave output mainly come from the conversion of the same frequency modes. Due to the constant dispersion curve, the effect of resonance on the mode is essentially the effect of the quality factor on the mode dominated by the end reflection. The insensitive parameters and the electron beam radius obtained from the simulation are used as the optimal parameters, and the automatic optimization algorithm is used in combination with the two-dimensional simulation to perform multi-objective optimization design in the above device. The final output power of the backward wave oscillator reaches 534 MW, with an efficiency of 23.64%, an increase of 221.7% compared with the efficiency of the original device. The device operating mode remains stable, with a power ratio of TM02 mode reaching 94.95%. -
Keywords:
- relativistic backward wave oscillator /
- mode selection /
- non-axisymmetric mode /
- particle-in-cell simulation
[1] 本福德, 斯威格, 谢米洛格鲁 著 (江伟华, 张驰 译) 2009 高功率微波 (北京: 国防工业出版社) 第1, 2页
Benford J, Swegle J A, Schamiloglu E (translated by Jiang W H, Zhang C) 2009 High Power Microwave (Beijing: National Defence Industry Press) pp1, 2
[2] Gold S H, Nusinovich G S 1997 Rev. Sci. Instrum. 68 3945
Google Scholar
[3] Gunin A V, Klimov A I, Korovin S D, Kurkan I K, Pegel I V, Polevin S D, Roitman A M, Rostov V V, Stepchenko A S, Totmeninov E M 1998 IEEE Trans. Plasma Sci. 26 326
Google Scholar
[4] Ye H, Chen C H, Hui N, Teng Y 2015 IEEE International Vacuum Electronics Conference (IVEC) Beijing, China April 27–29, 2015 p15412768
[5] Xiao R Z, Shi Y C, Wang H D, Zhang G, Sun J 2020 Phys. Plasmas 27 043102
Google Scholar
[6] Teng Y, Cao Y B, Song Z M, Ye H, Shi Y C, Chen C H, Sun J 2014 Phys. Plasmas 21 123108
Google Scholar
[7] Teng Y, Wang D Y, Li S, Yang D W, Shi Y C, Wu P, Wu X 2019 Phys. Plasmas 26 053105
Google Scholar
[8] Vlasov A N, Shkvarunets A G, Rodgers J C, Carmel Y, Antonsen T M, Abuelfadl T M, Lingze D, Cherepenin V A, Nusinovich G S, Botton M 2000 IEEE Trans. Plasma Sci. 28 550
Google Scholar
[9] Zhang D, Zhang J, Zhong H H, Jin Z, Yuan Y 2014 Phys. Plasmas 21 491
Google Scholar
[10] 刘国治, 陈昌华 2021 相对论返波管导论 (北京: 科学出版社) 第90页
Liu G Z, Chen C H 2021 Introduction to Relativistic Backwave Oscillator (Beijing: Science Press) p90
[11] 张军, 钟辉煌 2005 54 206
Google Scholar
Zhang J, Zhong H H, 2005 Acta Phys. Sin. 54 206
Google Scholar
[12] Qiang L P, Teng Y, Zhang J W, Luo W, Li Y D, Wang Y, Wang H G 2022 IEEE Trans. Electron Devices 69 7025
Google Scholar
[13] 李永东, 王洪广, 刘纯亮, 张殿辉, 王建国, 王玥 2009 强激光与粒子束 21 1866
Li Y D, Wang H G, Liu C L, Zhang D H, Wang J G, Wang Y 2009 High Power Laser Part. Beams 21 1866
[14] Wang J G, Chen Z G, Wang Y, Zhang D H, Liu C L, Li Y D, Wang H G, Qiao H L, Fu M Y, Yuan Y A 2010 Phys. Plasmas 17 073107
Google Scholar
[15] Fang A P, Liang S S, Li Y D, Wang H G, Wang Y 2020 Chin. Phys. B 29 100205
Google Scholar
[16] Yang W J, Li Y D, Wang H G, Jiang M, Cao M, Liu C L 2023 IEEE Trans. Electron Devices 70 3892
Google Scholar
[17] Le Chap T 1998 An Introduction to Genetic Algorithms (Cambridge: MIT Press
[18] Chou S Y, Chang Y H, Shen C Y 2008 Eur. J. Operational Res. 189 132
Google Scholar
[19] Bugaev S P, Cherepenin V A 1990 IEEE Trans. Plasma Sci. 18 518
Google Scholar
[20] Swegle J A, Poukey J W, Leifeste G T 1985 Phys. Fluids 28 2882
Google Scholar
[21] 金建铭 著 (尹家贺 译) 2017 高等电磁场理论 (北京: 电子工业出版社) 第183—186页
Jin J M 2017 Theory and Computation of Electromagnetic Fields (2nd Ed.) (Beijing: Publishing House of Electronics Industry) pp183–186
-
图 3 色散曲线相近的各模式耦合阻抗
Fig. 3. Coupling impedance of modes with similar dispersion curves.
图 6 不同结构输出功率随阴极位置变化
Fig. 6. Variation of output power of different structures with position of cathode.
图 11 高频结构中不同模式的S11参数
Fig. 11. S11 parameters for different modes in high frequency structure
图 12 rb = 7.0 mm, L = 9 mm时的PIC模拟结果 (a) 电子相空间分布; (b) 输出频谱
Fig. 12. PIC simulation results when rb = 7.0 mm, L = 9 mm: (a) Electronic phase spatial distribution; (b) output spectrum.
图 13 rb = 7.4 mm, L = 9 mm时的PIC模拟结果 (a) 电子相空间分布; (b) 输出频谱
Fig. 13. PIC simulation results when rb = 7.4 mm, L = 9 mm: (a) Electronic phase spatial distribution; (b) output spectrum.
图 14 输出TM21模式时模拟结果 (a) S11参数; (b) 频谱; (c) 电场幅值
Fig. 14. Simulation results when TM21 mode is output: (a) S11 parameter; (b) spectrum; (c) electric field amplitude
图 16 输出TM02模式时模拟结果 (a) S11参数; (b) 频谱; (c) 电场幅值
Fig. 16. Simulation results when TM02 mode is output: (a) S11 parameter; (b) spectrum; (c) electric field amplitude.
图 15 输出TE41模式时模拟结果 (a) S11参数; (b) 频谱; (c) 电场幅值
Fig. 15. Simulation results when TE41 mode is output: (a) S11 parameter; (b) spectrum; (c) electric field amplitude.
图 17 不同输出半径下模式纯度随漂移段长度的变化
Fig. 17. Variation of the mode purity with L under different rout.
表 1 谐振腔反射器参数
Table 1. Parameters of the resontants.
序号 Lr1/mm Lr2/mm Lb/mm rr1/mm rr2/mm ra/mm rb/mm rc/mm 1 3.0 6.0 2.0 11.0 14.0 9.2 9.2 10.8 2 6.7 7.0 9.0 14.1 14.1 10.8 9.2 10.8 
下载: 导出CSV
表 2 PIC模拟结果
Table 2. PIC simulation results.
序号 L/mm rb/mm TM02功率
占比/%主要竞争模式
及占比/%1 7.0 7.0 35.27 TM01 24.36 2 7.5 7.0 42.09 TE41 27.92 3 8.0 7.0 73.69 TE01 13.91 4 8.5 7.0 33.24 TE41 30.12 5 9.0 7.0 46.75 TE41 32.53 6 10.0 7.0 53.70 TM01 19.66 7 11.0 7.0 54.95 TM01 22.72
下载: 导出CSV
表 3 L = 9 mm时不同模式功率占比与品质因数
Table 3. Power ratio and Q of different modes when L = 9 mm.
模式 TM02 TE41 TM01 TE01 其他 功率占比/% 46.75 32.53 19.09 1.52 0.01 谐振频率 f/GHz 26.00 25.98 26.09 25.95 — Q 23.32 6493.75 783.48 462.57 —
下载: 导出CSV
表 4 不同模式的工作参数
Table 4. Operating parameters.
模式 TM02 TE41 TM21 工作频率/GHz 26.02 25.83 24.57 谐振频率f/GHz 26.00 25.97 24.38 rout/mm 10.8 10.6 10.7 L/mm 9.0 11.0 7.0 Q 3610.8 3935.6 2890.6
下载: 导出CSV
表 5 参数变化范围及精度
Table 5. Parameter variation range and precision.
参数 初始值 变化范围 精度 L/mm 7.0 [5.0, 11.0] 0.1 re/mm 16.5 [14.0, 20.0] 0.1 rb/mm 7.0 [6.4, 7.6] 0.1 LB/mm 125.0 [100.0, 160.0] 0.1 B/T 2.8 [0.4, 3.0] 0.01
下载: 导出CSV
表 6 各参数优化结果
Table 6. Optimization results of each parameter.
参数 L/mm re/mm rb/mm LB/mm B/T 优化结果 6.5 15.5 7.2 118.1 1.42
下载: 导出CSV
-
[1] 本福德, 斯威格, 谢米洛格鲁 著 (江伟华, 张驰 译) 2009 高功率微波 (北京: 国防工业出版社) 第1, 2页
Benford J, Swegle J A, Schamiloglu E (translated by Jiang W H, Zhang C) 2009 High Power Microwave (Beijing: National Defence Industry Press) pp1, 2
[2] Gold S H, Nusinovich G S 1997 Rev. Sci. Instrum. 68 3945
Google Scholar
[3] Gunin A V, Klimov A I, Korovin S D, Kurkan I K, Pegel I V, Polevin S D, Roitman A M, Rostov V V, Stepchenko A S, Totmeninov E M 1998 IEEE Trans. Plasma Sci. 26 326
Google Scholar
[4] Ye H, Chen C H, Hui N, Teng Y 2015 IEEE International Vacuum Electronics Conference (IVEC) Beijing, China April 27–29, 2015 p15412768
[5] Xiao R Z, Shi Y C, Wang H D, Zhang G, Sun J 2020 Phys. Plasmas 27 043102
Google Scholar
[6] Teng Y, Cao Y B, Song Z M, Ye H, Shi Y C, Chen C H, Sun J 2014 Phys. Plasmas 21 123108
Google Scholar
[7] Teng Y, Wang D Y, Li S, Yang D W, Shi Y C, Wu P, Wu X 2019 Phys. Plasmas 26 053105
Google Scholar
[8] Vlasov A N, Shkvarunets A G, Rodgers J C, Carmel Y, Antonsen T M, Abuelfadl T M, Lingze D, Cherepenin V A, Nusinovich G S, Botton M 2000 IEEE Trans. Plasma Sci. 28 550
Google Scholar
[9] Zhang D, Zhang J, Zhong H H, Jin Z, Yuan Y 2014 Phys. Plasmas 21 491
Google Scholar
[10] 刘国治, 陈昌华 2021 相对论返波管导论 (北京: 科学出版社) 第90页
Liu G Z, Chen C H 2021 Introduction to Relativistic Backwave Oscillator (Beijing: Science Press) p90
[11] 张军, 钟辉煌 2005 54 206
Google Scholar
Zhang J, Zhong H H, 2005 Acta Phys. Sin. 54 206
Google Scholar
[12] Qiang L P, Teng Y, Zhang J W, Luo W, Li Y D, Wang Y, Wang H G 2022 IEEE Trans. Electron Devices 69 7025
Google Scholar
[13] 李永东, 王洪广, 刘纯亮, 张殿辉, 王建国, 王玥 2009 强激光与粒子束 21 1866
Li Y D, Wang H G, Liu C L, Zhang D H, Wang J G, Wang Y 2009 High Power Laser Part. Beams 21 1866
[14] Wang J G, Chen Z G, Wang Y, Zhang D H, Liu C L, Li Y D, Wang H G, Qiao H L, Fu M Y, Yuan Y A 2010 Phys. Plasmas 17 073107
Google Scholar
[15] Fang A P, Liang S S, Li Y D, Wang H G, Wang Y 2020 Chin. Phys. B 29 100205
Google Scholar
[16] Yang W J, Li Y D, Wang H G, Jiang M, Cao M, Liu C L 2023 IEEE Trans. Electron Devices 70 3892
Google Scholar
[17] Le Chap T 1998 An Introduction to Genetic Algorithms (Cambridge: MIT Press
[18] Chou S Y, Chang Y H, Shen C Y 2008 Eur. J. Operational Res. 189 132
Google Scholar
[19] Bugaev S P, Cherepenin V A 1990 IEEE Trans. Plasma Sci. 18 518
Google Scholar
[20] Swegle J A, Poukey J W, Leifeste G T 1985 Phys. Fluids 28 2882
Google Scholar
[21] 金建铭 著 (尹家贺 译) 2017 高等电磁场理论 (北京: 电子工业出版社) 第183—186页
Jin J M 2017 Theory and Computation of Electromagnetic Fields (2nd Ed.) (Beijing: Publishing House of Electronics Industry) pp183–186
下载:
计量
- 文章访问数: 2243
- PDF下载量: 65
- 被引次数: 0
