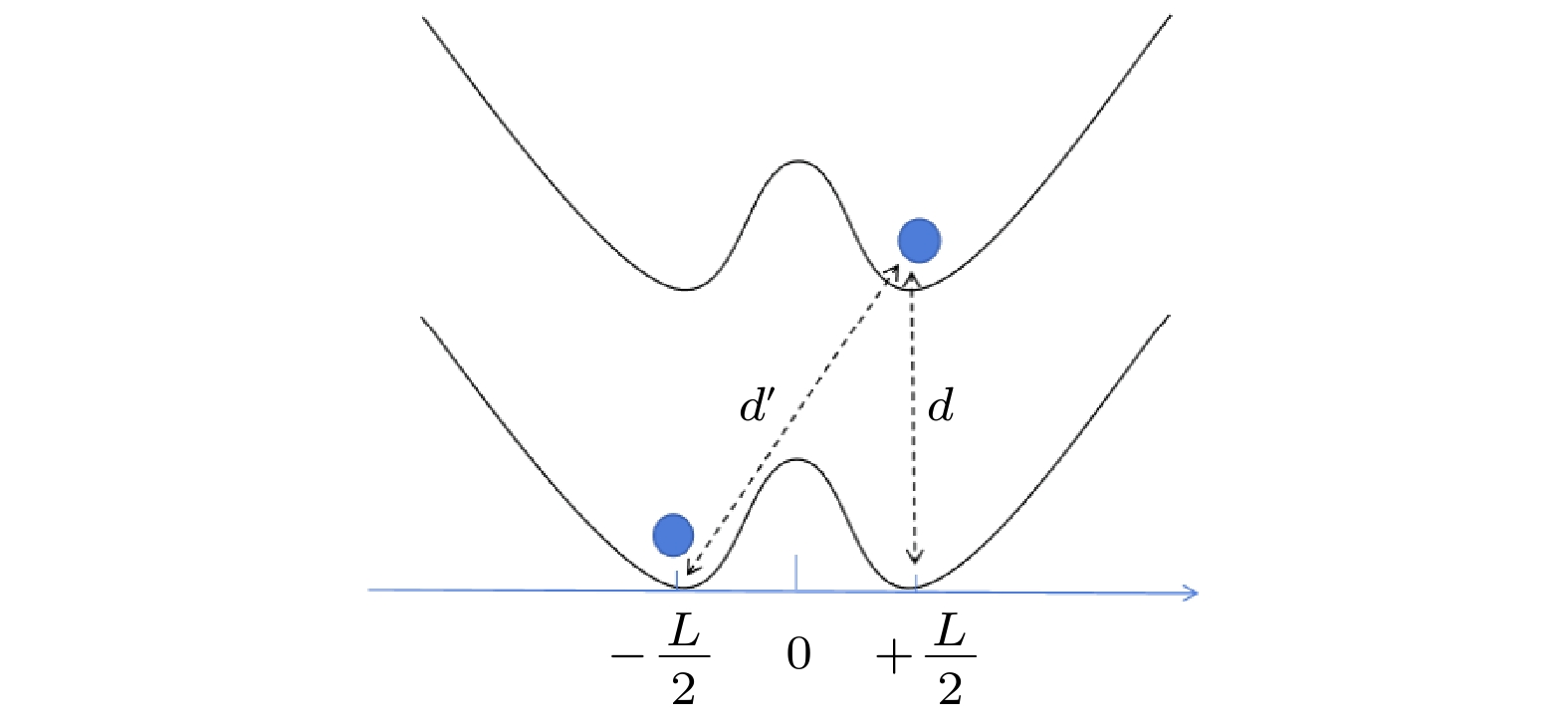
-
The exploration of the quantum nature of gravity has always been the focus of academic research. In this work, we consider a double “gravitational cat state” quantum system consisting of a pair of massive particles coupled with gravitational interaction confined in their respective double potential wells. Specifically, we model the double “gravitational cat state” system as a two-qubit system by assuming that the system is initially in the two-qubit Bell state, and investigate the effects of stable classical field and decayed field noise on the quantum speed limit time (QSLT) and trace distance discord (TDD) dynamics of the double “gravitational cat state”. The results show that the QSLT can be controlled by changing the parameters of the system and the environment, and the quantum state dynamic evolution of the system with massive particles can be accelerated. The quantum state evolution can be accelerated by increasing the gravitational coupling intensity between the two massive particles. The decay rate of the decaying field can also regulate the QSLT of the system to a certain extent, so as to accelerate the quantum state evolution. Under the influence of decaying field noise, it is worth noting that the intensity of gravitational coupling affects the frequency of quantum discord oscillations in this two-particle system. The QSLT shows an oscillating trend with time: rapidly increasing to a certain value in a short period of time, then beginning to decline, and then oscillating until it reaches a stable value. That is to say, the evolution of quantum states goes through an oscillatory cycle of first deceleration and then acceleration until the evolution rate becomes stable after a certain period of time. At the same time, there are similar oscillations in the dynamics of quantum discord. Moreover, by comparing these two, it is found that the QSLT decreases in the process of increasing the quantum discord in the system. When the discord oscillation has regularity, the QSLT tends to a certain value, and the quantum discord of the double “gravitational cat state” system has a certain relationship with the QSLT. In other words, the quantum discord will affect the rate of quantum state evolution to some extent, and the increase of quantum discord between systems will be more conducive to the evolution of quantum states.
-
Keywords:
- open system dynamics /
- quantum speed limits time /
- quantum discord /
- gravitational cat state
[1] Marletto C, Vedral V 2017 NPJ Quantum Inf. 3 41
Google Scholar
[2] Rovelli C 2021 Universe 7 439
Google Scholar
[3] Bose S, Mazumdar A, Schut M, Toroš M 2022 Phys. Rev. D 105 106028
Google Scholar
[4] Carlesso M, Bassi A, Paternostro M, Ulbricht H 2019 New J. Phys. 21 093052
Google Scholar
[5] Miki D, Matsumura A, Yamamoto K 2021 Phys. Rev. D 103 026017
Google Scholar
[6] Belenchia A, Wald R M, Giacomini F, Castro-Ruiz E, Časlav B, Aspelmeyer M 2018 Phys. Rev. D 98 126009
Google Scholar
[7] Bose S, Mazumdar A, Morley G W, Ulbricht H, Toroš M, Paternostro M, Geraci A A, Barker P F, Kim M S, Milburn G 2017 Phys. Rev. Lett. 119 240401
Google Scholar
[8] Marletto C, Vedral V 2017 Phys. Rev. Lett. 119 240402
Google Scholar
[9] Carney D, Stamp P C E, Taylor J M 2019 Classical Quantum Gravity 36 034001
Google Scholar
[10] Cataño-Lopez S B, Santiago-Condori J G, Edamatsu K, Matsumoto N 2020 Phys. Rev. Lett. 124 221102
Google Scholar
[11] Matsumoto N, Cataño-Lopez S B, Sugawara M, Suzuki S, Abe N, Komori K, Michimura Y, Aso Y, Edamatsu K 2019 Phys. Rev. Lett. 122 071101
Google Scholar
[12] Anastopoulos C, Hu B L 2020 Classical Quantum Gravity 37 235012
Google Scholar
[13] Dahbi Z, Rahman A U, Mansour M 2023 Physica A 609 128333
Google Scholar
[14] Rojas M, Lobo I P 2023 Universe 9 71
Google Scholar
[15] Hadipour M, Haseli S 2024 Europhys. Lett. 147 29003
Google Scholar
[16] Haddadi S, Ghominejad M, Czerwinski A 2024 Eur. Phys. J. C 84 670
Google Scholar
[17] Shahandeh F, Lund A P, Ralph T C 2019 Phys. Rev. A 99 052303
Google Scholar
[18] Maleki Y, Scully M O, Zheltikov A M 2021 Phys. Rev. A 104 053712
Google Scholar
[19] Giovannetti V, Lloyd S, Maccone L 2011 Nat. Photonics 5 222
Google Scholar
[20] Cruz C, Anka M F, Reis M S, Bachelard R, Santos A C 2022 Quantum Sci. Technol. 7 025020
Google Scholar
[21] Gisin N, Thew R 2007 Nat. Photonics 1 165
Google Scholar
[22] Mansour M, Dahbi Z 2020 Int. J. Theor. Phys. 59 3876
Google Scholar
[23] Montealegre J D, Paula F M, Saguia A, Sarandy M S 2013 Phys. Rev. A 87 042115
Google Scholar
[24] Paula F M, Oliveira T R D, Sarandy M S 2013 Phys. Rev. A 87 064101
Google Scholar
[25] Ciccarello F, Tufarelli T, Giovannetti V 2014 New J. Phys. 16 013038
Google Scholar
[26] Rahman A U, Liu A X, Haddadi S, Qiao C F 2023 arXiv: 2308.12536 [quant-ph]
[27] Blanes S, Casas F, Oteo J A, Ros J 2009 Phys. Rep. 470 151
Google Scholar
[28] Taddei M M, Escher B M, Davidovich L, Matos Filho R L D 2013 Phys. Rev. Lett. 110 050402
Google Scholar
[29] Deffner S, Lutz E 2013 Phys. Rev. Lett. 111 010402
Google Scholar
[30] Zhang Y J, Han W, Xia Y J, Cao J P, Fan H 2014 Sci. Rep. 4 4890
Google Scholar
[31] Henderson L, Vedral V 2001 J. Phys. A Math. Gen. 34 6899
Google Scholar
[32] Ollivier H, Zurek W H 2001 Phys. Rev. Lett. 88 017901
Google Scholar
[33] Modi K, Paterek T, Son W, Vedral V, Williamson M 2010 Phys. Rev. Lett. 104 080501
Google Scholar
[34] Dakić B, Vedral V, Brukner Č 2010 Phys. Rev. Lett. 105 190502
Google Scholar
[35] Hu M L, Hu X Y, Wang J C, Peng Y, Zhang Y R, Fan H 2018 Phys. Rep. 762 1
Google Scholar
-
图 1 双“引力猫态”的物理模型, 两个双势阱位于不同的轴上, 两平行轴之间的距离为$ d{=}\sqrt {{{d'}^2} - {L^2}} $
Figure 1. Physical model of the double “gravitational cat state”, where two double wells are located on different axes and the distance between the two parallel axes is $ d{=}\sqrt {{{d'}^2} - {L^2}} $.
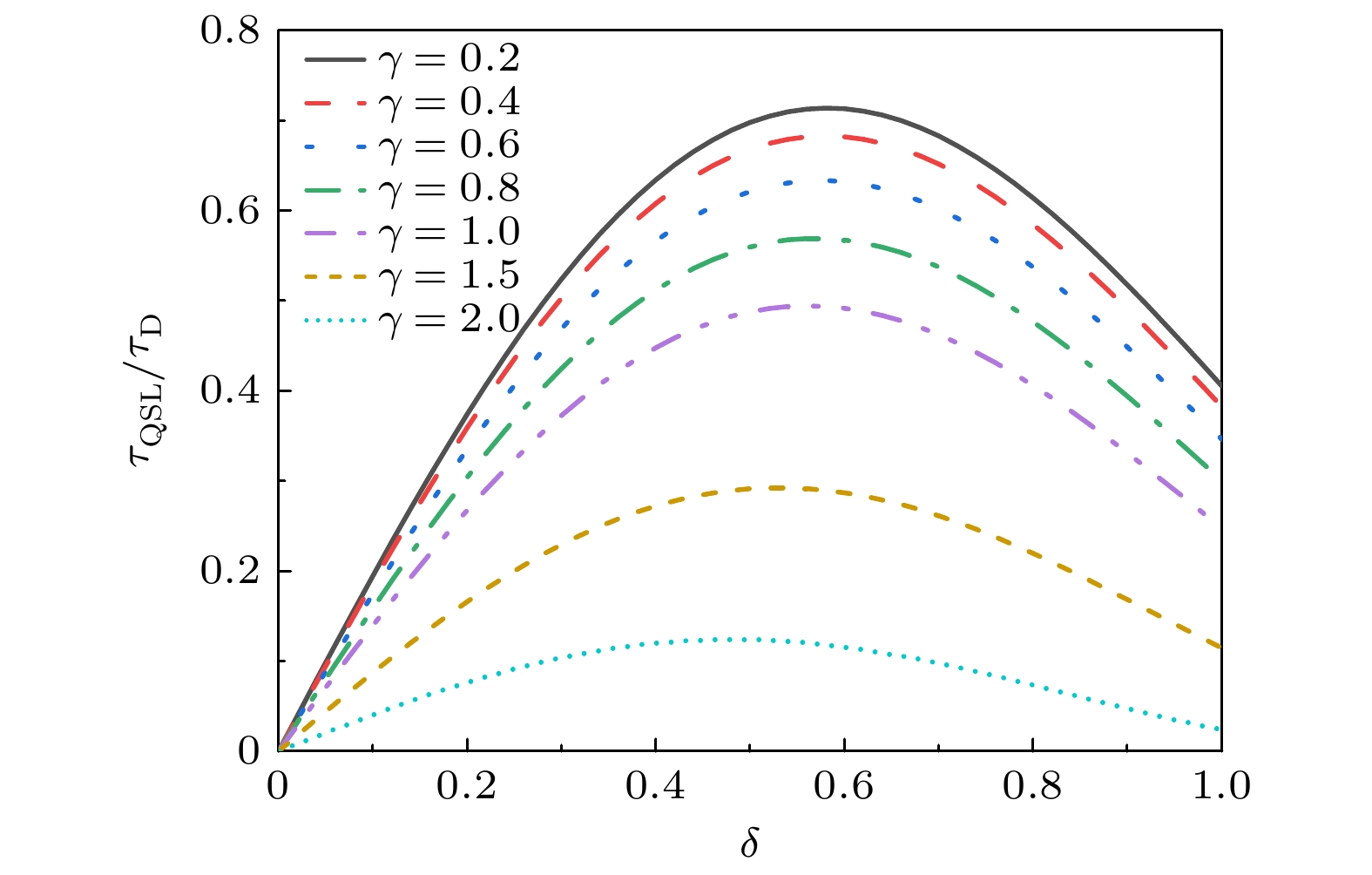
图 2 稳定经典场噪声影响下双“引力猫态” QSLT与实际演化时间的比值$ {{{\tau _{{\mathrm{QSL}}}}} {/ } {{\tau _{\mathrm{D}}}}} $随引力耦合强度$ \gamma $和经典场噪声参数$ \delta $的变化. 这里双“引力猫态”与场之间的耦合$ \lambda = 1 $, 实际演化时间$ {\tau _{\mathrm{D}}} = 1 $
Figure 2. Ratio $ {{{\tau _{{\mathrm{QSL}}}}} {/ } {{\tau _{\mathrm{D}}}}} $ of the quantum speed limit time to the actual evolution time for the double “gravitational cat state” under the influence of stable classical field noise as a function of the gravitational coupling $ \gamma $ and the parameters of the classical field noise $ \delta $. Here the coupling between the double “gravitational cat state” and the field is $ \lambda = 1 $, the evolutional time is $ {\tau _{\mathrm{D}}} = 1 $.
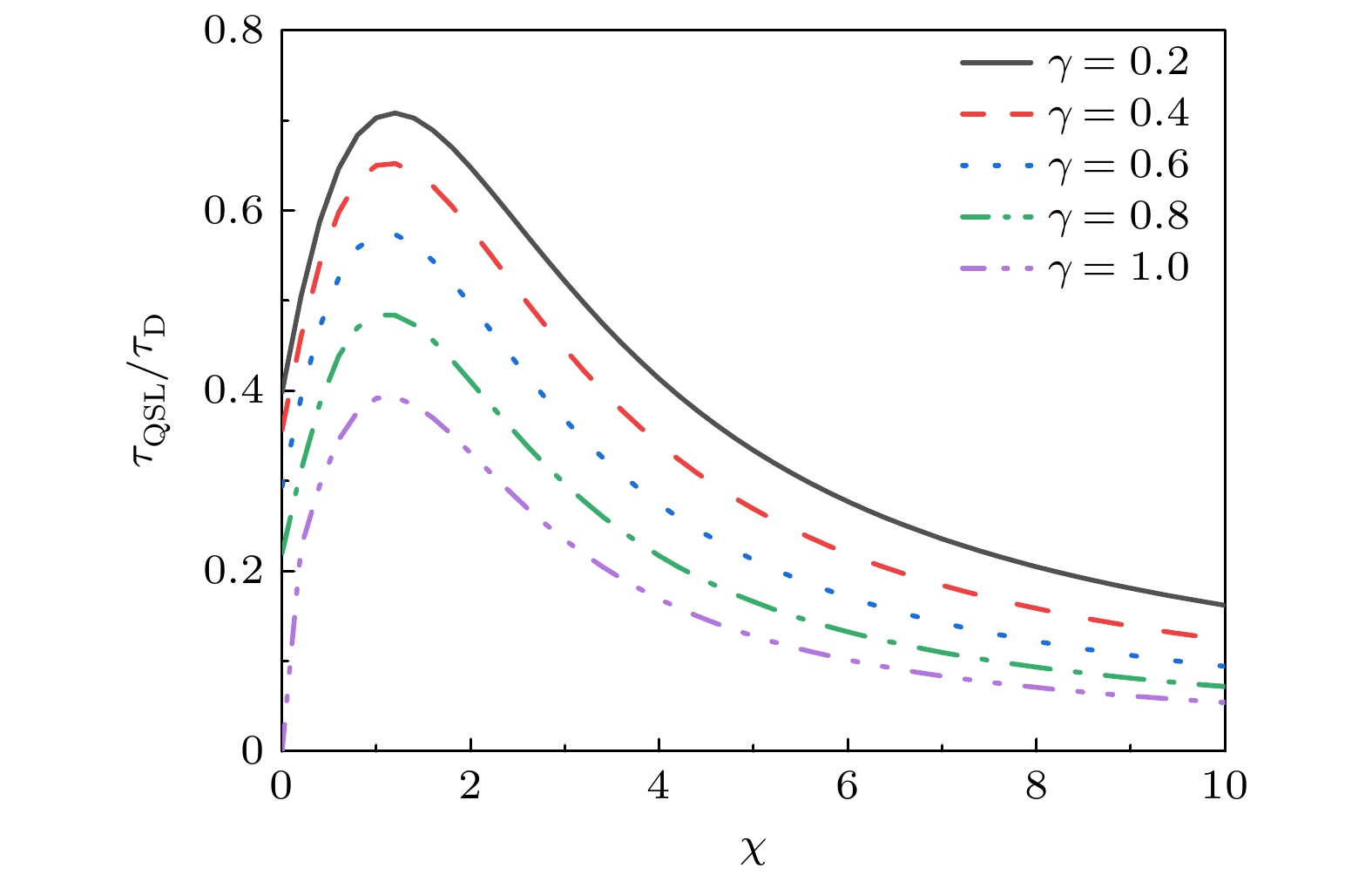
图 3 经典噪声场存在衰减时, 双“引力猫态” QSLT与实际演化时间的比值$ {{{\tau _{{\mathrm{QSL}}}}} {/ } {{\tau _{\mathrm{D}}}}} $随引力耦合强度$ \gamma $和场衰减率$ \chi $的变化. 这里$ \delta = 1 $, 双“引力猫态”与场之间的耦合$ \lambda = 1 $, 实际演化时间$ {\tau _{\mathrm{D}}} = 1 $
Figure 3. Ratio $ {{{\tau _{{\mathrm{QSL}}}}} {/ } {{\tau _{\mathrm{D}}}}} $ of the quantum speed limit time to the actual evolution time under the influence of classical decaying field for the double “gravitational cat state” as a function of the gravitational coupling $ \gamma $ and the decay rates $ \chi $. Here the coupling between the double “gravitational cat state” and the field is $ \lambda = 1 $, for $ \delta = 1 $, and the evolutional time is $ {\tau _{\mathrm{D}}} = 1 $.
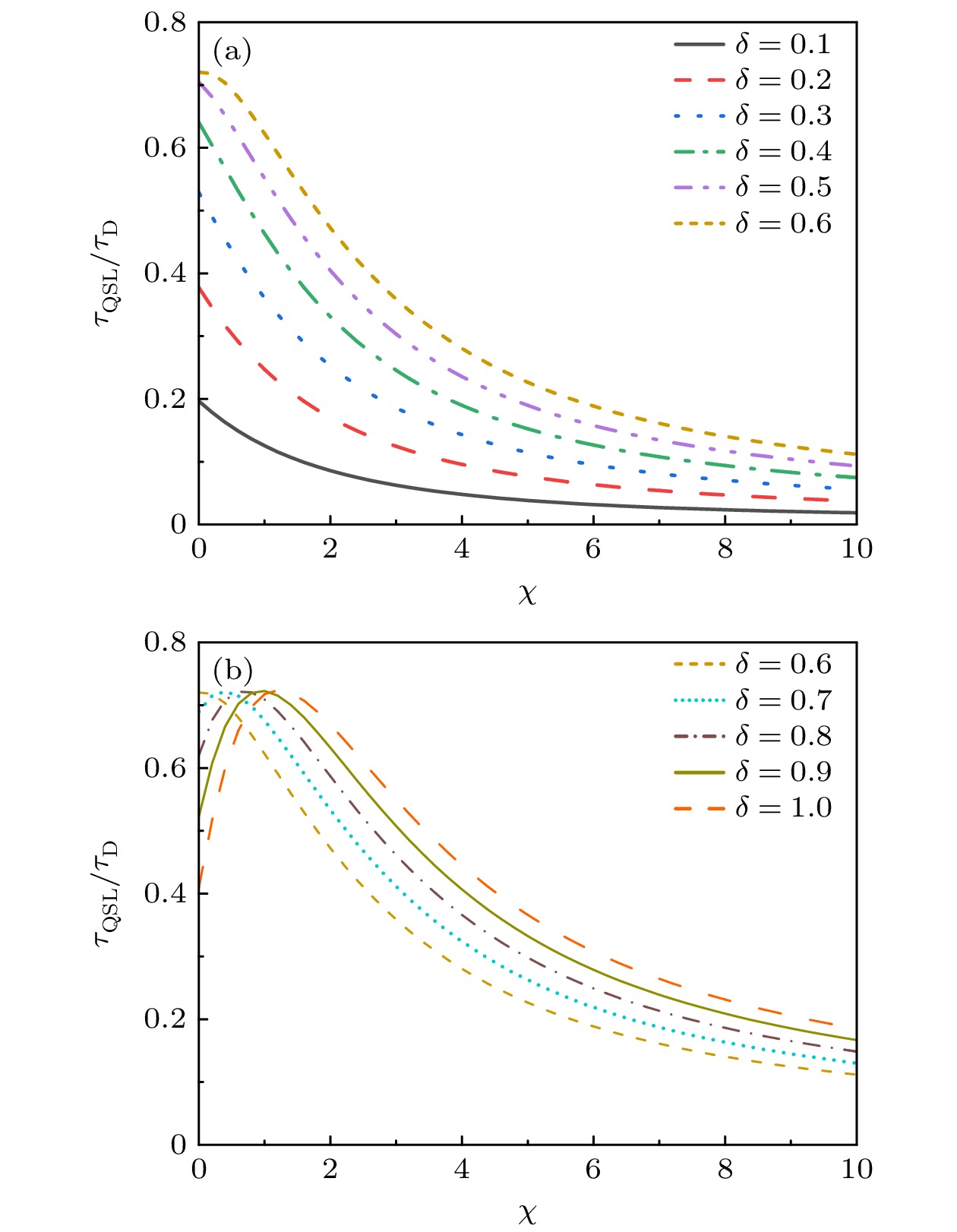
图 4 噪声场存在衰减时, 双“引力猫态”QSLT与实际演化时间的比值$ {{{\tau _{{\mathrm{QSL}}}}} {/ } {{\tau _{\mathrm{D}}}}} $随场衰减率$ \chi $和经典场参数$ \delta $的变化. 这里双“引力猫态”与场之间的耦合$ \lambda = 1 $, $ \gamma = 0.1 $, 实际演化时间$ {\tau _{\mathrm{D}}} = 1 $
Figure 4. Ratio $ {{{\tau _{{\mathrm{QSL}}}}} {/ } {{\tau _{\mathrm{D}}}}} $ of the quantum speed limit time to the actual evolution time under the influence of classical decaying field for the double “gravitational cat state” as a function of the parameters of the classical field noise $ \delta $ and the decay rates $ \chi $. Here the coupling between the double “gravitational cat state” and the field is $ \lambda = 1 $ for $ \gamma = 0.1 $, the evolutional time is $ {\tau _{\mathrm{D}}} = 1 $.
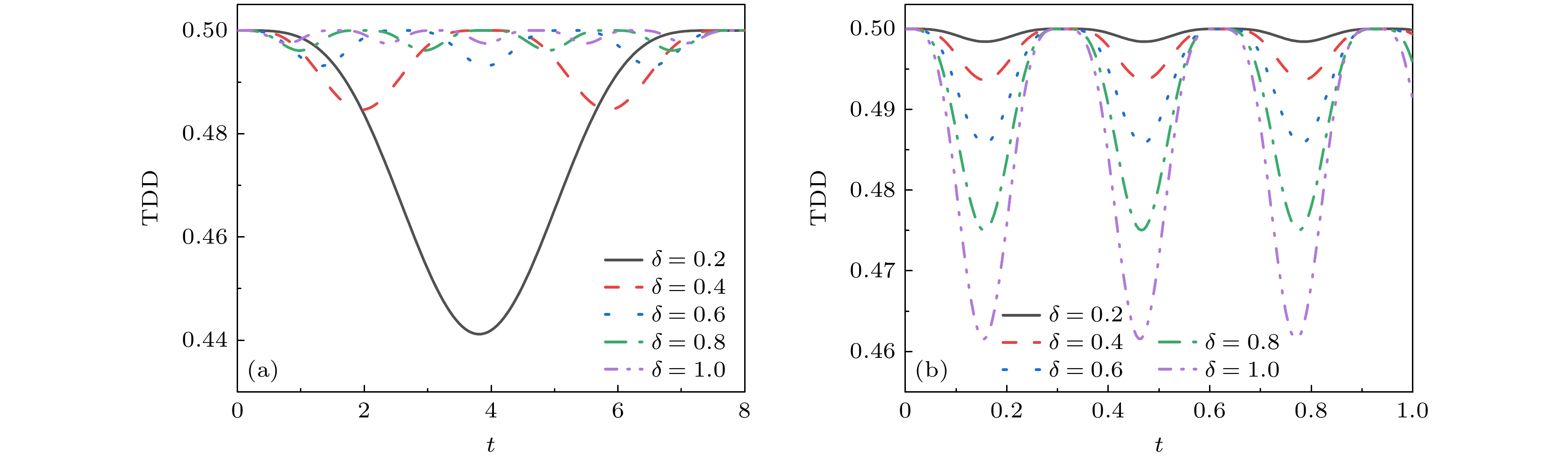
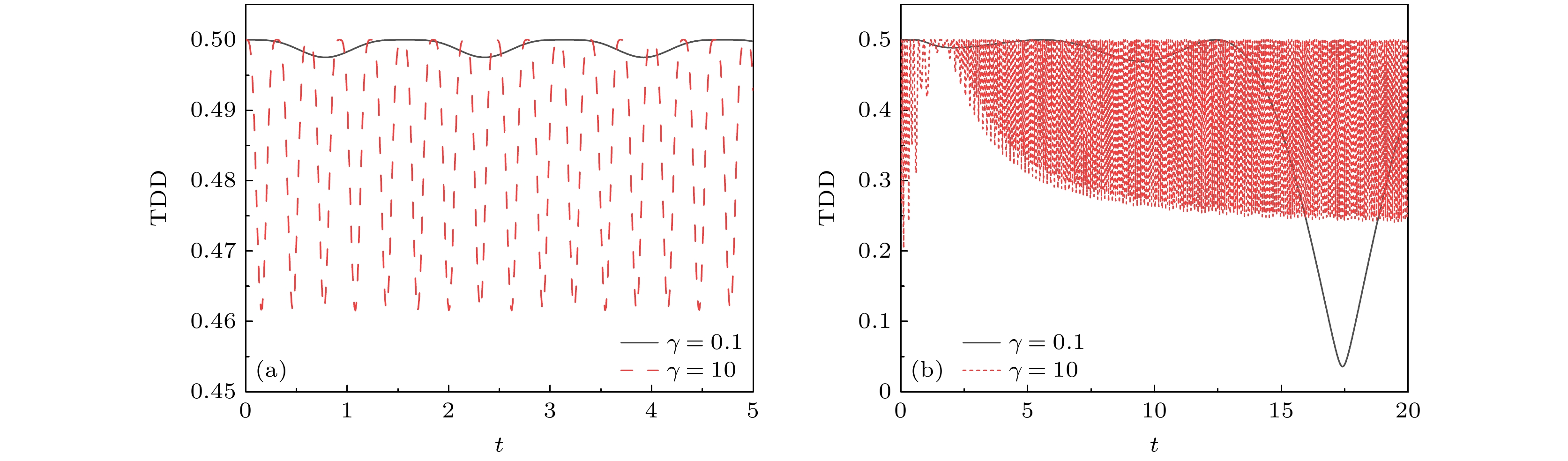
图 5 稳定经典场噪声影响下双 “引力猫态” TDD在不同的稳定经典场参数$ \delta $下随时间$ t $的变化 (a)引力耦合强度较弱时$ \gamma = 0.1 $; (b)引力耦合强度较强时$ \gamma = 10 $
Figure 5. Trace distance discord under the influence of stable classical field noise for the double “gravitational cat state” as a function of the parameters of the classical field noise $ \delta $ and evolution time $ t $: (a) The coupling between the double “gravitational cat state” is weak, for $ \gamma = 0.1 $; (b) the coupling between the double “gravitational cat state” is strong, for $ \gamma = 10 $.
图 6 在强耦合和弱耦合时, 双 “引力猫态”TDD随时间的变化, 此时$ \delta = 1 $ (a)经典场噪声影响下; (b)噪声场存在衰减, $ \chi = 1 $
Figure 6. Trace distance discord under different coupling strength for the double “gravitational cat state” as a function of the evolution time $ t $, and $ \delta = 1 $: (a) Classical field noise; (b) general local decaying field, $ \chi = 1 $.
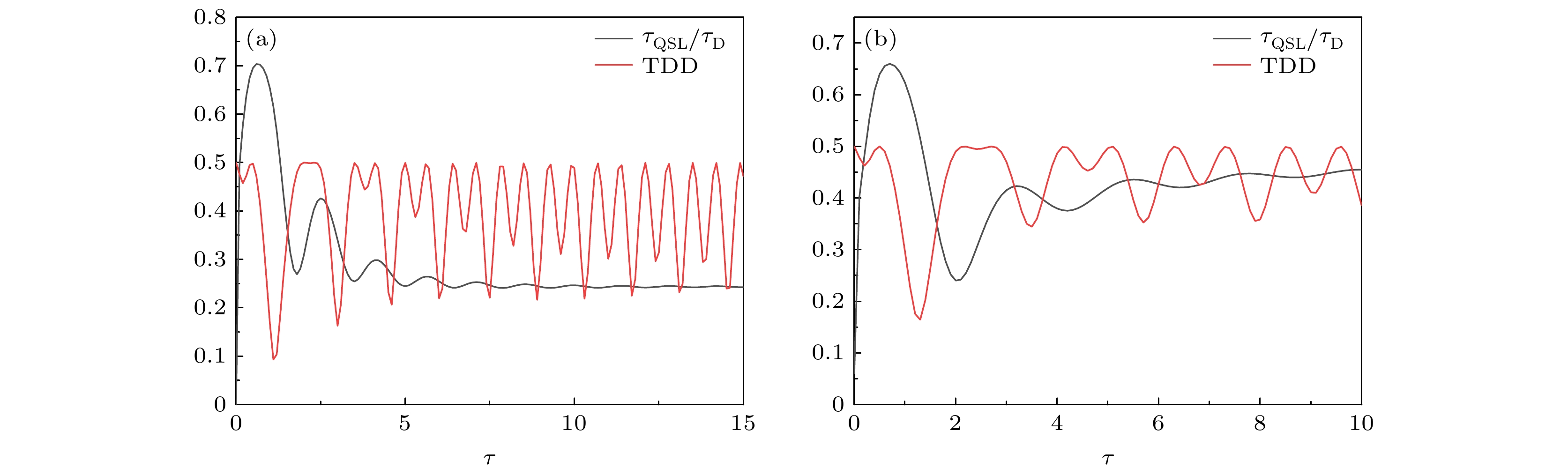
图 7 噪声场存在衰减时, 双“引力猫态” TDD和QSLT与实际演化时间的比值$ {{{\tau _{{\mathrm{QSL}}}}} {/ } {{\tau _{\mathrm{D}}}}} $作为初始时间的函数. 驱动时间$ {\tau _{\mathrm{D}}} = 1 $, $ \gamma = 1 $ (a) $ \chi = 1 $; (b) $ \chi = 2 $
Figure 7. Trace distance discord and the ratio $ {{{\tau _{{\mathrm{QSL}}}}} {/ } {{\tau _{\mathrm{D}}}}} $ of the quantum speed limit time to the actual evolution time under the influence of classical decaying field for the double “gravitational cat state” as a function of the initial evolution time $ t $, for $ {\tau _{\mathrm{D}}} = 1 $, $ \gamma = 1 $: (a) $ \chi = 1 $; (b) $ \chi = 2 $.
-
[1] Marletto C, Vedral V 2017 NPJ Quantum Inf. 3 41
Google Scholar
[2] Rovelli C 2021 Universe 7 439
Google Scholar
[3] Bose S, Mazumdar A, Schut M, Toroš M 2022 Phys. Rev. D 105 106028
Google Scholar
[4] Carlesso M, Bassi A, Paternostro M, Ulbricht H 2019 New J. Phys. 21 093052
Google Scholar
[5] Miki D, Matsumura A, Yamamoto K 2021 Phys. Rev. D 103 026017
Google Scholar
[6] Belenchia A, Wald R M, Giacomini F, Castro-Ruiz E, Časlav B, Aspelmeyer M 2018 Phys. Rev. D 98 126009
Google Scholar
[7] Bose S, Mazumdar A, Morley G W, Ulbricht H, Toroš M, Paternostro M, Geraci A A, Barker P F, Kim M S, Milburn G 2017 Phys. Rev. Lett. 119 240401
Google Scholar
[8] Marletto C, Vedral V 2017 Phys. Rev. Lett. 119 240402
Google Scholar
[9] Carney D, Stamp P C E, Taylor J M 2019 Classical Quantum Gravity 36 034001
Google Scholar
[10] Cataño-Lopez S B, Santiago-Condori J G, Edamatsu K, Matsumoto N 2020 Phys. Rev. Lett. 124 221102
Google Scholar
[11] Matsumoto N, Cataño-Lopez S B, Sugawara M, Suzuki S, Abe N, Komori K, Michimura Y, Aso Y, Edamatsu K 2019 Phys. Rev. Lett. 122 071101
Google Scholar
[12] Anastopoulos C, Hu B L 2020 Classical Quantum Gravity 37 235012
Google Scholar
[13] Dahbi Z, Rahman A U, Mansour M 2023 Physica A 609 128333
Google Scholar
[14] Rojas M, Lobo I P 2023 Universe 9 71
Google Scholar
[15] Hadipour M, Haseli S 2024 Europhys. Lett. 147 29003
Google Scholar
[16] Haddadi S, Ghominejad M, Czerwinski A 2024 Eur. Phys. J. C 84 670
Google Scholar
[17] Shahandeh F, Lund A P, Ralph T C 2019 Phys. Rev. A 99 052303
Google Scholar
[18] Maleki Y, Scully M O, Zheltikov A M 2021 Phys. Rev. A 104 053712
Google Scholar
[19] Giovannetti V, Lloyd S, Maccone L 2011 Nat. Photonics 5 222
Google Scholar
[20] Cruz C, Anka M F, Reis M S, Bachelard R, Santos A C 2022 Quantum Sci. Technol. 7 025020
Google Scholar
[21] Gisin N, Thew R 2007 Nat. Photonics 1 165
Google Scholar
[22] Mansour M, Dahbi Z 2020 Int. J. Theor. Phys. 59 3876
Google Scholar
[23] Montealegre J D, Paula F M, Saguia A, Sarandy M S 2013 Phys. Rev. A 87 042115
Google Scholar
[24] Paula F M, Oliveira T R D, Sarandy M S 2013 Phys. Rev. A 87 064101
Google Scholar
[25] Ciccarello F, Tufarelli T, Giovannetti V 2014 New J. Phys. 16 013038
Google Scholar
[26] Rahman A U, Liu A X, Haddadi S, Qiao C F 2023 arXiv: 2308.12536 [quant-ph]
[27] Blanes S, Casas F, Oteo J A, Ros J 2009 Phys. Rep. 470 151
Google Scholar
[28] Taddei M M, Escher B M, Davidovich L, Matos Filho R L D 2013 Phys. Rev. Lett. 110 050402
Google Scholar
[29] Deffner S, Lutz E 2013 Phys. Rev. Lett. 111 010402
Google Scholar
[30] Zhang Y J, Han W, Xia Y J, Cao J P, Fan H 2014 Sci. Rep. 4 4890
Google Scholar
[31] Henderson L, Vedral V 2001 J. Phys. A Math. Gen. 34 6899
Google Scholar
[32] Ollivier H, Zurek W H 2001 Phys. Rev. Lett. 88 017901
Google Scholar
[33] Modi K, Paterek T, Son W, Vedral V, Williamson M 2010 Phys. Rev. Lett. 104 080501
Google Scholar
[34] Dakić B, Vedral V, Brukner Č 2010 Phys. Rev. Lett. 105 190502
Google Scholar
[35] Hu M L, Hu X Y, Wang J C, Peng Y, Zhang Y R, Fan H 2018 Phys. Rep. 762 1
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 530
- PDF Downloads: 16
- Cited By: 0
