-
Permutation time irreversibility is an important method to quantify the nonequilibrium characteristics; however, ordinal pattern is a coarse-graining alternative of temporal structure and cannot accurately represent detailed structural information. In this paper, a fuzzy permutation time irreversibility (fpTIR) is proposed by measuring the difference between vector elements based on a negative exponential function. Amplitude permutation of vector is constructed and its membership degree is calculated, then the difference in probability distribution between the forward sequence and backward sequence is measured for fpTIR. For comparison, Shannon entropy is calculated as the average amount of information in the fuzzy permutation probability distribution, i.e. fuzzy permutation entropy (fPEn), to measure the complexity of the system. According to the surrogate theory, mode series are generated by logistic, Henon, and first-order autoregressive systems to verify the fpTIR, which is then used to analyze heart rates of congestive heart failure, healthy elderly and healthy young subjects from PhysioNet database. The results suggest that fpTIR effectively measures the nonequilibrium characteristic of system and improves the accuracy of heart rate analysis. Since fpTIR and fPEn are different in analyzing probability distributions, they have discrepancies in chaotic series and even opposite results in the heart rate signals, where the results of fpTIR are consistent with theory of complexity loss in aging and disease. In conclusion, the fpTIR not only accurately characterizes the structure of sequences and enhances the effect of the nonequilibrium analysis of complex systems, but also provides a new perspective and theoretical basis for exploring complex systems from the perspectives of nonequilibrium dynamics and entropy complexity.
-
Keywords:
- fuzzy permutation /
- time irreversibility /
- permutation entropy /
- complex system /
- symbolic dynamics
[1] Yao W P 2024 Phys. Rev. E 109 054104
Google Scholar
[2] Daw C, Finney C, Tracy E 2003 Rev. Sci. Instrum. 74 915
Google Scholar
[3] Bandt C, Pompe B 2002 Phys. Rev. Lett. 88 174102
Google Scholar
[4] Martinez J, Herrera D J, Chavez M 2018 Chaos 28 123111
Google Scholar
[5] Zanin M, Rodriguez A, Menasalvas R E, Papo D 2018 Entropy 20 665
Google Scholar
[6] Zanin M 2021 Chaos 31 103118
Google Scholar
[7] Yao W P, Dai J F, Perc M, Wang J, Yao D Z, Guo D Q 2020 Nonlinear Dyn. 100 907
Google Scholar
[8] Yao W P, Yao W L, Xu R, Wang J 2023 Commun. Nonlinear Sci. Numer. Simul. 117 106925
Google Scholar
[9] Yao W P, Yao W L, Wang J 2022 Phys. Lett. A 430 127977
Google Scholar
[10] Amigo J M, Zambrano S, Sanjuan M A 2010 Int. J. Bifurcation Chaos 20 2915
Google Scholar
[11] Amigo J M, Zambrano S, Sanjuan M A 2007 EPL 79 50001
Google Scholar
[12] Amigo J M, Kennel M B 2007 Physica D 231 137
Google Scholar
[13] Zanin M 2008 Chaos 18 013119
Google Scholar
[14] Kulp C W, Zunino L, Osborne T, Zawadzki B 2017 Phys. Rev. E 96 022218
Google Scholar
[15] Yao W P, Yao W L, Wang J, Dai J 2019 Phys. Lett. A 383 738
Google Scholar
[16] Yao W P, Yao W L, Yao D Z, Guo D Q, Wang J 2020 Appl. Phys. Lett. 116 014101
Google Scholar
[17] Yao W P, Yao W L, Wang J 2019 Phys. Lett. A 383 1764
Google Scholar
[18] Bian C, Qin C, Ma Q, Shen Q 2012 Phys. Rev. E 85 021906
Google Scholar
[19] Zunino L, Olivares F, Scholkmann F, Rosso O A 2017 Phys. Lett. A 381 1883
Google Scholar
[20] Cuesta F D, Varela E M, Molina P A, Vargas B 2018 Complexity 2018 1324696
Google Scholar
[21] Weiss G 1975 J. Appl. Probab. 12 831
Google Scholar
[22] Kelly F P 1979 Reversibility and Stochastic Networks (Chichester: Cambridge University Press) pp5–10
[23] Zadeh L A 1999 Fuzzy Sets Syst. 100 9
Google Scholar
[24] Chen W, Wang Z, Xie H B, Yu W X 2007 IEEE Trans. Neural Syst. Rehabil. Eng. 15 266
Google Scholar
[25] Rostaghi M, Khatibi M M, Ashory M R, Azami H 2021 IEEE Trans. Fuzzy Syst. 30 3785
Google Scholar
[26] 姚文坡, 刘铁兵, 戴加飞, 王俊 2014 63 078704
Google Scholar
Yao W P, Liu T B, Dai J F, Wang J 2014 Acta Phys. Sin. 63 078704
Google Scholar
[27] Schreiber T, Schmitz A 1996 Phys. Rev. Lett. 77 635
Google Scholar
[28] Schreiber T, Schmitz A 2000 Physica D 142 346
Google Scholar
[29] Goldberger A L, Amaral L A, Glass L, Hausdorff J M, Ivanov P C, Mark R G, Peng C, Stanley H E 2000 Circulation 101 e215
Google Scholar
[30] Baim D S, Colucci W S, Monrad E S, Smith, Harton S, Braunwald E 1986 J. Am. Coll. Cardiol. 7 661
Google Scholar
[31] Iyengar N, Peng C K, Morin R, Goldberger A L, Lipsitz L A 1996 Am. J. Physiol. 271 R1078
Google Scholar
[32] Goldberger A L, Peng C K, Lipsitz L A 2002 Neurobiol. Aging 23 23
Google Scholar
[33] Xiong W, Faes L, Ivanov P 2017 Phys. Rev. E 95 062114
Google Scholar
-
图 1 模糊排列时间不可逆的流程图
Figure 1. Flowchart of fuzzy permutation time irreversibility.
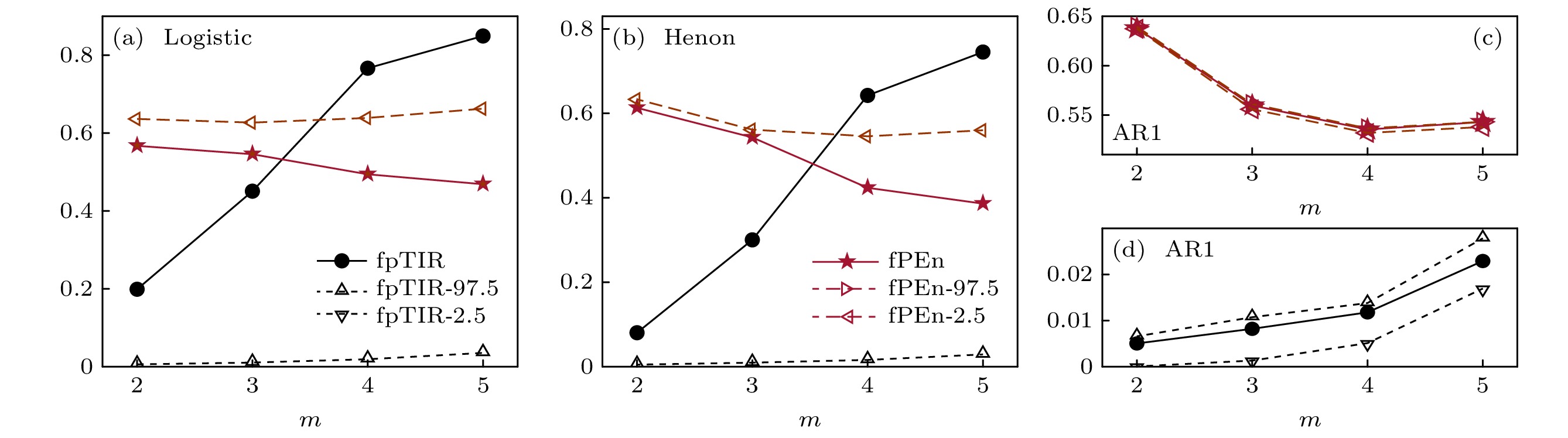
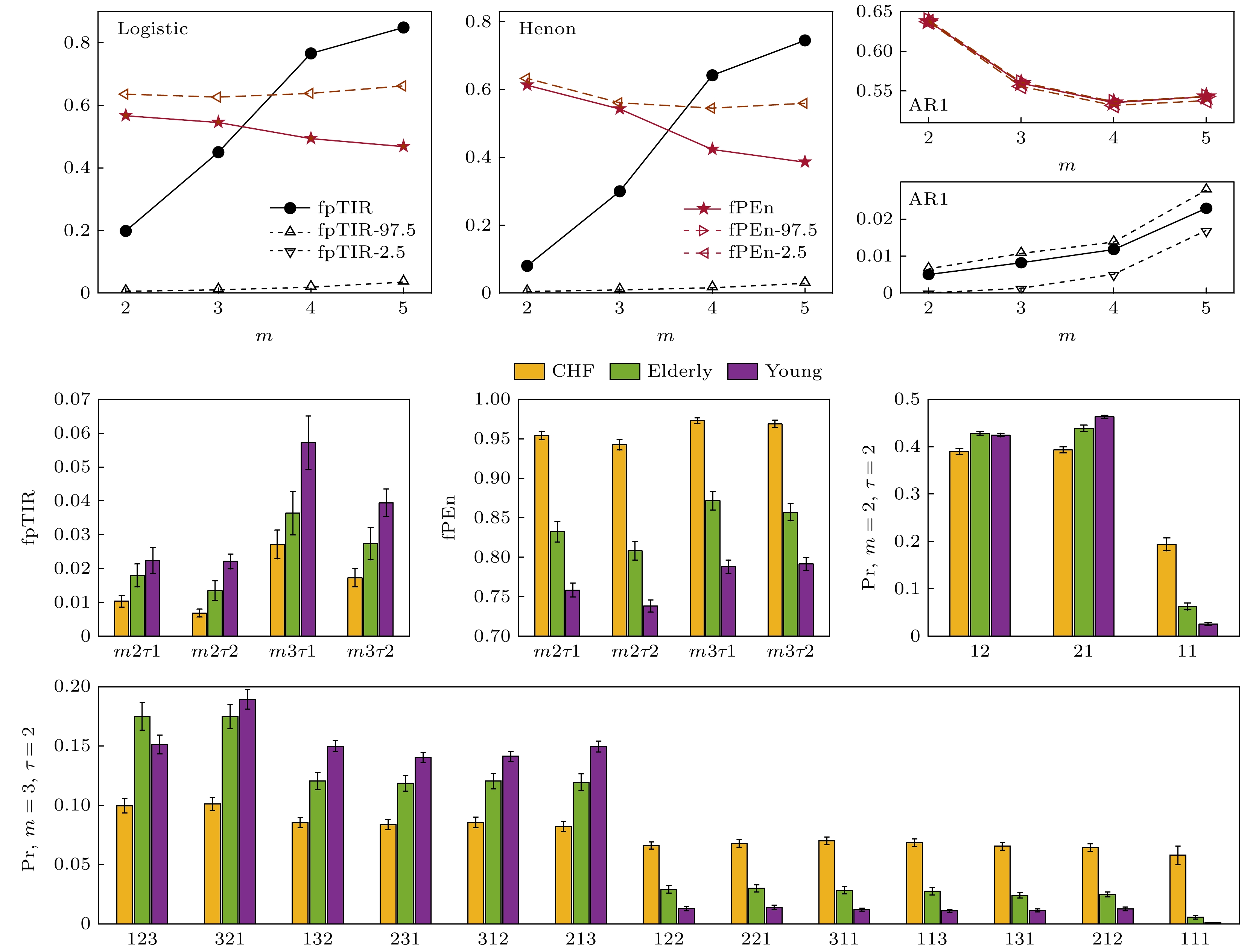
图 2 Logistic, Henon和AR1模型序列及其代替数据的fpTIR和fPEn. 隶属度控制参数$ \alpha $= 1, 向量重构参数为$ m $ = 2—5, $ \tau $ = 1. 图中fpTIR-97.5, fpTIR-2.5, fPEn-97.5和fPEn-2.5分别表示代替数据fpTIR和fPEn的97.5%和2.5%分位数
Figure 2. The fpTIR and fPEn of the logistic, Henon, and AR1 series and their surrogates. Control parameter of membership degree is $ \alpha $ = 1, dimension and delay are $ m $ = 2–5, $ \tau $ = 1. The fpTIR-97.5, fpTIR-2.5, fPEn-97.5 and fPEn-2.5 denote the 97.5% and 2.5% of fpTIR and fPEn of surrogate data.
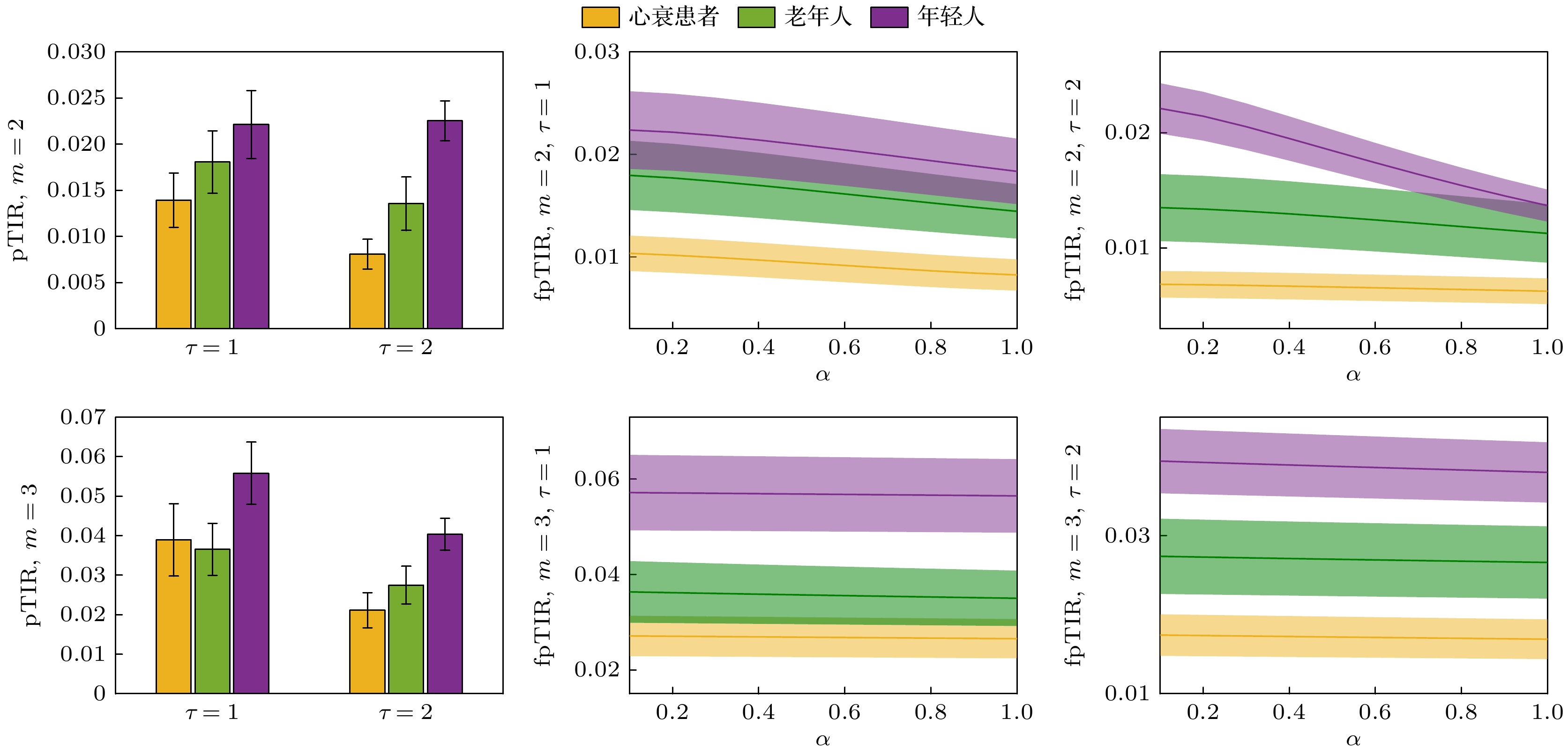
图 3 心衰、健康老年和健康年轻心率的fpTIR和pTIR (均值±标准误差), 幅度排列构建维度$ m $ = 2和3、延迟$ \tau $ = 1和2, 模糊排列隶属度$ \alpha $ = 0.1—1 (步长0.1)
Figure 3. The fpTIR and pTIR (mean ± standard error) of the CHF, healthy elderly, and healthy young heartbeats, dimension and delay of amplitude permutations are $ m $ = 2 and 3, $ \tau $ = 1 and 2, $ \alpha$= 0.1–1 with step size of 0.1.
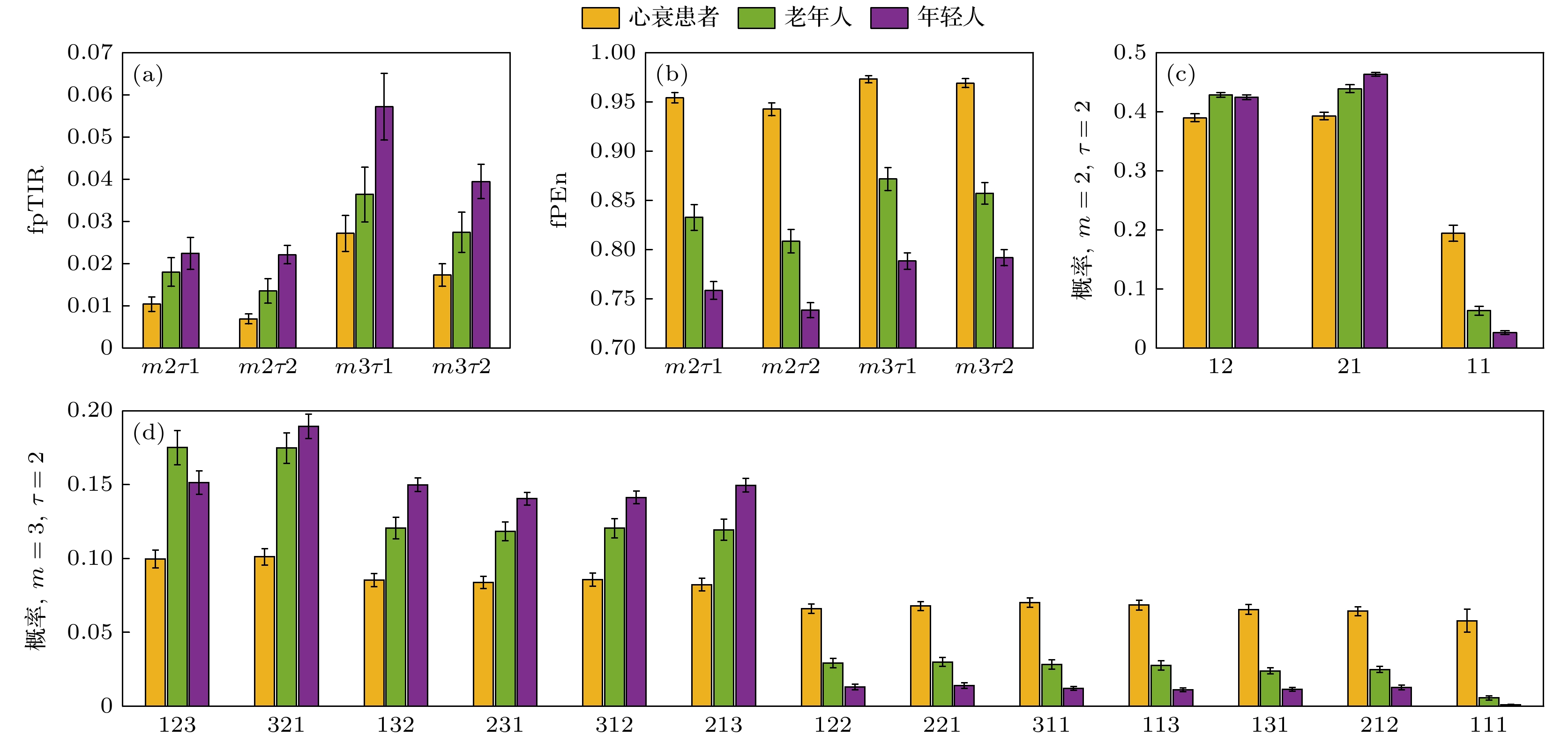
图 4 心衰、健康老年和健康年轻心率的fpTIR、fPEn和排列概率分布(均值±标准误差), 模糊排列隶属度$ \alpha $ = 0.1 (a), (b) $ m2\tau 1$表示幅度排列维度2、延迟1, 并以此类推; (c), (d) 幅度排列的维度和延迟为$ m $ = 2, $ \tau $ = 2和$ m $ = 3, $ \tau $ = 2
Figure 4. The fpTIR, pTIR and probabilities of permutations (mean ± standard error) of the CHF, healthy elderly, and healthy young heartbeats, in membership degree of amplitude permutations, $ \alpha $ = 0.1: (a), (b) $m2\tau1$ represents dimension of 2 and delay of 1, and so on; (c), (d) dimension and delay of amplitude permutations are $ m $ = 2, $ \tau $ = 2 and $ m $ = 3, $ \tau $ = 2.
-
[1] Yao W P 2024 Phys. Rev. E 109 054104
Google Scholar
[2] Daw C, Finney C, Tracy E 2003 Rev. Sci. Instrum. 74 915
Google Scholar
[3] Bandt C, Pompe B 2002 Phys. Rev. Lett. 88 174102
Google Scholar
[4] Martinez J, Herrera D J, Chavez M 2018 Chaos 28 123111
Google Scholar
[5] Zanin M, Rodriguez A, Menasalvas R E, Papo D 2018 Entropy 20 665
Google Scholar
[6] Zanin M 2021 Chaos 31 103118
Google Scholar
[7] Yao W P, Dai J F, Perc M, Wang J, Yao D Z, Guo D Q 2020 Nonlinear Dyn. 100 907
Google Scholar
[8] Yao W P, Yao W L, Xu R, Wang J 2023 Commun. Nonlinear Sci. Numer. Simul. 117 106925
Google Scholar
[9] Yao W P, Yao W L, Wang J 2022 Phys. Lett. A 430 127977
Google Scholar
[10] Amigo J M, Zambrano S, Sanjuan M A 2010 Int. J. Bifurcation Chaos 20 2915
Google Scholar
[11] Amigo J M, Zambrano S, Sanjuan M A 2007 EPL 79 50001
Google Scholar
[12] Amigo J M, Kennel M B 2007 Physica D 231 137
Google Scholar
[13] Zanin M 2008 Chaos 18 013119
Google Scholar
[14] Kulp C W, Zunino L, Osborne T, Zawadzki B 2017 Phys. Rev. E 96 022218
Google Scholar
[15] Yao W P, Yao W L, Wang J, Dai J 2019 Phys. Lett. A 383 738
Google Scholar
[16] Yao W P, Yao W L, Yao D Z, Guo D Q, Wang J 2020 Appl. Phys. Lett. 116 014101
Google Scholar
[17] Yao W P, Yao W L, Wang J 2019 Phys. Lett. A 383 1764
Google Scholar
[18] Bian C, Qin C, Ma Q, Shen Q 2012 Phys. Rev. E 85 021906
Google Scholar
[19] Zunino L, Olivares F, Scholkmann F, Rosso O A 2017 Phys. Lett. A 381 1883
Google Scholar
[20] Cuesta F D, Varela E M, Molina P A, Vargas B 2018 Complexity 2018 1324696
Google Scholar
[21] Weiss G 1975 J. Appl. Probab. 12 831
Google Scholar
[22] Kelly F P 1979 Reversibility and Stochastic Networks (Chichester: Cambridge University Press) pp5–10
[23] Zadeh L A 1999 Fuzzy Sets Syst. 100 9
Google Scholar
[24] Chen W, Wang Z, Xie H B, Yu W X 2007 IEEE Trans. Neural Syst. Rehabil. Eng. 15 266
Google Scholar
[25] Rostaghi M, Khatibi M M, Ashory M R, Azami H 2021 IEEE Trans. Fuzzy Syst. 30 3785
Google Scholar
[26] 姚文坡, 刘铁兵, 戴加飞, 王俊 2014 63 078704
Google Scholar
Yao W P, Liu T B, Dai J F, Wang J 2014 Acta Phys. Sin. 63 078704
Google Scholar
[27] Schreiber T, Schmitz A 1996 Phys. Rev. Lett. 77 635
Google Scholar
[28] Schreiber T, Schmitz A 2000 Physica D 142 346
Google Scholar
[29] Goldberger A L, Amaral L A, Glass L, Hausdorff J M, Ivanov P C, Mark R G, Peng C, Stanley H E 2000 Circulation 101 e215
Google Scholar
[30] Baim D S, Colucci W S, Monrad E S, Smith, Harton S, Braunwald E 1986 J. Am. Coll. Cardiol. 7 661
Google Scholar
[31] Iyengar N, Peng C K, Morin R, Goldberger A L, Lipsitz L A 1996 Am. J. Physiol. 271 R1078
Google Scholar
[32] Goldberger A L, Peng C K, Lipsitz L A 2002 Neurobiol. Aging 23 23
Google Scholar
[33] Xiong W, Faes L, Ivanov P 2017 Phys. Rev. E 95 062114
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 413
- PDF Downloads: 11
- Cited By: 0
