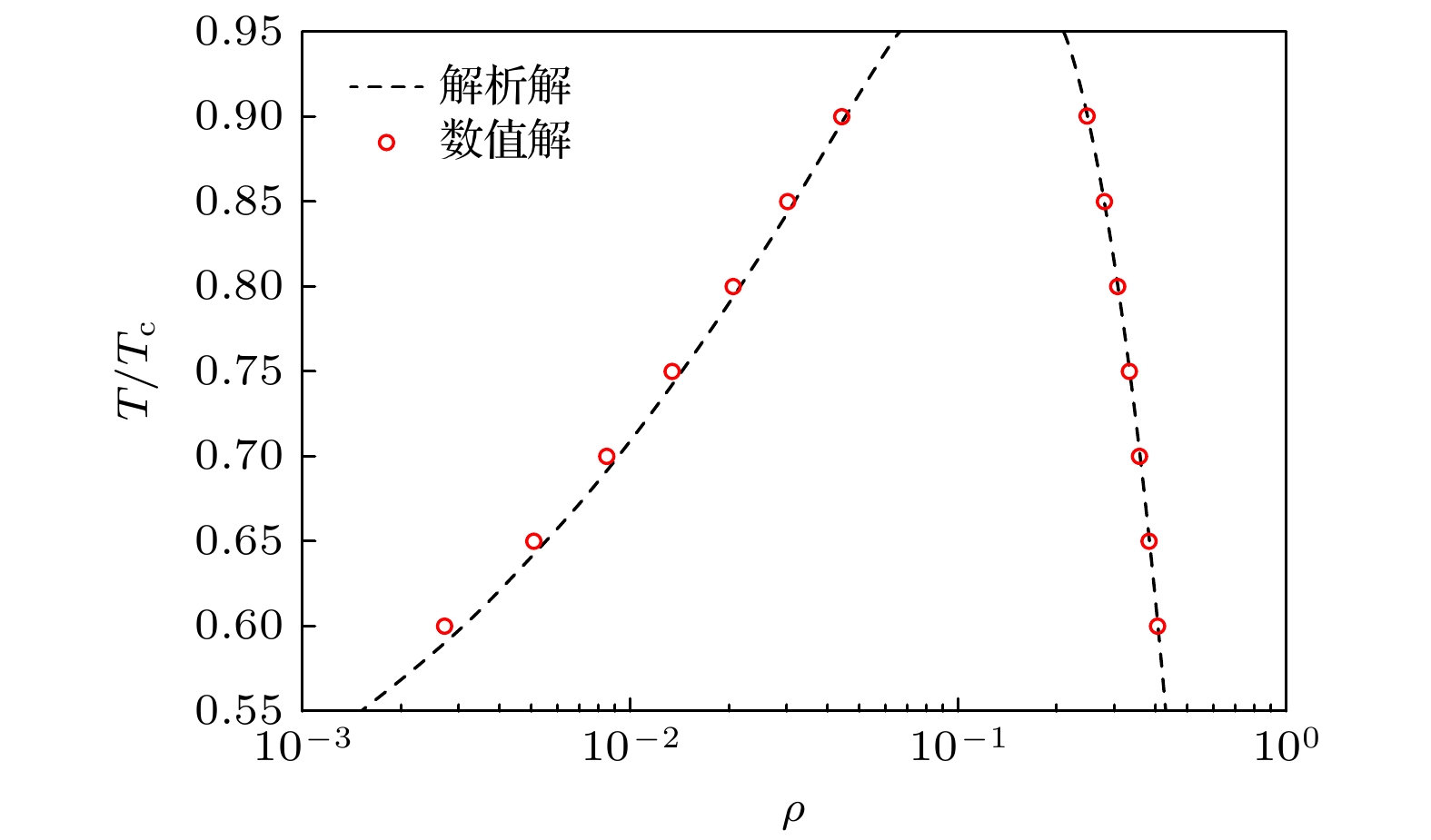
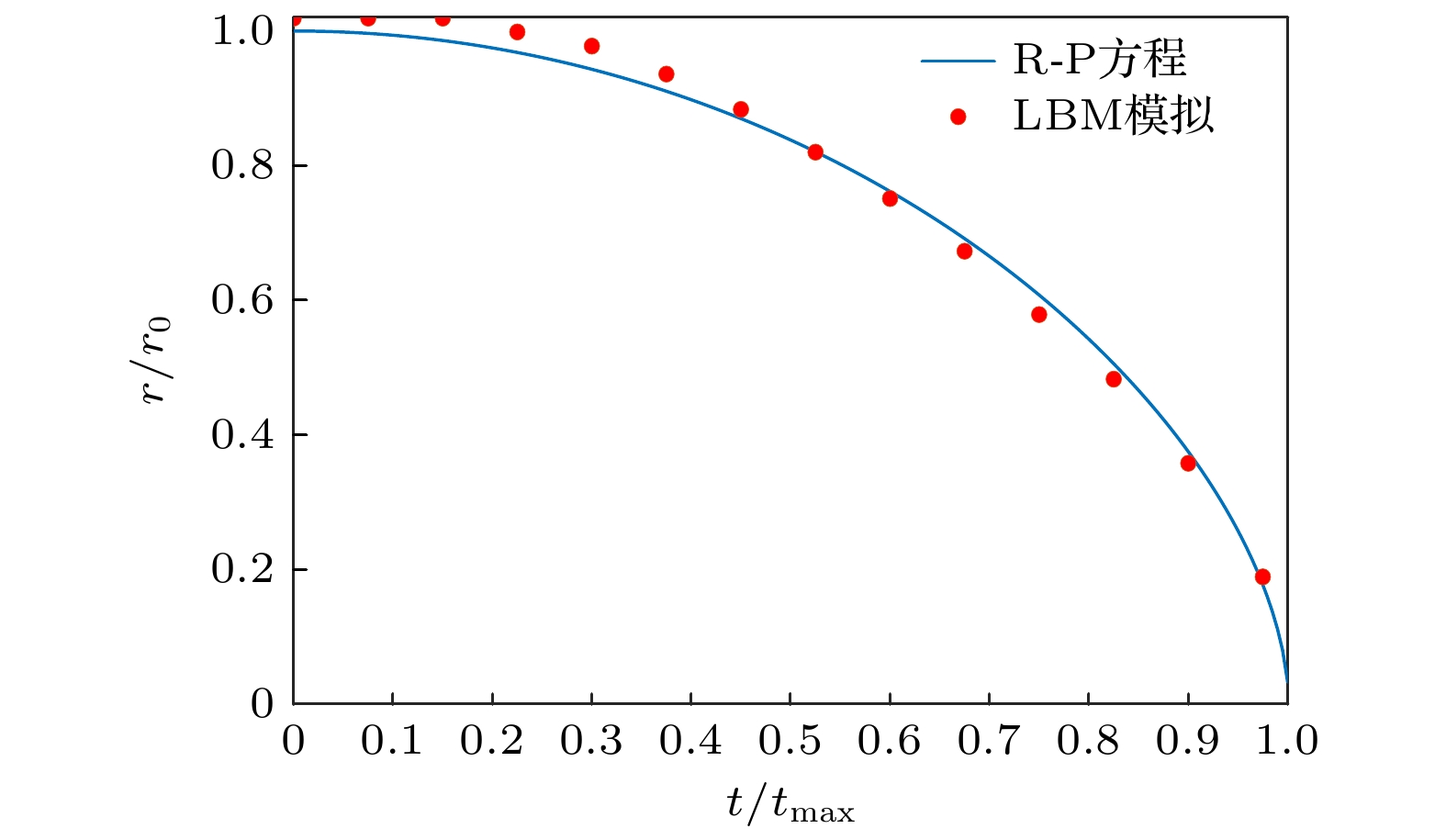
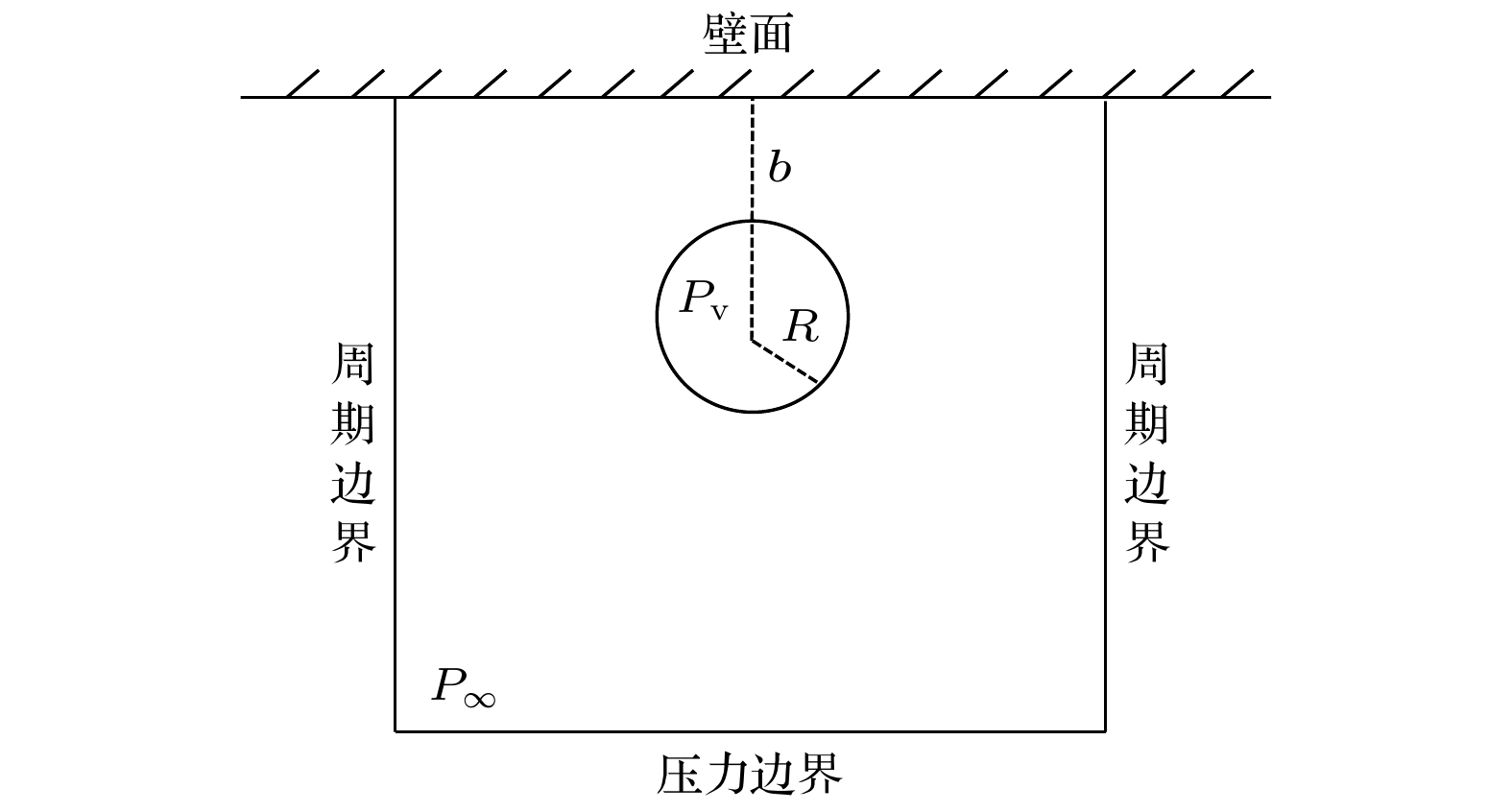
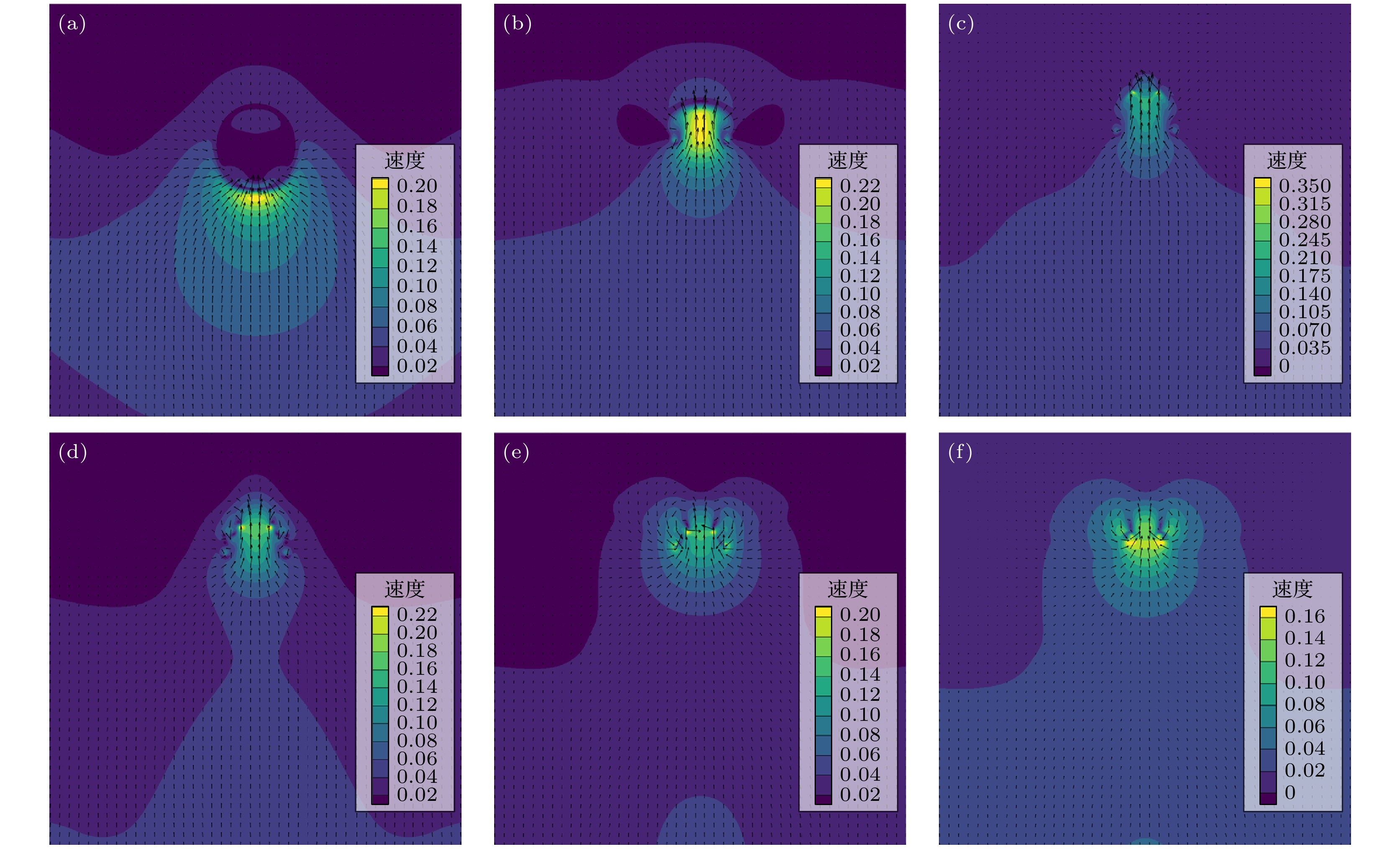
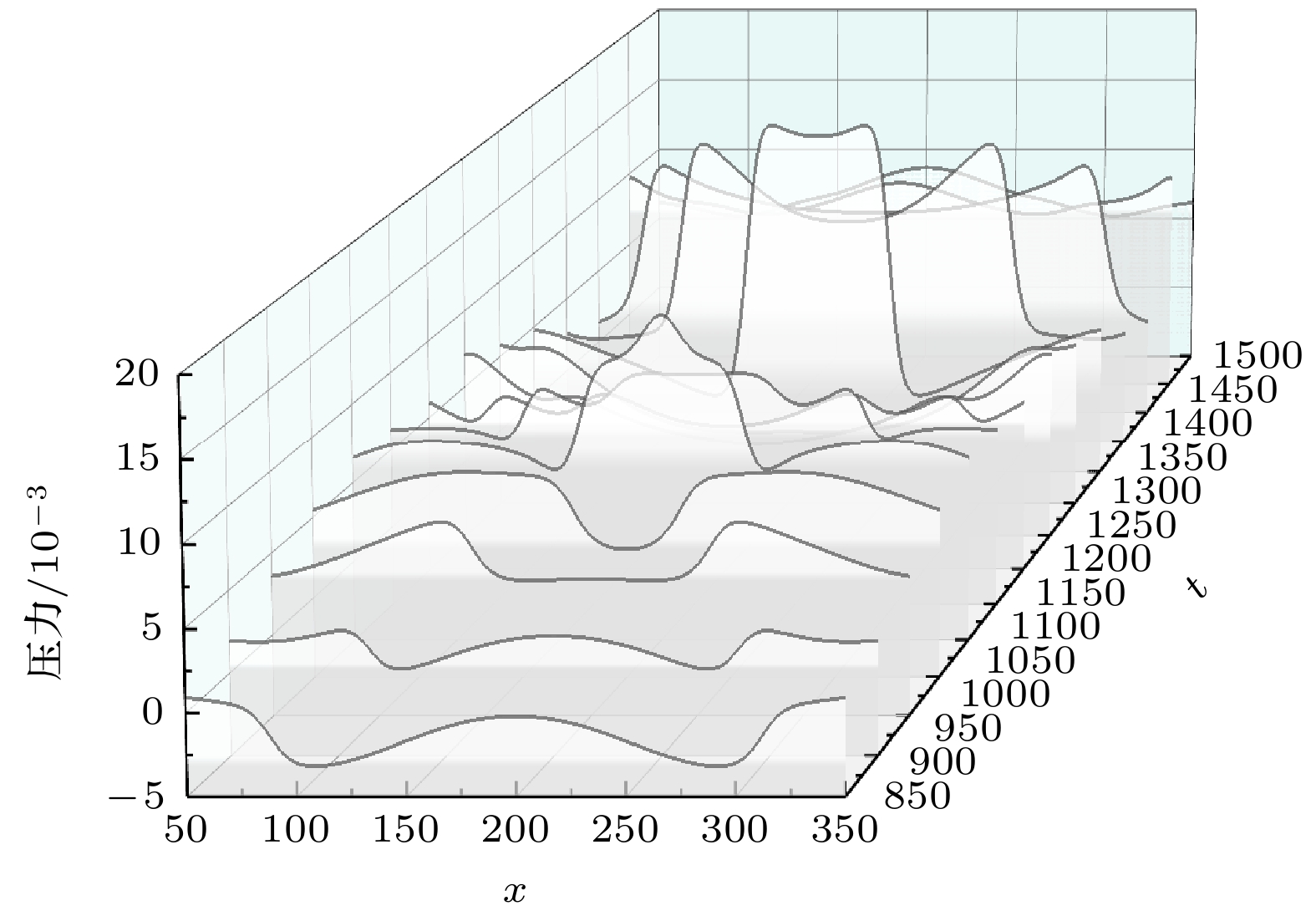
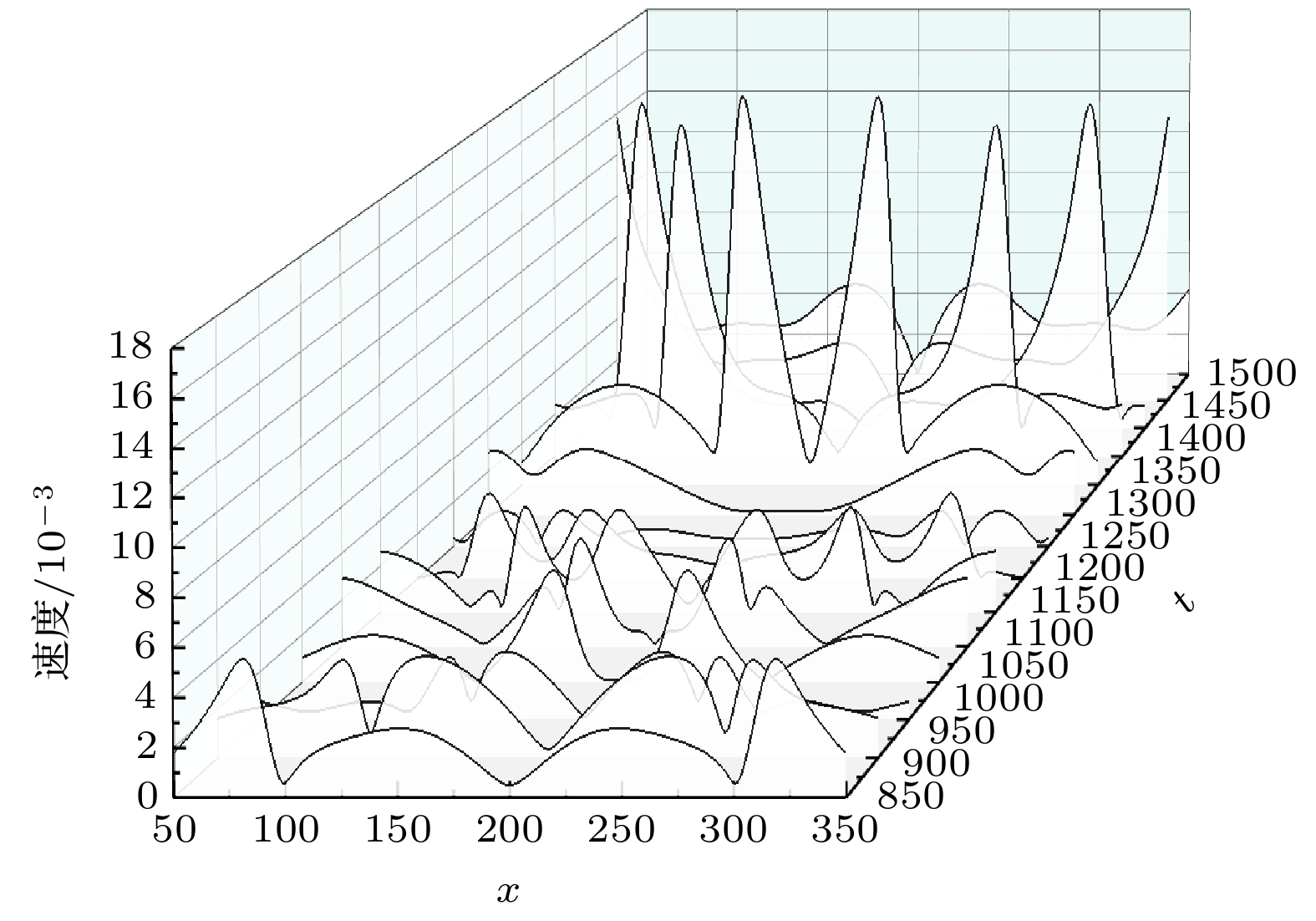
-
To reveal the load mechanism of wall damage induced by bubble collapse, the near-wall cavitation bubble collapse evolution is numerically simulated using an improved multi-relaxation-time lattice Boltzmann method (MRT-LBM), and the dynamic behavior of near-wall cavitation bubble is systematically analyzed. First, the improved multi-relaxation pseudopotential model with a modified force scheme is introduced and validated through the Laplace law and thermodynamic consistency. Subsequently, the near-wall bubble collapse evolution is simulated using the improved model, and the process of the bubble collapse evolution is obtained. The accuracy of the numerical simulation results is confirmed by comparing with previous experimental results. Based on the obtained flow field information, including velocity and pressure distributions, the dynamic behaviors during the bubble collapse are thoroughly analyzed. The results show that the micro-jets released during the near-wall bubble collapse primarily originate from the first collapse, while the shock waves are generated during both the first and the second collapse. Notably, the intensity of the shock waves produced during the second collapse is significantly higher than that during the first collapse. Furthermore, the distribution characteristics of pressure and velocity on the wall during the near-wall bubble collapse are analyzed, revealing the load mechanism of wall damage caused by bubble collapse. The results show that the wall is subjected to the combined effects of shock waves and micro-jets: shock waves cause large-area surface damage due to their extensive propagation range, whereas micro-jets lead to concentrated point damage with their localized high-velocity impact. In summary, this study elucidates the evolution of near-wall bubble collapse and the load mechanism of wall damage induced by bubble collapse, which provides theoretical support for further utilizing the cavitation effects and mitigation of cavitation-induced damage.
-
Keywords:
- multi-relaxation-time lattice Boltzmann method /
- pseudopotential model /
- collapse of near-wall bubble /
- cavitation erosion
[1] 任嘉乐 2023 硕士学位论文(兰州: 兰州理工大学)
Ren J L 2023 M. S. Thesis (Lanzhou: Lanzhou University of Technology
[2] 米建东 2022 硕士学位论文(兰州: 兰州理工大学)
Mi J D 2022 M. S. Thesis (Lanzhou: Lanzhou University of Technology
[3] Kling C L, Hammitt F G 1972 J. Basic Eng. 94 825
Google Scholar
[4] Plesset M S, Chapman R B 1971 J. Fluid Mech. 47 283
Google Scholar
[5] Li B B, Jia W, Zhang H C, Lu J 2014 Shock Waves 24 317
Google Scholar
[6] Aganin A A, Ilgamov M A, Kosolapova L A, Malakhov V G 2016 Thermophys. Aeromech. 23 211
Google Scholar
[7] 任晟, 张家忠, 张亚苗, 卫丁 2014 63 024702
Google Scholar
Ren S, Zhang J Z, Zhang Y M, Wei D 2014 Acta Phys. Sin. 63 024702
Google Scholar
[8] 李旭晖, 单肖文, 段文洋 2022 空气动力学学报 40 46
Google Scholar
Li X H, Shan X W, Duan W Y 2022 Acta Aerodyn. Sin. 40 46
Google Scholar
[9] Li X H, Shi Y Y, Shan X W 2019 Phys. Rev. E 100 013301
Google Scholar
[10] Shan X W, Chen H D 1993 Phys. Rev. E 47 1815
Google Scholar
[11] Shan X W, Chen H D 1994 Phys. Rev. E 49 2941
Google Scholar
[12] Sukop M C, Or D 2005 Phys. Rev. E 71 046703
Google Scholar
[13] Shan M L, Zhu C P, Zhou X, Yin C, Han Q B 2016 J. Hydrodyn. 28 442
Google Scholar
[14] Shan M L, Zhu Y, Yao C, Han Q B, Zhu C P 2017 J. Appl. Math. Phys. 5 1243
Google Scholar
[15] He X L, Zhang J M, Yang Q, Peng H N, Xu W L 2020 Phys. Rev. E 102 063306
Google Scholar
[16] Li Q, Luo K H, Li X J 2013 Phys. Rev. E 87 053301
Google Scholar
[17] Li Q, Luo K H, Li X J 2012 Phys. Rev. E 86 016709
Google Scholar
[18] Peng H N, Zhang J M, He X L, Wang Y R 2021 Comput. Fluids 217 104817
Google Scholar
[19] Liu Y, Peng Y 2021 J. Mar. Sci. Eng. 9 219
Google Scholar
[20] Yang Y, Shan M L, Kan X F, Shangguan Y Q, Han Q B 2020 Ultrason. Sonochem. 62 104873
Google Scholar
[21] Yang Y, Shan M L, Su N N, Kan X F, Shangguan Y Q, Han Q B 2022 Int. Commun. Heat Mass 134 105988
Google Scholar
[22] 何雅玲, 李庆, 王勇, 童自翔 2023 格子Boltzmann方法的理论及应用 (北京: 高等教育出版社) 第52页
He Y L, Li Q, Wang Y, Tong Z X 2023 Lattice Boltzmann Method: Theory and Applications (Beijing: Higher Education Press) p52
[23] 郭照立, 郑楚光 2009 格子Boltzmann方法的原理及应用 (北京: 科学出版社) 第46页
Guo Z L, Zheng C G 2009 Theory and Applications of Lattice Boltzmann Method (Beijing: Science Press) p46
[24] 任晟 2014 博士学位论文(西安: 西安交通大学)
Ren S 2014 Ph. D. Dissertation (Xi’an: Xi’an Jiaotong University
[25] Li Q, Luo K H, Kang Q J, Chen Q 2014 Phys. Rev. E 90 053301
Google Scholar
[26] Huang H, Sukop M C, Lu X 2015 Multiphase lattice Boltzmann methods: Theory and Application (New Jersey: Wiley Blackwell) p20
[27] Yuan P, Schaefer L 2006 Phys. Fluids 18 042101
Google Scholar
[28] 张新明, 周超英, Islam Shams, 刘家琦 2009 58 8406
Google Scholar
Zhang X M, Zhou C Y, Islam S, Liu J Q 2009 Acta Phys. Sin. 58 8406
Google Scholar
[29] Sofonea V, Biciuşcă T, Busuioc S, Ambruş V E, Gonnella G, Lamura A 2018 Phys. Rev. E 97 023309
Google Scholar
[30] Philipp A, Lauterborn W 1998 J. Fluid Mech. 361 75
Google Scholar
-
图 1 Laplace定律验证
Figure 1. Verification of Laplace’s law
图 2 共存密度数值解与解析解
Figure 2. Numerical and analytical solutions for coexistence density.
图 3 模拟结果与R-P方程对比
Figure 3. Simulation results and R-P equation results.
图 4 近壁空泡溃灭模型
Figure 4. Near-wall bubble collapse model.
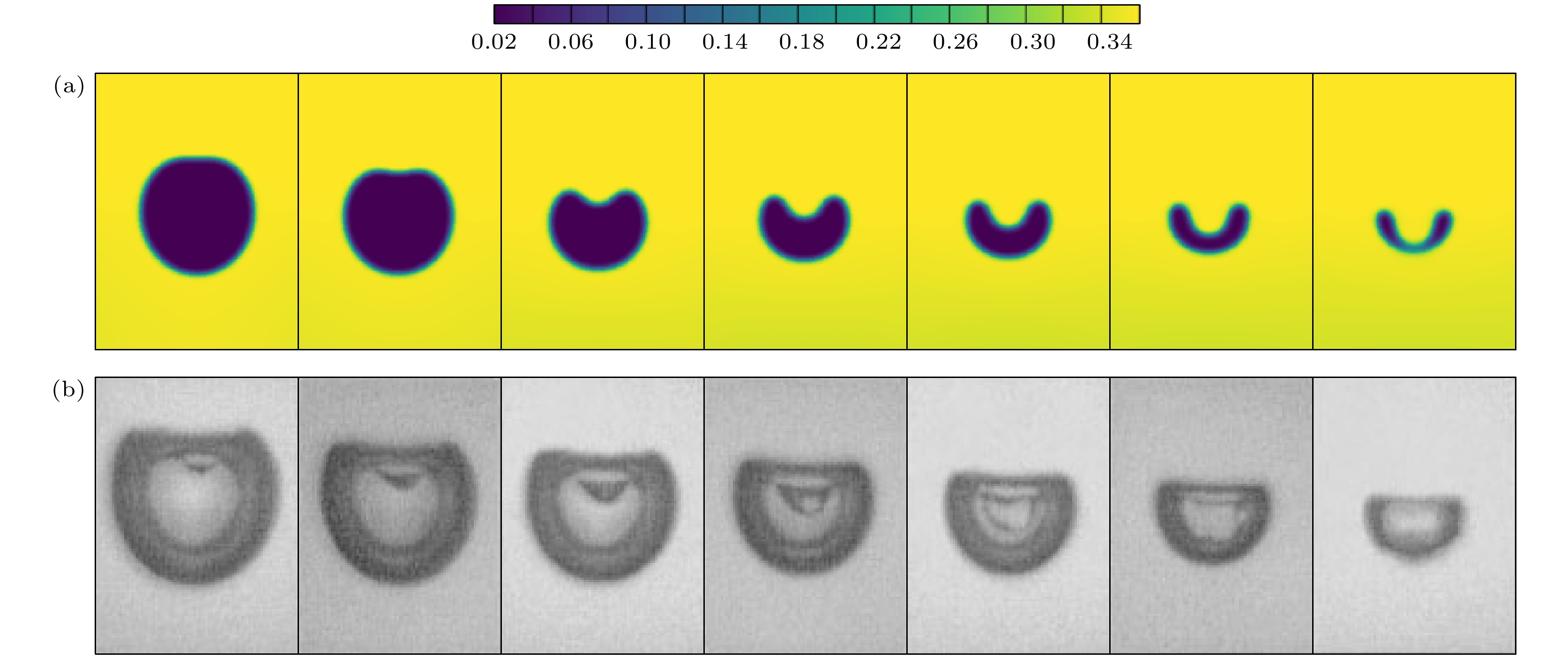
图 5 近壁空泡溃灭外形的演化数值模拟结果与实验结果对比 (a)数值模拟结果, $\lambda = 1.6, {\text{ }}{r_0} = 80$; (b)实验结果, $\lambda = 1.6,{r_0} = $$ 1.45 \times {10^{ - 3}}$ m
Figure 5. Comparison of numerical simulation results and experimental results on the evolution of near-wall bubble collapse shape: (a) Numerical simulation results, $\lambda = 1.6, {\text{ }}{r_0} = 80$; (b) experimental results, $\lambda = 1.6, {\text{ }}{r_0} = 1.45 \times {10^{ - 3}}$ m.
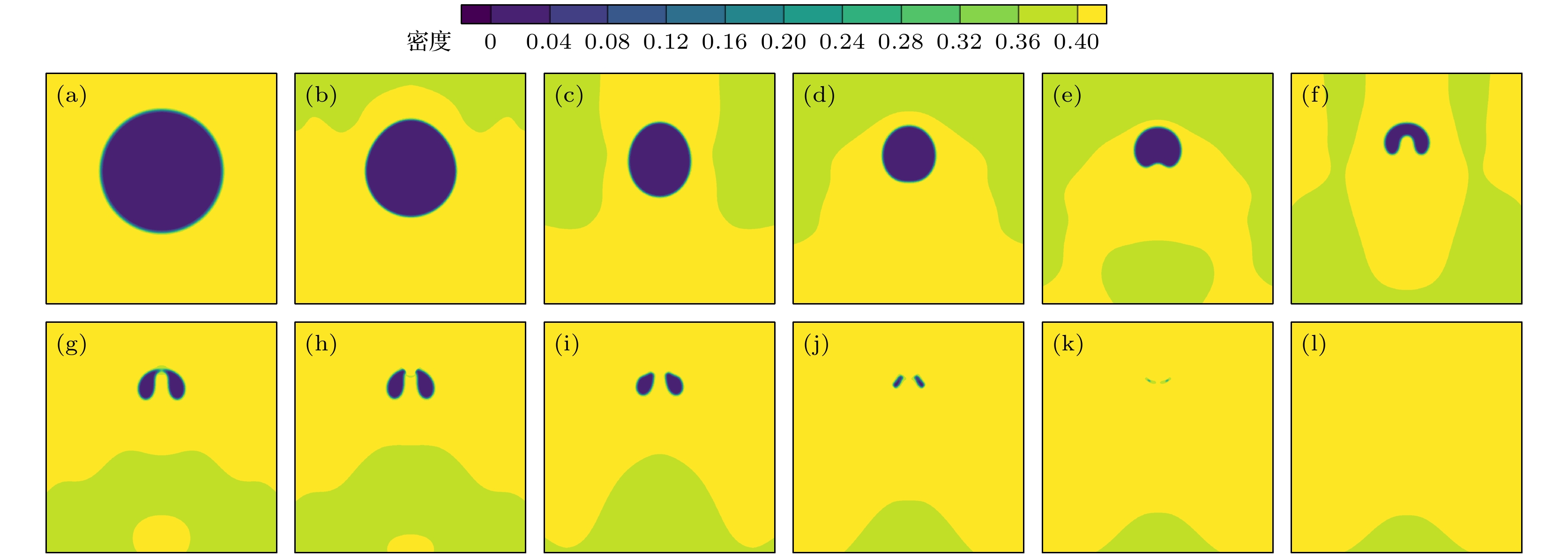
图 6 近壁空泡溃灭密度场演化过程 (a) t = 1 ts; (b) t = 300 ts; (c) t = 500 ts; (d) t = 600 ts; (e) t = 700 ts; (f) t = 850 ts; (g) t = 931 ts; (h) t = 950 ts; (i) t = 1050 ts; (j) t = 1150 ts; (k) t = 1175 ts; (l) t = 1180 ts
Figure 6. Density evolution of near-wall bubble: (a) t = 1 ts; (b) t = 300 ts; (c) t = 500 ts; (d) t = 600 ts; (e) t = 700 ts; (f) t = 850 ts; (g) t = 931 ts; (h) t = 950 ts; (i) t = 1050 ts; (j) t = 1150 ts; (k) t = 1175 ts; (l) t = 1180 ts.
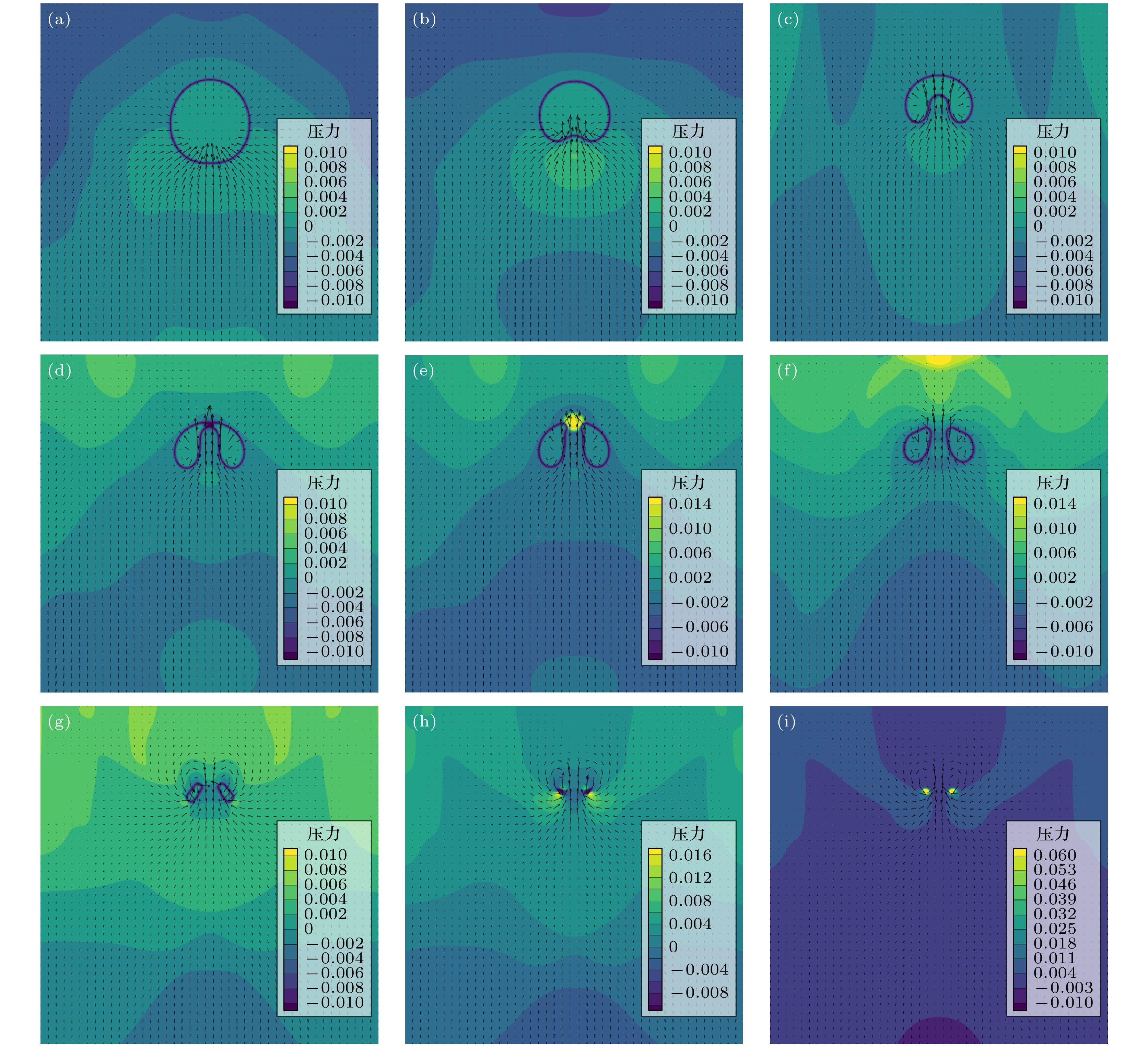
图 7 近壁空泡溃灭压力场演化过程 (a) t = 600 ts; (b) t = 700 ts; (c) t = 850 ts; (d) t = 931 ts; (e) t = 950 ts; (f) t = 1050 ts; (g) t = 1150 ts; (h) t = 1175 ts; (i) t = 1180 ts
Figure 7. Pressure evolution of near-wall bubble: (a) t = 600 ts; (b) t = 700 ts; (c) t = 850 ts; (d) t = 931 ts; (e) t = 950 ts; (f) t = 1050 ts; (g) t = 1150 ts; (h) t = 1175 ts; (i) t = 1180 ts.
图 8 近壁空泡溃灭速度场演化过程 (a) t = 600 ts; (b) t = 850 ts; (c) t = 950 ts; (d) t = 1050 ts; (e) t = 1150 ts; (f) t = 1180 ts
Figure 8. Velocity evolution of near-wall bubble: (a) t = 600 ts; (b) t = 850 ts; (c) t = 950 ts; (d) t = 1050 ts; (e) t = 1150 ts; (f) t = 1180 ts.
图 9 各时间步壁面处压力分布
Figure 9. Pressure distribution on the wall at each time step.
图 10 各时间步壁面处速度分布
Figure 10. Velocity distribution on the wall at each time step.
-
[1] 任嘉乐 2023 硕士学位论文(兰州: 兰州理工大学)
Ren J L 2023 M. S. Thesis (Lanzhou: Lanzhou University of Technology
[2] 米建东 2022 硕士学位论文(兰州: 兰州理工大学)
Mi J D 2022 M. S. Thesis (Lanzhou: Lanzhou University of Technology
[3] Kling C L, Hammitt F G 1972 J. Basic Eng. 94 825
Google Scholar
[4] Plesset M S, Chapman R B 1971 J. Fluid Mech. 47 283
Google Scholar
[5] Li B B, Jia W, Zhang H C, Lu J 2014 Shock Waves 24 317
Google Scholar
[6] Aganin A A, Ilgamov M A, Kosolapova L A, Malakhov V G 2016 Thermophys. Aeromech. 23 211
Google Scholar
[7] 任晟, 张家忠, 张亚苗, 卫丁 2014 63 024702
Google Scholar
Ren S, Zhang J Z, Zhang Y M, Wei D 2014 Acta Phys. Sin. 63 024702
Google Scholar
[8] 李旭晖, 单肖文, 段文洋 2022 空气动力学学报 40 46
Google Scholar
Li X H, Shan X W, Duan W Y 2022 Acta Aerodyn. Sin. 40 46
Google Scholar
[9] Li X H, Shi Y Y, Shan X W 2019 Phys. Rev. E 100 013301
Google Scholar
[10] Shan X W, Chen H D 1993 Phys. Rev. E 47 1815
Google Scholar
[11] Shan X W, Chen H D 1994 Phys. Rev. E 49 2941
Google Scholar
[12] Sukop M C, Or D 2005 Phys. Rev. E 71 046703
Google Scholar
[13] Shan M L, Zhu C P, Zhou X, Yin C, Han Q B 2016 J. Hydrodyn. 28 442
Google Scholar
[14] Shan M L, Zhu Y, Yao C, Han Q B, Zhu C P 2017 J. Appl. Math. Phys. 5 1243
Google Scholar
[15] He X L, Zhang J M, Yang Q, Peng H N, Xu W L 2020 Phys. Rev. E 102 063306
Google Scholar
[16] Li Q, Luo K H, Li X J 2013 Phys. Rev. E 87 053301
Google Scholar
[17] Li Q, Luo K H, Li X J 2012 Phys. Rev. E 86 016709
Google Scholar
[18] Peng H N, Zhang J M, He X L, Wang Y R 2021 Comput. Fluids 217 104817
Google Scholar
[19] Liu Y, Peng Y 2021 J. Mar. Sci. Eng. 9 219
Google Scholar
[20] Yang Y, Shan M L, Kan X F, Shangguan Y Q, Han Q B 2020 Ultrason. Sonochem. 62 104873
Google Scholar
[21] Yang Y, Shan M L, Su N N, Kan X F, Shangguan Y Q, Han Q B 2022 Int. Commun. Heat Mass 134 105988
Google Scholar
[22] 何雅玲, 李庆, 王勇, 童自翔 2023 格子Boltzmann方法的理论及应用 (北京: 高等教育出版社) 第52页
He Y L, Li Q, Wang Y, Tong Z X 2023 Lattice Boltzmann Method: Theory and Applications (Beijing: Higher Education Press) p52
[23] 郭照立, 郑楚光 2009 格子Boltzmann方法的原理及应用 (北京: 科学出版社) 第46页
Guo Z L, Zheng C G 2009 Theory and Applications of Lattice Boltzmann Method (Beijing: Science Press) p46
[24] 任晟 2014 博士学位论文(西安: 西安交通大学)
Ren S 2014 Ph. D. Dissertation (Xi’an: Xi’an Jiaotong University
[25] Li Q, Luo K H, Kang Q J, Chen Q 2014 Phys. Rev. E 90 053301
Google Scholar
[26] Huang H, Sukop M C, Lu X 2015 Multiphase lattice Boltzmann methods: Theory and Application (New Jersey: Wiley Blackwell) p20
[27] Yuan P, Schaefer L 2006 Phys. Fluids 18 042101
Google Scholar
[28] 张新明, 周超英, Islam Shams, 刘家琦 2009 58 8406
Google Scholar
Zhang X M, Zhou C Y, Islam S, Liu J Q 2009 Acta Phys. Sin. 58 8406
Google Scholar
[29] Sofonea V, Biciuşcă T, Busuioc S, Ambruş V E, Gonnella G, Lamura A 2018 Phys. Rev. E 97 023309
Google Scholar
[30] Philipp A, Lauterborn W 1998 J. Fluid Mech. 361 75
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 1377
- PDF Downloads: 52
- Cited By: 0
