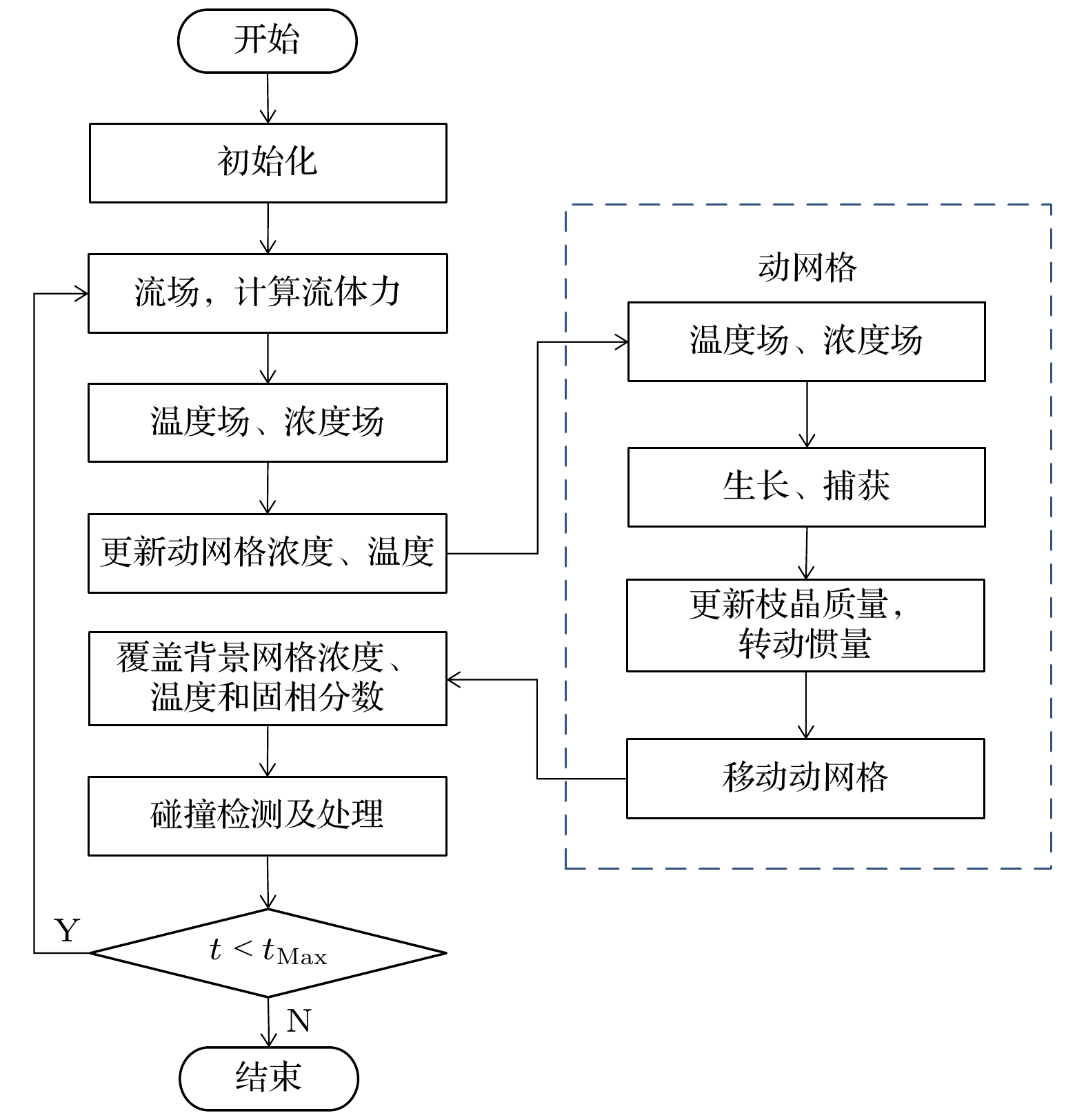
-
合金凝固过程中, 游离枝晶在熔体中的运动行为是研究合金凝固组织形成过程的关键问题之一. 元胞自动机-格子玻尔兹曼耦合模型是近年来进行凝固微观组织数值模拟的主要数值模型. 本文改进了模拟枝晶生长的元胞自动机和格子玻尔兹曼模型, 使其能够模拟过冷熔体中等轴晶的运动行为. 改进的模型采用伽利略不变的动量交换法计算流体力, 通过求解质心运动方程计算枝晶的运动位移, 并通过动网格技术实现枝晶的运动, 运用硬球模型处理枝晶的碰撞. 采用该模型模拟了Al-4.7%Cu合金过冷熔体中单枝晶的沉降、牛顿流体中两圆形粒子的沉降和两枝晶的弹性碰撞. 模拟结果表明, 本模型在计算枝晶生长运动过程时可以很好地维持枝晶的形貌. 采用本模型计算等轴枝晶的碰撞过程表明, 枝晶的运动会扰动其周围的熔体, 造成周围熔体浓度显著变化, 进而影响枝晶的生长, 加剧枝晶生长的不对称性.In the alloy solidification process, the movement behavior of free dendrites in the melt is one of the key issues in studying the formation process of the alloy solidification structure. The cellular automata-lattice Boltzmann coupling model has become a main numerical model for numerical simulation of solidification microstructure in recent years. In this paper, cellular automata and lattice Boltzmann model for simulating dendrite growth are improved to simulate the movement of equiaxed grains in undercooled melt. In the improved model, the Galilean invariant momentum exchange method is used to calculate the fluid force, the motion equation of the center of mass is solved to calculate the motion displacement of the dendrite, the motion of the dendrite is realized through the dynamic mesh technology, and the rigid sphere model is used to deal with the collision of the dendrite. The settlement of a single dendrite in the undercooled melt of Al-4.7% Cu alloy, the settlement of two round particles in the Newtonian fluid, and the elastic collision of two dendrites are all simulated by this model. The simulation results show that this model can maintain the morphology of dendrites well in the process of calculating dendrite growth motion, and this model can calculate the collision process of irregular dendrites. The movement of dendrite disturbs the melt around it, resulting in a significant change in the concentration of melt around it, which affects the growth of dendrite and aggravates the asymmetry of dendrite growth.
-
Keywords:
- cellular automata /
- lattice Boltzmann /
- dendrite collision /
- dynamic grid
[1] Wang Y B, Peng L M, Ji Y Z, Chen X X, Wang C L, Wu Y J, Fu Y N, Chen L Q 2018 J. Mater. Sci. Technol. 34 1142
[2] Lesoult G 2005 Mater. Sci. Eng., A 413 19
[3] Zhu M F, Dai T, Lee S Y, Hong C P 2008 Comput. Math. Appl. 55 1620
Google Scholar
[4] Sun D K, Zhu M F, Pan S Y, Raabe D 2009 Acta Mater. 57 1755
Google Scholar
[5] 潘诗琰, 朱鸣芳 2012 61 228102
Google Scholar
Pan S Y, Zhu M F 2012 Acta Phys. Sin. 61 228102
Google Scholar
[6] 潘诗琰, 朱鸣芳 2009 58 278
Google Scholar
Pan S Y, Zhu M F 2009 Acta Phys. Sin. 58 278
Google Scholar
[7] Chen R, Xu Q Y, Liu B C 2015 Comput. Mater. Sci. 105 90
Google Scholar
[8] Liu S Y, Hong K M, Shin Y C 2021 Comput. Mater. Sci. 192 110405
Google Scholar
[9] Qi X B, Chen Y, Kang X H, Li D Z, Gong T Z 2017 Sci. Rep. 7 45770
Google Scholar
[10] Meng S X, Zhang A, Guo Z P, Wang Q G 2020 Comput. Mater. Sci. 184 109784
Google Scholar
[11] Takaki T, Sato R, Rojas R, Ohno M, Shibuta Y 2018 Comput. Mater. Sci. 147 124
Google Scholar
[12] Ratkai L, Pusztai T, Granasy L 2019 npj Comput. Mater. 5 113
Google Scholar
[13] Sakane S, Takaki T, Ohno M, Shibuta Y, Aoki T 2020 Comput. Mater. Sci. 178 109639
Google Scholar
[14] 吴伟, 孙东科, 戴挺, 朱鸣芳 2012 61 150501
Google Scholar
Wu W, Sun D K, Dai T, Zhu M F 2012 Acta Phys. Sin. 61 150501
Google Scholar
[15] Fang H, Tang Q Y, Zhang Q Y, Gu T F, Zhu M F 2019 Int. J. Heat Mass Transfer 133 371
Google Scholar
[16] Lee W, Jeong Y, Lee J W, Lee H, Kang S H, Kim Y M, Yoon J 2020 J. Mater. Sci. Technol. 49 15
Google Scholar
[17] Cu C, Ridgeway C D, Moodispaw M P, Luo A A 2020 J. Mater. Process. Technol. 286 116829
Google Scholar
[18] Liu L, Pian S, Zhang Z, Bao Y, Li R, Chen H 2018 Comput. Mater. Sci. 146 9
Google Scholar
[19] Wu J Y, Sun D K, Wang J C, Zhu M F 2020 Eur. Phys. J. E 43 30
Google Scholar
[20] Zhang Q Y, Sun D K, Pan S Y, Zhu M F 2020 Int. J. Heat Mass Transfer 146 118838
Google Scholar
[21] Sun D K, Zhu M F, Pan S Y, Yang C R, Raabe D 2011 Comput. Math. Appl. 61 3585
Google Scholar
[22] Rappaz M, Thévoz P H 1987 Acta Metall. 35 2929
Google Scholar
[23] Zhu M F, Stefanescu D 2007 Acta Mater. 55 1741
Google Scholar
[24] Wen B H, Zhang C Y, Tu Y S, Wang C L, Fang H P 2014 J. Comput. Phys. 266 161
Google Scholar
[25] Mei R, Yu D, Shyy W, Luo L S 2002 Phys. Rev. E: Stat. Nonliner Soft Matter Phys. 65 041203
Google Scholar
[26] Wu M, Ludwig A, Fjeld A 2010 Comput. Mater. Sci. 50 43
Google Scholar
[27] Feng Z G, Michaelides E E 2004 J. Comput. Phys. 195 602
Google Scholar
-
图 3 自然对流下单枝晶沉降过程中溶质浓度和流体速度的时间演化 (a) t = 0.005 s; (b) t = 0.015 s; (c) t = 0.025 s
Fig. 3. Evolution of solute concentration and fluid velocity during precipitation of single dendrite under natural convection: (a) t = 0.005 s; (b) t = 0.015 s; (c) t = 0.025 s.
图 4 t = 0.015 s时, 模拟域O点处竖直方向上的溶质浓度变化
Fig. 4. When t = 0.015 s, the solute concentration change in the vertical direction at point O in the simulation domain.
图 6 两个球形粒子沉降过程中, 四个时间的瞬时涡量轮廓 (a) 1 .0 s; (b) 1.5 s; (c) 2.5 s; (d) 4.0 s
Fig. 6. The instantaneous vorticity profiles of two spherical particles in the process of settling at four times: (a) 1.0 s; (b) 1.5 s; (c) 2.5 s; (d) 4.0 s.
图 7 粒子质心坐标 (a) 横坐标; (b) 纵坐标
Fig. 7. Coordinates of the particles centroid: (a) Transverse coordinates; (b) longitudinal coordinates.
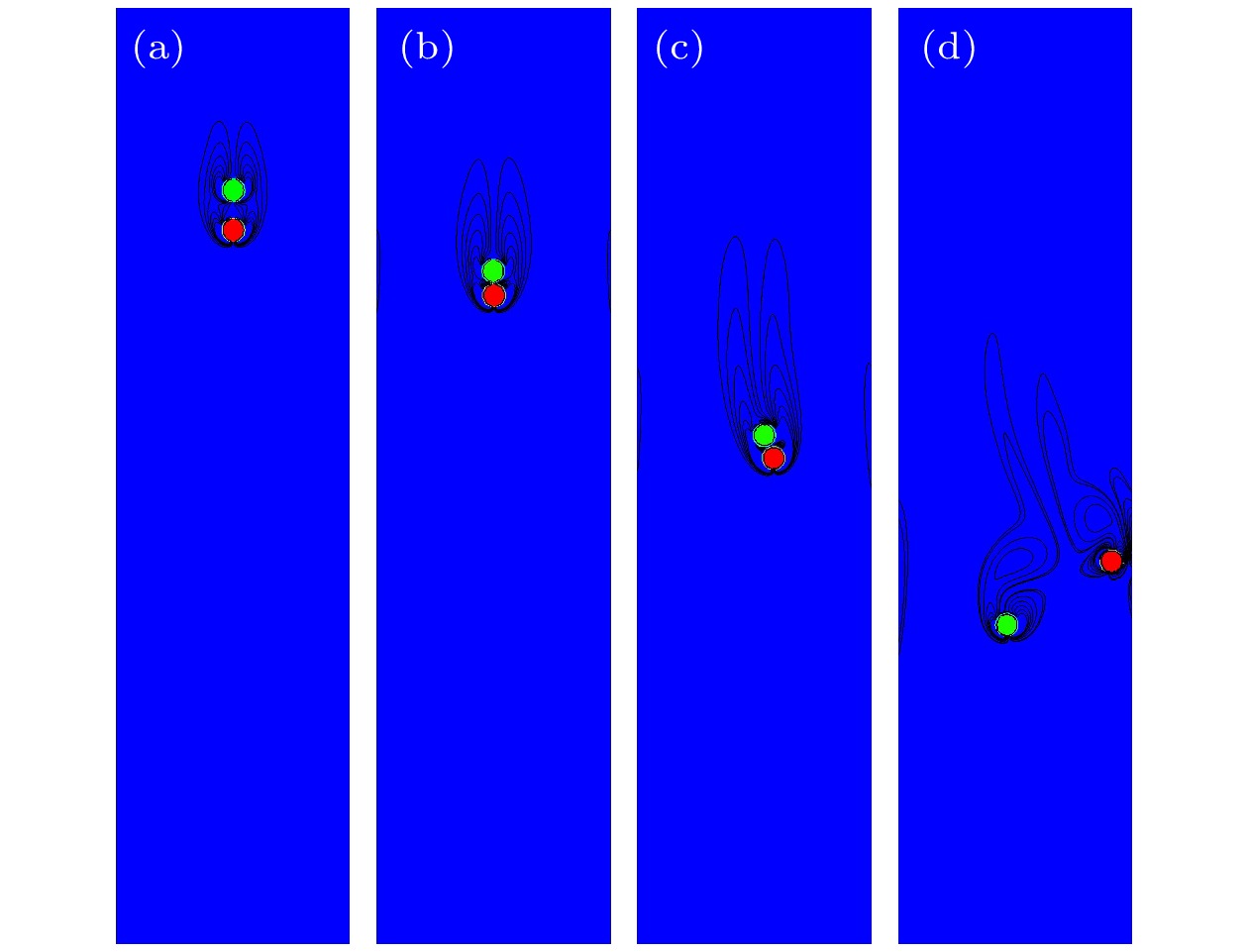
图 8 枝晶偏心碰撞形貌图 (a) 0.008 s; (b) 0.0089 s; (c) 0.009 s; (d) 0.00915 s. 箭头表示速度v的大小和方向, 灰度表示流体溶质浓度C
Fig. 8. The morphology of dendrite eccentric collision: (a) 0.008 s; (b) 0.0089 s; (c) 0.009 s; (d) 0.00915 s . The arrow indicates the size and direction of velocity v, and the gray scale indicates the concentration of solute C.
表 1 Al-4.7%Cu(质量含量)合金的热物性参数[26]
Table 1. Physical properties of Al-4.7%Cu (weight percent) alloy[26].
Physical parameter Value Melting temperature, Tm/K 933.3 Solidification temperature, T0/K 920.1 Diffusivity in liquid, D/(10–9 m2·s–1) 3.0 Partition coefficient, k 0.145 Gibbs-Tomson coefficient, Γ/(10–7 m·K) 2.4 Specific heat capacity, Cp/(J·kg–1·K–1) 1179 Latent heat, L/(103 J·kg–1) 397 Density, ρ/(kg·m–3) 2606 
下载: 导出CSV
-
[1] Wang Y B, Peng L M, Ji Y Z, Chen X X, Wang C L, Wu Y J, Fu Y N, Chen L Q 2018 J. Mater. Sci. Technol. 34 1142
[2] Lesoult G 2005 Mater. Sci. Eng., A 413 19
[3] Zhu M F, Dai T, Lee S Y, Hong C P 2008 Comput. Math. Appl. 55 1620
Google Scholar
[4] Sun D K, Zhu M F, Pan S Y, Raabe D 2009 Acta Mater. 57 1755
Google Scholar
[5] 潘诗琰, 朱鸣芳 2012 61 228102
Google Scholar
Pan S Y, Zhu M F 2012 Acta Phys. Sin. 61 228102
Google Scholar
[6] 潘诗琰, 朱鸣芳 2009 58 278
Google Scholar
Pan S Y, Zhu M F 2009 Acta Phys. Sin. 58 278
Google Scholar
[7] Chen R, Xu Q Y, Liu B C 2015 Comput. Mater. Sci. 105 90
Google Scholar
[8] Liu S Y, Hong K M, Shin Y C 2021 Comput. Mater. Sci. 192 110405
Google Scholar
[9] Qi X B, Chen Y, Kang X H, Li D Z, Gong T Z 2017 Sci. Rep. 7 45770
Google Scholar
[10] Meng S X, Zhang A, Guo Z P, Wang Q G 2020 Comput. Mater. Sci. 184 109784
Google Scholar
[11] Takaki T, Sato R, Rojas R, Ohno M, Shibuta Y 2018 Comput. Mater. Sci. 147 124
Google Scholar
[12] Ratkai L, Pusztai T, Granasy L 2019 npj Comput. Mater. 5 113
Google Scholar
[13] Sakane S, Takaki T, Ohno M, Shibuta Y, Aoki T 2020 Comput. Mater. Sci. 178 109639
Google Scholar
[14] 吴伟, 孙东科, 戴挺, 朱鸣芳 2012 61 150501
Google Scholar
Wu W, Sun D K, Dai T, Zhu M F 2012 Acta Phys. Sin. 61 150501
Google Scholar
[15] Fang H, Tang Q Y, Zhang Q Y, Gu T F, Zhu M F 2019 Int. J. Heat Mass Transfer 133 371
Google Scholar
[16] Lee W, Jeong Y, Lee J W, Lee H, Kang S H, Kim Y M, Yoon J 2020 J. Mater. Sci. Technol. 49 15
Google Scholar
[17] Cu C, Ridgeway C D, Moodispaw M P, Luo A A 2020 J. Mater. Process. Technol. 286 116829
Google Scholar
[18] Liu L, Pian S, Zhang Z, Bao Y, Li R, Chen H 2018 Comput. Mater. Sci. 146 9
Google Scholar
[19] Wu J Y, Sun D K, Wang J C, Zhu M F 2020 Eur. Phys. J. E 43 30
Google Scholar
[20] Zhang Q Y, Sun D K, Pan S Y, Zhu M F 2020 Int. J. Heat Mass Transfer 146 118838
Google Scholar
[21] Sun D K, Zhu M F, Pan S Y, Yang C R, Raabe D 2011 Comput. Math. Appl. 61 3585
Google Scholar
[22] Rappaz M, Thévoz P H 1987 Acta Metall. 35 2929
Google Scholar
[23] Zhu M F, Stefanescu D 2007 Acta Mater. 55 1741
Google Scholar
[24] Wen B H, Zhang C Y, Tu Y S, Wang C L, Fang H P 2014 J. Comput. Phys. 266 161
Google Scholar
[25] Mei R, Yu D, Shyy W, Luo L S 2002 Phys. Rev. E: Stat. Nonliner Soft Matter Phys. 65 041203
Google Scholar
[26] Wu M, Ludwig A, Fjeld A 2010 Comput. Mater. Sci. 50 43
Google Scholar
[27] Feng Z G, Michaelides E E 2004 J. Comput. Phys. 195 602
Google Scholar
下载:
计量
- 文章访问数: 4558
- PDF下载量: 66
- 被引次数: 0
