-
It has been found experimentally that learning during wakefulness leads to a net enhancement of synaptic strength, accompanied by the neural dynamical transition from tonic to bursting firing, while the net synaptic strength decreases to a baseline level during sleep, accompanied by the transition from bursting to tonic firing. In this paper, we establish a model of synaptic plasticity, which can realize synaptic strength changes and neural dynamical transitions in wakefulness-sleep cycle by using the coupled Hindmarsh-Rose neurons. Through numerical simulation and theoretical analysis, it is further found that the average synaptic weight of the neural network can reach a stable value during either prolonged wakefulness or prolonged sleep, which depends on the ratio of some specific parameters in the model. Particularly, the synaptic weight exhibits a stable log-normal distribution observed in a real neural system, when the average synaptic weight reaches a stable value. Moreover, the fluctuation of this weight distribution is positively correlated with the fluctuation of noise in the synaptic plasticity model. The provided model of the synaptic plasticity and its dynamics results can provide a theoretical reference for studying the physiological mechanism of synaptic plasticity and neuronal firings during the wakefulness-sleep cycle, and they are expected to have potential applications in the development of therapeutic interventions for sleep disorders.
-
Keywords:
- neural networks /
- synaptic plasticity /
- neural dynamics /
- synchronization
[1] Siegel J M 2001 Science 294 1058
Google Scholar
[2] Diekelmann S, Born J 2010 Nat. Rev. Neurosci. 11 114
Google Scholar
[3] Inostroza M, Born J 2013 Annu. Rev. Neurosci. 36 79
Google Scholar
[4] De Lavilléon G, Lacroix M M, Rondi-Reig L, Benchenane K 2015 Nat. Neurosci. 18 493
Google Scholar
[5] Tononi G, Cirelli C 2006 Sleep Med. Rev. 10 49
Google Scholar
[6] Stickgold R, Hobson J A, Fosse R, Fosse M 2001 Science 294 1052
Google Scholar
[7] Tononi G, Cirelli C 2003 Brain Res. Bull. 62 143
Google Scholar
[8] McCormick D A, Feeser H R 1990 Neurosci. 39 103
Google Scholar
[9] Steriade M, Nuñez A, Amzica F 1993 J. Neurosci. 13 3252
Google Scholar
[10] Steriade M, McCormick D A, Sejnowski T J 1993 Science 262 679
Google Scholar
[11] Postnova S, Voigt K, Braun H A 2007 J. Biol. Phys. 33 129
Google Scholar
[12] Zhou J F, Jiang E H, Xu B L, Xu K, Zhou C, Yuan W J 2021 Phys. Rev. E 104 054407
Google Scholar
[13] Dhamala M, Jirsa V K, Ding M 2004 Phys. Rev. Lett. 92 028101
Google Scholar
[14] Nguyen T, Babawale O, Kim T, Jo H J, Liu H, Kim J G 2018 Sci. Rep. 8 16144
Google Scholar
[15] Curtis B J, Williams P G, Jones C R, Anderson J S 2016 Brain Behav. 6 e00576
Google Scholar
[16] Xu B L, Zhou J F, Li R, Jiang E H, Yuan W J 2023 Physica A 617 128663
Google Scholar
[17] Abbott L F, Regehr W G 2004 Nature 431 796
Google Scholar
[18] Destexhe A, Marder E 2004 Nature 431 789
Google Scholar
[19] Caporale N, Dan Y 2008 Annu. Rev. Neurosci. 31 25
Google Scholar
[20] Zhou J F, Yuan W J, Chen D, Wang B H, Zhou Z, Boccaletti S, Wang Z 2019 Phys. Rev. E 99 032419
Google Scholar
[21] Song S, Miller K D, Abbott L F 2000 Nat. Neurosci. 3 919
Google Scholar
[22] Yuan W J, Zhou J F, Zhou C 2013 PLoS One 8 e84644
Google Scholar
[23] Babadi B, Abbott L F 2010 PLoS Comput. Biol. 6 e1000961
Google Scholar
[24] 王美丽, 王峻松 2015 64 108701
Google Scholar
Wang M L, Wang J S 2015 Acta Phys. Sin. 64 108701
Google Scholar
[25] Takahashi Y K, Kori H, Masuda N 2009 Phys. Rev. E 79 051904
Google Scholar
[26] Meisel C, Gross T 2009 Phys. Rev. E 80 061917
Google Scholar
[27] Andrade K C, Spoormaker V I, Dresler M, Wehrle R, Holsboer F, Sämann P G, Czisch M 2011 J. Neurosci. 31 10331
Google Scholar
[28] Hindmarsh J L, Rose R M 1984 Proc. R. Soc. Lond. B Biol. Sci. 221 87
Google Scholar
[29] Erdős P, Rényi A 1960 Publ. Math. Inst. Hung. Acad. Sci. 5 17
[30] Vanvreeswijk C, Sompolinsky H 1996 Science 274 1724
Google Scholar
[31] Vogels T P, Abbott L F 2005 J. Neurosci. 25 10786
Google Scholar
[32] Bi G Q, Poo M 1998 J. Neurosci. 18 10464
Google Scholar
[33] Van Rossum M C W, Bi G Q, Turrigiano G G 2000 J. Neurosci. 20 8812
Google Scholar
[34] McCormick D A 1992 J. Clin. Neurophysiol. 9 212
Google Scholar
[35] Steriade M 2003 Front. Biosci. 8 878
Google Scholar
[36] Li K T, Liang J, Zhou C 2021 Neural Plast. 2021 6668175
Google Scholar
[37] Wang S, Zhou C 2009 Phys. Rev. E 79 061910
Google Scholar
[38] Vyazovskiy V V, Olcese U, Hanlon E C, Nir Y, Cirelli C, Tononi G 2011 Nature 472 443
Google Scholar
[39] Buzsáki G, Mizuseki K 2014 Nat. Rev. Neurosci. 15 264
Google Scholar
[40] Song S, Sjöström P J, Reigl M, Nelson S, Chklovskii D B 2005 PLoS Biol. 3 e68
Google Scholar
-
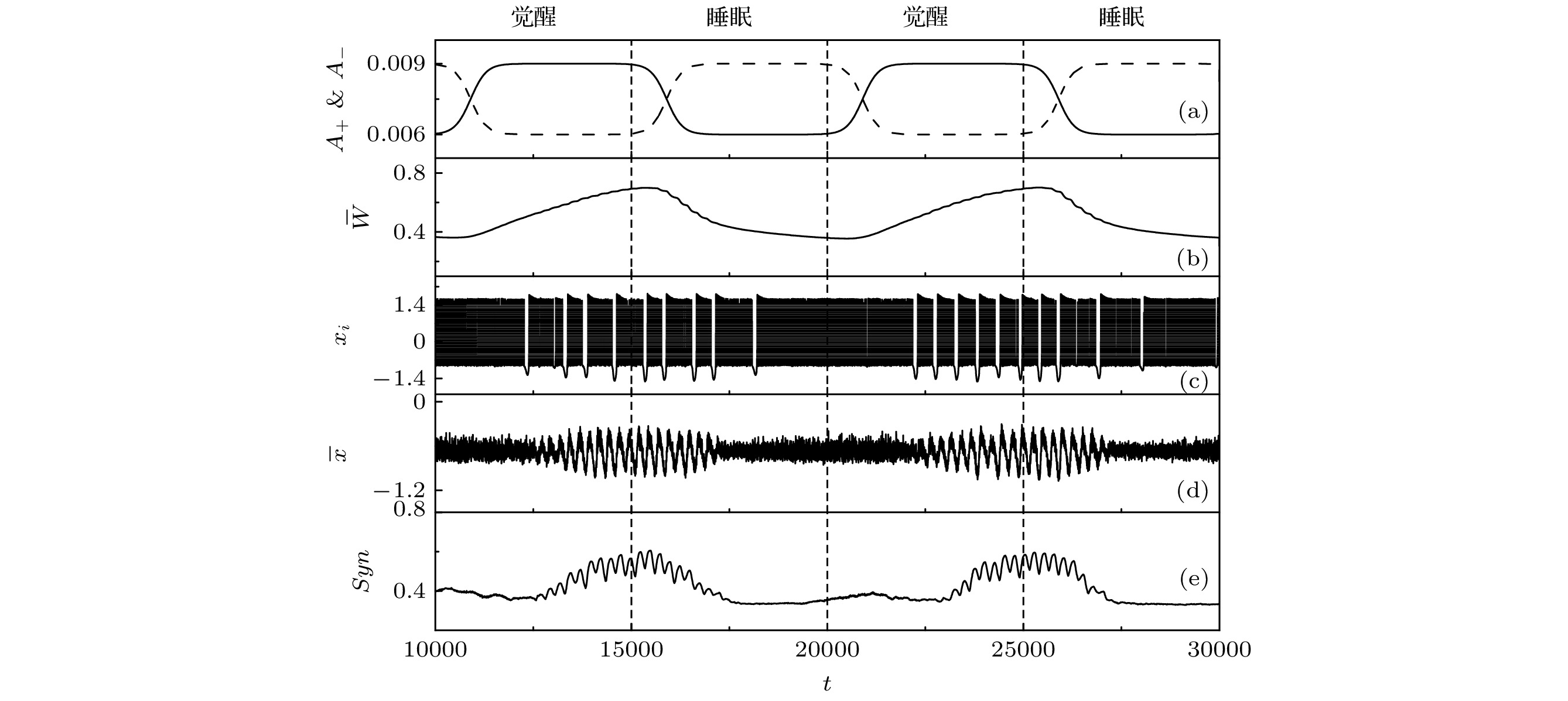
图 1 突触可塑性引起觉醒-睡眠周期中突触强度的变化和神经动力学的转变 (a) $A_{+}$(实线)和$A_{-}$(虚线)的变化, 觉醒: $A_{+} = 0.006 $$ +\;0.003 \dfrac{1}{1+{\text{e}}^{-0.005(t'-900)}}$, $A_{-}=0.006+0.003 \left[1-\dfrac{1}{1+{\text{e}}^{-0.005(t'-900)}}\right]$, 睡眠: $A_{-}=0.006+0.003 \dfrac{1}{1+{\text{e}}^{-0.005(t''-900)}}$, $A_{+} = 0.006+0.003 \left[1-\dfrac{1}{1+{\text{e}}^{-0.005(t''-900)}}\right]$, 其中$t'$表示t除以$10000$的余数, $t''$表示t除以$5000$的余数; (b)平均突触权值$\overline{W}$; (c)随机选定的神经元$i$的膜电位$x_i$; (d) 平均膜电位$\overline{x}$; (e)网络的同步指数$Syn$. 垂直虚线表示觉醒和睡眠之间的交替时刻. 参数$A_+$和$A_-$的取值为$0.009$和$0.006$, 并且它们的值在觉醒和睡眠交替时也迅速交替. 参数$\tau_+=\tau_-=25$, $c_{{{\mathrm{p}}}}=1$ 和$c_{{{\mathrm{d}}}}=2$
Figure 1. Synaptic changes and neural dynamical transitions induced by the synaptic plasticity for wakefulness-sleep cycle. (a) Changes of $A_{+}$ (solid line) and $A_{-}$ (dashed line). Wakefulness: $A_{+}=0.006+0.003\dfrac{1}{1+{{{\mathrm{e}}}}^{-0.005(t'-900)}}$, $A_{-}=0.006+ 0.003\Big[1- $$ \dfrac{1}{1+{{{\mathrm{e}}}}^{-0.005(t'-900)}}\Big]$, sleep: $A_{-}=0.006+0.003\dfrac{1}{1+{{{\mathrm{e}}}}^{-0.005(t''-900)}}$, $A_{+}=0.006+0.003\left[1-\dfrac{1}{1+{{{\mathrm{e}}}}^{-0.005(t''-900)}}\right]$, where$t'$ represents the remainder of t divided by $10000$ and $t''$ represents the remainder of t divided by $5000$. (b) Average synaptic weight $\overline{W}$. (c) Potential $x_i$ of a randomly chosen neuron $i$. (d) Average potential $\overline{x}= \dfrac1 N \displaystyle\sum\nolimits^N_{i=1}x_i$. (e) Synchrony index $Syn$ of the network. The vertical dashed lines indicate moments of exchange between wakefulness and sleep. Parameters $A_+$ and $A_-$ rapidly exchange between $0.009$ and $0.006$ in very short periods during wakefulness and sleep. Here, parameters $\tau_+=\tau_-=25$, $c_{{{\mathrm{p}}}}=1$ and $c_{{{\mathrm{d}}}}=2$ are given during both wakefulness and sleep.
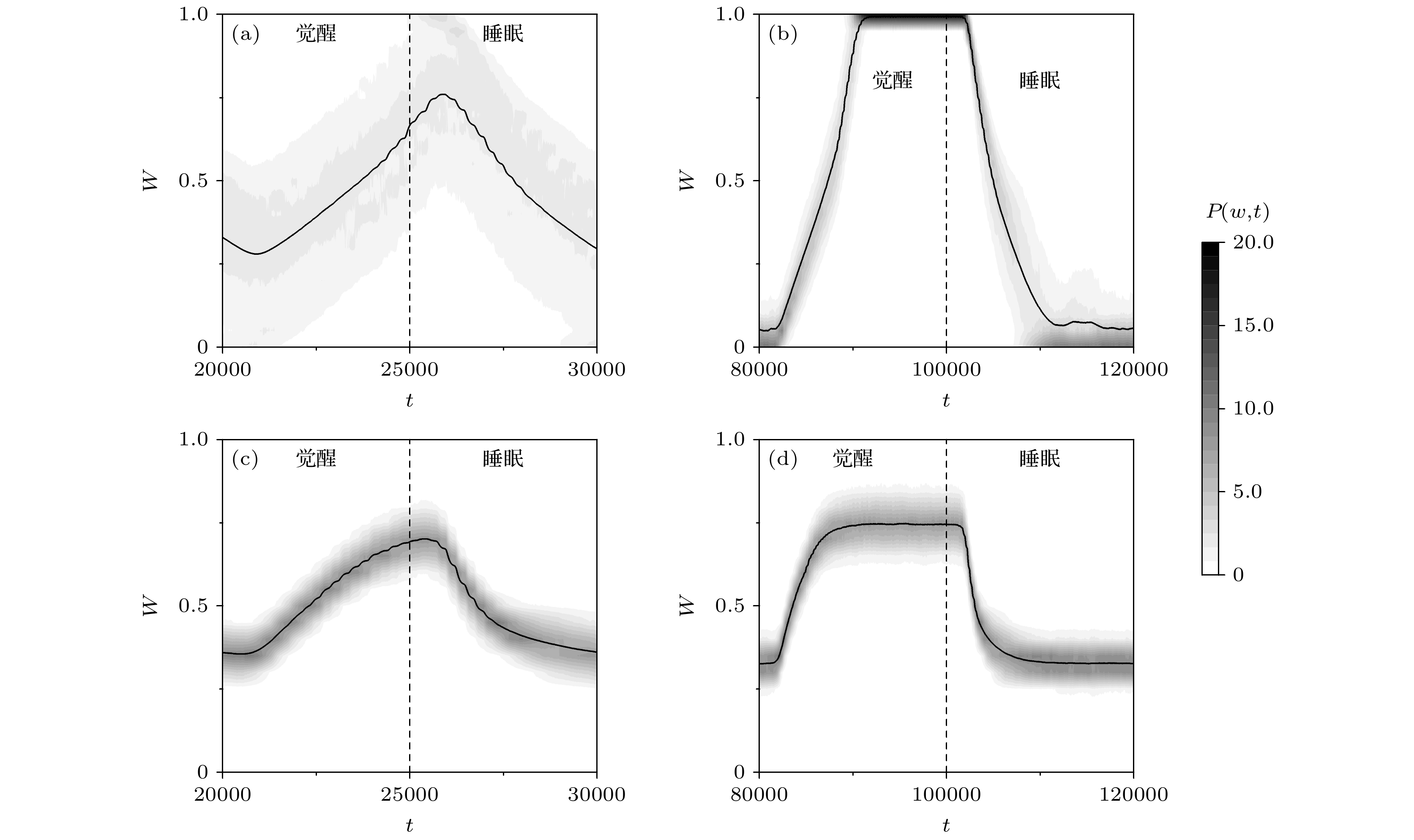
图 2 在一个觉醒-睡眠周期内, 突触权值分布概率密度$P(W, t)$的灰度图及网络平均突触权值$\overline{W}$的变化曲线(实线) (a), (b)不含有权值依赖的原始STDP情况; (c), (d)含有权值依赖的改进STDP情况; 觉醒睡眠周期设置为10000 (a), (c) 和40000 (b), (d); 垂直虚线表示觉醒和睡眠的交替时刻
Figure 2. Gray-scale plots of probability density $P(W, t)$ for weight distribution and the average synaptic weight $\overline{W}$ (solid line) in the absence of weight dependence (a), (b) and in the presence of weight dependence (c), (d), for the different periods of wakefulness-sleep cycle, 10000 (a), (c) and 40000 (b), (d). The vertical dashed lines indicate the moments of exchange between wakefulness and sleep.
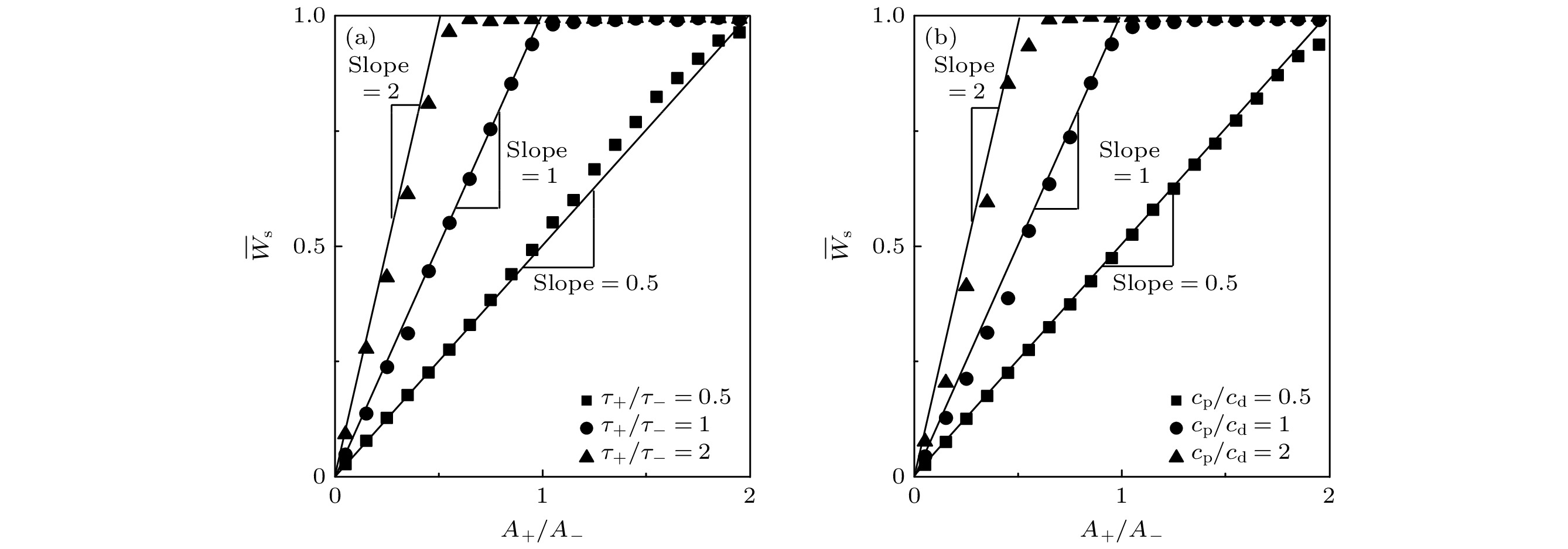
图 3 稳定的平均突触权值$\overline{W}_{\text{s}}$与比值$A_+/A_-$的函数关系 (a) $c_{\text{p}}=c_{\text{d}}=1$固定不变, $\tau_+/\tau_-$取不同的比值; (b) $\tau_+=\tau_-= $$ 25$固定不变, $c_{\text{p}}/c_{\text{d}}$取不同的比值. 参数选择如下: $A_-$在$[0.002, 0.01]$的范围内随机取值, $A_+$的值通过$A_-$乘以相应的比值得到; (a)中$\tau_-=25$, $\tau_+$分别根据相应的比值计算给出; (b) 中$c_{\text{p}}=1$, $c_{{{\mathrm{d}}}}$分别根据相应的比值计算给出. 每个数据都是5次独立数值计算的平均数; 为了对比, 在图(a), (b)中分别用实线表示$\overline{W}_{\text{s}}=0.5 A_+/A_-$, $\overline{W}_{\text{s}}=A_+/A_-$和$\overline{W}_{{s}}=2 A_+/A_-$的线性关系
Figure 3. Stable average weight $\overline{W}_{\text{s}}$ as a function of $A_+/A_-$: (a) At different ratio $\tau_+/\tau_-$ and $c_{\text{p}}=c_{\text{d}}=1$; (b) at different ratio $c_{\text{p}}/c_{\text{d}}$ and $\tau_+=\tau_-=25$. Here, $A_-$ is given randomly in the range of $0.002$ to $0.01$, $A_+$ is calculated and given by using the ratio of the corresponding parameter. $\tau_-=25$, and $\tau_+$ is calculated and given by using the ratios of the corresponding parameter in panel (a). $c_{\text{p}}=1$, and $c_{\text{d}}$ is calculated and given by using the ratio of the corresponding parameter in panel (b). Data are averaged over 5 independent realizations. For comparison, the solid lines indicating the linear relations $\overline{W}_{\text{s}}=0.5 A_+/A_-$, $\overline{W}_{\text{s}}=A_+/A_-$ and $\overline{W}_{\text{s}}=2 A_+/A_-$ are shown in panels (a) and (b)
图 5 稳定的平均突触权值$\overline{W}_{\text{s}}$与比值$c_{\text{p}}/c_{\text{d}}$的函数关系 (a) $\tau_+=\tau_-=25$固定不变, $A_+/A_-$取不同的比值; (b) $A_+=A_-= $$ 0.006$固定不变, $\tau_+/\tau_-$取不同的比值. 参数选择如下: $c_{\text{d}}$在$[0.5, 2.5]$的范围内随机取值, $c_{\text{p}}$的值通过$c_{\text{d}}$乘以相应的比值得到; (a)中$A_-=0.004$, $A_+$分别根据相应的比值计算给出; (b) 中$\tau_-=25$, $\tau_+$分别根据相应的比值计算给出. 每个数据都是5次独立数值计算的平均数; 为了对比, 在图(a), (b)中分别用实线表示$\overline{W}_{\text{s}}=0.5 c_{\text{p}}/c_{\text{d}}$, $\overline{W}_{\text{s}}= c_{\text{p}}/c_{\text{d}}$和$\overline{W}_{\text{s}}=2 c_{\text{p}}/c_{\text{d}}$的线性关系
Figure 5. Stable average weight $\overline{W}_{\text{s}}$ as a function of $c_{\text{p}}/c_{\text{d}}$: (a) At different ratio $A_+/A_-$ with $\tau_+=\tau_-=25$; (b) at different rations $\tau_+/\tau_-$ with $A_+=A_-=0.006$. $c_{{\rm d}}$ is given randomly in the range of $0.5$ to $2.5$, and $c_{\text{p}}$ is calculated and given by using the ratio of the corresponding parameter. $A_-=0.004$, and $A_+$ is calculated and given by using the ratio of the corresponding parameter in panel (a). $\tau_-=25$, and $\tau_+$ is calculated and given by using the ratio of the corresponding parameter in panel (b). Data are averaged over 5 independent realizations. For comparison, the solid lines indicating the linear relations $\overline{W}_{\text{s}}=0.5 c_{\text{p}}/c_{\text{d}}$, $\overline{W}_{\text{s}}= c_{\text{p}}/c_{\text{d}}$ and $\overline{W}_{\text{s}}=2 c_{\text{p}}/c_{\text{d}}$ are shown in panels (a) and (b)
图 4 稳定的平均突触权值$\overline{W}_{\text{s}}$与比值$\tau_+/\tau_-$的函数关系 (a) $c_{\text{p}}=c_{\text{d}}=1$固定不变, $A_+/A_-$取不同的比值; (b) $A_+=A_-= $$ 0.006$固定不变, $c_{\text{p}}/c_{\text{d}}$取不同的比值. 参数选择如下: $\tau_-$在$[10, 75]$的范围内随机取值, $\tau_+$的值通过$\tau_-$乘以相应的比值得到; (a)中$A_-=0.004$, $A_+$分别根据相应的比值计算给出; (b)中$c_{\text{p}}=1$, $c_{\text{d}}$分别根据相应的比值计算给出. 每个数据都是5次独立数值计算的平均数; 为了对比, 在图(a), (b)中分别用实线表示$\overline{W}_{\text{s}}=0.5\tau_+/\tau_-$, $\overline{W}_{\text{s}}=\tau_+/\tau_-$和$\overline{W}_{\text{s}}=2\tau_+/\tau_-$的线性关系
Figure 4. Stable average weight $\overline{W}_{\text{s}}$ as a function of $\tau_+/\tau_-$: (a) At different ratio $A_+/A_-$ with with $c_{\text{p}}=c_{\text{d}}=1$; (b) at different ratio $c_{\text{p}}/c_{\text{d}}$ with $A_+=A_-=0.006$. $\tau_-$ is given randomly in the range of 10 to 75, $\tau_+$ is calculated and given by using the ratio of the corresponding parameter. $A_-=0.004$, and $A_+$ is calculated and given by using the ratio of the corresponding parameter in panel (a). $c_{\text{p}}=1$, and $c_{\text{d}}$ is calculated and given by using the ratio of the corresponding parameter in panel (b). Data are averaged over 5 independent realizations. For comparison, the solid lines indicating the linear relations $\overline{W}_{\text{s}}=0.5\tau_+/\tau_-$, $\overline{W}_{\text{s}}=\tau_+/\tau_-$ and $\overline{W}_{\text{s}}=2\tau_+/\tau_-$ are shown in panels (a) and (b)
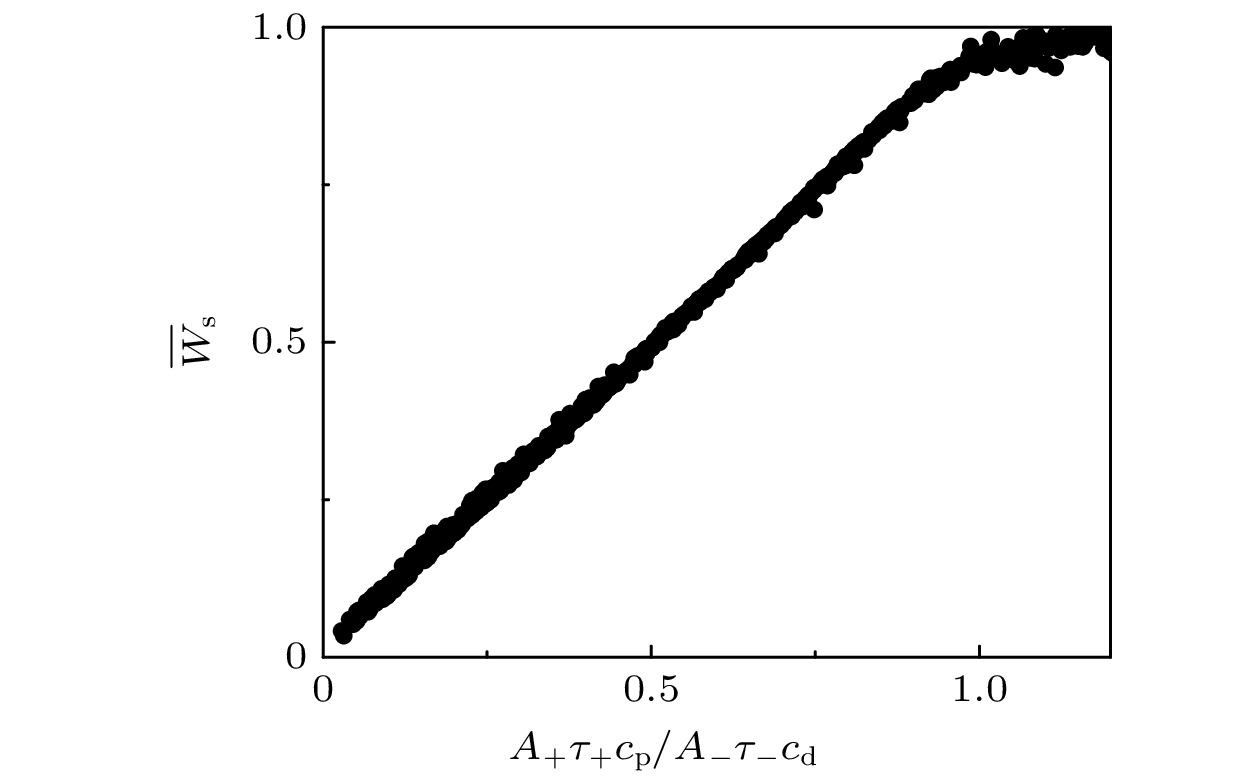
图 6 稳定的平均突触权值$\overline{W}_{{{\mathrm{s}}}}$与比值$A_+\tau_+c_{\text{p}} / A_-\tau_-c_{\text{d}}$的函数关系. 其中$A_+$和$A_-$在$[0.002, 0.01]$范围内随机选取, $\tau_+$和$\tau_-$在$[10, 75]$范围内随机选取, $c_{\text{p}}$和$c_{\text{d}}$在$[0.5, 2.5]$范围内随机选取
Figure 6. Stable average weight $\overline{W}_{{{\mathrm{s}}}}$ as a function of $A_+\tau_+c_{\text{p}}/A_-\tau_-c_{\text{d}}$. Here, $A_+$ and $A_-$ are both chosen randomly in the range of $0.002$ to $0.01$, $\tau_+$ and $\tau_-$ are both chosen randomly in the range of 10 to 75, and $c_{\text{p}}$ and $c_{\text{d}}$ are both chosen randomly in the range of $0.5$ to $2.5$.
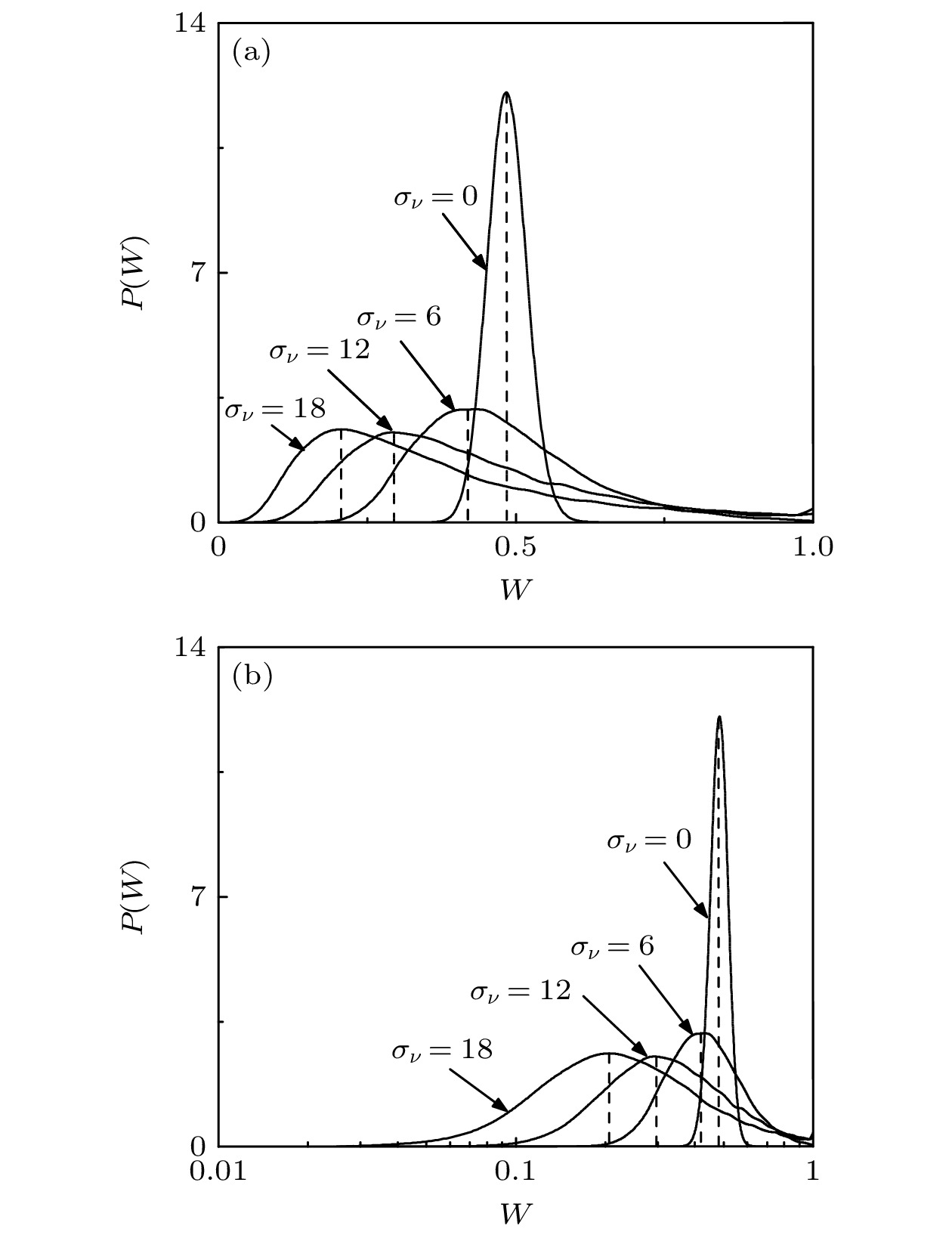
图 7 不同$\sigma_{\nu}$条件下突触权值分布的概率密度$P(W)$ (a) 在线性-线性坐标中; (b) 在对数-线性坐标中. 纵向虚线表示不同$\sigma_{\nu}$的相应最概然权值$W_{\text{p}}$. 参数选择如下: $A_+=A_-= $$ 0.004$, $\tau_+=\tau_-=25$, $c_{\text{p}}=1$和$c_{\text{d}}=2$. 结果是20次数值计算的平均
Figure 7. Probability density $P(W)$ for different $\sigma_{\nu}$ in linear-linear space (a), and in log-linear space (b). The vertical dashed lines indicate the corresponding most probable weights $W_{{{\mathrm{p}}}}$ for different $\sigma_{\nu}$. Here, parameters $A_+ = A_- = $$ 0.004$, $\tau_+=\tau_-=25$, $c_{{{\mathrm{p}}}}=1$ and $c_{{{\mathrm{d}}}}=2$ are given. Results are averaged over 20 realizations.
图 8 稳定的突触权值分布的各特征量与$\sigma_{\nu}$的函数关系 (a) 平均突触权值$\overline{W}_{\text{s}}$和最概然权值$W_{\text{p}}$; (b) 概率密度峰值$P_{\text{p}}$; (c) 突触权值的标准差$\sigma_{W}$和变差系数$CV$. 为了比较, 图(a) 中水平虚线表示用(10)式计算的$\overline{W}_{\text{s}}$的理论值; 垂直虚线表示$\sigma_{\nu}$的临界值. 参数选择如下: $A_+=A_-= $$ 0.004$, $\tau_+=\tau_-=25$, $c_{\text{p}}=1$和$c_{\text{d}}=2$. 结果是20次数值计算的平均
Figure 8. Characteristic quantities of the stable synaptic weight distribution as a function of $\sigma_{\nu}$: (a) The average synaptic weight $\overline{W}_{\text{s}}$ and the most probable weight $W_{\text{p}}$; (b) the most probability density $P_{\text{p}}$; (c) the standard deviation of weight $\sigma_{W}$ and the coefficient of variation $CV$. For comparison, the theoretical value of $\overline{W}_{\text{s}}$ in Eq. (10) is shown by using the horizontal dashed line in panel (a). The vertical dashed line denotes the critical $\sigma_{\nu}$. Here, parameters $A_+=A_-=0.004$, $\tau_+=\tau_-=25$, $c_{\text{p}}=1$ and $c_{\text{d}}=2$ are given. Results are averaged over 20 realizations.
-
[1] Siegel J M 2001 Science 294 1058
Google Scholar
[2] Diekelmann S, Born J 2010 Nat. Rev. Neurosci. 11 114
Google Scholar
[3] Inostroza M, Born J 2013 Annu. Rev. Neurosci. 36 79
Google Scholar
[4] De Lavilléon G, Lacroix M M, Rondi-Reig L, Benchenane K 2015 Nat. Neurosci. 18 493
Google Scholar
[5] Tononi G, Cirelli C 2006 Sleep Med. Rev. 10 49
Google Scholar
[6] Stickgold R, Hobson J A, Fosse R, Fosse M 2001 Science 294 1052
Google Scholar
[7] Tononi G, Cirelli C 2003 Brain Res. Bull. 62 143
Google Scholar
[8] McCormick D A, Feeser H R 1990 Neurosci. 39 103
Google Scholar
[9] Steriade M, Nuñez A, Amzica F 1993 J. Neurosci. 13 3252
Google Scholar
[10] Steriade M, McCormick D A, Sejnowski T J 1993 Science 262 679
Google Scholar
[11] Postnova S, Voigt K, Braun H A 2007 J. Biol. Phys. 33 129
Google Scholar
[12] Zhou J F, Jiang E H, Xu B L, Xu K, Zhou C, Yuan W J 2021 Phys. Rev. E 104 054407
Google Scholar
[13] Dhamala M, Jirsa V K, Ding M 2004 Phys. Rev. Lett. 92 028101
Google Scholar
[14] Nguyen T, Babawale O, Kim T, Jo H J, Liu H, Kim J G 2018 Sci. Rep. 8 16144
Google Scholar
[15] Curtis B J, Williams P G, Jones C R, Anderson J S 2016 Brain Behav. 6 e00576
Google Scholar
[16] Xu B L, Zhou J F, Li R, Jiang E H, Yuan W J 2023 Physica A 617 128663
Google Scholar
[17] Abbott L F, Regehr W G 2004 Nature 431 796
Google Scholar
[18] Destexhe A, Marder E 2004 Nature 431 789
Google Scholar
[19] Caporale N, Dan Y 2008 Annu. Rev. Neurosci. 31 25
Google Scholar
[20] Zhou J F, Yuan W J, Chen D, Wang B H, Zhou Z, Boccaletti S, Wang Z 2019 Phys. Rev. E 99 032419
Google Scholar
[21] Song S, Miller K D, Abbott L F 2000 Nat. Neurosci. 3 919
Google Scholar
[22] Yuan W J, Zhou J F, Zhou C 2013 PLoS One 8 e84644
Google Scholar
[23] Babadi B, Abbott L F 2010 PLoS Comput. Biol. 6 e1000961
Google Scholar
[24] 王美丽, 王峻松 2015 64 108701
Google Scholar
Wang M L, Wang J S 2015 Acta Phys. Sin. 64 108701
Google Scholar
[25] Takahashi Y K, Kori H, Masuda N 2009 Phys. Rev. E 79 051904
Google Scholar
[26] Meisel C, Gross T 2009 Phys. Rev. E 80 061917
Google Scholar
[27] Andrade K C, Spoormaker V I, Dresler M, Wehrle R, Holsboer F, Sämann P G, Czisch M 2011 J. Neurosci. 31 10331
Google Scholar
[28] Hindmarsh J L, Rose R M 1984 Proc. R. Soc. Lond. B Biol. Sci. 221 87
Google Scholar
[29] Erdős P, Rényi A 1960 Publ. Math. Inst. Hung. Acad. Sci. 5 17
[30] Vanvreeswijk C, Sompolinsky H 1996 Science 274 1724
Google Scholar
[31] Vogels T P, Abbott L F 2005 J. Neurosci. 25 10786
Google Scholar
[32] Bi G Q, Poo M 1998 J. Neurosci. 18 10464
Google Scholar
[33] Van Rossum M C W, Bi G Q, Turrigiano G G 2000 J. Neurosci. 20 8812
Google Scholar
[34] McCormick D A 1992 J. Clin. Neurophysiol. 9 212
Google Scholar
[35] Steriade M 2003 Front. Biosci. 8 878
Google Scholar
[36] Li K T, Liang J, Zhou C 2021 Neural Plast. 2021 6668175
Google Scholar
[37] Wang S, Zhou C 2009 Phys. Rev. E 79 061910
Google Scholar
[38] Vyazovskiy V V, Olcese U, Hanlon E C, Nir Y, Cirelli C, Tononi G 2011 Nature 472 443
Google Scholar
[39] Buzsáki G, Mizuseki K 2014 Nat. Rev. Neurosci. 15 264
Google Scholar
[40] Song S, Sjöström P J, Reigl M, Nelson S, Chklovskii D B 2005 PLoS Biol. 3 e68
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 2423
- PDF Downloads: 59
- Cited By: 0
