Enhanced production of <sup>199</sup>Hg cold atoms based on two-dimensional magneto-optical trap

Yu Ze-Xin; Liu Qi-Xin; Sun Jian-Fang; Xu Zhen

doi:10.7498/aps.73.20231243

Abstract

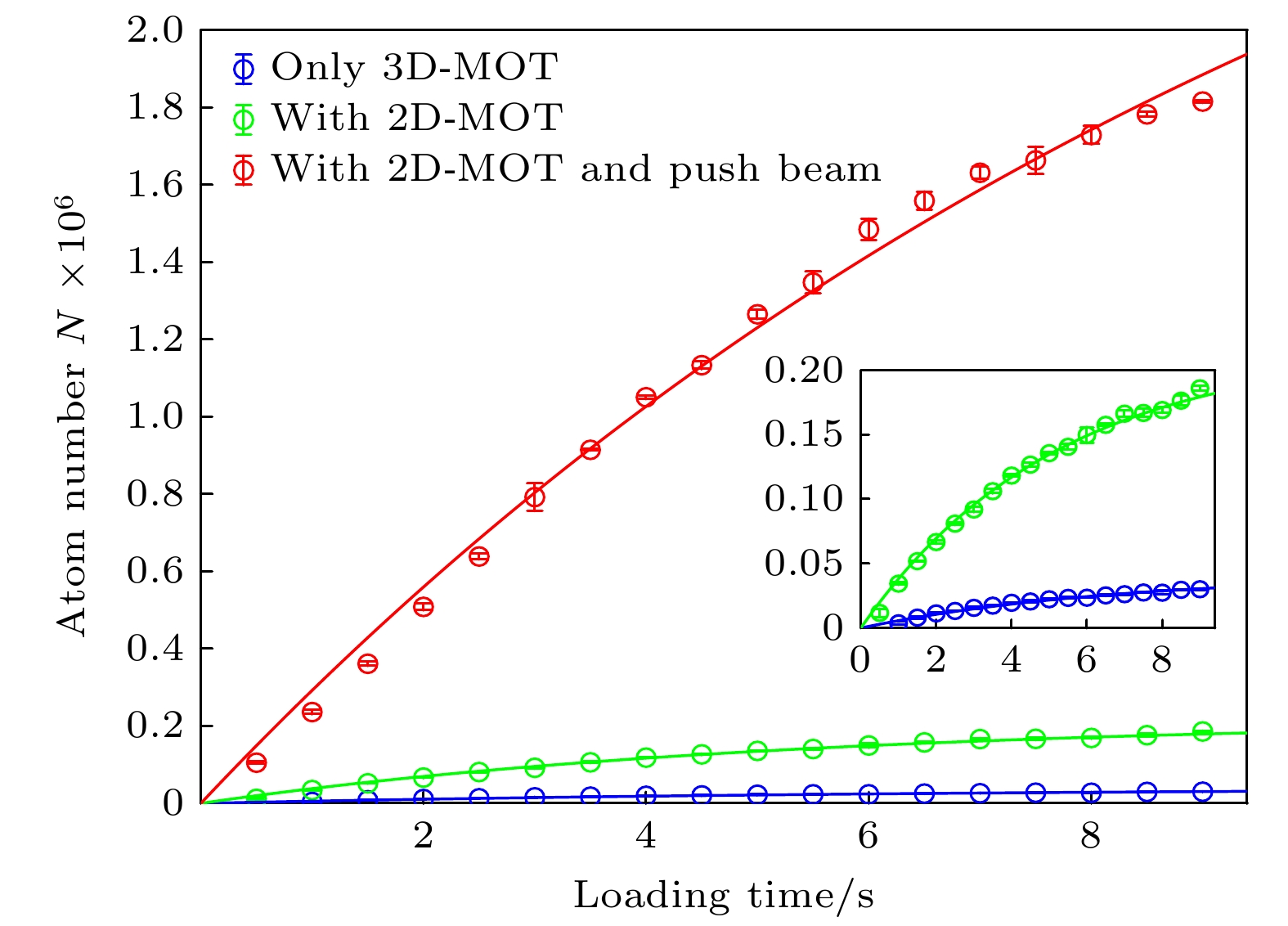
Efficient preparation of cold atoms plays an important role in realizing precision measurement including optical lattice clocks (OLCs). Fast preparation of cold atoms reduces Dick noise by shortening dead time in a clock interrogation cycle, which improves the stability of OLCs. Here, we increase the loading rate of the three-dimensional magneto-optical trap (3D-MOT) in the ultra-high vacuum environment by utilizing the two-dimensional magneto-optical trap (2D-MOT) with a push beam, reduce the temperature of cold atoms with the compression-MOT technique which is implemented by reducing the detuning of 3D-MOT rapidly at the end of atom preparation, and realize the enhanced production of cold atoms for ¹⁹⁹Hg OLCs. To achieve 3D-MOT and 2D-MOT of mercury atoms, a deep ultraviolet laser (DUVL) system composed of three DUVLs is developed with one working in lower power for frequency locking and the other two in high power for laser cooling. Such a configuration improves the long-term frequency stability and shows greater robustness than our previous system consisting of two DUVLs. To maximize the 3D-MOT loading rate, we orderly optimize the detuning and the magnetic field gradient of 3D-MOT and those of 2D-MOT as well as the detuning and the power of the push beam. After all parameters are optimized, we measure the maximum loading rate of 3D-MOT to be 3.1×10⁵ s^–1 and prepare cold atoms of 1.8×10⁶ in 9 s. The loading rate is greatly enhanced by a factor of 51 by using 2D-MOT and the push beam. In order to improve the efficiency of transferring cold atoms from 3D-MOT to optical lattice, we use compression-MOT technique to reduce the temperature of cold atoms and produce cold ¹⁹⁹Hg atoms which are about 45 μK, lower than the expected temperature of Doppler cooling theory. By achieving the high gain of the 3D-MOT loading rate under the ultra-high vacuum and reducing the temperature of cold atoms, this enhanced preparation of cold atoms based on 2D-MOT effectively shortens the preparation time of cold atoms and improves the transfer efficiency of optical lattice, which provides a significant scheme for efficiently preparing cold mercury atoms in other experiments.

Keywords:

Authors and contacts

1.
Key Laboratory of Quantum Optics, Shanghai Institute of Optics and Fine Mechanics, Chinese Academy of Sciences, Shanghai 201800, China
2.
University of Chinese Academy of Sciences, Beijing 100049, China

Corresponding author: Xu Zhen, xuzhen@siom.ac.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant Nos. 11874371, 91436105, 12104474), the Strategic Pilot Science and Technology Project of the Chinese Academy of Science, China (Grant No. XDB21030200), and the Shanghai Science and Technology Program, China (Grant No. 22ZR1471000).

FullText HTML : translate this paragraph

References

[1]	Gross C, Bloch I 2017 Science 357 995 Google Scholar
[2]	Bloch I, Dalibard J, Nascimbène S 2012 Nat. Phys. 8 267 Google Scholar
[3]	Bloch I, Dalibard J, Zwerger W 2008 Rev. Mod. Phys. 80 885 Google Scholar
[4]	Zheng T A, Yang Y A, Wang S Z, Singh J T, Xiong Z X, Xia T, Lu Z T 2022 Phys. Rev. Lett. 129 083001 Google Scholar
[5]	Zheng X, Dolde J, Lochab V, Merriman B N, Li H, Kolkowitz S 2022 Nature 602 425 Google Scholar
[6]	Schioppo M, Brown R C, McGrew W F, Hinkley N, Fasano R J, Beloy K, Yoon T H, Milani G, Nicolodi D, Sherman J A, Phillips N B, Oates C W, Ludlow A D 2017 Nat. Photonics 11 48 Google Scholar
[7]	Al-Masoudi A, Dörscher S, Häfner S, Sterr U, Lisdat C 2015 Phys. Rev. A 92 063814 Google Scholar
[8]	卢晓同, 常宏 2022 光学学报 42 0327004 Google Scholar Lu X T, Chang H 2022 Acta Opt. Sin. 42 0327004 Google Scholar
[9]	Phillips W D, Metcalf H 1982 Phys. Rev. Lett. 48 596 Google Scholar
[10]	Dieckmann K, Spreeuw R J C, Weidemüller M, Walraven J T M 1998 Phys. Rev. A 58 3891 Google Scholar
[11]	Reinaudi G, Osborn C B, Bega K, Zelevinsky T 2012 J. Opt. Soc. Am. B: Opt. Phys. 29 729 Google Scholar
[12]	Jallageas A, Devenoges L, Petersen M, Morel J, Bernier L G, Schenker D, Thomann P, Südmeyer T 2018 Metrologia 55 366 Google Scholar
[13]	Müller T, Wendrich T, Gilowski M, Jentsch C, Rasel E M, Ertmer W 2007 Phys. Rev. A 76 063611 Google Scholar
[14]	Nosske I, Couturier L, Hu F, Tan C, Qiao C, Blume J, Jiang Y H, Chen P, Weidemüller M 2017 Phys. Rev. A 96 053415 Google Scholar
[15]	Schreck F, Druten K V 2021 Nat. Phys. 17 1296 Google Scholar
[16]	Guo C L, Cambier V, Calvert J, Favier M, Andia M, de Sarlo L, Bize S 2023 Phys. Rev. A 107 033116 Google Scholar
[17]	Zhang Y, Liu Q X, Sun J F, Xu Z, Wang Y Z 2022 Chin. Phys. B 31 073701 Google Scholar
[18]	李子亮, 师振莲, 王鹏军 2020 69 126701 Google Scholar Li Z L, Shi Z L, Wang P J 2020 Acta Phys. Sin. 69 126701 Google Scholar
[19]	Yang J L, Long Y, Gao W W, Jin L, Zuo Z C, Wang R Q 2018 Chin. Phys. Lett 35 033701 Google Scholar
[20]	Park S J, Noh J, Mun J 2012 Opt. Commun. 285 3950 Google Scholar
[21]	Barbiero M, Tarallo M G, Calonico D, Levi F, Lamporesi G, Ferrari G 2020 Phys. Rev. Appl. 13 014013 Google Scholar
[22]	Li K, Zhang D F, Gao T Y, Peng S G, Jiang K J 2015 Phys. Rev. A 92 013419 Google Scholar
[23]	Hachisu H, Miyagishi K, Porsev S G, Derevianko A, Ovsiannikov V D, Pal’chikov V G, Takamoto M, Katori H 2008 Phys. Rev. Lett. 100 053001 Google Scholar
[24]	Angstmann E J, Dzuba V A, Flambaum V V 2004 Phys. Rev. A 70 014102 Google Scholar
[25]	Chupp T E, Fierlinger P, Ramsey-Musolf M J, Singh J T 2019 Rev. Mod. Phys. 91 015001 Google Scholar
[26]	Tyumenev R, Favier M, Bilicki S, Bookjans E, Le Targat R, Lodewyck J, Nicolodi D, Le Coq Y, Abgrall M, Guena J, De Sarlo L, Bize S 2016 New J. Phys. 18 113002 Google Scholar
[27]	Yamanaka K, Ohmae N, Ushijima I, Takamoto M, Katori H 2015 Phys. Rev. Lett. 114 230801 Google Scholar
[28]	McFerran J J, Yi L, Mejri S, Bize S 2010 Opt. Lett. 35 3078 Google Scholar
[29]	刘琪鑫, 张晔, 孙剑芳, 徐震 2023 中国激光 50 0701003 Google Scholar Liu Q X, Zhang Y, Sun J F, Xu Z 2023 Chin. J. Lasers 50 0701003 Google Scholar
[30]	Liu H L, Yin S Q, Liu K K, Qian J, Xu Z, Hong T, Wang Y Z 2013 Chin. Phys. B 22 043701 Google Scholar
[31]	苟维, 刘亢亢, 付小虎, 赵儒臣, 孙剑芳, 徐震 2016 65 130201 Google Scholar Gou W, Liu K K, Fu X H, Zhao R C, Sun J F, Xu Z 2016 Acta Phys. Sin. 65 130201 Google Scholar
[32]	Lavigne Q, Groh T, Stellmer S 2022 Phys. Rev. A 105 033106 Google Scholar
[33]	吴长江, 阮军, 陈江, 张辉, 张首刚 2013 62 063201 Google Scholar Wu C J, Ruan J, Chen J, Zhang H, Zhang S G 2013 Acta Phys. Sin. 62 063201 Google Scholar
[34]	Jin S W, Gao J S, Chandrashekara K, Golzhauser C, Schoner J, Chomaz L 2023 Phys. Rev. A 108 023719 Google Scholar
[35]	Dörscher S, Thobe A, Hundt B, Kochanke A, Le Targat R, Windpassinger P, Becker C, Sengstock K 2013 Rev. Sci. Instrum. 84 043109 Google Scholar
[36]	Watson R S, McFerran J J 2021 J. Opt. Soc. Am. B: Opt. Phys. 38 36 Google Scholar
[37]	Lett P D, Phillips W D, Rolston S L, Tanner C E, Watts R N, Westbrook C I 1989 J. Opt. Soc. Am. B: Opt. Phys 6 2084 Google Scholar
[38]	Bjorkholm J E 1988 Phys. Rev. A 38 1599 Google Scholar
[39]	Savard T A, O’Hara K M, Thomas J E 1997 Phys. Rev. A 56 R1095 Google Scholar
[40]	Aldossary O M 2014 J. King Saud Univ. Sci. 26 29 Google Scholar
[41]	Arpornthip T, Sackett C A, Hughes K J 2012 Phys. Rev. A 85 033420 Google Scholar

Cited By

图 1 深紫外激光系统示意图. (DUVL, 深紫外激光器; AOM, 声光调制器; ECDL, 外腔半导体激光器; OPLL, 光学锁相环; SHG, 二次谐波产生; FMS, 调制频率光谱; FA, 光纤放大器; BS, 分束器; PD, 光电二极管; PMF, 保偏光纤; BBO, 偏硼酸钡晶体; QWP, 1/4波片)

Figure 1. Diagram of deep ultraviolet laser system. (DUVL, deep-ultraviolet laser; AOM, acousto-optic modulator; ECDL, external cavity semiconductor laser; OPLL, optical phase-locked loop; SHG, second harmonic generation; FMS, frequency modulation spectroscopy; FA, fiber amplifier; BS, beam splitter; PD, photodiode; PMF, polarization-maintaining fiber; BBO, BaB₂O₄; QWP, quarter-wave plate).

DownLoad: Full-Size Img PowerPoint

图 2 2D-MOT和3D-MOT的实验装置示意图(M, 反射镜; MH, 带孔反射镜; L, 透镜; QWP, 1/4波片; BW, 布儒斯特窗口; EMCCD, 电子倍增电荷耦合器件)

Figure 2. Diagram of experimental setup for 2D-MOT and 3D-MOT (M, mirror; MH, mirror with a hole; L, lens; QWP, quarter-wave plate; BW, Brewster window; EMCCD, electron multiplying charge-coupled device).

DownLoad: Full-Size Img PowerPoint

图 3 (a) 2 s内装载的原子数$ {{N}}_{\text{2s}} $随3D-MOT失谐量$ {{\varDelta }}_{\text{3D}} $与磁场梯度$ \partial{{B}}_{{z}}^{\text{3D}}/\partial{z} $的变化; (b) 2D-MOT横向冷却原子示意图; (c) 1 s内装载的原子数$ {{N}}_{\text{1s}} $随2D-MOT失谐量$ {{\varDelta }}_{\text{2D}} $与磁场梯度$ \partial{{B}}_{{z}}^{\text{2D}}/\partial{z} $的变化; (d) 1 s内装载的原子数$ {{N}}_{\text{1s}} $随推送光的失谐量$ {{\varDelta }}_{\text{push}} $与功率$ {{P}}_{\text{push}} $的变化

Figure 3. (a) Atom number $ {{N}}_{\text{2s}} $ loaded in 2 s varying with detuning $ {{\varDelta }}_{\text{3D}} $ and magnetic gradient field $ \partial{{B}}_{{z}}^{\text{3D}}/\partial{z} $ of 3D-MOT; (b) sketch of 2D-MOT capture process in the transverse direction; (c) atom number $ {{N}}_{\text{1s}} $ loaded in 1 s changing with detuning $ {{\varDelta }}_{\text{2D}} $and magnetic gradient field $ \partial{{B}}_{{z}}^{\text{2D}}/\partial{z} $ of 2D-MOT; (d) atom number $ {{N}}_{\text{1s}} $ loaded in 1 s changing with detuning $ {{\varDelta }}_{\text{push}} $ and power $ {{P}}_{\text{push}} $ of push beam.

DownLoad: Full-Size Img PowerPoint

图 4 ¹⁹⁹Hg在三种不同情况下的冷原子装载曲线, 其中误差棒长度代表标准差

Figure 4. Cold atom loading curves of ¹⁹⁹Hg in three different cases, where error bar denotes standard deviation.

DownLoad: Full-Size Img PowerPoint

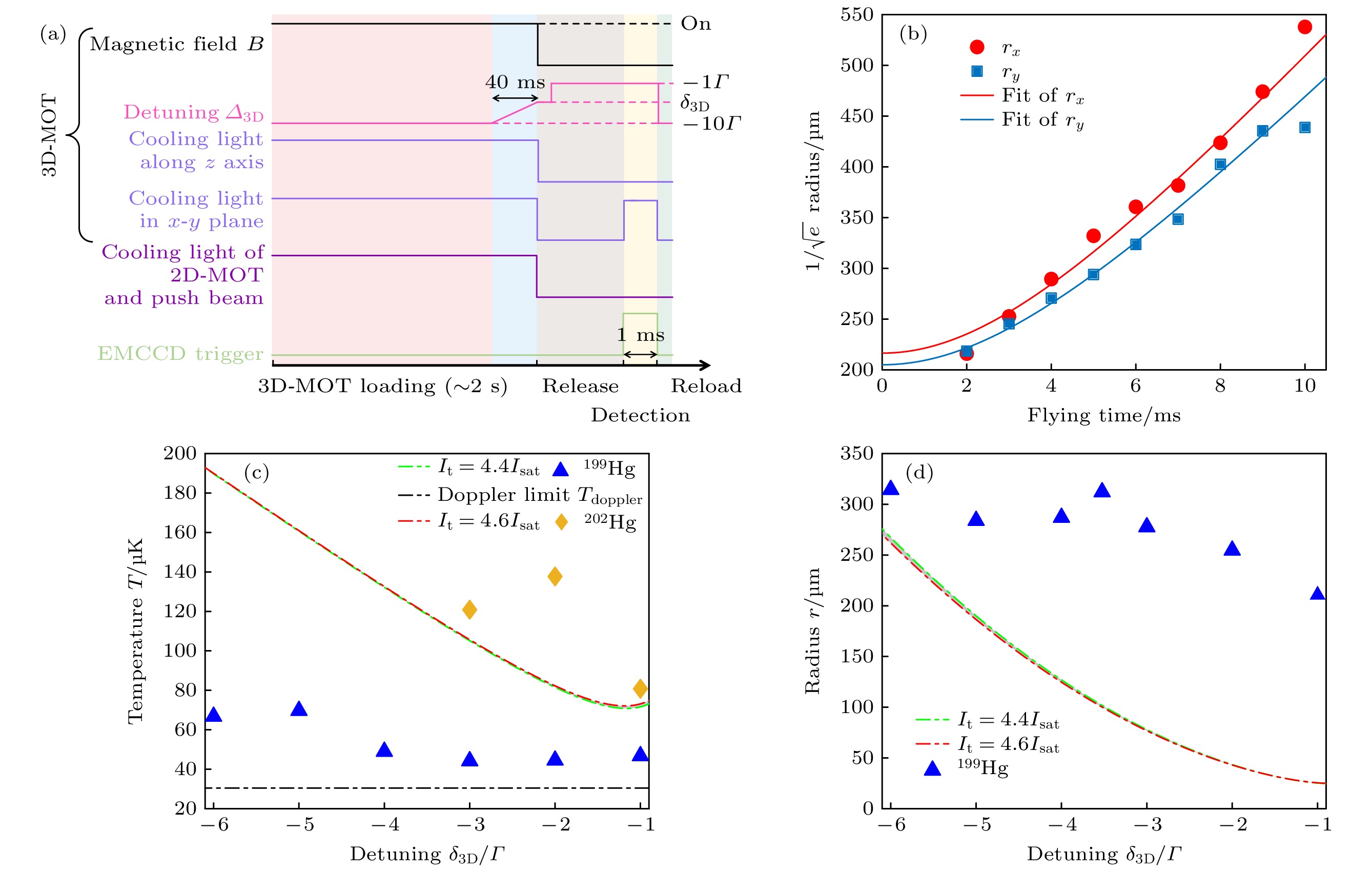
图 5 (a) 压缩磁光阱相关时序; (b) 在失谐量$ {\delta}_{\text{3D}}=-{ \varGamma } $时原子团半径随飞行时间的变化; (c) 原子团温度随失谐量$ {\delta}_{\text{3D}} $的变化; (d) 原子团半径随失谐量$ {\delta}_{\text{3D}} $的变化

Figure 5. (a) Relevant time sequence of compressing MOT; (b) radius of cold atoms varying with flying time at detuning $ {\delta}_{\text{3D}} $ = $ -{ \varGamma } $; (c) temperature of cold atoms varying with detuning $ {\delta}_{\text{3D}} $; (d) radius of cold atoms varying with detuning $ {\delta}_{\text{3D}} $.

DownLoad: Full-Size Img PowerPoint

map

[1]	Gross C, Bloch I 2017 Science 357 995 Google Scholar
[2]	Bloch I, Dalibard J, Nascimbène S 2012 Nat. Phys. 8 267 Google Scholar
[3]	Bloch I, Dalibard J, Zwerger W 2008 Rev. Mod. Phys. 80 885 Google Scholar
[4]	Zheng T A, Yang Y A, Wang S Z, Singh J T, Xiong Z X, Xia T, Lu Z T 2022 Phys. Rev. Lett. 129 083001 Google Scholar
[5]	Zheng X, Dolde J, Lochab V, Merriman B N, Li H, Kolkowitz S 2022 Nature 602 425 Google Scholar
[6]	Schioppo M, Brown R C, McGrew W F, Hinkley N, Fasano R J, Beloy K, Yoon T H, Milani G, Nicolodi D, Sherman J A, Phillips N B, Oates C W, Ludlow A D 2017 Nat. Photonics 11 48 Google Scholar
[7]	Al-Masoudi A, Dörscher S, Häfner S, Sterr U, Lisdat C 2015 Phys. Rev. A 92 063814 Google Scholar
[8]	卢晓同, 常宏 2022 光学学报 42 0327004 Google Scholar Lu X T, Chang H 2022 Acta Opt. Sin. 42 0327004 Google Scholar
[9]	Phillips W D, Metcalf H 1982 Phys. Rev. Lett. 48 596 Google Scholar
[10]	Dieckmann K, Spreeuw R J C, Weidemüller M, Walraven J T M 1998 Phys. Rev. A 58 3891 Google Scholar
[11]	Reinaudi G, Osborn C B, Bega K, Zelevinsky T 2012 J. Opt. Soc. Am. B: Opt. Phys. 29 729 Google Scholar
[12]	Jallageas A, Devenoges L, Petersen M, Morel J, Bernier L G, Schenker D, Thomann P, Südmeyer T 2018 Metrologia 55 366 Google Scholar
[13]	Müller T, Wendrich T, Gilowski M, Jentsch C, Rasel E M, Ertmer W 2007 Phys. Rev. A 76 063611 Google Scholar
[14]	Nosske I, Couturier L, Hu F, Tan C, Qiao C, Blume J, Jiang Y H, Chen P, Weidemüller M 2017 Phys. Rev. A 96 053415 Google Scholar
[15]	Schreck F, Druten K V 2021 Nat. Phys. 17 1296 Google Scholar
[16]	Guo C L, Cambier V, Calvert J, Favier M, Andia M, de Sarlo L, Bize S 2023 Phys. Rev. A 107 033116 Google Scholar
[17]	Zhang Y, Liu Q X, Sun J F, Xu Z, Wang Y Z 2022 Chin. Phys. B 31 073701 Google Scholar
[18]	李子亮, 师振莲, 王鹏军 2020 69 126701 Google Scholar Li Z L, Shi Z L, Wang P J 2020 Acta Phys. Sin. 69 126701 Google Scholar
[19]	Yang J L, Long Y, Gao W W, Jin L, Zuo Z C, Wang R Q 2018 Chin. Phys. Lett 35 033701 Google Scholar
[20]	Park S J, Noh J, Mun J 2012 Opt. Commun. 285 3950 Google Scholar
[21]	Barbiero M, Tarallo M G, Calonico D, Levi F, Lamporesi G, Ferrari G 2020 Phys. Rev. Appl. 13 014013 Google Scholar
[22]	Li K, Zhang D F, Gao T Y, Peng S G, Jiang K J 2015 Phys. Rev. A 92 013419 Google Scholar
[23]	Hachisu H, Miyagishi K, Porsev S G, Derevianko A, Ovsiannikov V D, Pal’chikov V G, Takamoto M, Katori H 2008 Phys. Rev. Lett. 100 053001 Google Scholar
[24]	Angstmann E J, Dzuba V A, Flambaum V V 2004 Phys. Rev. A 70 014102 Google Scholar
[25]	Chupp T E, Fierlinger P, Ramsey-Musolf M J, Singh J T 2019 Rev. Mod. Phys. 91 015001 Google Scholar
[26]	Tyumenev R, Favier M, Bilicki S, Bookjans E, Le Targat R, Lodewyck J, Nicolodi D, Le Coq Y, Abgrall M, Guena J, De Sarlo L, Bize S 2016 New J. Phys. 18 113002 Google Scholar
[27]	Yamanaka K, Ohmae N, Ushijima I, Takamoto M, Katori H 2015 Phys. Rev. Lett. 114 230801 Google Scholar
[28]	McFerran J J, Yi L, Mejri S, Bize S 2010 Opt. Lett. 35 3078 Google Scholar
[29]	刘琪鑫, 张晔, 孙剑芳, 徐震 2023 中国激光 50 0701003 Google Scholar Liu Q X, Zhang Y, Sun J F, Xu Z 2023 Chin. J. Lasers 50 0701003 Google Scholar
[30]	Liu H L, Yin S Q, Liu K K, Qian J, Xu Z, Hong T, Wang Y Z 2013 Chin. Phys. B 22 043701 Google Scholar
[31]	苟维, 刘亢亢, 付小虎, 赵儒臣, 孙剑芳, 徐震 2016 65 130201 Google Scholar Gou W, Liu K K, Fu X H, Zhao R C, Sun J F, Xu Z 2016 Acta Phys. Sin. 65 130201 Google Scholar
[32]	Lavigne Q, Groh T, Stellmer S 2022 Phys. Rev. A 105 033106 Google Scholar
[33]	吴长江, 阮军, 陈江, 张辉, 张首刚 2013 62 063201 Google Scholar Wu C J, Ruan J, Chen J, Zhang H, Zhang S G 2013 Acta Phys. Sin. 62 063201 Google Scholar
[34]	Jin S W, Gao J S, Chandrashekara K, Golzhauser C, Schoner J, Chomaz L 2023 Phys. Rev. A 108 023719 Google Scholar
[35]	Dörscher S, Thobe A, Hundt B, Kochanke A, Le Targat R, Windpassinger P, Becker C, Sengstock K 2013 Rev. Sci. Instrum. 84 043109 Google Scholar
[36]	Watson R S, McFerran J J 2021 J. Opt. Soc. Am. B: Opt. Phys. 38 36 Google Scholar
[37]	Lett P D, Phillips W D, Rolston S L, Tanner C E, Watts R N, Westbrook C I 1989 J. Opt. Soc. Am. B: Opt. Phys 6 2084 Google Scholar
[38]	Bjorkholm J E 1988 Phys. Rev. A 38 1599 Google Scholar
[39]	Savard T A, O’Hara K M, Thomas J E 1997 Phys. Rev. A 56 R1095 Google Scholar
[40]	Aldossary O M 2014 J. King Saud Univ. Sci. 26 29 Google Scholar
[41]	Arpornthip T, Sackett C A, Hughes K J 2012 Phys. Rev. A 85 033420 Google Scholar

[1]	Zhu Yu-Hao, Li Rui. Study of electronic structure and optical transition properties of low-lying excited states of AuB molecules based on configuration interaction method. Acta Physica Sinica, 2024, 73(5): 053101. doi: 10.7498/aps.73.20231347
[2]	Feng Zhuo, Suo Bing-Bing, Han Hui-Xian, Li An-Yang. High-precision electron structure calculation of CaSH molecules and theoretical analysis of its application to laser-cooled target molecules. Acta Physica Sinica, 2024, 73(2): 023301. doi: 10.7498/aps.73.20230742
[3]	Hu Xiao-Hua, Lu Xiao-Tong, Zhang Xiao-Fei, Chang Hong. Density shift measurement and synchronous frequency comparison based on in situ imaging technique. Acta Physica Sinica, 2022, 71(17): 173401. doi: 10.7498/aps.71.20220600
[4]	. Spectroscopic and transition properties of LiCl- anion. Acta Physica Sinica, 2021, (): . doi: 10.7498/aps.70.20211688
[5]	Yin Jun-Hao, Yang Tao, Yin Jian-Ping. Theoretical investigation into spectrum of ${{{\bf{A}}}}^{{\boldsymbol{2}}}{{\boldsymbol{\Pi}} }_{{\boldsymbol{1/2}}}{\boldsymbol{\leftarrow}} {{{\bf{X}}}}^{{\boldsymbol{2}}}{{\boldsymbol{\Sigma}} }_{{\boldsymbol{1/2}}}$ transition for CaH molecule toward laser cooling. Acta Physica Sinica, 2021, 70(16): 163302. doi: 10.7498/aps.70.20210522
[6]	Li Zi-Liang, Shi Zhen-Lian, Wang Peng-Jun. Design and research of two-dimensional magneto-optical trap of sodium atom using permanent magnets. Acta Physica Sinica, 2020, 69(12): 126701. doi: 10.7498/aps.69.20200266
[7]	Wan Ming-Jie, Li Song, Jin Cheng-Guo, Luo Hua-Feng. Theoretical study of laser-cooled SH^– anion. Acta Physica Sinica, 2019, 68(6): 063103. doi: 10.7498/aps.68.20182039
[8]	Wan Ming-Jie, Luo Hua-Feng, Yuan Di, Li Song. Theoretical study of laser cooling of potassium chloride anion. Acta Physica Sinica, 2019, 68(17): 173102. doi: 10.7498/aps.68.20190869
[9]	Chen Tao, Yan Bo. Laser cooling and trapping of polar molecules. Acta Physica Sinica, 2019, 68(4): 043701. doi: 10.7498/aps.68.20181655
[10]	Lin Yi-Ge, Fang Zhan-Jun. Strontium optical lattice clock. Acta Physica Sinica, 2018, 67(16): 160604. doi: 10.7498/aps.67.20181097
[11]	Xing Wei, Sun Jin-Feng, Shi De-Heng, Zhu Zun-Lüe. Theoretical study of spectroscopic properties of 5 -S and 10 states and laser cooling for AlH+ cation. Acta Physica Sinica, 2018, 67(19): 193101. doi: 10.7498/aps.67.20180926
[12]	Chen Liang-Chao, Meng Zeng-Ming, Wang Peng-Jun. Fast production of 87Rb Bose-Einstein condensates. Acta Physica Sinica, 2017, 66(8): 083701. doi: 10.7498/aps.66.083701
[13]	Zhang Yun-Guang, Zhang Hua, Dou Ge, Xu Jian-Gang. Laser cooling of OH molecules in theoretical approach. Acta Physica Sinica, 2017, 66(23): 233101. doi: 10.7498/aps.66.233101
[14]	Gou Wei, Liu Kang-Kang, Fu Xiao-Hu, Zhao Ru-Chen, Sun Jian-Fang, Xu Zhen. Optimization of the loading rate of magneto-optical trap for neutral mercury atom. Acta Physica Sinica, 2016, 65(13): 130201. doi: 10.7498/aps.65.130201
[15]	Wu Chang-Jiang, Ruan Jun, Chen Jiang, Zhang Hui, Zhang Shou-Gang. A two-dimensional magneto-optical trap for a cesium fountain clock. Acta Physica Sinica, 2013, 62(6): 063201. doi: 10.7498/aps.62.063201
[16]	Xu Xin-Ping, Zhang Hai-Chao, Wang Yu-Zhu. A new mini-magnetic lens proposal for coverging the clod atoms. Acta Physica Sinica, 2012, 61(22): 223701. doi: 10.7498/aps.61.223701
[17]	Sun Yu, Feng Gao-Ping, Cheng Cun-Feng, Tu Le-Yi, Pan Hu, Yang Guo-Min, Hu Shui-Ming. Precision spectroscopy of helium using a laser-cooled atomic beam. Acta Physica Sinica, 2012, 61(17): 170601. doi: 10.7498/aps.61.170601
[18]	Zhang Bao-Wu, Zhang Ping-Ping, Ma Yan, Li Tong-Bao. Simulations of one-dimensional transverse laser cooling of Cr atomic beam with Monte Carlo method. Acta Physica Sinica, 2011, 60(11): 113701. doi: 10.7498/aps.60.113701
[19]	Zhang Peng-Fei, Xu Xin-Ping, Zhang Hai-Chao, Zhou Shan-Yu, Wang Yu-Zhu. UV light-induced atom desorption for magnetic trap in single vacuum chamber. Acta Physica Sinica, 2007, 56(6): 3205-3211. doi: 10.7498/aps.56.3205
[20]	Xie Min, Ling Lin, Yang Guo-Jian. Velocity-selective coherent population trapping of a nondegenerate Λ three-level atom. Acta Physica Sinica, 2005, 54(8): 3616-3621. doi: 10.7498/aps.54.3616

Catalog

Vol. 73, Issue 1 - 2024-01-05

Metrics

Abstract views: 2494
PDF Downloads: 78
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板

Enhanced production of ¹⁹⁹Hg cold atoms based on two-dimensional magneto-optical trap

Abstract

Authors and contacts

Corresponding author: Xu Zhen, xuzhen@siom.ac.cn

FullText HTML : translate this paragraph

References

Cited By

Catalog

Metrics

Authors

Referees

About Journal

About

Search

Article

留言板

Enhanced production of 199Hg cold atoms based on two-dimensional magneto-optical trap

Abstract

Authors and contacts

Corresponding author: Xu Zhen, xuzhen@siom.ac.cn

FullText HTML : translate this paragraph

References

Cited By

Catalog

Metrics

Publishing process

Authors

Referees

About Journal

About

Enhanced production of ¹⁹⁹Hg cold atoms based on two-dimensional magneto-optical trap