-
少电子离子束缚态电子g因子的精密测量是借助原子分子体系研究束缚态量子电动力学(QED)理论的有效途径. 特别是在高电荷态重核体系中, 原子核与内壳层电子之间极强的电磁相互作用为研究极端电磁场环境下的QED效应提供了独一无二的条件. 通过精确测量束缚态电子g因子, 还可以分析核效应、测定核结构参数、确定基本物理常数等. 少电子离子束缚态电子g因子的研究已经成为精密谱学方向的前沿课题. 潘宁离子阱(借助稳态电磁场囚禁离子的系统)是进行g因子测量的有效实验装置之一. 本综述将对基于潘宁离子阱开展少电子离子束缚态电子g因子的实验研究进行全面回顾, 介绍基本实验原理与测量方法, 重点论述该领域在近几年中的重要实验成果, 并对未来发展进行简要展望.
The electron g factor is an important fundamental structural parameter in atomic physics, as it reveals various mechanisms of interactions between electrons and external fields. Precise measurements of g factors of bound electrons in simple atomic and molecular systems provide an effective method for investigating the bound-state quantum electrodynamics (QED) theory. Especially in highly-charged heavy ions (HCIs), the strong electromagnetic interactions between the nuclei and inner-shell electrons provide unique opportunities to test QED under extremely strong fields. Accurate measurements of the g factors of the bound-state electrons are also important for determining nuclear effects, nuclear parameters and fundamental constants. The research on g factors of the bound-state electrons has become a frontier topic in fundamental physics. A Penning trap, which uses steady-state electromagnetic fields to confine charged particles, is utilized to precisely measure the g factor. This paper presents a comprehensive review of the experiments on g factors for few-electron simple systems in Penning traps, including experimental principles, experimental setups, measurement methods, and a summary of important research findings. The physical concept of the electron g factor and its historical research background are introduced. The electron g factor is considered as an effective probe to study higher-order QED effects. Through high-precision measurements of the free electron g factor, discrepancies between the fine-structure constants and other experimental results in atomic physics are identified. Notably, the g factor of the 1s electron in HCIs deviates significantly from the value for free electrons as the atomic number increases. Experimental principles, including the principle of the Penning trap and the principle of measuring the bound-state electron g factors are discussed. A double-trap experiment setup and related precision measurement techniques are also introduced. This paper reviews several milestone experiments including (1) the stringent test of bound-state QED by precise measurement of bound-state electron g factor of a 118Sn49+ ion, (2) measurement of the g factors of lithium-like and boron-like ions and their applications, and (3) measurement of the g-factor isotope shift by using an advanced two-ion balance technique in the Penning trap, providing an insight into the QED effects in nuclear recoil. Finally, this paper summarizes the challenges currently faced in measuring the g factors of bound-state electrons in few-electron ion systems and provides the prospects for the future developments of this field. -
Keywords:
- few-electron ions /
- g factor /
- Penning trap /
- precision measurement
[1] Landé A 1921 Z. Für Phys. 5 231
[2] Kusch P, Foley H M 1947 Phys. Rev. 72 1256
[3] Kinoshita T 1990 Advanced Series on Directions in HighEnergy Physics (Singapore: World Scientific) pp218-321
[4] Schwinger J 1948 Phys. Rev. 73 416
Google Scholar
[5] Laporta S, Remiddi E 1996 Phys. Lett. B 379 283
Google Scholar
[6] Aoyama T, Hayakawa M, Kinoshita T, Nio M 2012 Phys. Rev. Lett. 109 111807
Google Scholar
[7] Fan X, Myers T G, Sukra B A D, Gabrielse G 2023 Phys. Rev. Lett. 130 071801
Google Scholar
[8] Shabaev V M, Glazov D A, Plunien G, Volotka A V 2015 J. Phys. Chem. Ref. Data 44 031205
Google Scholar
[9] Breit G 1928 Nature 122 649
[10] Werth G, Sturm S, Blaum K 2018 Adv. At. Mol. Opt. Phys. 67 257
[11] Sturm S, Arapoglou I, Egl A, Höcker M, Kraemer S, Sailer T, Tu B, Weigel A, Wolf R, López-Urrutia J C, Blaum K 2019 Eur. Phys. J. Spec. Top. 227 1425
Google Scholar
[12] Heiße F, Door M, Sailer T, Filianin P, Herkenhoff J, König C M, Kromer K, Lange D, Morgner J, Rischka A, Schweiger C, Tu B, Novikov Y N, Eliseev S, Sturm S, Blaum K 2023 Phys. Rev. Lett. 131 253002
Google Scholar
[13] Morgner J, Tu B, König C M, Sailer T, Heiße F, Bekker H, Sikora B, Lyu C, Yerokhin V A, Harman Z, Crespo López-Urrutia J R, Keitel C H, Sturm S, Blaum K 2023 Nature 622 53
Google Scholar
[14] Brown L S, Gabrielse G 1986 Rev. Mod. Phys. 58 233
Google Scholar
[15] Tu B, Si R, Shen Y, Wang J, Wei B, Chen C, Yao K, Zou Y 2023 Phys. Rev. Res. 5 043014
Google Scholar
[16] Hermanspahn N, Häffner H, Kluge H J, Quint W, Stahl S, Verdú J, Werth G 2000 Phys. Rev. Lett. 84 427
Google Scholar
[17] Sturm S, Wagner A, Schabinger B, Blaum K 2011 Phys. Rev. Lett. 107 143003
Google Scholar
[18] Häffner H, Beier T, Hermanspahn N, Kluge H J, Quint W, Stahl S, Verdú J, Werth G 2000 Phys. Rev. Lett. 85 5308
Google Scholar
[19] Verdú J, Djekić S, Stahl S, Valenzuela T, Vogel M, Werth G, Beier T, Kluge H J, Quint W 2004 Phys. Rev. Lett. 92 093002
Google Scholar
[20] Sturm S, Wagner A, Schabinger B, Zatorski J, Harman Z, Quint W, Werth G, Keitel C H, Blaum K 2011 Phys. Rev. Lett. 107 023002
Google Scholar
[21] Martínez A J G, López-Urrutia J R C, Fischer D, Orts R S, Ullrich J 2007 J. Phys. Conf. Ser. 72 012001
Google Scholar
[22] Zinenko D V, Glazov D A, Kosheleva V P, Volotka A V, Fritzsche S 2023 Phys. Rev. A 107 032815
Google Scholar
[23] Kosheleva V P, Volotka A V, Glazov D A, Zinenko D V, Fritzsche S 2022 Phys. Rev. Lett. 128 103001
Google Scholar
[24] Arapoglou I, Egl A, Höcker M, Sailer T, Tu B, Weigel A, Wolf R, Cakir H, Yerokhin V A, Oreshkina N S, Agababaev V A, Volotka A V, Zinenko D V, Glazov D A, Harman Z, Keitel C H, Sturm S, Blaum K 2019 Phys. Rev. Lett. 122 253001
Google Scholar
[25] Shabaev V M, Glazov D A, Oreshkina N S, Volotka A V, Plunien G, Kluge H J, Quint W 2006 Phys. Rev. Lett. 96 253002
Google Scholar
[26] Yerokhin V A, Berseneva E, Harman Z, Tupitsyn I I, Keitel C H 2016 Phys. Rev. Lett. 116 100801
Google Scholar
[27] Köhler F, Blaum K, Block M, Chenmarev S, Eliseev S, Glazov D A, Goncharov M, Hou J, Kracke A, Nesterenko D A, Novikov Y N, Quint W, Minaya Ramirez E, Shabaev V M, Sturm S, Volotka A V, Werth G 2016 Nat. Commun. 7 10246
Google Scholar
[28] Sailer T, Debierre V, Harman Z, Heiße F, König C, Morgner J, Tu B, Volotka A V, Keitel C H, Blaum K, Sturm S 2022 Nature 606 479
Google Scholar
[29] Debierre V, Keitel C H, Harman Z 2020 Phys. Lett. B 807 135527
Google Scholar
[30] Schneider A, Sikora B, Dickopf S, Müller M, Oreshkina N S, Rischka A, Valuev I A, Ulmer S, Walz J, Harman Z, Keitel C H, Mooser A, Blaum K 2022 Nature 606 878
Google Scholar
[31] Kaiser A, Dickopf S, Door M, Behr R, Beutel U, Eliseev S, Kaushik A, Kromer K, Müller M, Palafox L, Ulmer S, Mooser A, Blaum K 2024 Appl. Phys. Lett. 124 224002
Google Scholar
[32] Devlin J A, Wursten E, Harrington J A, Higuchi T, Blessing P E, Borchert M J, Erlewein S, Hansen J J, Morgner J, Bohman M A, Mooser A H, Smorra C, Wiesinger M, Blaum K, Matsuda Y, Ospelkaus C, Quint W, Walz J, Yamazaki Y, Ulmer S 2019 Phys. Rev. Appl. 12 , 044012 DOI: 10.1103/PhysRevApplied.12.044012
[33] Ketter J, Eronen T, Höcker M, Streubel S, Blaum K 2014 Int. J. Mass Spectrom. 358 1
Google Scholar
[34] Tu B, Hahne F, Arapoglou I, Egl A, Heiße F, Höcker M, König C, Morgner J, Sailer T, Weigel A, Wolf R, Sturm S 2021 Adv. Quantum Technol. 4 2100029
Google Scholar
[35] Bohman M, Grunhofer V, Smorra C, Wiesinger M, Will C, Borchert M J, Devlin J A, Erlewein S, Fleck M, Gavranovic S, Harrington J, Latacz B, Mooser A, Popper D, Wursten E, Blaum K, Matsuda Y, Ospelkaus C, Quint W, Walz J, Ulmer S, BASE Collaboration 2021 Nature 596 514
Google Scholar
[36] Will C, Wiesinger M, Micke P, Yildiz H, Driscoll T, Kommu S, Abbass F, Arndt B P, Bauer B B, Erlewein S, Fleck M, Jäger J I, Latacz B M, Mooser A, Schweitzer D, Umbrazunas G, Wursten E, Blaum K, Devlin J A, Ospelkaus C, Quint W, Soter A, Walz J, Smorra C, Ulmer S 2024 Phys. Rev. Lett. 133 023002
Google Scholar
-
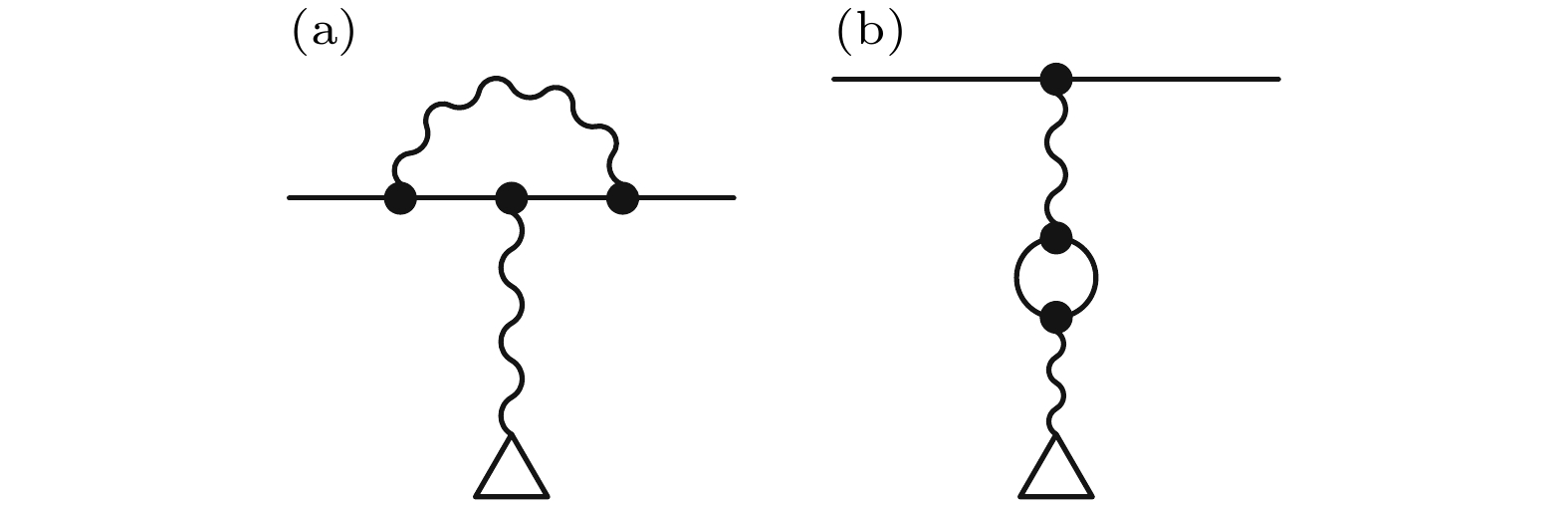
图 1 自由电子g因子最低阶QED修正的费曼图描述, 直线代表自由传播的电子, 三角形表示电磁场而曲线表示电子与电磁场作用中的虚光子 (a)自能效应; (b)真空极化效应
Fig. 1. Feynman diagrams of the first-order QED corrections of the free electron g-factor, the straight line represents the electron, curved lines as the photons and the triangle as the magnetic field: (a) The self-energy term; (b) the vacuum-polarization term.
图 2 类氢离子1s电子g因子与平均电场强度随原子序数Z的依赖关系
Fig. 2. g factor of 1s electron and the mean electromagnetic field as a function of atomic number Z.
图 4 潘宁离子阱剖面结构图, 离子运动与镜像电流测量原理示意图(图中部分素材由马克斯普朗克核物理研究所提供)
Fig. 4. Cut model of Penning traps with illustration of ion motion and image current detection system (some of the materials in the image are provided by the Max-Planck-Institute for Nuclear Physics).
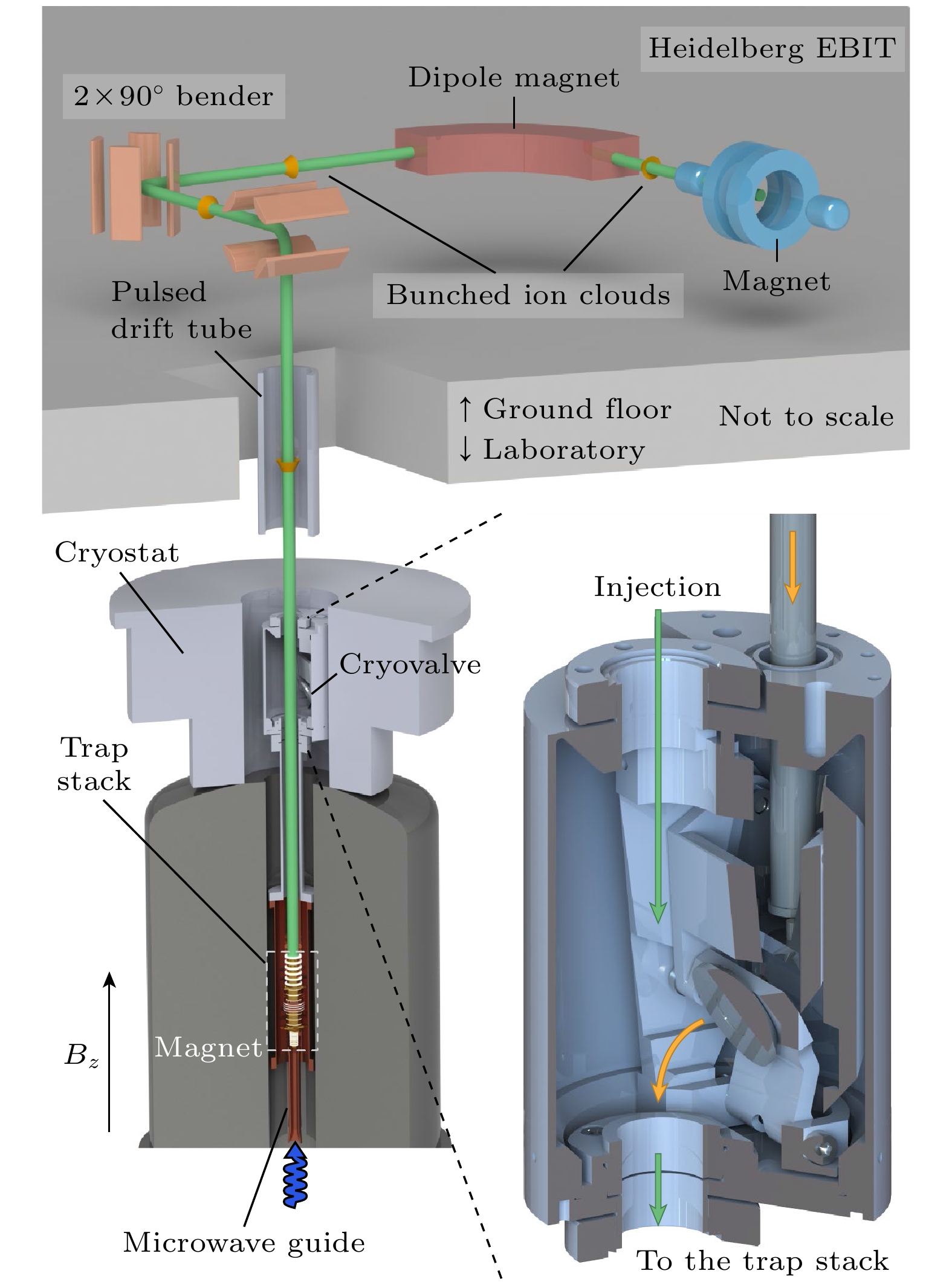
图 8 ALPHATRAP实验系统示意图, 高电荷态重离子由Heidelberg EBIT中产生, 离子束团引出后经过电荷态筛选、偏转、减速、聚焦后被潘宁阱俘获, 手动低温阀可以用来隔离室温束线与低温离子阱的真空环境, 保证离子阱内部真空度优于10–17 torr, 图片来自文献[13]
Fig. 8. Schematic diagram of the ALPHATRAP experiment, the highly charged ions are produced in the Heidelberg EBIT, the ions are extracted, with charge-state selection, and injected into the Penning trap, the cryogenic valve can be closed to isolate the trap vacuum from the beamline, resulting in a vacuum better than 10–17 torr, from Ref. [13].
表 1 类氢12C5+, 16O7+, 20Ne9+, 28Si13+和118Sn49+基态g因子计算与实验数据表
Table 1. Experimental and theoretical g factors of 12C5+, 16O7+, 20Ne9+, 28Si13+和118Sn49+.
12C5+ 16O7+ 20Ne9+ 28Si13+ 118Sn49+ gDirac 1.99872135439(1) 1.99772600306(2) 1.99644517090 1.9930235716 1.90807920530 Free QED 0.00231930437(1) 0.00231930437(1) 0.00231930435 0.00231930437(1) 0.00231930435 BS-QED 0.00000084340(3) 0.00000159438(11) 0.00000265069(12) 0.0000058558(17) 0.000148098(298) FNS 0.00000000041 0.00000000155(1) 0.000 00000476(1) 0.000000 205 0.000014489(24) NR 0.00000008762 0.00000011697 0.00000014641 0.0000002051(1) 0.000000726 Hadronic — — — — –0.000000002 gtheo 2.00104159018(3) 2.00004702128(11) 1.99876727711(12) 1.995348958 0(17) 1.910561821(299) gexp 2.0010415964(45) 2.0000470254(46) 1.99876727699(19) 1.99534895910(81) 1.910562058962(914) 注: gDirac 代表Dirac方程计算的g因子值, Free QED代表自由(电子)QED效应贡献, BS-QED代表束缚态(电子)QED效应贡献, FNS代表核尺寸效应贡献, NR代表核反冲效应贡献, Hadronic代表强子效应贡献. 12C5+, 16O7+, 28Si13数据来自于文献[10], 20Ne9+的数据来自于文献[12], 118Sn49+的数据来自于文献[13]. 
下载: 导出CSV
表 2 28Si11+, 40Ca17+和40Ar13+基态g因子计算与实验数据表
Table 2. Theoretical and experimental g factors of 28Si11+, 40Ca17+ and 40Ar13+.
28Si11+ 40Ca17+ 40Ar13 gDirac 1.9982547533 1.9964260253 0.66377545 QED 0.0023202857 (17) 0.0023216601(17) –0.0007682(4) e-e int. 0.000314 8098 (22) 0.0004542910 (24) 0.0006500(2) FNS + NR 0.0000000436 0.0000000662 –0.0000091(2) gtheo 2.000889 8924 (28) 1.9992020426 (29) 0.6636482 (5) gexp 2.00088988845 (14) 1.9992020405 (11) 0.66364845532(93) 注: QED代表经过屏蔽势修正后的束缚态QED效应, e-e int.代表电子-电子关联效应贡献; 28Si11+与40Ca17+数据来自于文献[23], 40Ar13数据来自于文献[24].
下载: 导出CSV
表 3 20Ne9+和22Ne9+基态g因子差以及相关核效应贡献的计算值, 数据来自文献[28]
Table 3. Contributions of the g-factor difference of 20Ne9+ and 22Ne9+ as well as the experimental result, from Ref. [28]
效应贡献 $ {{\Delta }}g=g\left({}_{}{}^{20}{{\mathrm{N}}{\mathrm{e}}}_{}^{9+}\right)-g\left({}_{}{}^{22}{{\mathrm{N}}{\mathrm{e}}}_{}^{9+}\right) $
($ \times {10}^{-9} $)FNS 0.166(11) Recoil, non-QED 13.2827 Recoil, QED 0.0435 Recoil, (α/π)(me/M) –0.0103 Recoil, (me/M)2 –0.0077 Nuclear polarization 0.0001(3) Δg total theory 13.474(11) Δg experiment 13.47524(53)stat(99)sys
下载: 导出CSV
-
[1] Landé A 1921 Z. Für Phys. 5 231
[2] Kusch P, Foley H M 1947 Phys. Rev. 72 1256
[3] Kinoshita T 1990 Advanced Series on Directions in HighEnergy Physics (Singapore: World Scientific) pp218-321
[4] Schwinger J 1948 Phys. Rev. 73 416
Google Scholar
[5] Laporta S, Remiddi E 1996 Phys. Lett. B 379 283
Google Scholar
[6] Aoyama T, Hayakawa M, Kinoshita T, Nio M 2012 Phys. Rev. Lett. 109 111807
Google Scholar
[7] Fan X, Myers T G, Sukra B A D, Gabrielse G 2023 Phys. Rev. Lett. 130 071801
Google Scholar
[8] Shabaev V M, Glazov D A, Plunien G, Volotka A V 2015 J. Phys. Chem. Ref. Data 44 031205
Google Scholar
[9] Breit G 1928 Nature 122 649
[10] Werth G, Sturm S, Blaum K 2018 Adv. At. Mol. Opt. Phys. 67 257
[11] Sturm S, Arapoglou I, Egl A, Höcker M, Kraemer S, Sailer T, Tu B, Weigel A, Wolf R, López-Urrutia J C, Blaum K 2019 Eur. Phys. J. Spec. Top. 227 1425
Google Scholar
[12] Heiße F, Door M, Sailer T, Filianin P, Herkenhoff J, König C M, Kromer K, Lange D, Morgner J, Rischka A, Schweiger C, Tu B, Novikov Y N, Eliseev S, Sturm S, Blaum K 2023 Phys. Rev. Lett. 131 253002
Google Scholar
[13] Morgner J, Tu B, König C M, Sailer T, Heiße F, Bekker H, Sikora B, Lyu C, Yerokhin V A, Harman Z, Crespo López-Urrutia J R, Keitel C H, Sturm S, Blaum K 2023 Nature 622 53
Google Scholar
[14] Brown L S, Gabrielse G 1986 Rev. Mod. Phys. 58 233
Google Scholar
[15] Tu B, Si R, Shen Y, Wang J, Wei B, Chen C, Yao K, Zou Y 2023 Phys. Rev. Res. 5 043014
Google Scholar
[16] Hermanspahn N, Häffner H, Kluge H J, Quint W, Stahl S, Verdú J, Werth G 2000 Phys. Rev. Lett. 84 427
Google Scholar
[17] Sturm S, Wagner A, Schabinger B, Blaum K 2011 Phys. Rev. Lett. 107 143003
Google Scholar
[18] Häffner H, Beier T, Hermanspahn N, Kluge H J, Quint W, Stahl S, Verdú J, Werth G 2000 Phys. Rev. Lett. 85 5308
Google Scholar
[19] Verdú J, Djekić S, Stahl S, Valenzuela T, Vogel M, Werth G, Beier T, Kluge H J, Quint W 2004 Phys. Rev. Lett. 92 093002
Google Scholar
[20] Sturm S, Wagner A, Schabinger B, Zatorski J, Harman Z, Quint W, Werth G, Keitel C H, Blaum K 2011 Phys. Rev. Lett. 107 023002
Google Scholar
[21] Martínez A J G, López-Urrutia J R C, Fischer D, Orts R S, Ullrich J 2007 J. Phys. Conf. Ser. 72 012001
Google Scholar
[22] Zinenko D V, Glazov D A, Kosheleva V P, Volotka A V, Fritzsche S 2023 Phys. Rev. A 107 032815
Google Scholar
[23] Kosheleva V P, Volotka A V, Glazov D A, Zinenko D V, Fritzsche S 2022 Phys. Rev. Lett. 128 103001
Google Scholar
[24] Arapoglou I, Egl A, Höcker M, Sailer T, Tu B, Weigel A, Wolf R, Cakir H, Yerokhin V A, Oreshkina N S, Agababaev V A, Volotka A V, Zinenko D V, Glazov D A, Harman Z, Keitel C H, Sturm S, Blaum K 2019 Phys. Rev. Lett. 122 253001
Google Scholar
[25] Shabaev V M, Glazov D A, Oreshkina N S, Volotka A V, Plunien G, Kluge H J, Quint W 2006 Phys. Rev. Lett. 96 253002
Google Scholar
[26] Yerokhin V A, Berseneva E, Harman Z, Tupitsyn I I, Keitel C H 2016 Phys. Rev. Lett. 116 100801
Google Scholar
[27] Köhler F, Blaum K, Block M, Chenmarev S, Eliseev S, Glazov D A, Goncharov M, Hou J, Kracke A, Nesterenko D A, Novikov Y N, Quint W, Minaya Ramirez E, Shabaev V M, Sturm S, Volotka A V, Werth G 2016 Nat. Commun. 7 10246
Google Scholar
[28] Sailer T, Debierre V, Harman Z, Heiße F, König C, Morgner J, Tu B, Volotka A V, Keitel C H, Blaum K, Sturm S 2022 Nature 606 479
Google Scholar
[29] Debierre V, Keitel C H, Harman Z 2020 Phys. Lett. B 807 135527
Google Scholar
[30] Schneider A, Sikora B, Dickopf S, Müller M, Oreshkina N S, Rischka A, Valuev I A, Ulmer S, Walz J, Harman Z, Keitel C H, Mooser A, Blaum K 2022 Nature 606 878
Google Scholar
[31] Kaiser A, Dickopf S, Door M, Behr R, Beutel U, Eliseev S, Kaushik A, Kromer K, Müller M, Palafox L, Ulmer S, Mooser A, Blaum K 2024 Appl. Phys. Lett. 124 224002
Google Scholar
[32] Devlin J A, Wursten E, Harrington J A, Higuchi T, Blessing P E, Borchert M J, Erlewein S, Hansen J J, Morgner J, Bohman M A, Mooser A H, Smorra C, Wiesinger M, Blaum K, Matsuda Y, Ospelkaus C, Quint W, Walz J, Yamazaki Y, Ulmer S 2019 Phys. Rev. Appl. 12 , 044012 DOI: 10.1103/PhysRevApplied.12.044012
[33] Ketter J, Eronen T, Höcker M, Streubel S, Blaum K 2014 Int. J. Mass Spectrom. 358 1
Google Scholar
[34] Tu B, Hahne F, Arapoglou I, Egl A, Heiße F, Höcker M, König C, Morgner J, Sailer T, Weigel A, Wolf R, Sturm S 2021 Adv. Quantum Technol. 4 2100029
Google Scholar
[35] Bohman M, Grunhofer V, Smorra C, Wiesinger M, Will C, Borchert M J, Devlin J A, Erlewein S, Fleck M, Gavranovic S, Harrington J, Latacz B, Mooser A, Popper D, Wursten E, Blaum K, Matsuda Y, Ospelkaus C, Quint W, Walz J, Ulmer S, BASE Collaboration 2021 Nature 596 514
Google Scholar
[36] Will C, Wiesinger M, Micke P, Yildiz H, Driscoll T, Kommu S, Abbass F, Arndt B P, Bauer B B, Erlewein S, Fleck M, Jäger J I, Latacz B M, Mooser A, Schweitzer D, Umbrazunas G, Wursten E, Blaum K, Devlin J A, Ospelkaus C, Quint W, Soter A, Walz J, Smorra C, Ulmer S 2024 Phys. Rev. Lett. 133 023002
Google Scholar
下载:
计量
- 文章访问数: 729
- PDF下载量: 39
- 被引次数: 0
