-
在神经系统中, 脑疾病的发生往往对应着神经系统的临界转迁与神经元的异常放电, 因此对临界转迁的早期预警信号(EWS)的研究有助于预测神经元的放电行为, 从而预防脑疾病的发生. 传统EWS, 如自相关系数、方差等指标, 虽然能对动力系统的分岔点进行早期预警, 但其无法对分岔类型进行区分. 而基于功率谱的EWS可以有效预测分岔点并区分分岔类型, 且在气候及生态模型上的预测效果良好. 本文将基于功率谱的EWS应用在神经元系统中, 先后考察了Morris-Lecar和Hindmarsh-Rose模型神经元放电所对应的4种余维一分岔点前的临界现象, 分别计算了传统EWS和基于功率谱的EWS, 并进行对比分析. 结果表明基于功率谱的EWS能有效预测神经元放电, 并且能对不同神经元的I型兴奋和II型兴奋作出区分. 本研究对神经系统的临界转迁的预测有着重要的指导意义, 对神经系统疾病的诊断和治疗有着重要的启示作用.Brain diseases often occur simultaneously with critical changes in neural system and abnormal neuronal firing. Studying the early warning signals (EWSs) of critical changes can provide a promising approach for predicting neuronal firing behaviors, which is conducible to the early diagnosis and prevention of brain diseases. Traditional EWSs, such as autocorrelation and variance, have been widely used to detect the critical transitions in various dynamical systems. However, these methods have limitations in distinguishing different types of bifurcations. In contrast, the EWSs with power spectrum have shown a significant advantage in not only predicting bifurcation points but also distinguishing the types of bifurcations involved. Previous studies have demonstrated its predictive capability in climate and ecological models. Based on this, this study applies the EWS with power spectrum to neuronal systems in order to predict the neuronal firing behaviors and distinguish different classes of neuronal excitability. Specifically, we compute the EWSs before the occurrence of saddle-node bifurcation on the invariant circle and subcritical Hopf bifurcation in the Morris-Lecar neuron model. Additionally, we extend the analysis to the Hindmarsh-Rose model, calculating the EWSs before both saddle-node bifurcation and supercritical Hopf bifurcation. This study contains the four types of codimension-1 bifurcations corresponding to the neuronal firing. For comparison, we also calculate two types of conventional EWSs: lag-1 autocorrelation and variance. In numerical simulations, the stochastic differential equations are simulated by the Euler-Maruyama method. Then, the simulated responses are detrended by the Lowess filter. Finally, the EWSs are calculated by using the rolling window method to ensure the detection of EWS before bifurcation points. Our results show that the EWS with power spectrum can effectively predict the bifurcation points, which means that it can predict neuronal firing activities. Compared with the lag-1 autocorrelation and the variance, the EWSs with power spectrum not only accurately predict the neuronal firing, but also distinguish the classes of excitability in neurons. That is, according to the different characteristics of the power spectrum frequencies, the EWS with power spectrum can effectively distinguish between saddle-node bifurcations and Hopf bifurcations during neuronal firing. This work provides a novel approach for predicting the critical transitions in neural system, with potential applications in diagnosing and treating brain diseases.
-
Keywords:
- neurodynamics /
- power spectrum /
- critical transitions /
- early warning signals
[1] Grziwotz F, Chang C W, Dakos V, et al. 2023 Sci. Adv. 9 eabq4558
 Google Scholar
Google Scholar
[2] Strogatz S H 2018 Nonlinear Dynamics and Chaos: with Applications to Physics, Biology, Chemistry, and Engineering (Boca Raton: CRC Press) pp70–80
[3] Maturana M I, Meisel C, Dell K, et al. 2020 Nat. Commun. 11 2172
 Google Scholar
Google Scholar
[4] Dakos V, Carpenter S R, Brock W A, et al. 2012 PLoS One 7 e41010
 Google Scholar
Google Scholar
[5] Carpenter S R, Brock W A 2006 Ecol. Lett. 9 311
 Google Scholar
Google Scholar
[6] Held H, Kleinen T 2004 Geophys. Res. Lett. 31 L23207
 Google Scholar
Google Scholar
[7] Boettiger C, Hastings A 2012 J. R. Soc. Interface. 9 2527
 Google Scholar
Google Scholar
[8] Scheffer M, Bascompte J, Brock W A, et al. 2009 Nature 461 53
 Google Scholar
Google Scholar
[9] Lade S J, Gross T 2012 PLoS Comput. Biol. 8 e1002360
 Google Scholar
Google Scholar
[10] Carpenter S R, Brock W A 2011 Ecology 92 2196
 Google Scholar
Google Scholar
[11] Bauch C T, Sigdel R, Pharaon J, Anand M 2016 Proc. Natl. Acad. Sci. U. S. A. 113 14560
 Google Scholar
Google Scholar
[12] 颜鹏程, 侯威, 胡经国 2012 61 139202
 Google Scholar
Google Scholar
Yan P C, Hou W, Hu J G 2012 Acta Phys. Sin. 61 139202
 Google Scholar
Google Scholar
[13] 吴浩, 封国林, 侯威, 颜鹏程 2013 62 059202
 Google Scholar
Google Scholar
Wu H, Feng G L, Hou W, Yan P C 2013 Acta Phys. Sin. 62 059202
 Google Scholar
Google Scholar
[14] 吴浩, 侯威, 颜鹏程, 封国林 2012 61 209202
 Google Scholar
Google Scholar
Wu H, Hou W, Yan P C, Feng G L 2012 Acta Phys. Sin. 61 209202
 Google Scholar
Google Scholar
[15] Boers N 2018 Nat. Commun. 9 2556
 Google Scholar
Google Scholar
[16] Meisel C, Klaus A, Kuehn C, Plenz D 2015 PLoS Comput. Biol. 11 e1004097
 Google Scholar
Google Scholar
[17] Dakos V, Van Nes E H, D’Odorico P, Scheffer M 2012 Ecology 93 264
 Google Scholar
Google Scholar
[18] Kuznetsov Y A 2023 Elements of Applied Bifurcation Theory (Cham: Springer International Publishing) pp77–102
[19] Bury T M, Bauch C T, Anand M 2020 J. R. Soc. Interface 17 20200482
 Google Scholar
Google Scholar
[20] Chen Z, Fan P Y, Hou X T, Feng G L, Qian Z H 2024 Chaos Soliton. Fract. 187 115409
 Google Scholar
Google Scholar
[21] Gardiner C W 1985 Handbook of Stochastic Methods for Physics, Chemistry and the Natural Sciences (Berlin: Springer) pp106–107
[22] Box G E, Jenkins G M, Reinsel G C, Ljung G M 2015 Time Series Analysis: Forecasting and Control (Hoboken: John Wiley & Sons) pp21–47
[23] Welch P 1967 IEEE Trans. Audio Electroacoustics 15 70
 Google Scholar
Google Scholar
[24] Prescott S A, De Koninck Y, Sejnowski T J 2008 PLoS Comput. Biol. 4 e1000198
 Google Scholar
Google Scholar
[25] Liu C M, Liu X L, Liu S Q 2014 Biol. Cybern. 108 75
 Google Scholar
Google Scholar
[26] Kendall M G 1938 Biometrika 30 81
 Google Scholar
Google Scholar
[27] Lü M, Wang C N, Ren G D, Ma J, Song X L 2016 Nonlinear Dyn. 85 1479
 Google Scholar
Google Scholar
-
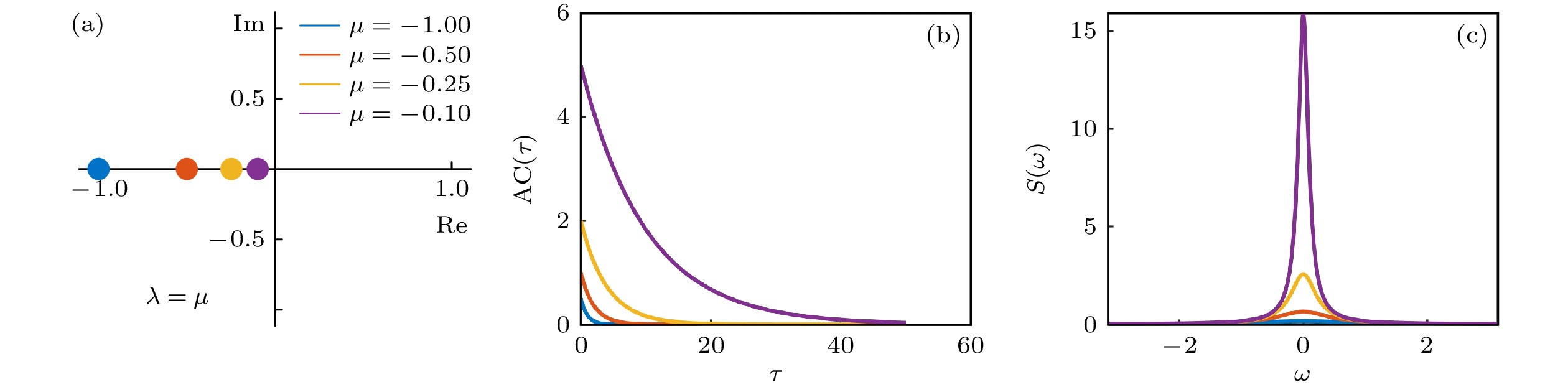
图 1 折叠分岔中自相关和功率谱的近似解析解 (a) 特征值趋近于0; (b) 不同特征值下, 自相关函数随时滞$\tau $的变化; (c) 不同特征值下功率谱的变化
Fig. 1. Approximate analytic solutions for autocorrelation and power spectra in fold bifurcation: (a) The eigenvalue approaching to zero; (b) autocorrelation versus lag $\tau $ under different eigenvalues; (c) variation of power spectrum under different eigenvalues.
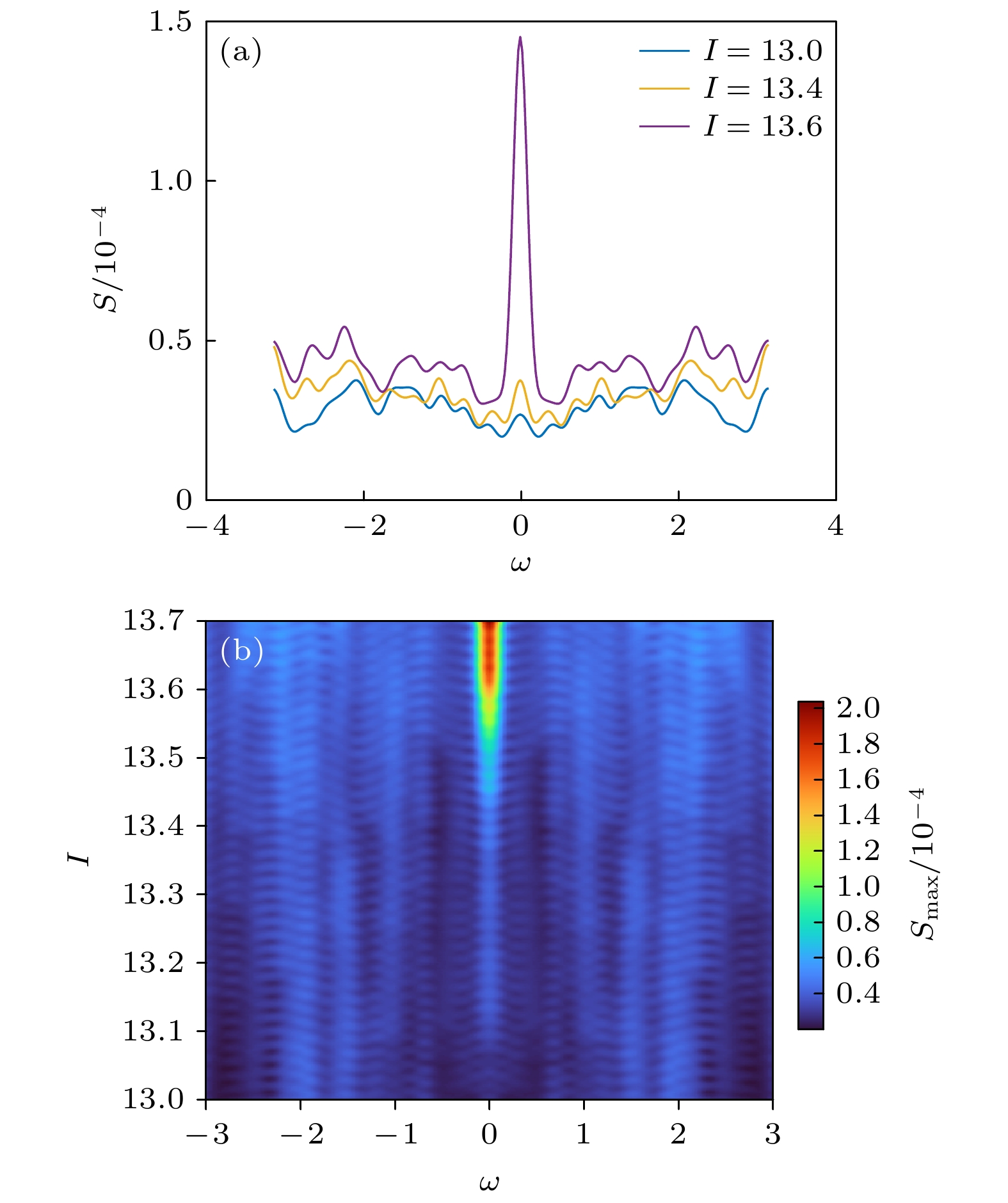
图 2 Hopf分岔中自相关和功率谱的近似解析解 (a) 特征值趋近于0; (b) 不同特征值下, 自相关函数随时滞$\tau $的变化; (c) 不同特征值下功率谱的变化
Fig. 2. Approximate analytic solutions for autocorrelation and power spectra in Hopf bifurcation: (a) Real part of eigenvalues approaching to zero; (b) autocorrelation versus lag $\tau $ under different eigenvalues; (c) variation of power spectrum under different eigenvalues.
-
[1] Grziwotz F, Chang C W, Dakos V, et al. 2023 Sci. Adv. 9 eabq4558
 Google Scholar
Google Scholar
[2] Strogatz S H 2018 Nonlinear Dynamics and Chaos: with Applications to Physics, Biology, Chemistry, and Engineering (Boca Raton: CRC Press) pp70–80
[3] Maturana M I, Meisel C, Dell K, et al. 2020 Nat. Commun. 11 2172
 Google Scholar
Google Scholar
[4] Dakos V, Carpenter S R, Brock W A, et al. 2012 PLoS One 7 e41010
 Google Scholar
Google Scholar
[5] Carpenter S R, Brock W A 2006 Ecol. Lett. 9 311
 Google Scholar
Google Scholar
[6] Held H, Kleinen T 2004 Geophys. Res. Lett. 31 L23207
 Google Scholar
Google Scholar
[7] Boettiger C, Hastings A 2012 J. R. Soc. Interface. 9 2527
 Google Scholar
Google Scholar
[8] Scheffer M, Bascompte J, Brock W A, et al. 2009 Nature 461 53
 Google Scholar
Google Scholar
[9] Lade S J, Gross T 2012 PLoS Comput. Biol. 8 e1002360
 Google Scholar
Google Scholar
[10] Carpenter S R, Brock W A 2011 Ecology 92 2196
 Google Scholar
Google Scholar
[11] Bauch C T, Sigdel R, Pharaon J, Anand M 2016 Proc. Natl. Acad. Sci. U. S. A. 113 14560
 Google Scholar
Google Scholar
[12] 颜鹏程, 侯威, 胡经国 2012 61 139202
 Google Scholar
Google Scholar
Yan P C, Hou W, Hu J G 2012 Acta Phys. Sin. 61 139202
 Google Scholar
Google Scholar
[13] 吴浩, 封国林, 侯威, 颜鹏程 2013 62 059202
 Google Scholar
Google Scholar
Wu H, Feng G L, Hou W, Yan P C 2013 Acta Phys. Sin. 62 059202
 Google Scholar
Google Scholar
[14] 吴浩, 侯威, 颜鹏程, 封国林 2012 61 209202
 Google Scholar
Google Scholar
Wu H, Hou W, Yan P C, Feng G L 2012 Acta Phys. Sin. 61 209202
 Google Scholar
Google Scholar
[15] Boers N 2018 Nat. Commun. 9 2556
 Google Scholar
Google Scholar
[16] Meisel C, Klaus A, Kuehn C, Plenz D 2015 PLoS Comput. Biol. 11 e1004097
 Google Scholar
Google Scholar
[17] Dakos V, Van Nes E H, D’Odorico P, Scheffer M 2012 Ecology 93 264
 Google Scholar
Google Scholar
[18] Kuznetsov Y A 2023 Elements of Applied Bifurcation Theory (Cham: Springer International Publishing) pp77–102
[19] Bury T M, Bauch C T, Anand M 2020 J. R. Soc. Interface 17 20200482
 Google Scholar
Google Scholar
[20] Chen Z, Fan P Y, Hou X T, Feng G L, Qian Z H 2024 Chaos Soliton. Fract. 187 115409
 Google Scholar
Google Scholar
[21] Gardiner C W 1985 Handbook of Stochastic Methods for Physics, Chemistry and the Natural Sciences (Berlin: Springer) pp106–107
[22] Box G E, Jenkins G M, Reinsel G C, Ljung G M 2015 Time Series Analysis: Forecasting and Control (Hoboken: John Wiley & Sons) pp21–47
[23] Welch P 1967 IEEE Trans. Audio Electroacoustics 15 70
 Google Scholar
Google Scholar
[24] Prescott S A, De Koninck Y, Sejnowski T J 2008 PLoS Comput. Biol. 4 e1000198
 Google Scholar
Google Scholar
[25] Liu C M, Liu X L, Liu S Q 2014 Biol. Cybern. 108 75
 Google Scholar
Google Scholar
[26] Kendall M G 1938 Biometrika 30 81
 Google Scholar
Google Scholar
[27] Lü M, Wang C N, Ren G D, Ma J, Song X L 2016 Nonlinear Dyn. 85 1479
 Google Scholar
Google Scholar
计量
- 文章访问数: 3219
- PDF下载量: 59
- 被引次数: 0













 下载:
下载: