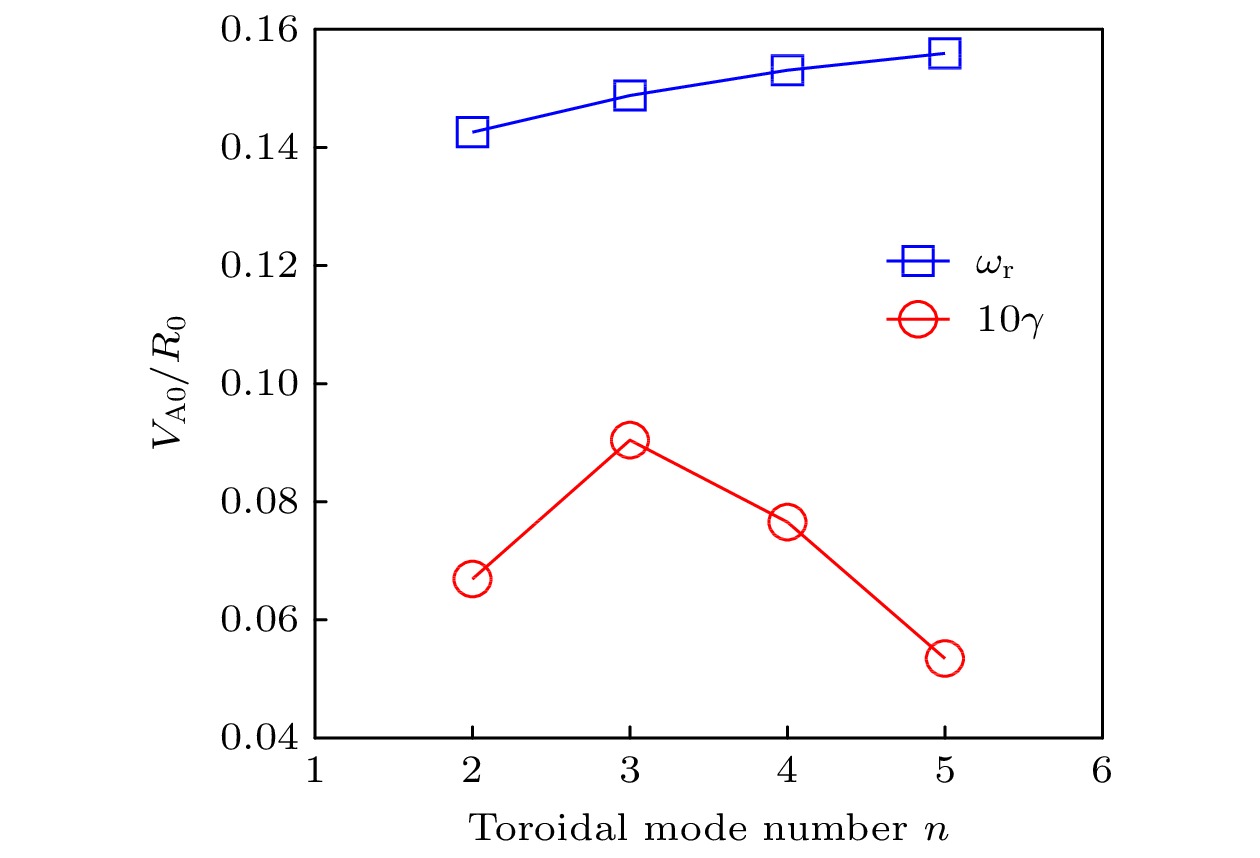
-
The energetic electron (EE) excitation of beta-induced Alfvén eigenmodes is investigated by using the newly developed global eigenvalue code MAS, which is based on a hybrid model that consists of Landau fluid bulk plasma and drift kinetic EE. Specifically, the bulk plasma kinetic effects such as finite Larmor radius, diamagnetic drifts and Landau dampings, and the EE adiabatic fluid response of convection and non-adiabatic kinetic response of precessional drift resonance are incorporated in the simulations. The global eigenmode equation is solved for e-BAE mode structure and linear dispersion relation in tokamak non-perturbatively. The radial width of e-BAE mode structure becomes narrower as the toroidal mode number increases, which can be explained by the change of Alfvén continuous spectra that interact with kinetic Alfvén waves for corresponding eigenmode formation. The e-BAE growth rate exhibits a non-monotonic variation with toroidal mode number for precessional drift resonance destabilization, while the e-BAE real frequency is close to the continuum accumulation point that almost remains the same. The parametric dependence of e-BAE stability on EE density and that on temperature are analyzed by MAS non-perturbative simulations, which shows that the EE density can affect e-BAE real frequency and thus changes the resonance condition, resulting in e-BAE stabilization in the strong EE drive regime. Further, the EE non-perturbative effect on the symmetry breaking of e-BAE mode structure is reported. The poloidal symmetry breaking characterized by the ‘boomerang’ shape two-dimensional (2D) structure can be greatly enhanced by increasing EE temperature, together with the large radial variation of the poloidal phase angle of dominant principal poloidal harmonic. The radial symmetry breaking of e-BAE mode structure arises when EE density/temperature drive is not symmetric with respect to corresponding rational surface, which can lead to a net volume-averaged value of e-BAE parallel wave number which drives plasma intrinsic rotation. These results are helpful in understanding the e-BAE dynamics observed in recent experiments.
-
Keywords:
- energetic electron /
- beta-induced Alfvén eigenmode /
- non-perturbative effect /
- symmetry breaking
[1] Fasoli A, Gormenzano C, Berk H L, Breizman B, Briguglio S, Darrow D S, Gorelenkov N, Heidbrink W W, Jaun A, Konovalov S V, Nazikian R, Noterdaeme J M, Sharapov S, Shinohara K, Testa D, Tobita K, Todo T, Vlad G, Zonca F 2007 Nucl. Fusion 47 S264
Google Scholar
[2] Chen L, Zonca F, 2016 Rev. Mod. Phys. 88 015008
Google Scholar
[3] Heidbrink W W 2008 Phys. Plasmas 15 055501
Google Scholar
[4] Heidbrink W W 2020 Phys. Plasmas 27 030901
Google Scholar
[5] Chen W, Ding X T, Yang Q W, Liu Y, Ji X Q, Zhang Y P, Zhou J, Yuan G L, Sun H J, Li W, Zhou Y, Huang Y, Dong J Q, Feng B B, Song X M, Shi Z B, Liu Z T, Song X Y, Li L C, Duan X R, Liu Y 2010 Phys. Rev. Lett. 105 185004
Google Scholar
[6] Zhao N, Bao J, Chen W, Shi T H, Wang Z X, Yan N, Liu S C, Liu H Q, Zang Q, Lin S Y, Wu X H, Chu Y Q, Wang Y M, Wang S X, Hu W H, Chu N, Li M H, Zhai X M, Jie Y X, Jiang M, Lin X D, Gao X 2021 Nucl. Fusion 61 046013
Google Scholar
[7] Zonca F, Buratti P, Cardinali A, Chen L, Dong J Q, Long Y X, Milovanov A V, Romanelli F, Smeulders P, Wang L, Wang Z T, Castaldo C, Cesario R, Giovannozzi E, Marinucci M, Ridolfini V Pericoli 2007 Nucl. Fusion 47 1588
Google Scholar
[8] Ma R R, Qiu Z Y, Li Y Y, Chen W 2020 Nucl. Fusion 60 056019
Google Scholar
[9] Ma R R, Qiu Z Y, Li Y Y, Chen W 2021 Nucl. Fusion 61 036014
Google Scholar
[10] Cheng J Y, Zhang W L, Lin Z, Holod I, Li D, Chen Y, Cao J T 2016 Phys. Plasmas 23 052504
Google Scholar
[11] Wang J L, Todo Y, Wang H, Wang Z-X 2020 Nucl. Fusion 60 112012
Google Scholar
[12] Qiu Z Y, Chen L, Zonca F, Ma R R 2020 Plasma Phys. Control. Fusion 62 105012
Google Scholar
[13] Connor J, Hastie R J, Taylor J B 1979 Proc. Roy. Soc. London A 365 1720
[14] Lee W W, Lewandowski J L V, Hahm T S, Lin Z 2001 Phys. Plasmas 8 4435
Google Scholar
[15] Bao J, Zhang W L, Li D, Lin Z, Dong G, Liu C, Xie H S, Meng G, Cheng J Y, Dong C, Cao J T 2023 Nucl. Fusion 63 076021
Google Scholar
[16] Bao J, Zhang W L, Li D, Lin Z, Qiu Z Y, Chen W, Zhu X, Cheng J Y, Dong C, Cao J T 2023 Nucl. Fusion DOI: 10.1088/1741-4326/ad0598
[17] Bao J, Zhang W L, Li D, Lin Z 2020 J. Fusion Energ. 39 382
Google Scholar
[18] Zonca F, Chen L, Santoro R A 1996 Plasma Phys. Control. Fusion 38 2011
Google Scholar
[19] Wang X, Zonca F, Chen L 2010 Plasma Phys. Control. Fusion 52 115005
Google Scholar
[20] Ma R R, Zonca F, Chen L 2015 Phys. Plasmas 22 092501
Google Scholar
[21] Lu Z X, Wang X, Lauber Ph, Zonca F 2018 Nucl. Fusion 58 082021
Google Scholar
[22] Cheng C Z 1992 Phys. Rep. 211 1
Google Scholar
[23] Heidbrink W W, Hansen E C, Austin M E, Kramer G J, van Zeeland M A 2022 Nucl. Fusion 62 066020
Google Scholar
[24] Wang Z X, Lin Z, Holod I, Heidbrink W W, Tobias B, van Zeeland M, Austin M E 2013 Phys. Rev. Lett. 111 145003
Google Scholar
[25] Liu Y Q, Lin Z, Zhang H S, Zhang W L 2017 Nucl. Fusion 57 114001
Google Scholar
[26] Diamond P H, Kosuga Y, Gürcan Ö D, McDevitt C J, Hahm T S, Fedorczak N, Rice J E, Wang W X, Ku S, Kwon J M, Dif-Pradalier G, Abiteboul J, Wang L, Ko W H, Shi Y J, Ida K, Solomon W, Jhang H, Kim S S, Yi S, Ko S H, Sarazin Y, Singh R, Chang C S 2013 Nucl. Fusion 53 104019
Google Scholar
[27] Dong G, Wei X, Bao J, Brochard G, Lin Z, Tang W M 2021 Nucl. Fusion 61 126061
Google Scholar
-
图 1 模拟采用的平衡参数(其中
$ {\psi _{\text{T}}} $ 表示归一化环向磁通) (a)安全因子$ q $ 和磁剪切$ s=\dfrac{1}{q}\dfrac{{\rm{d}}q}{{\rm{d}}r} $ 剖面; (b)高能量电子密度$ {n}_{{\rm{h}}0} $ 及其梯度特征长度$ {L}_{{\rm{n}}, {\rm{h}}}^{-1}=\dfrac{1}{{n}_{{\rm{h}}0}}\dfrac{{\rm{d}}{n}_{{\rm{h}}0}}{{\rm{d}}r} $ 剖面Figure 1. Simulation equilibrium parameters: (a) Radial profiles of safety factor
$ q $ and magnetic shear$ s=\dfrac{1}{q}\dfrac{{\rm{d}}q}{{\rm{d}}r} $ ; (b) radial profiles of energetic electron density$ {n}_{{\rm{h}}0} $ and corresponding gradient scale length$ {L}_{{\rm{n}}, {\rm{h}}}^{-1}=\dfrac{1}{{n}_{{\rm{h}}0}}\dfrac{{\rm{d}}{n}_{{\rm{h}}0}}{{\rm{d}}r} $ .
图 2 (a)—(d)环向模数
$ n=2 $ ,$ n=3 $ ,$ n=4 $ 和$ n=5 $ 的连续谱, 其中细线代表声波, 粗线代表阿尔芬波, 彩色代表归一化的e-BAE振幅强弱; 纵轴刻度单位是$ V_{\rm A0}/R_0 $ (即磁轴处阿尔芬频率), 其中$ V_{\rm A0} = B_{0,{\rm a}}/\sqrt {4\pi {n_{{\rm i0},{\rm a}}}{m_{\rm i}}} $ 为磁轴处阿尔芬速度,$ {R_0} $ 为磁轴处大半径, B0,a为磁轴处磁场, ni0,a为磁轴处离子密度Figure 2. (a)–(d) Continuous spectra of toroidal mode numbers
$ n=2 $ ,$ n=3 $ ,$ n=4 $ and$ n=5 $ , where the thin line represents the acoustic branch, the thick line represents the Alfvénic branch, and the colorbar represents the normalized radial amplitude of e-BAE.
图 3 (a1)—(d1)环向模数
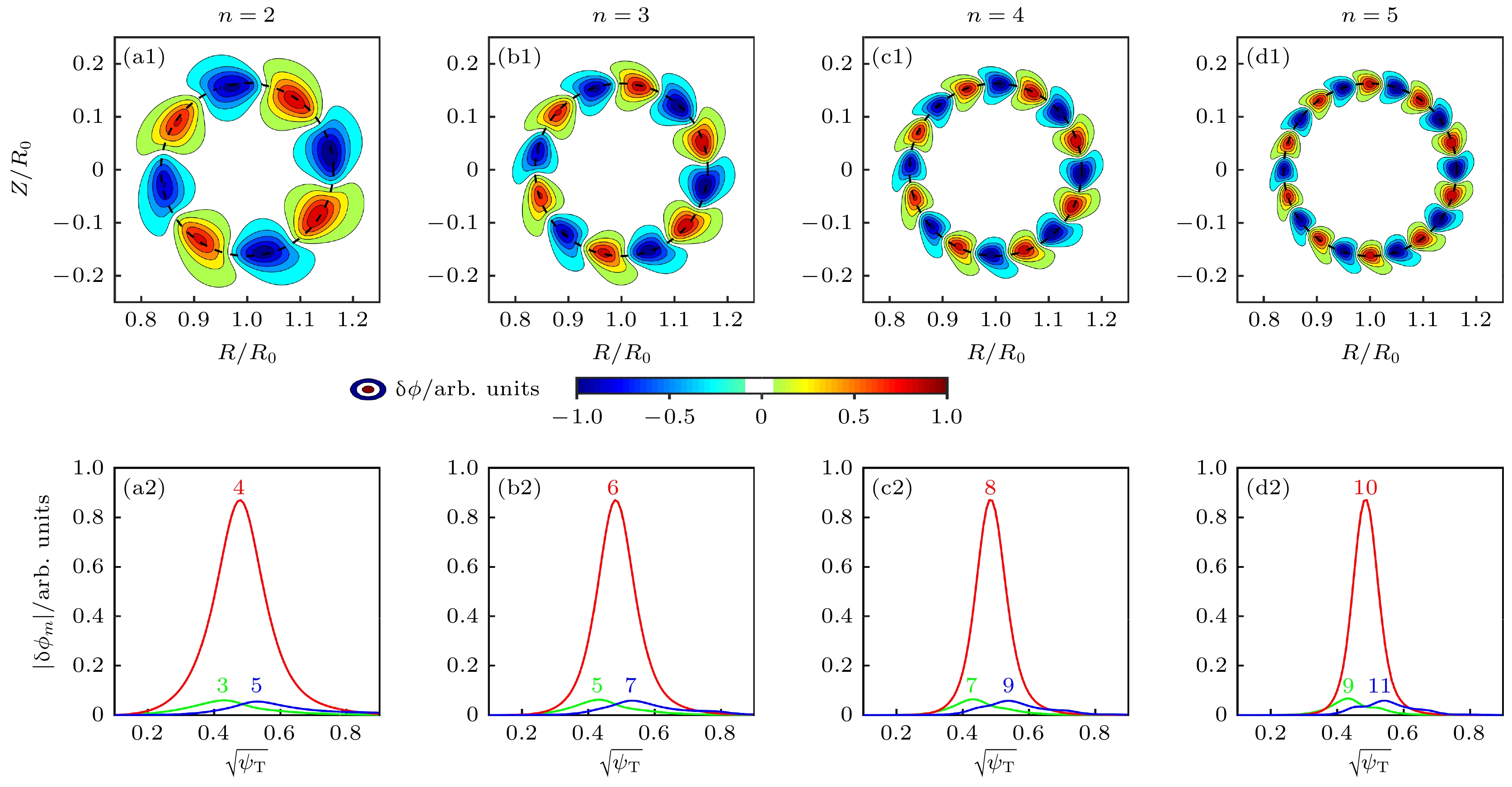
$ n=2 $ ,$ n=3 $ ,$ n=4 $ 和$ n=5 $ 的e-BAE静电势$ {\text{δ}} \phi $ 二维模结构; (a2)—(d2)各极向傅里叶分量剖面Figure 3. (a1)–(d1) The 2D poloidal mode structures of electrostatic potential
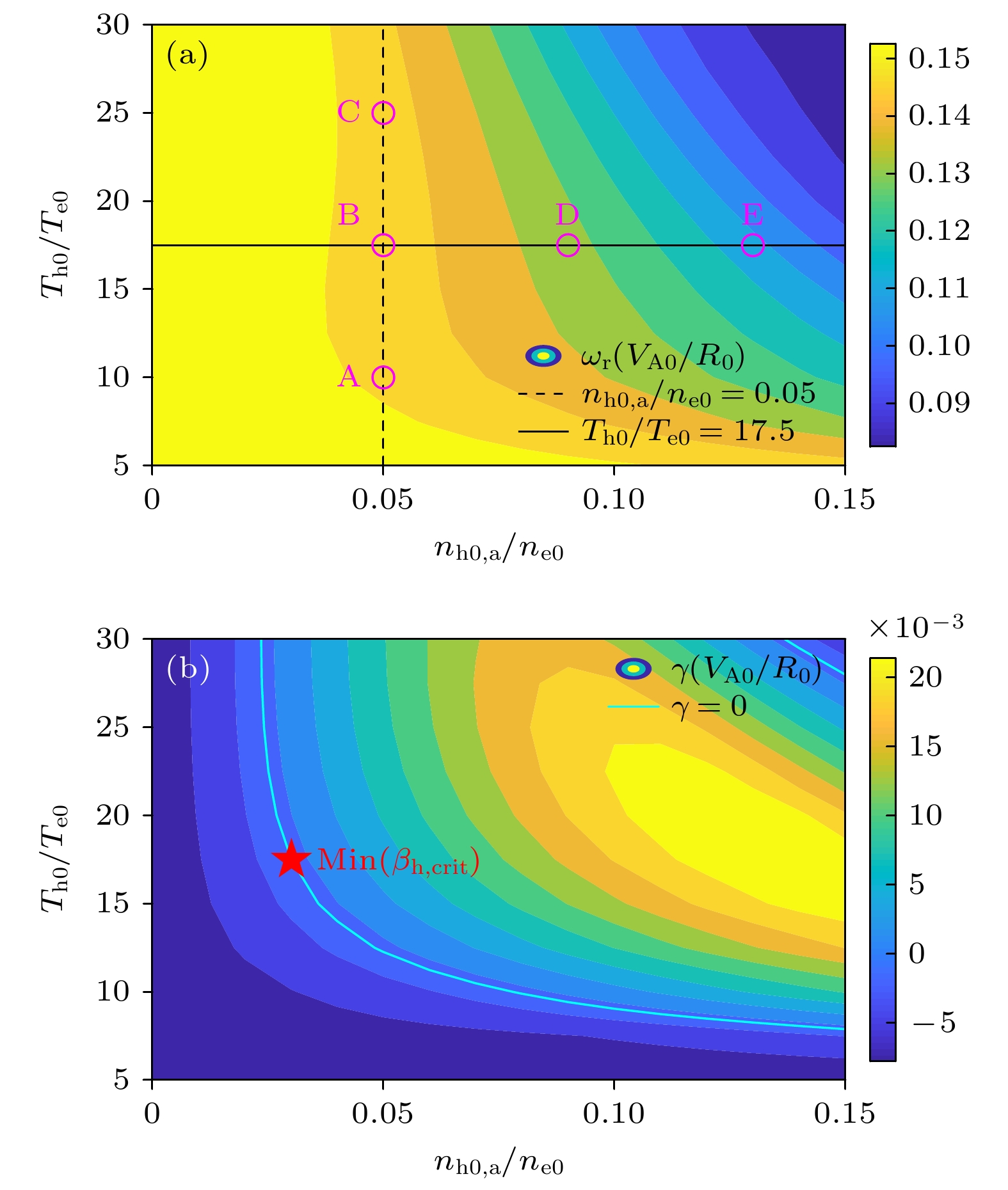
$ {\text{δ}} \phi $ of toroidal mode numbers$ n=2 $ ,$ n=3 $ ,$ n=4 $ and$ n=5 $ ; (a2)–(d2) radial profiles of each poloidal harmonics.
图 4 e-BAE实频率和增长率随环向模数
$ n $ 的变化, 其中纵轴刻度单位是$V_{\rm A0}/R_0 $ (即磁轴处阿尔芬频率)Figure 4. The e-BAE real frequency and growth rate dependences on the toroidal mode number
$ n $ .
图 5 e-BAE (a)实频率和(b)增长率随高能量电子密度和温度的依赖关系. A—E为参数空间下的5个代表算例, 用于下一步模结构分析. 青蓝色实线为e-BAE临界不稳定边界
$ (\gamma =0) $ , 五角星为激发e-BAE需要的最小高能量电子比压对应的密度和温度值Figure 5. The e-BAE (a) real frequency and (b) growth rate dependences on energetic electron (EE) density and temperature. A—E are five typical cases for next mode structure analysis. Cyan solid line represents the boundary of marginal stable e-BAEs with
$ \gamma =0 $ , and the pentagram marks the EE density and temperature locations of the minimal value of EE$ {\beta }_{{\rm{h}}} $ required for e-BAE excitation.
图 6 (a1)—(c1)图5中A, B, C算例的静电势
$ {\text{δ}} \phi $ 二维模结构; (a2)—(c2) A, B, C算例中主极向分量$ {\text{δ}} {\phi }_{m=6} $ 及其相位角$ {\theta }_{{\rm{r}}}= {\rm{a}}{\rm{r}}{\rm{c}}{\rm{t}}{\rm{a}}{\rm{n}}\dfrac{ {\rm{Im}} ({\text{δ}} {\phi }_{m=6}) } {{\rm{R}}{\rm{e}}({\text{δ}} {\phi }_{m=6} ) }$ 的径向剖面, 灰色阴影部分表示e-BAE有限振幅区域Figure 6. (a1)–(c1) The 2D poloidal mode structures of electrostatic potential
$ {\text{δ}} \phi $ for cases A, B and C in Fig. 5; (a2)–(c2) the radial profiles of dominant principal poloidal harmonic of$ {\text{δ}} {\phi }_{m=6} $ and corresponding phase angle$ {\theta }_{{\rm{r}}}= {\rm{a}}{\rm{r}}{\rm{c}}{\rm{t}}{\rm{a}}{\rm{n}}\dfrac{ {\rm{Im}} ({\text{δ}} {\phi }_{m=6}) } {{\rm{R}}{\rm{e}}({\text{δ}} {\phi }_{m=6} ) } $ , and the gray shaded region represents the radial domain with finite e-BAE amplitude.
图 7 (a1)—(c1)图5中B, D, E算例的静电势
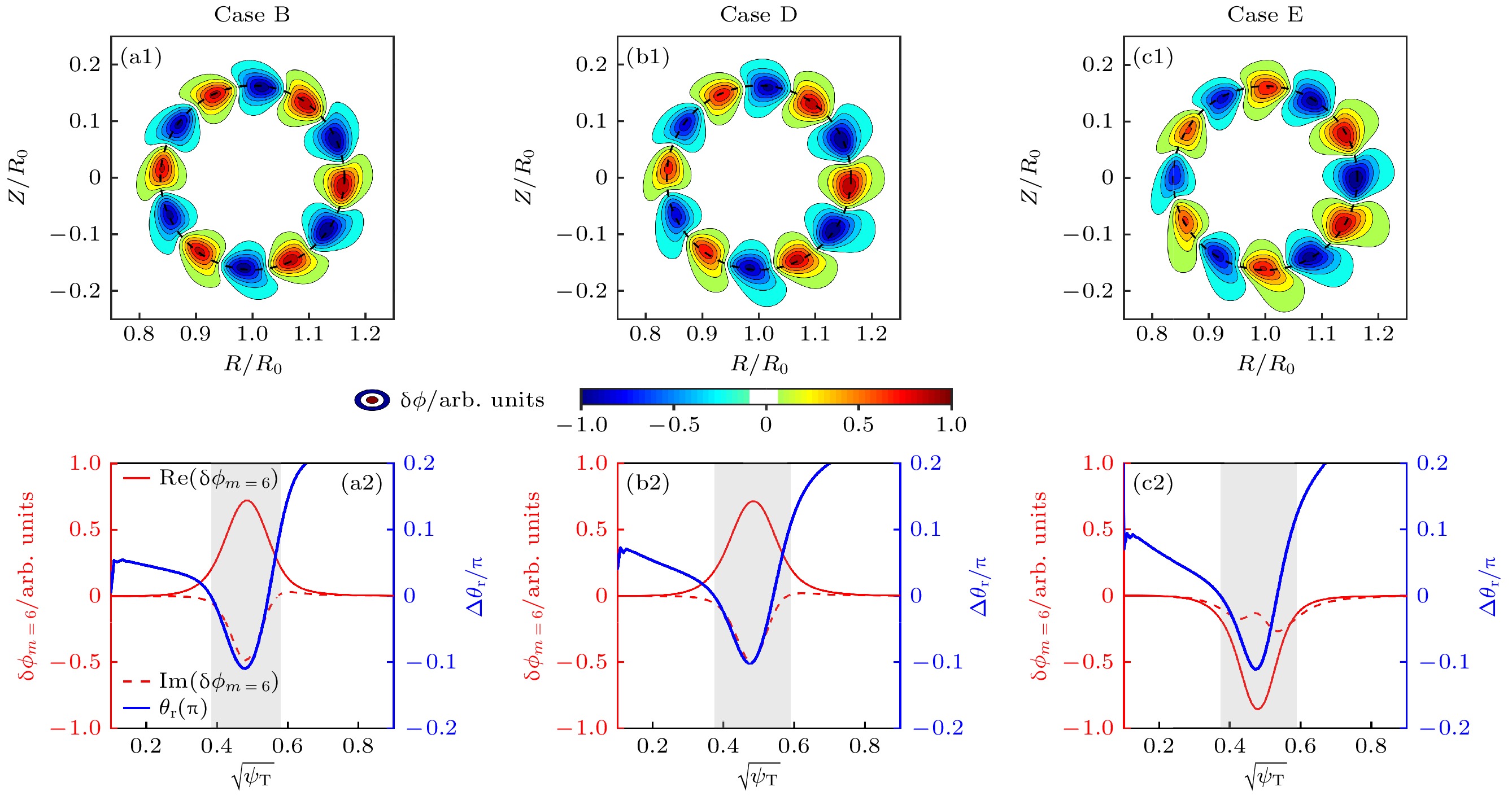
$ {\text{δ}} \phi $ 二维模结构; (a2)—(c2) B, D, E算例中主极向分量$ {\text{δ}} {\phi }_{m=6} $ 及其相位角$ {\theta }_{{\rm{r}}}= {\rm{a}}{\rm{r}}{\rm{c}}{\rm{t}}{\rm{a}}{\rm{n}}\dfrac{ {\rm{Im}} ({\text{δ}} {\phi }_{m=6}) } {{\rm{R}}{\rm{e}}({\text{δ}} {\phi }_{m=6} ) } $ 的径向剖面, 灰色阴影部分表示e-BAE有限振幅区域Figure 7. (a1)–(c1) The 2D poloidal mode structures of electrostatic potential
$ {\text{δ}} \phi $ for cases B, D and E in Fig. 5; (a2)–(c2) the radial profiles of dominant principal poloidal harmonic of$ {\text{δ}} {\phi }_{m=6} $ and corresponding phase angle$ {\theta }_{{\rm{r}}}= {\rm{a}}{\rm{r}}{\rm{c}}{\rm{t}}{\rm{a}}{\rm{n}}\dfrac{ {\rm{Im}} ({\text{δ}} {\phi }_{m=6}) } {{\rm{R}}{\rm{e}}({\text{δ}} {\phi }_{m=6} ) } $ , and the gray shaded region represents the radial domain with finite e-BAE amplitude.
图 8 (a)固定高能量电子在磁轴处的密度
$ {n}_{{\rm{h}}0, {\rm{a}}}/{n}_{{\rm{e}}0}= 0.05 $ , 向左和向右移动高能量电子密度剖面; (b)对应的密度梯度特征长度剖面Figure 8. (a) Fix the on-axis EE density with
$ {n}_{{\rm{h}}0, {\rm{a}}}/{n}_{{\rm{e}}0}= 0.05 $ and shift the density profile left and right; (b) the corresponding gradient scale length profiles.
图 9 (a1)—(c1)向左移动、未移动和向右移动高能量电子密度分布的e-BAE算例下静电势
$ {\text{δ}} \phi $ 的二维模结构; (a2)—(c2)主极向分量$ {\text{δ}} {\phi }_{m=6} $ 及其相位角$ {\theta }_{{\rm{r}}}={\rm{a}}{\rm{r}}{\rm{c}}{\rm{t}}{\rm{a}}{\rm{n}}\left({\rm{I}}{\rm{m}}\right({\text{δ}} {\phi }_{m=6})/{\rm{R}}{\rm{e}}({\text{δ}} {\phi }_{m=6}\left)\right) $ 的径向剖面.Figure 9. (a1)–(c1) The 2D poloidal mode structures of e-BAE electrostatic potential calculated using left-shifted, zero-shifted and right-shifted EE density profiles in Fig. 8; (a2)–(c2) the radial profiles of dominant principal poloidal harmonic of
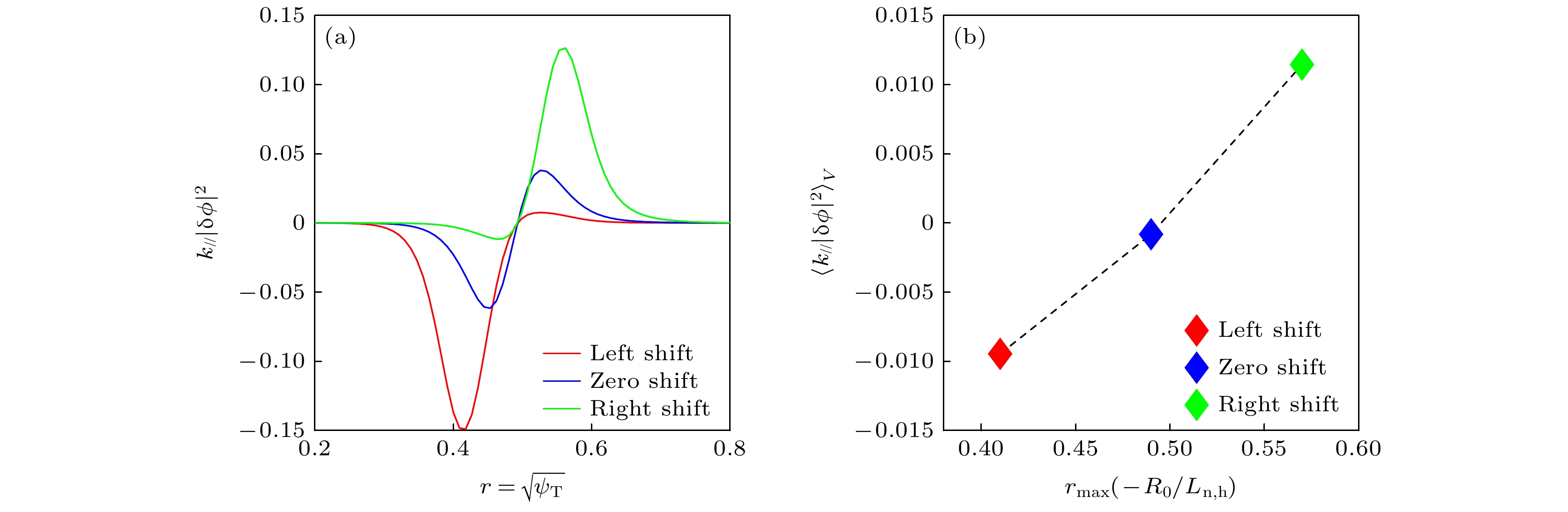
$ {\text{δ}} {\phi }_{m=6} $ and corresponding phase angle$ {\theta }_{{\rm{r}}}={\rm{a}}{\rm{r}}{\rm{c}}{\rm{t}}{\rm{a}}{\rm{n}}\left({\rm{I}}{\rm{m}}\right({\text{δ}} {\phi }_{m=6})/{\rm{R}}{\rm{e}}({\text{δ}} {\phi }_{m=6}\left)\right) $ .
图 10 (a)向左移动、未移动和向右移动高能量电子密度分布算例下
$ {k}_{/ /}{\left|{\text{δ}} \phi \right|}^{2} $ 的径向剖面; (b)对应的体积平均值$ {\langle{{k}_{/ /}{\left|{\text{δ}} \phi \right|}^{2}}\rangle}_{V} $ .Figure 10. (a) Radial profiles of
$ {k}_{/ /}{\left|{\text{δ}} \phi \right|}^{2} $ for cases using left-shifted, zero-shifted and right-shifted EE density distributions; (b) corresponding volume-averaged value of$ {\langle{{k}_{/ /}{\left|{\text{δ}} \phi \right|}^{2}}\rangle}_{V} $ . -
[1] Fasoli A, Gormenzano C, Berk H L, Breizman B, Briguglio S, Darrow D S, Gorelenkov N, Heidbrink W W, Jaun A, Konovalov S V, Nazikian R, Noterdaeme J M, Sharapov S, Shinohara K, Testa D, Tobita K, Todo T, Vlad G, Zonca F 2007 Nucl. Fusion 47 S264
Google Scholar
[2] Chen L, Zonca F, 2016 Rev. Mod. Phys. 88 015008
Google Scholar
[3] Heidbrink W W 2008 Phys. Plasmas 15 055501
Google Scholar
[4] Heidbrink W W 2020 Phys. Plasmas 27 030901
Google Scholar
[5] Chen W, Ding X T, Yang Q W, Liu Y, Ji X Q, Zhang Y P, Zhou J, Yuan G L, Sun H J, Li W, Zhou Y, Huang Y, Dong J Q, Feng B B, Song X M, Shi Z B, Liu Z T, Song X Y, Li L C, Duan X R, Liu Y 2010 Phys. Rev. Lett. 105 185004
Google Scholar
[6] Zhao N, Bao J, Chen W, Shi T H, Wang Z X, Yan N, Liu S C, Liu H Q, Zang Q, Lin S Y, Wu X H, Chu Y Q, Wang Y M, Wang S X, Hu W H, Chu N, Li M H, Zhai X M, Jie Y X, Jiang M, Lin X D, Gao X 2021 Nucl. Fusion 61 046013
Google Scholar
[7] Zonca F, Buratti P, Cardinali A, Chen L, Dong J Q, Long Y X, Milovanov A V, Romanelli F, Smeulders P, Wang L, Wang Z T, Castaldo C, Cesario R, Giovannozzi E, Marinucci M, Ridolfini V Pericoli 2007 Nucl. Fusion 47 1588
Google Scholar
[8] Ma R R, Qiu Z Y, Li Y Y, Chen W 2020 Nucl. Fusion 60 056019
Google Scholar
[9] Ma R R, Qiu Z Y, Li Y Y, Chen W 2021 Nucl. Fusion 61 036014
Google Scholar
[10] Cheng J Y, Zhang W L, Lin Z, Holod I, Li D, Chen Y, Cao J T 2016 Phys. Plasmas 23 052504
Google Scholar
[11] Wang J L, Todo Y, Wang H, Wang Z-X 2020 Nucl. Fusion 60 112012
Google Scholar
[12] Qiu Z Y, Chen L, Zonca F, Ma R R 2020 Plasma Phys. Control. Fusion 62 105012
Google Scholar
[13] Connor J, Hastie R J, Taylor J B 1979 Proc. Roy. Soc. London A 365 1720
[14] Lee W W, Lewandowski J L V, Hahm T S, Lin Z 2001 Phys. Plasmas 8 4435
Google Scholar
[15] Bao J, Zhang W L, Li D, Lin Z, Dong G, Liu C, Xie H S, Meng G, Cheng J Y, Dong C, Cao J T 2023 Nucl. Fusion 63 076021
Google Scholar
[16] Bao J, Zhang W L, Li D, Lin Z, Qiu Z Y, Chen W, Zhu X, Cheng J Y, Dong C, Cao J T 2023 Nucl. Fusion DOI: 10.1088/1741-4326/ad0598
[17] Bao J, Zhang W L, Li D, Lin Z 2020 J. Fusion Energ. 39 382
Google Scholar
[18] Zonca F, Chen L, Santoro R A 1996 Plasma Phys. Control. Fusion 38 2011
Google Scholar
[19] Wang X, Zonca F, Chen L 2010 Plasma Phys. Control. Fusion 52 115005
Google Scholar
[20] Ma R R, Zonca F, Chen L 2015 Phys. Plasmas 22 092501
Google Scholar
[21] Lu Z X, Wang X, Lauber Ph, Zonca F 2018 Nucl. Fusion 58 082021
Google Scholar
[22] Cheng C Z 1992 Phys. Rep. 211 1
Google Scholar
[23] Heidbrink W W, Hansen E C, Austin M E, Kramer G J, van Zeeland M A 2022 Nucl. Fusion 62 066020
Google Scholar
[24] Wang Z X, Lin Z, Holod I, Heidbrink W W, Tobias B, van Zeeland M, Austin M E 2013 Phys. Rev. Lett. 111 145003
Google Scholar
[25] Liu Y Q, Lin Z, Zhang H S, Zhang W L 2017 Nucl. Fusion 57 114001
Google Scholar
[26] Diamond P H, Kosuga Y, Gürcan Ö D, McDevitt C J, Hahm T S, Fedorczak N, Rice J E, Wang W X, Ku S, Kwon J M, Dif-Pradalier G, Abiteboul J, Wang L, Ko W H, Shi Y J, Ida K, Solomon W, Jhang H, Kim S S, Yi S, Ko S H, Sarazin Y, Singh R, Chang C S 2013 Nucl. Fusion 53 104019
Google Scholar
[27] Dong G, Wei X, Bao J, Brochard G, Lin Z, Tang W M 2021 Nucl. Fusion 61 126061
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 2372
- PDF Downloads: 71
- Cited By: 0
