-
In quantum key distribution (QKD), the users need to share the same reference frame. If their reference frames are inconsistent, the QKD system will not function properly. The most widely used method today is the active real-time calibration of both communication reference frames by using classical communication. In order to get rid of the real-time calibration operation of the reference frames, a QKD protocol independent of reference frame is proposed, called reference-frame-independent QKD (RFI-QKD). The RFI-QKD protocol is immune to the effects of slowly changing reference frame drift, requiring that only one set of bases should be aligned by Alice and Bob, and the remaining two sets of bases can slowly change in the channel. In the real QKD system, a set of basis vectors can always be found to maintain a stable alignment. However, some assumptions are made for the sources in most reported researches, i.e. with a trusted and fixed photon-number distribution (PND), which usually cannot be satisfied in practical implementations. Those unreasonable assumptions will inevitably compromise the security of practical QKD systems. To solve the problem, in this work, we present a passive light source monitoring (PLSM) scheme for RFI-QKD, which is accomplished by a passive monitoring module consisting of a beam splitter and two detectors on the source side. Through the PLSM module, we can have four monitoring events by using two local detectors and then precisely estimate the bounds of source distributions. Specifically, we take the three-intensity decoy-state-based RFI-QKD for example for illustraing the events. Compared with the original RFI-QKD, our PLSM method can passively monitor the PND and has many advantages, with light source fluctuations, finite-size effects and reference frame deflection angles taken into account.
-
Keywords:
- quantum key distribution /
- reference frame independent /
- passive light source monitoring /
- finite-size effect
[1] Charles H B, Gilles B 2014 Theor. Comput. Sci. 560 7
 Google Scholar
Google Scholar
[2] Ekert A K 1991 Phys. Rev. Lett. 67 661
 Google Scholar
Google Scholar
[3] Shor, Preskill 2000 Phys. Rev. Lett. 85 441
 Google Scholar
Google Scholar
[4] Dominic M 2001 J. ACM 48 351
 Google Scholar
Google Scholar
[5] Lo H K, Chau H F 1999 Science 283 2050
 Google Scholar
Google Scholar
[6] Charles H B, Francois B, Gilles B, Louis S, John S 1992 J. Cryptol. 5 3
 Google Scholar
Google Scholar
[7] Wang X B 2005 Phys. Rev. Lett. 94 230503
 Google Scholar
Google Scholar
[8] Jain N, Wittmann C, Lydersen L, Wiechers C, Elser D, Marquardt C, Makarov V, Leuchs G 2011 Phys. Rev. Lett. 107 110501
 Google Scholar
Google Scholar
[9] Dong Z Y, Yu N N, Wei Z J, Wang J D, Zhang Z M 2014 Eur. Phys. J. D 68 230
 Google Scholar
Google Scholar
[10] Anthony L, Valerio S, John G R, Jeremy L B 2010 Phys. Rev. A 82 012304
 Google Scholar
Google Scholar
[11] Tanumoy P, Byung K P, Cho Y W, Han S W, Kim Y S, Sung M 2017 Phys. Lett. A 381 2497
 Google Scholar
Google Scholar
[12] Zhang C M, Zhu J R, Wang Q 2018 J. Phys. Commun. 2 055029
 Google Scholar
Google Scholar
[13] Zhang C M, Zhu J R, Wang Q 2018 Eur. Phys. J. D 72 1
 Google Scholar
Google Scholar
[14] Zhu J R, Wang C Y, Liu K, Zhang C M, Wang Q 2018 Quantum Inf. Process. 17 1
 Google Scholar
Google Scholar
[15] Zhu J R, Zhang C M, Wang Q 2018 Phys. Lett. A 383 311
 Google Scholar
Google Scholar
[16] Zhang C M, Wang W B, Li H W, Wang Q 2019 Opt. Lett. 44 1226
 Google Scholar
Google Scholar
[17] Wang Q, Zhang C H, Wang X B 2016 Phys. Rev. A 93 032312
 Google Scholar
Google Scholar
[18] Zhang C H, Wang D, Zhou X Y, Wang S, Zhang L B, Yin Z Q, Chen W H, Z F, Guo G C, Wang Q 2018 Opt. Express 26 25921
 Google Scholar
Google Scholar
[19] Chi H H, Yu Z W, Wang X B 2012 Phys. Rev. A 86 042307
 Google Scholar
Google Scholar
[20] Jiang C, Yu Z W, Hu X L, Wang X B 2022 Natl. Sci. Rev. 10 4
[21] Wang X B, Peng C Z, Zhang J, Yang L, Pan J W 2008 Phys. Rev. A 77 042311
 Google Scholar
Google Scholar
[22] Xu F X, Zhang Y, Zhou Z, Chen W, Han Z F, Guo G C 2009 Phys. Rev. A 80 062309
 Google Scholar
Google Scholar
-
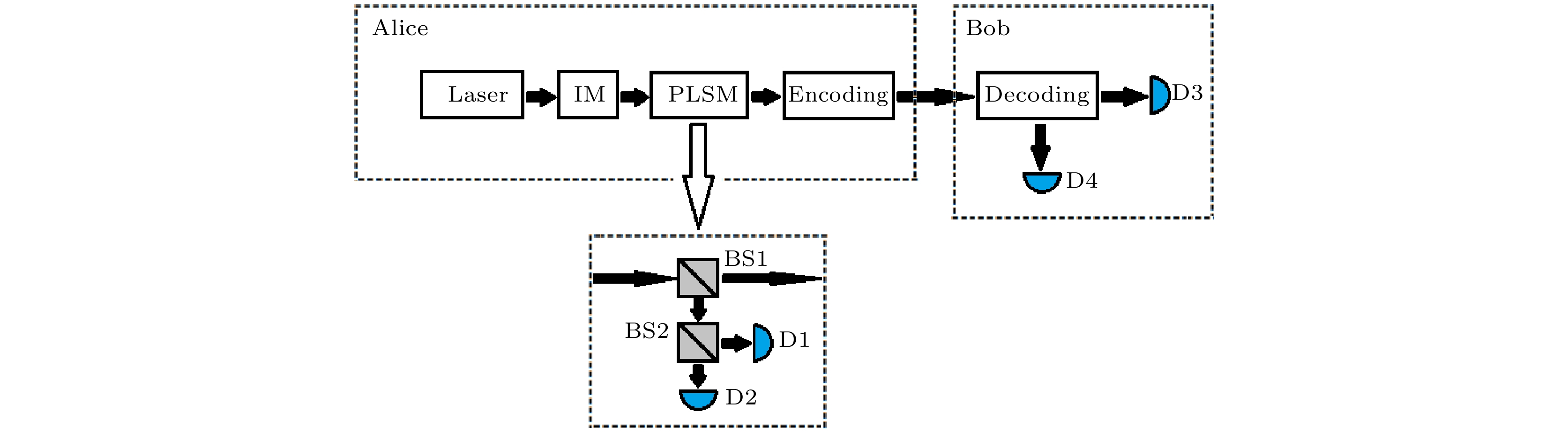
图 1 具有被动式光源监控功能的参考系无关量子密钥分发系统示意图. 被动式光源监控模块由光纤分束器和两个本地单光子探测器构成. IM表示强度调制器; Laser表示激光; BS表示分束器; D表示单光子探测器
Figure 1. Schematic of the RFI-QKD system with PLSM. The PLSM module is composed of beam splitters and two local single-photon detectors. The IM stands for the intensity modulator. The Laser stands for laser. BS stands for the beam splitter. D stands for the single-photon detector
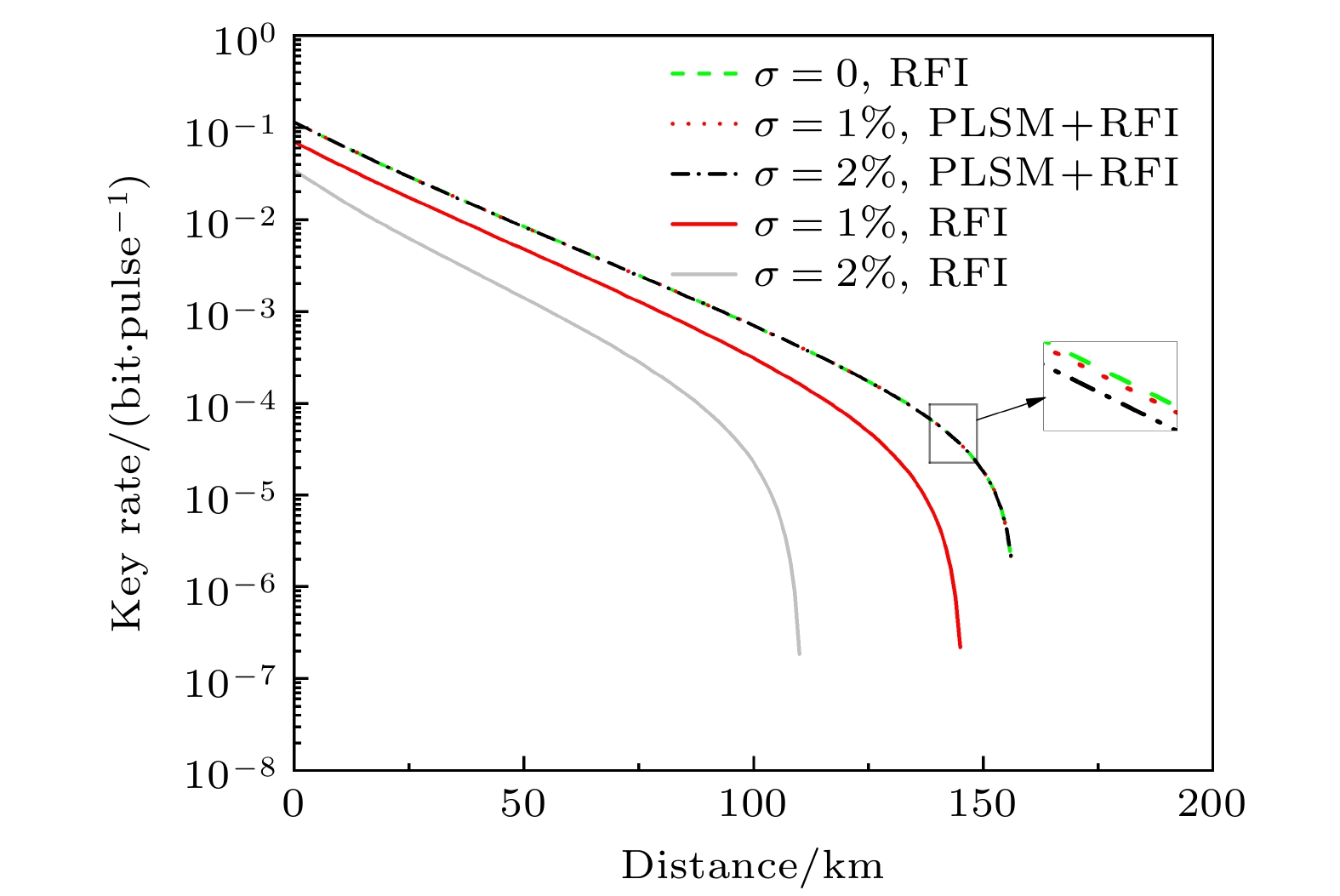
图 2 在固定偏转角和脉冲数, 起伏系数分别为
$ \sigma=0, $ $\sigma=1 $ %和$ \sigma= 2 $ %的条件下, 原始RFI-QKD和PLSM RFI-QKD的安全密钥率. 这里脉冲数$ N=10^{12} $ , 偏转角$ \beta=\pi/9 $ Figure 2. Key rate of different schemes with intensity fluctuation
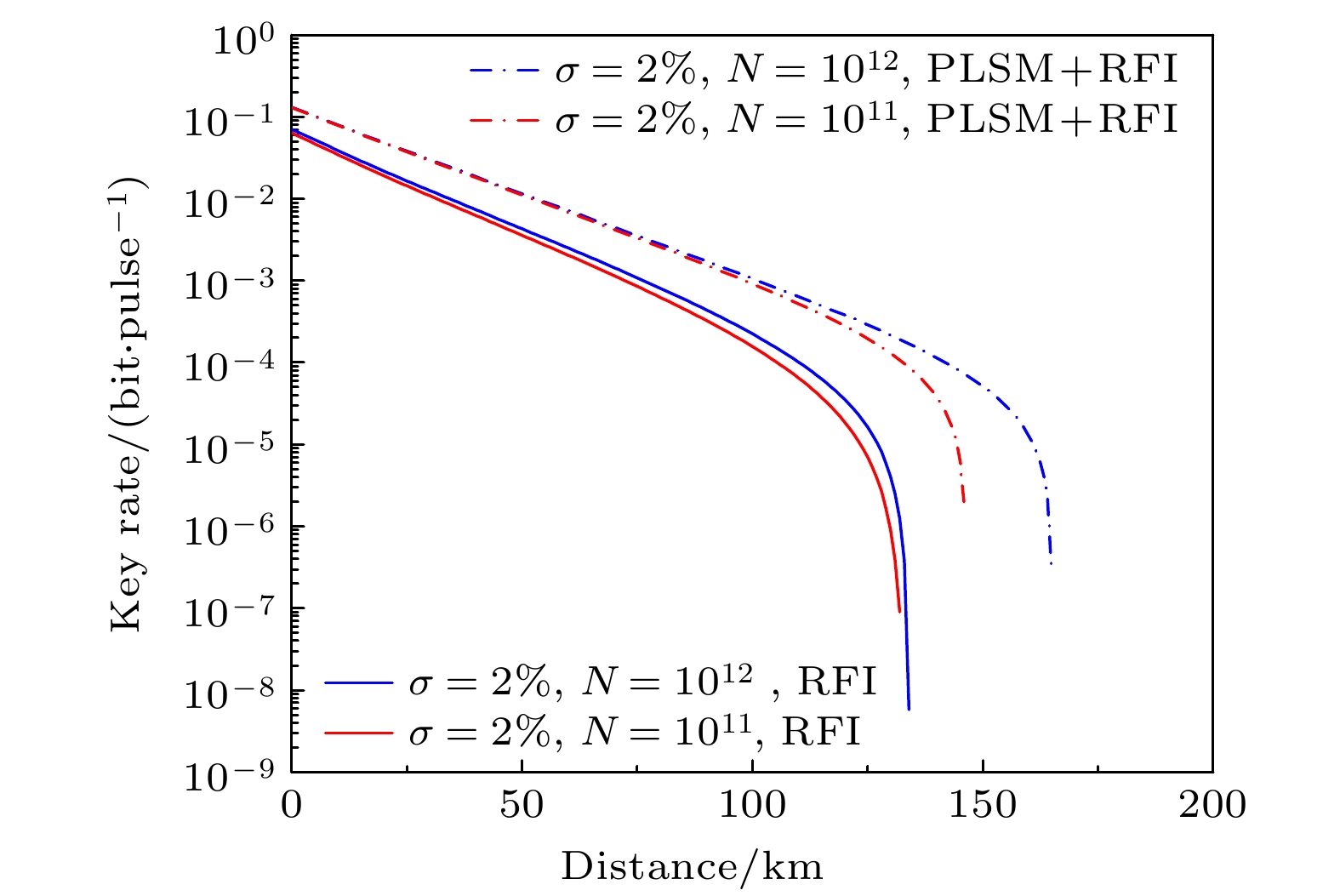
$ \sigma=0,\; \sigma=1 $ % and$ \sigma= 2 $ % under fixed deviation angle and with infinite number of pulses. Here the fixed deviation angle$ \beta=\pi/9 $ and the number of pulses$ N=10^{12} $ 图 3 在考虑光源起伏, 不同脉冲数的条件下, 原始RFI-QKD和PLSM RFI-QKD的安全密钥率. 这里偏转角
$ \beta=0 $ , 光源起伏系数$ \sigma=2 $ %Figure 3. Secret key rate of two schemes with different numbers of pulses when light source fluctuation is taken into account. Here the fixed deviation angle
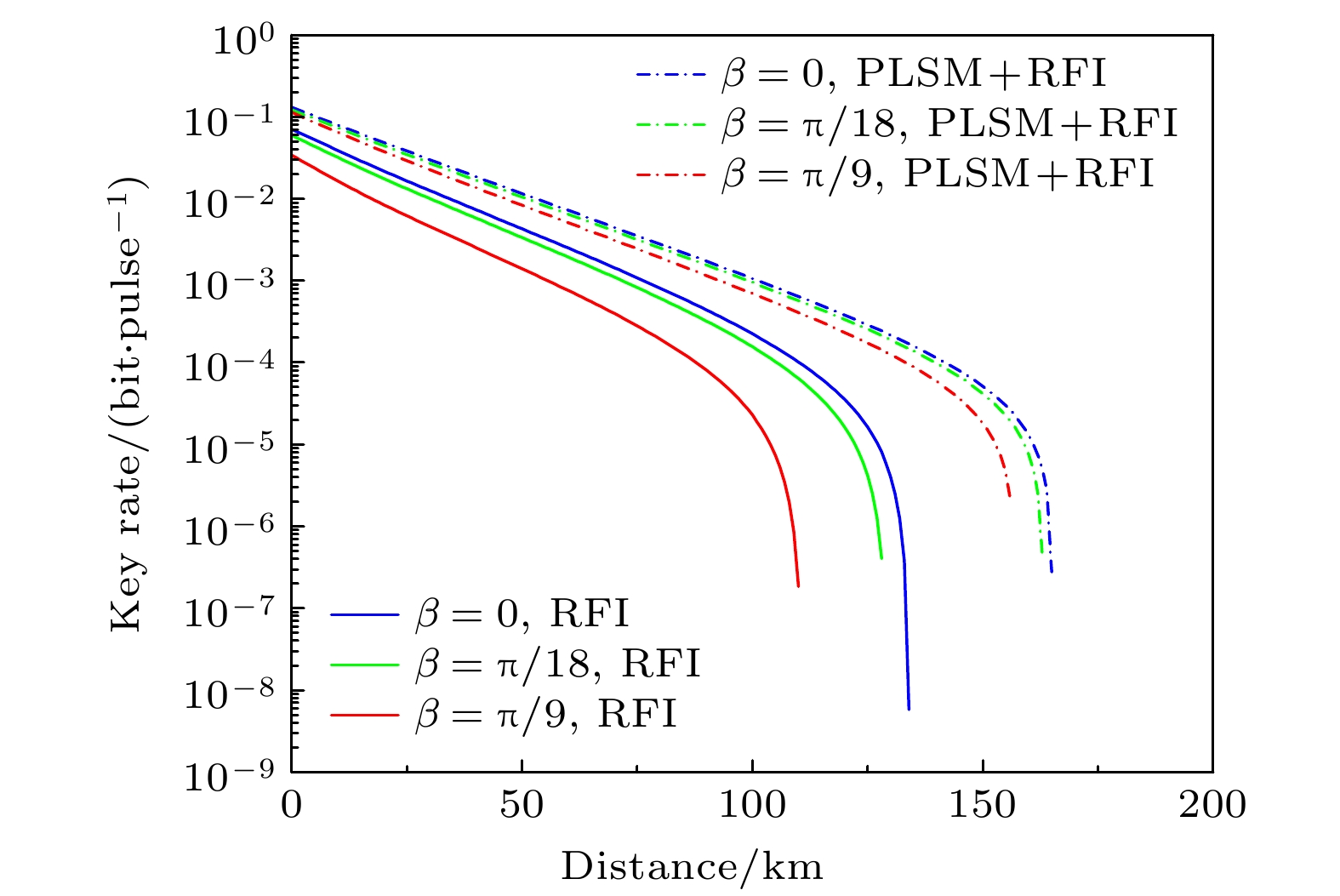
$ \beta=0 $ and fluctuation coefficient$ \sigma=2 $ %.图 4 在固定脉冲数和光源起伏系数, 不同偏转角的条件下, 原始RFI-QKD和PLSM-QKD的密钥率. 这里脉冲总数
$ N=10^{12} $ , 光源起伏系数$ \sigma=2 $ %Figure 4. Secret key rate of two schemes with different deviation angles of reference frame under fixed number of pulses and fluctuation coefficient. Here the number of pulses
$ N=10^{12} $ and source fluctuation coefficient$ \sigma=2 $ %.表 1 数值仿真中使用的基本系统参数
Table 1. Basic system parameters used in our numerical simulations.
$Y_0$ $e_{\rm{d}}$ α f γ $1\times 10^{-6}$ 0.015 0.2 dB/km 1.16 5.3 -
[1] Charles H B, Gilles B 2014 Theor. Comput. Sci. 560 7
 Google Scholar
Google Scholar
[2] Ekert A K 1991 Phys. Rev. Lett. 67 661
 Google Scholar
Google Scholar
[3] Shor, Preskill 2000 Phys. Rev. Lett. 85 441
 Google Scholar
Google Scholar
[4] Dominic M 2001 J. ACM 48 351
 Google Scholar
Google Scholar
[5] Lo H K, Chau H F 1999 Science 283 2050
 Google Scholar
Google Scholar
[6] Charles H B, Francois B, Gilles B, Louis S, John S 1992 J. Cryptol. 5 3
 Google Scholar
Google Scholar
[7] Wang X B 2005 Phys. Rev. Lett. 94 230503
 Google Scholar
Google Scholar
[8] Jain N, Wittmann C, Lydersen L, Wiechers C, Elser D, Marquardt C, Makarov V, Leuchs G 2011 Phys. Rev. Lett. 107 110501
 Google Scholar
Google Scholar
[9] Dong Z Y, Yu N N, Wei Z J, Wang J D, Zhang Z M 2014 Eur. Phys. J. D 68 230
 Google Scholar
Google Scholar
[10] Anthony L, Valerio S, John G R, Jeremy L B 2010 Phys. Rev. A 82 012304
 Google Scholar
Google Scholar
[11] Tanumoy P, Byung K P, Cho Y W, Han S W, Kim Y S, Sung M 2017 Phys. Lett. A 381 2497
 Google Scholar
Google Scholar
[12] Zhang C M, Zhu J R, Wang Q 2018 J. Phys. Commun. 2 055029
 Google Scholar
Google Scholar
[13] Zhang C M, Zhu J R, Wang Q 2018 Eur. Phys. J. D 72 1
 Google Scholar
Google Scholar
[14] Zhu J R, Wang C Y, Liu K, Zhang C M, Wang Q 2018 Quantum Inf. Process. 17 1
 Google Scholar
Google Scholar
[15] Zhu J R, Zhang C M, Wang Q 2018 Phys. Lett. A 383 311
 Google Scholar
Google Scholar
[16] Zhang C M, Wang W B, Li H W, Wang Q 2019 Opt. Lett. 44 1226
 Google Scholar
Google Scholar
[17] Wang Q, Zhang C H, Wang X B 2016 Phys. Rev. A 93 032312
 Google Scholar
Google Scholar
[18] Zhang C H, Wang D, Zhou X Y, Wang S, Zhang L B, Yin Z Q, Chen W H, Z F, Guo G C, Wang Q 2018 Opt. Express 26 25921
 Google Scholar
Google Scholar
[19] Chi H H, Yu Z W, Wang X B 2012 Phys. Rev. A 86 042307
 Google Scholar
Google Scholar
[20] Jiang C, Yu Z W, Hu X L, Wang X B 2022 Natl. Sci. Rev. 10 4
[21] Wang X B, Peng C Z, Zhang J, Yang L, Pan J W 2008 Phys. Rev. A 77 042311
 Google Scholar
Google Scholar
[22] Xu F X, Zhang Y, Zhou Z, Chen W, Han Z F, Guo G C 2009 Phys. Rev. A 80 062309
 Google Scholar
Google Scholar
Catalog
Metrics
- Abstract views: 5194
- PDF Downloads: 134
- Cited By: 0














 DownLoad:
DownLoad: