-
The phase change lattice Boltzmann (LB) model combined with the electric field model is employed to investigate the heat transfer performance of saturated pool boiling. Particular attention is paid to the influence of heater surface wettability and heater length on bubble behaviors, including generation, merging, and fracture during boiling in a uniform electric field. Moreover, the effects of the bubble behavior on heat transfer performance are also investigated. The study results indicate that the enhancement of boiling heat transfer by the electric field is dependent on both the heater length and the wettability. In the case of a hydrophilic surface, when the heater length
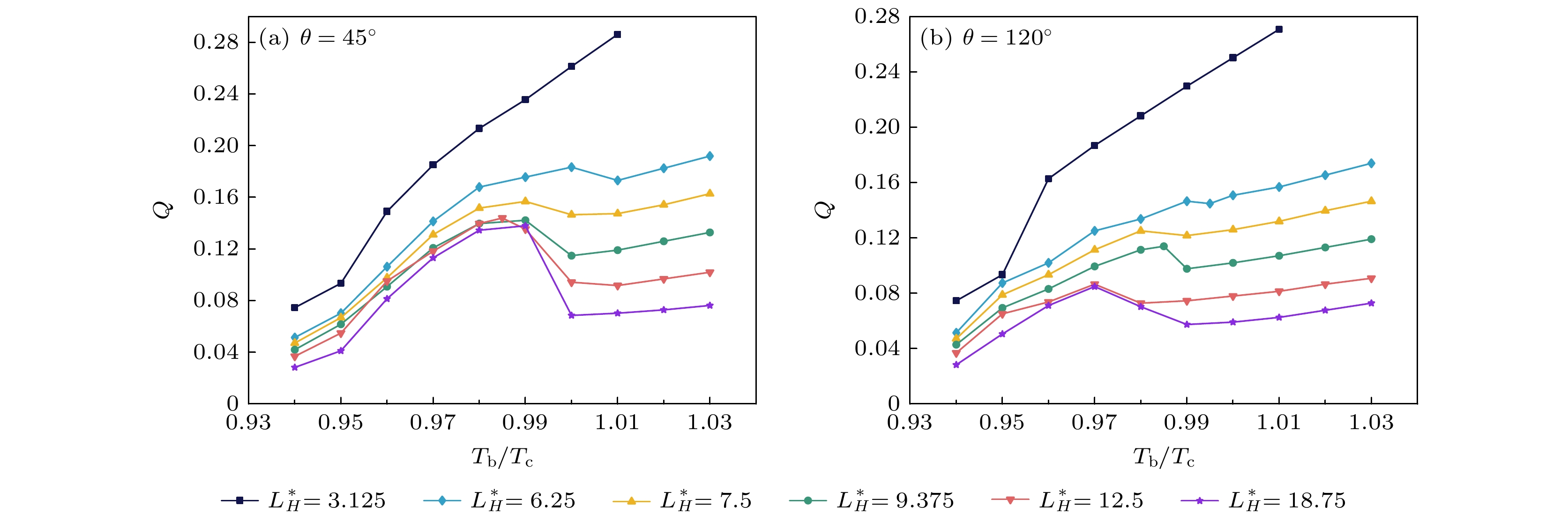
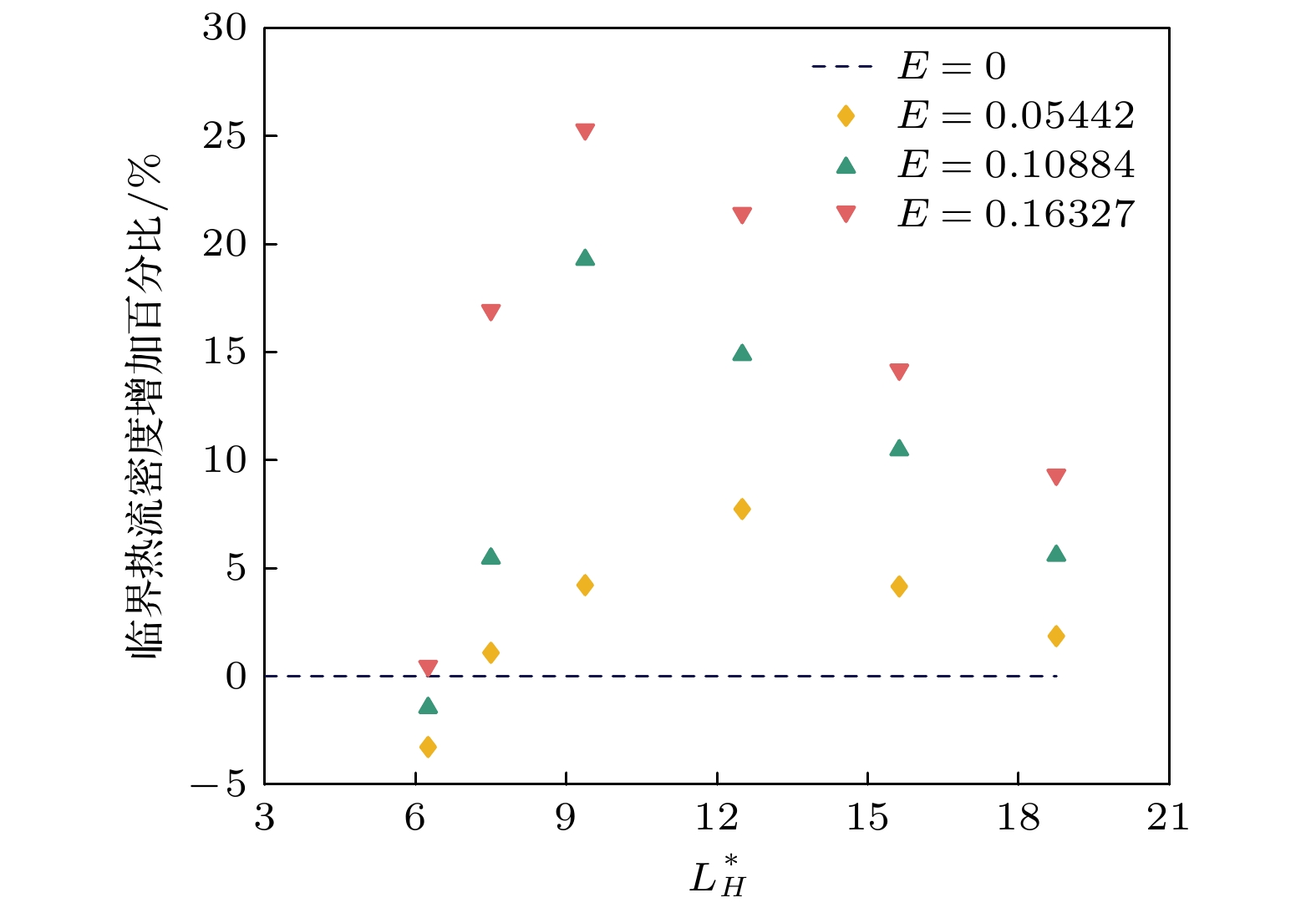
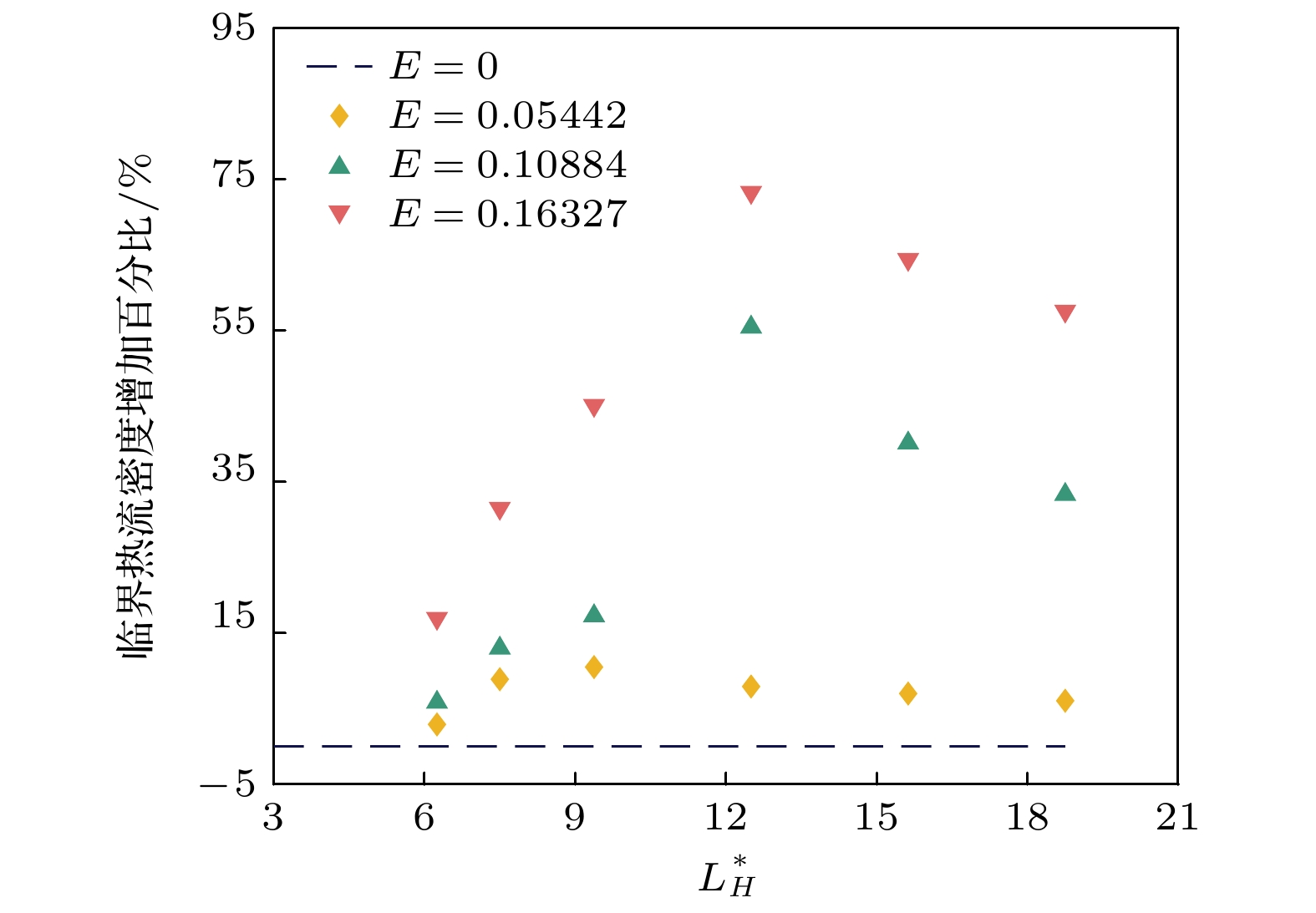
$L_H^*\leqslant 6.25$ , the bubble interaction force generated on the heater surface during boiling is weak due to the small size of the heater. Thus the effect of a uniform electric field on the bubble dynamic behaviors is mainly manifested by reducing the bubble size. As a result, the whole boiling phase is suppressed in this case. In the case of$6.25 < L_H^*\leqslant9.375$ , the uniform electric field enhances the critical heat flux (CHF), and the enhancement degree increases with electric field strength increasing. This can be attributed to the longer heater providing sufficient space for bubble generation, resulting in increased bubble nucleation sites and stronger interaction forces between bubbles. On the other hand, the distance between adjacent bubbles increases with the heater length increasing,thus further contributing to the improved CHF percentage. When$L_H^*>9.375$ , the rewetting resistance increases with heater length increasing. So the vapor generated in the boiling process is prone to be closely adhered to the heating surface under the action of electric field force, forming a thin layer of vapor on the heater surface. The vapor not only increases the heat transfer thermal resistance between the solid and the fluid but also creates no vortex near the bubble. This is not conducive to the movement of the bubble to the middle of the heater, thereby slowing down the heat mass exchange between the hot fluid on the heating surface and the colder fluid on both sides. As a result, the improved percentage of CHF decreases gradually with the increase in the heater length. In the case of hydrophobic surfaces, the increased percentage of CHF initially increases with heater length increasing and then decreases. However, comparing with the hydrophilic surface, the increase of the heater source length corresponds to the beginning of the decrease of critical heat flux.-
Keywords:
- uniform electric field /
- heater length /
- surface wettability /
- pool boiling
[1] 张海松, 徐进良, 朱鑫杰 2021 70 044401
Google Scholar
Zhang H S, Xu J L, Zhu X J 2021 Acta Phys. Sin. 70 044401
Google Scholar
[2] 曹春蕾, 何孝天, 马骁婧, 徐进良 2021 70 134703
Google Scholar
Cao C L, He X T, Ma X Q, Xu J L 2021 Acta Phys. Sin. 70 134703
Google Scholar
[3] 曾建邦, 李隆键, 廖全, 蒋方明 2011 60 066401
Google Scholar
Zeng J B, Li L J, Liao Q, Jiang F M 2011 Acta Phys. Sin. 60 066401
Google Scholar
[4] Gong S, Cheng P 2015 Int. J. Heat Mass Transfer 85 635
Google Scholar
[5] Lou A Q, Wang H, Li L 2023 Phys. Fluids 35 013316
Google Scholar
[6] 赵可, 佘阳梓, 蒋彦龙, 秦静, 张振豪 2019 68 244401
Google Scholar
Zhao K, She Y Z, Jiao Y L, Qin J, Zhang Z H 2019 Acta Phys. Sin. 68 244401
Google Scholar
[7] Clubb L 1916 UK Patent 100796 [1916-07-09
[8] Madadnia J, Koosha H 2003 Exp. Therm. Fluid Sci. 27 145
Google Scholar
[9] Gao M, Cheng P, Quan X J 2013 Int. J. Heat Mass Transfer 67 984
Google Scholar
[10] Dong W, Li R Y, Yu H L, Yan Y Y 2006 Exp. Therm. Fluid Sci. 30 579
Google Scholar
[11] Zu Y Q, Yan Y Y 2009 Int. J. Heat Mass Transfer 30 761
[12] Quan X J, Gao M, Cheng P, Li J S 2015 Int. J. Heat Mass Transfer 85 595
Google Scholar
[13] Liu B, Garivalis A I, Cao Z, Zhang Y, Wei J 2022 Int. J. Heat Mass Transfer 183 122154
Google Scholar
[14] Garivalis A I, Manfredini G, Saccone G, Di Marco P, Kossolapov A, Bucci M 2021 NPJ Microgravity 7 37
Google Scholar
[15] Nie L R, Yu L, Zheng Z, Shu C 2013 Phys. Rev. E 87 062142
Google Scholar
[16] Chen R Y, Pan W L, Zhang J Q, Nie L R 2016 Chaos 26 093113
Google Scholar
[17] Chen R Y, Tong L M, Nie L R, Wang C J, Pan W L 2017 Physica A 468 532
Google Scholar
[18] Du W, Kao J K, Shi Z, Nie L R 2023 Chin. Phys. B 32 020505
Google Scholar
[19] 李迎雪, 王浩原, 娄钦 2022 应用数学和力学 43 727
Google Scholar
Li Y X, Wang H Y, Lou Q 2022 Appl. Math. Mech. 43 727
Google Scholar
[20] Songoro H 2015 Ph.D. Dissertation (Darmstadt: Technische Universitat)
[21] Tomar G, Gerlach D, Biswas G, Alleborn N, Sharma A, Durst F, Welch S W J, Delgado A 2007 J. Comput. Phys. 227 1267
Google Scholar
[22] Pandey V, Biswas G, Dalal A 2016 Phys. Fluids 28 052102
Google Scholar
[23] Shan X, Chen H 1993 Phys. Rev. E 47 1815
Google Scholar
[24] Gong S, Cheng P 2017 Int. Commun. Heat Mass Transfer 87 61
Google Scholar
[25] Ma X, Cheng P, Gong S, Quan X 2017 Int. J. Heat Mass Transfer 114 453
Google Scholar
[26] Feng Y, Li H, Guo K, Lei X, Zhao J 2019 Int. J. Heat Mass Transfer 135 885
Google Scholar
[27] 张浏斌, 单彦广, 戎志成 2022 计算物理 39 12
Zhang L B, Shan Y G, Rong Z C 2022 Chin. J. Comput. Phys. 39 12
[28] Yao J D, Luo K, Wu J, Yi H L 2022 Phys. Fluids 34 013606
Google Scholar
[29] Li W X, Li Q, Chang H Z, Yu Y, Tang S 2022 Phys. Fluids 34 123327
Google Scholar
[30] Rainey K N, You S M 2001 Int. J. Heat Mass Transfer 44 2589
Google Scholar
[31] Lee S Y, Tong K K, Park C M, Kim M H, Jo H J 2022 Appl. Therm. Eng. 2 213
[32] Zhang C, Cheng P, Hong F 2016 Int. J. Heat Mass Transfer 101 1331
Google Scholar
[33] Wang H Y, Lou Q, Liu G J, Li L 2022 Int. J. Therm. Sci. 178 107554
Google Scholar
[34] Gong S, Cheng P 2012 Int. J. Heat Mass Transfer 55 4923
Google Scholar
[35] Qian Y H, D'Humières1 D, Lallemand P 1992 EPL 17 479
Google Scholar
[36] Guo Z L, Shi B C, Wang N C 2000 J. Comput Phys. 165 288
Google Scholar
[37] Panofsky W, Phillips M, Jauch J M 1956 AM. J. Phys. 24 416
[38] He X, Ning L 2000 Comput. Phys. Commun. 129 158
Google Scholar
[39] Ding H, Spelt P 2007 Phys. Rev. E 75 046708
Google Scholar
[40] Li L, Chen C, Mei R, Mei M, Klausner J 2014 Phys. Rev. E 89 043308
Google Scholar
-
图 1 物理问题示意图
Figure 1. Diagram of the physical problem.
图 2 (a)亲水表面和(b)疏水表面不同长度加热器的沸腾曲线
Figure 2. Boiling curves of heaters with different lengths: (a) Hydrophilic surfaces; (b) hydrophobic surfaces.
图 3
$L_H^* = 3.125$ ,$t^* = 66.99$ 时刻, 不同加热温度下的气泡形态 (a)$T_\mathrm{b} = 0.98 T_\mathrm{c}$ ; (b)$T_\mathrm{b} = 1.00 T_\mathrm{c}$ ; (c)$T_\mathrm{b} = 1.02 T_\mathrm{c}$ Figure 3. The bubble morphology at
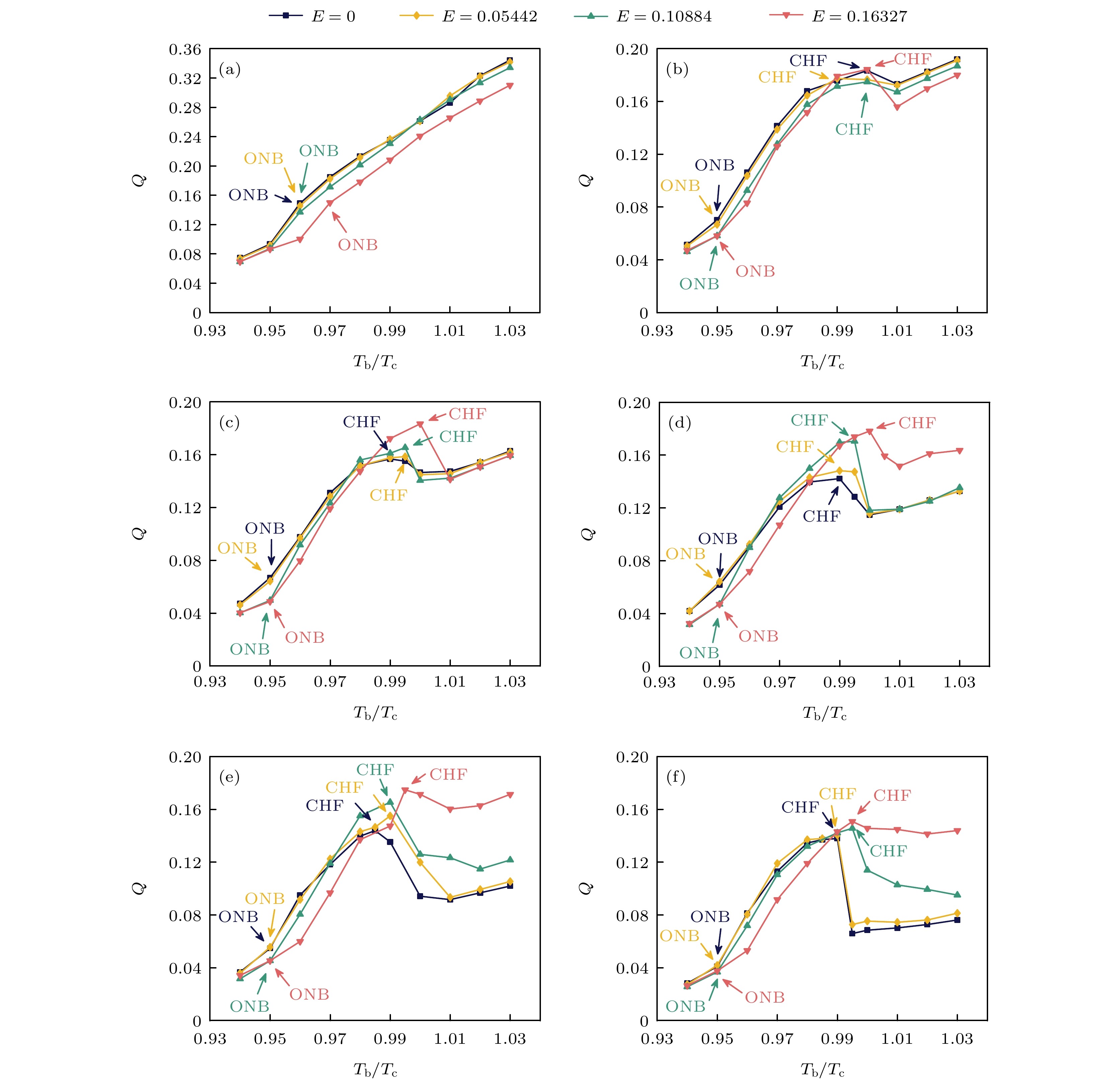
$L_H^*=3.125$ ,$t^*=66.99$ moments with different heating temperatures: (a)$T_\mathrm{b}= $ $ 0.98 T_\mathrm{c}$ ; (b)$T_\mathrm{b}=1.00 T_\mathrm{c}$ ; (c)$T_\mathrm{b}=1.02 T_\mathrm{c}$ .
图 4
$t^*=55.83, T_\mathrm{b}=0.98 T_\mathrm{c}$ 条件下, 不同长度加热器下沸腾的气泡形态和流场 (a)$L_H^*=6.25$ ; (b)$L_H^*=18.75$ Figure 4. Bubble morphology and flow field for boiling with different length heaters under
$t^*=55.83, T_\mathrm{b}=0.98 T_\mathrm{c}$ conditions: (a)$L_H^*=6.25$ ; (b)$L_H^*=18.75$ .
图 5 亲水表面不同长度加热器在不同电场强度下的沸腾曲线 (a)
$L_H^*=3.125$ ; (b)$L_H^*=6.25$ ; (c)$L_H^*=7.5$ ; (d)$L_H^*= $ $ 9.375$ ; (e)$L_H^*=12.5$ ; (f)$L_H^*=18.75$ Figure 5. Boiling curves of heaters of different lengths on hydrophilic surfaces under different electric field strengths: (a)
$L_H^*=3.125$ ; (b)$L_H^*=6.25$ ; (c)$L_H^*=7.5$ ; (d)$L_H^*=9.375$ ; (e)$L_H^*=12.5$ ; (f)$L_H^*=18.75$ .
图 6
$L_H^*=6.25$ 时, 在均匀电场强度$E=0, 0.16327$ 作用下 (a)$T_\mathrm{b}=0.97 T_\mathrm{c}$ , 核态沸腾状态; (b)$T_\mathrm{b}=1.02 T_\mathrm{c}$ , 膜态沸腾状态的气泡形态Figure 6. The bubble morphology of (a)
$T_\mathrm{b}=0.97 T_\mathrm{c}$ , nucleated boiling state; (b)$T_\mathrm{b}=1.02 T_\mathrm{c}$ , film boiling state under the action of uniform electric field strength$E=0, 0.16327$ ,$L_H^*=6.25$ .
图 7 不同长度加热器在电场强度
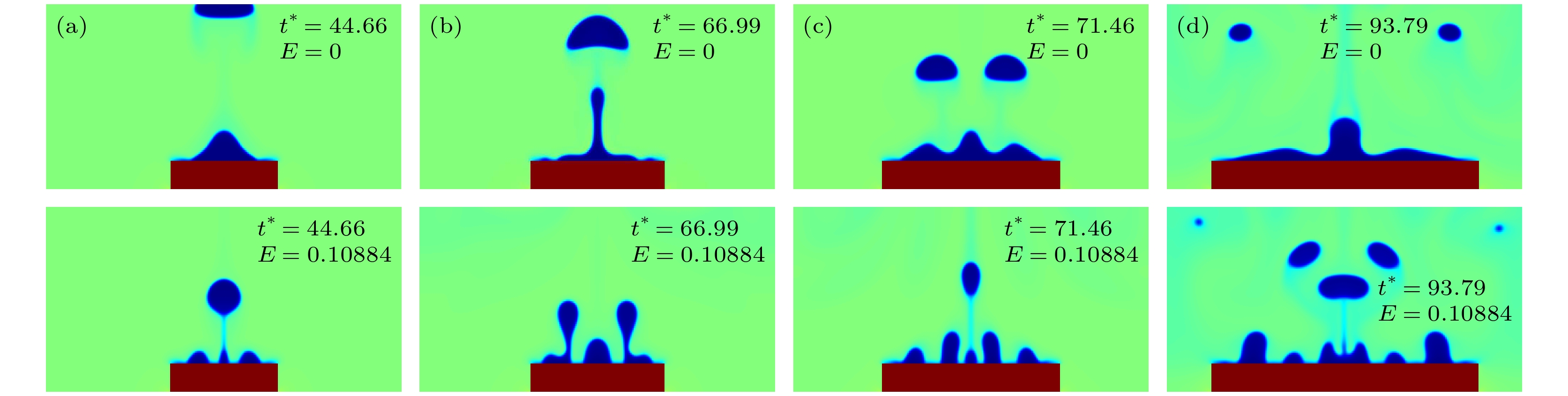
$E=0, 0.10884$ 下的气泡形态对比 (a)$L_H^*=7.5$ ; (b)$L_H^*=9.375$ ; (c)$L_H^*=12.5$ ; (d)$L_H^*=18.75$ Figure 7. Comparison of bubble morphology of heaters with different lengths at electric field strength
$E=0, 0.10884$ : (a)$L_H^*=7.5$ ; (b)$L_H^*=9.375$ ; (c)$L_H^*=12.5$ ; (d)$L_H^*=18.75$ .
图 8 不同电场强度下亲水表面加热器长度与临界热流密度的关系
Figure 8. Relationship between hydrophilic surface heater length and critical heat flow density at different electric field strengths.
图 9 均匀电场强度
$E=0.10884$ 作用下,$T_\mathrm{b}=0.995 T_\mathrm{c}$ 沸腾过程的空间平均热流密度随时间的变化Figure 9. Spatially averaged heat flow density with time for
$T_\mathrm{b}=0.995 T_\mathrm{c}$ boiling process under uniform electric field strength$E=0.10884$ .
图 10 均匀电场强度
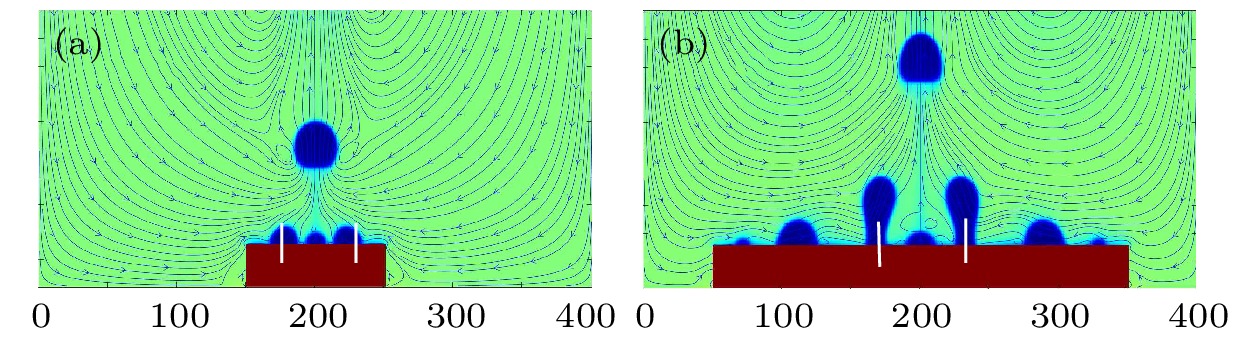
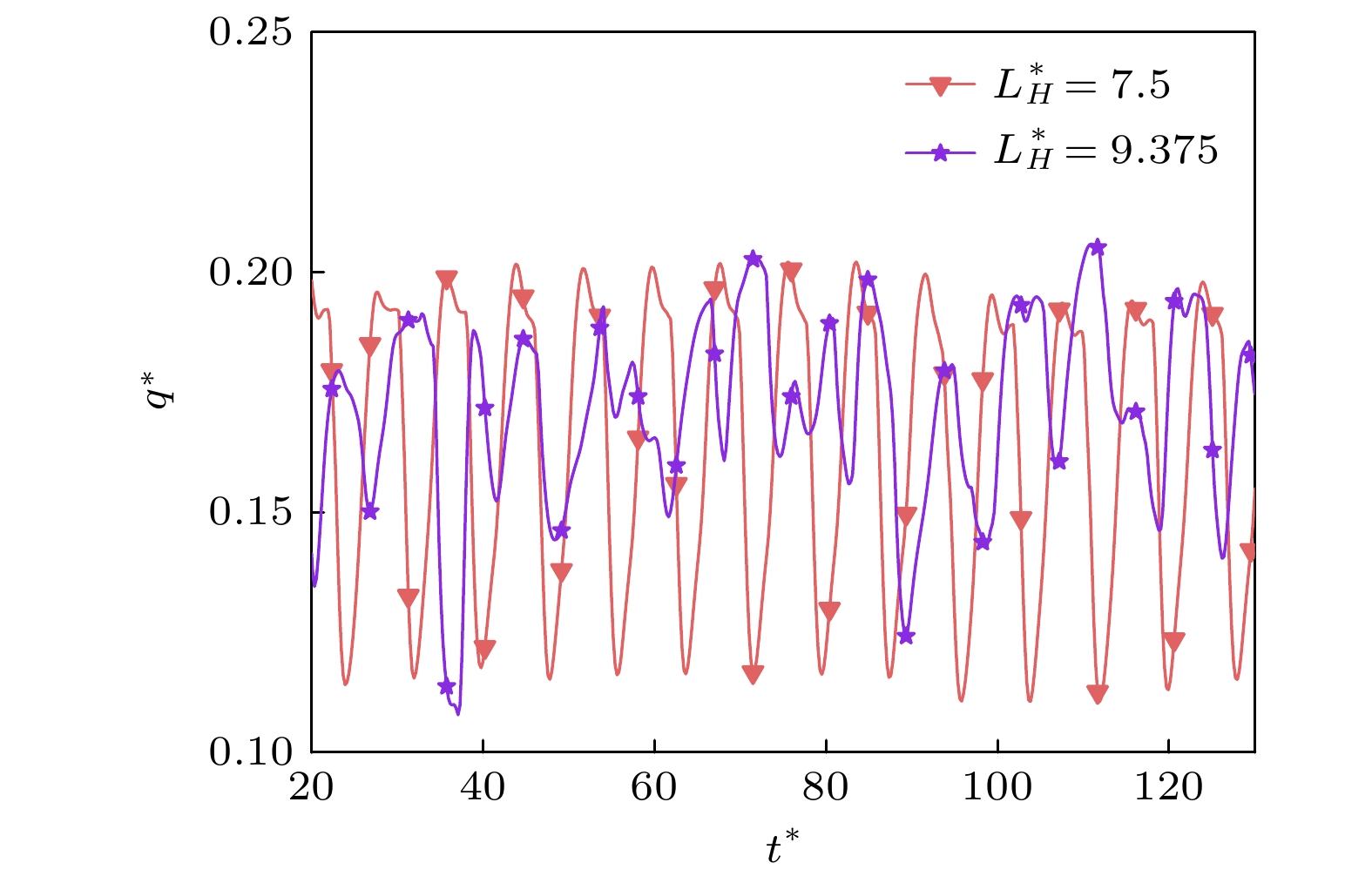
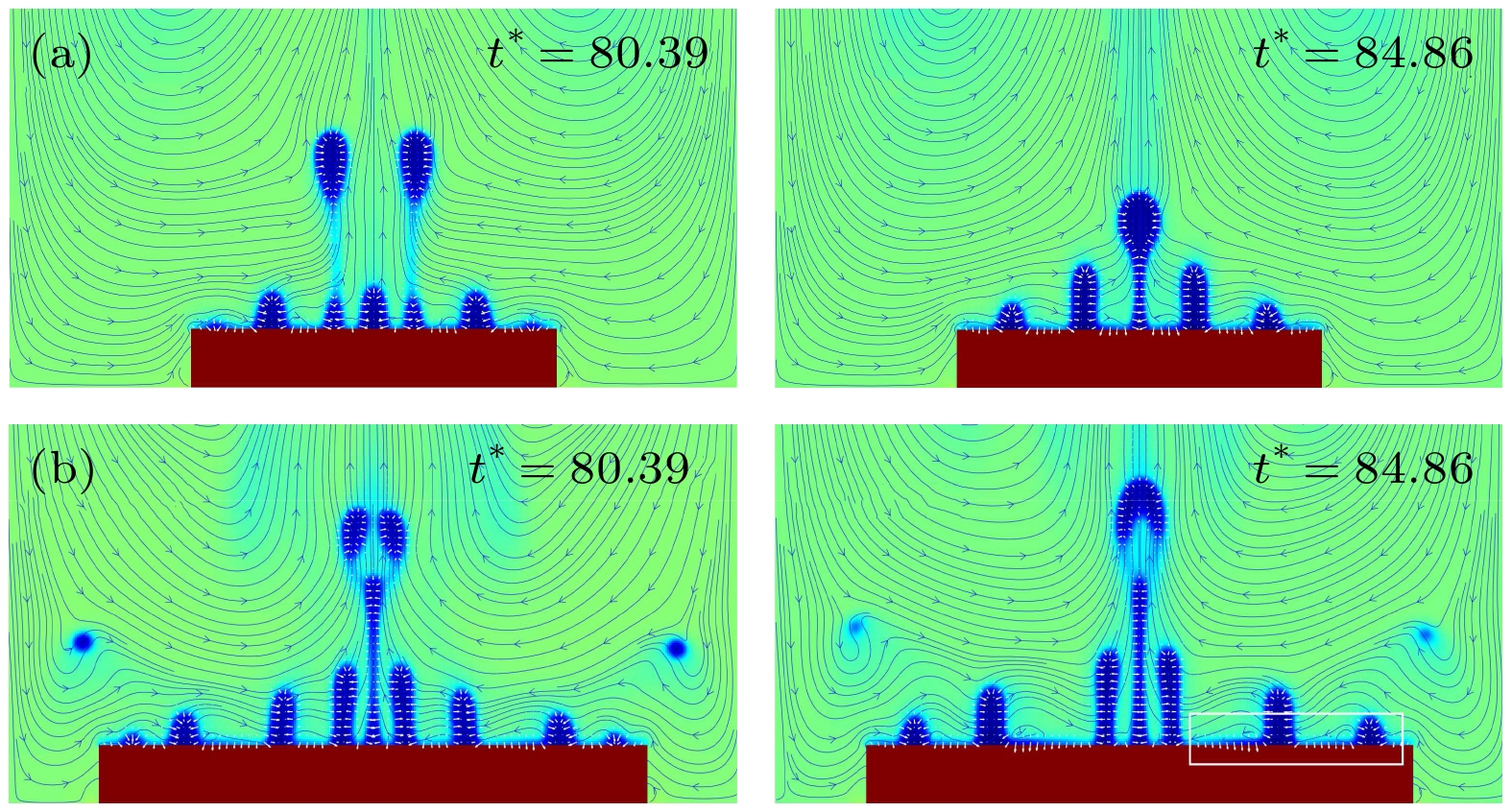
$E=0.10884$ 作用下,$T_\mathrm{b}=0.995 T_\mathrm{c}$ 沸腾状态的气泡形态演变、当前时刻气泡所受电场力和当前时刻流场分布 (a)$L_H^*=7.5$ ; (b)$L_H^*=9.375$ Figure 10. Evolution of bubble morphology, electric field force on the bubble at the current moment and flow field distribution at the current moment under the action of uniform electric field strength
$E=0.10884$ ,$T_\mathrm{b}=0.995 T_\mathrm{c}$ boiling state: (a)$L_H^*=7.5$ ; (b)$L_H^*=9.375$ .
图 11 均匀电场强度
$E=0.16327$ 作用下,$T_\mathrm{b}=0.995 T_\mathrm{c}$ 沸腾过程的空间平均热流密度随时间的变化Figure 11. Spatially averaged heat flow density with time for
$T_\mathrm{b}=0.995 T_\mathrm{c}$ boiling process under uniform electric field strength$E=0.16327$ .
图 12 均匀电场强度
$E=0.16327$ 作用下,$T_\mathrm{b}=0.995 T_\mathrm{c}$ 沸腾状态的气泡形态演变、当前时刻气泡所受电场力和当前时刻流场分布 (a)$L_H^*=12.5$ ; (b)$L_H^*=18.75$ Figure 12. Evolution of bubble morphology, electric field force on the bubble at the current moment and flow field distribution at the current moment under the action of uniform electric field strength
$E=0.16327$ ,$T_\mathrm{b}=0.995 T_\mathrm{c}$ boiling state: (a)$L_H^*=12.5$ ; (b)$L_H^*=18.75$ .
图 13 疏水表面不同长度加热器在不同电场强度下的沸腾曲线 (a)
$L_H^*=3.125$ ; (b)$L_H^*=6.25$ ; (c)$L_H^*=7.5$ ; (d)$L_H^*= $ $ 9.375$ ; (e)$L_H^*=12.5$ ; (f)$L_H^*=18.75$ Figure 13. Boiling curves of different lengths of heaters on hydrophobic surfaces under different electric field strengths: (a)
$L_H^*= 3.125$ ; (b)$L_H^*=6.25$ ; (c)$L_H^*=7.5$ ; (d)$L_H^*=9.375$ ; (e)$L_H^*=12.5$ , (f)$L_H^*=18.75$ .
图 14
$t_0^*=80.39$ 时刻,$T_\mathrm{b}=0.99 T_\mathrm{c}$ 时 (a)$E=0$ ; (b)$E= $ $ 0.16327$ 的疏水表面对应的气泡动力学行为Figure 14. The bubble dynamics behavior of the hydrophobic surface: (a)
$E=0$ , (b)$E=0.16327$ at the$t_0^*=80.39$ ,$T_\mathrm{b}=0.99 T_\mathrm{c}$ .
图 15 不同电场强度下疏水表面加热器长度与临界热流密度(CHF)的关系
Figure 15. Relationship between hydrophobic surface heater length and critical heat flow density (CHF) at different electric field strengths.
表 1 格子单位与物理单位转换
Table 1. The unit conversion from lattice unit to physical unit.
符号 格子单
位大小物理单位大小 转换因子 $ \rho_\mathrm{l} $ 5.426 570.02 $ \mathrm{kg}/\mathrm{m}^3 $ 106.16 $ \mathrm{kg}/\mathrm{m}^3 $ $ \rho_\mathrm{v} $ 0.8113 86.13 $ \mathrm{kg}/\mathrm{m}^3 $ 106.16 $ \mathrm{kg}/\mathrm{m}^3 $ $ l_0 $ 16 $ 4.72\times 10^{-6}\;\mathrm{m} $ $ 2.95\times 10^{-7}\;\mathrm{m} $ $ u_0 $ 0.0358 38.56 $ \mathrm{m/s} $ 1077.09 $ \mathrm{m/s} $ $ t_0 $ 447.8 $ 1.224\times 10^{-7}\;\mathrm{s} $ $ 2.734\times 10^{-10}\;\mathrm{s} $ ν 0.06 $ 0.19\times 10^{-4}\;\mathrm{m}^2/\mathrm{s} $ $ 3.18\times 10^{-4}\;\mathrm{m}^2/\mathrm{s} $ $ T_\mathrm{c} $ 0.1961 647.2 $ \mathrm{K} $ 3300.36 $ \mathrm{K} $ $ p_\mathrm{c} $ 0.1784 $ 0.221\times 10^{8}\;\mathrm{Pa} $ $ 1.24\times 10^{8}\;\mathrm{Pa} $ $ c_\mathrm{vl} $ 4.0 1405.9 $\mathrm{J}/(\mathrm{kg}{\cdot} \mathrm{K})$ 351.48 $ \mathrm{J}/(\mathrm{kg}\cdot \mathrm{K}) $ $ h_\mathrm{fg} $ 0.624 $ 0.726\times 10^{6}\;\mathrm{J/kg} $ $ 1.16\times 10^{6}\;\mathrm{J/kg} $ $ \lambda_\mathrm{s} $ 32.556 390.67 $\mathrm{W}/(\mathrm{m}{\cdot} \mathrm{K})$ 12.0 $ \mathrm{W}/(\mathrm{m}\cdot \mathrm{K}) $ $ q_0 $ 0.01269 $1.69 \times 10^{9}\;\mathrm{J}/({\rm{m} }^2{\cdot} {\rm{s} })$ $1.33 \times 10^{11}\;\mathrm{J}/({\rm{m} }^2{\cdot} {\rm{s} })$ $ \varepsilon_0\varepsilon_\mathrm{l} $ 2.236 $ 1.98\times 10^{-11}\;\mathrm{F/m} $ $ 8.85\times 10^{-12}\;\mathrm{F/m} $ $ \varepsilon_0\varepsilon_\mathrm{v} $ 1 $ 8.85\times 10^{-12}\;\mathrm{F/m} $ $ 8.85\times 10^{-12}\;\mathrm{F/m} $ V 1 1096.96 V 1096.96 V 
DownLoad: CSV
-
[1] 张海松, 徐进良, 朱鑫杰 2021 70 044401
Google Scholar
Zhang H S, Xu J L, Zhu X J 2021 Acta Phys. Sin. 70 044401
Google Scholar
[2] 曹春蕾, 何孝天, 马骁婧, 徐进良 2021 70 134703
Google Scholar
Cao C L, He X T, Ma X Q, Xu J L 2021 Acta Phys. Sin. 70 134703
Google Scholar
[3] 曾建邦, 李隆键, 廖全, 蒋方明 2011 60 066401
Google Scholar
Zeng J B, Li L J, Liao Q, Jiang F M 2011 Acta Phys. Sin. 60 066401
Google Scholar
[4] Gong S, Cheng P 2015 Int. J. Heat Mass Transfer 85 635
Google Scholar
[5] Lou A Q, Wang H, Li L 2023 Phys. Fluids 35 013316
Google Scholar
[6] 赵可, 佘阳梓, 蒋彦龙, 秦静, 张振豪 2019 68 244401
Google Scholar
Zhao K, She Y Z, Jiao Y L, Qin J, Zhang Z H 2019 Acta Phys. Sin. 68 244401
Google Scholar
[7] Clubb L 1916 UK Patent 100796 [1916-07-09
[8] Madadnia J, Koosha H 2003 Exp. Therm. Fluid Sci. 27 145
Google Scholar
[9] Gao M, Cheng P, Quan X J 2013 Int. J. Heat Mass Transfer 67 984
Google Scholar
[10] Dong W, Li R Y, Yu H L, Yan Y Y 2006 Exp. Therm. Fluid Sci. 30 579
Google Scholar
[11] Zu Y Q, Yan Y Y 2009 Int. J. Heat Mass Transfer 30 761
[12] Quan X J, Gao M, Cheng P, Li J S 2015 Int. J. Heat Mass Transfer 85 595
Google Scholar
[13] Liu B, Garivalis A I, Cao Z, Zhang Y, Wei J 2022 Int. J. Heat Mass Transfer 183 122154
Google Scholar
[14] Garivalis A I, Manfredini G, Saccone G, Di Marco P, Kossolapov A, Bucci M 2021 NPJ Microgravity 7 37
Google Scholar
[15] Nie L R, Yu L, Zheng Z, Shu C 2013 Phys. Rev. E 87 062142
Google Scholar
[16] Chen R Y, Pan W L, Zhang J Q, Nie L R 2016 Chaos 26 093113
Google Scholar
[17] Chen R Y, Tong L M, Nie L R, Wang C J, Pan W L 2017 Physica A 468 532
Google Scholar
[18] Du W, Kao J K, Shi Z, Nie L R 2023 Chin. Phys. B 32 020505
Google Scholar
[19] 李迎雪, 王浩原, 娄钦 2022 应用数学和力学 43 727
Google Scholar
Li Y X, Wang H Y, Lou Q 2022 Appl. Math. Mech. 43 727
Google Scholar
[20] Songoro H 2015 Ph.D. Dissertation (Darmstadt: Technische Universitat)
[21] Tomar G, Gerlach D, Biswas G, Alleborn N, Sharma A, Durst F, Welch S W J, Delgado A 2007 J. Comput. Phys. 227 1267
Google Scholar
[22] Pandey V, Biswas G, Dalal A 2016 Phys. Fluids 28 052102
Google Scholar
[23] Shan X, Chen H 1993 Phys. Rev. E 47 1815
Google Scholar
[24] Gong S, Cheng P 2017 Int. Commun. Heat Mass Transfer 87 61
Google Scholar
[25] Ma X, Cheng P, Gong S, Quan X 2017 Int. J. Heat Mass Transfer 114 453
Google Scholar
[26] Feng Y, Li H, Guo K, Lei X, Zhao J 2019 Int. J. Heat Mass Transfer 135 885
Google Scholar
[27] 张浏斌, 单彦广, 戎志成 2022 计算物理 39 12
Zhang L B, Shan Y G, Rong Z C 2022 Chin. J. Comput. Phys. 39 12
[28] Yao J D, Luo K, Wu J, Yi H L 2022 Phys. Fluids 34 013606
Google Scholar
[29] Li W X, Li Q, Chang H Z, Yu Y, Tang S 2022 Phys. Fluids 34 123327
Google Scholar
[30] Rainey K N, You S M 2001 Int. J. Heat Mass Transfer 44 2589
Google Scholar
[31] Lee S Y, Tong K K, Park C M, Kim M H, Jo H J 2022 Appl. Therm. Eng. 2 213
[32] Zhang C, Cheng P, Hong F 2016 Int. J. Heat Mass Transfer 101 1331
Google Scholar
[33] Wang H Y, Lou Q, Liu G J, Li L 2022 Int. J. Therm. Sci. 178 107554
Google Scholar
[34] Gong S, Cheng P 2012 Int. J. Heat Mass Transfer 55 4923
Google Scholar
[35] Qian Y H, D'Humières1 D, Lallemand P 1992 EPL 17 479
Google Scholar
[36] Guo Z L, Shi B C, Wang N C 2000 J. Comput Phys. 165 288
Google Scholar
[37] Panofsky W, Phillips M, Jauch J M 1956 AM. J. Phys. 24 416
[38] He X, Ning L 2000 Comput. Phys. Commun. 129 158
Google Scholar
[39] Ding H, Spelt P 2007 Phys. Rev. E 75 046708
Google Scholar
[40] Li L, Chen C, Mei R, Mei M, Klausner J 2014 Phys. Rev. E 89 043308
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 2876
- PDF Downloads: 89
- Cited By: 0
