-
微尺度系统传热具有较小的热惯性和较快的热响应, 在控制传热方面具有独到的优势. 本文利用分子动力学方法研究了纳米通道中壁面温度及壁面润湿性不同时, 静态流体和动态流体下界面热阻的变化规律. 结果表明, 在静态流体中, 壁面润湿性的增强会显著降低界面热阻, 对于温度不同的壁面, 当润湿性较弱时, 可以观察到高温壁面处的界面热阻高于低温壁面处, 反之, 当润湿性较强时, 壁面温度对界面热阻的影响较小; 对流体区域施加外力使流体流动, 结果显示外力的增加能有效提高系统的热通量, 流体温度升高. 当润湿性较弱时, 外力的增大能显著减低界面热阻, 而随着壁面润湿性增强, 外力对界面热阻的影响逐渐减小. 此外, 本文将界面热阻与壁面吸附流体分子数量相联系, 发现在静态流体中, 界面热阻值与壁面吸附流体分子的数量呈负相关; 而在动态流体中, 外力的变化对吸附分子数量的影响较小, 壁面润湿性的强弱是影响壁面吸附流体分子的主要影响因素.Heat transfer in a micro-scale system has less thermal inertia and faster thermal response, which has unique advantages in controlling heat transfer. Interface thermal resistance is an important physical quantity that reflects the heat transfer performance of the interface on a micro-scale. In this paper, the interface thermal resistance os static fluid and flowing fluid in nanochannel, which are different in the wall temperature and wettability, are studied by the molecular dynamics method. In the static fluid, the results show that the wall wettability has a significant influence on the interface thermal resistance, and the stronger the wall wettability, the smaller the values of interface thermal resistance is. For the walls with different temperatures, it can be observed that the interface thermal resistance on high temperature wall is higher than that on low temperature, when the wall wettability is weaker. On the contrary, when the wall wettability is stronger, the effect of wall temperatures on the interface thermal resistance is negligible. An external force applied to the fluid domain makes the fluid flow. In the flowing fluid, the results show that the variation of wall wettability and external force can lead to the slip to different degrees at the interface, and the slip-induced frictional viscous heat is generated at the solid-liquid interface, and thus increasing the fluid temperature and the heat flux of the system. The effect of external force on the thermal resistance is limited by the wall wettability. When the wall wettability is weaker, the increase of the external force will make the interface slip more easily and the thermal resistance decrease. With the stronger wall wettability, it is difficult to make the interface slip obviously with the increase of external force, and the influence of external force on interface thermal resistance decreases. The heat transfer performance at the solid-liquid interface is related to the number of fluid molecules adsorbed on the wall surface. The results show that in the static fluid, the increase of wall wettability will make more fluid molecules adsorbed on the wall, and the arrangement becomes more and more regular, which causes the interface thermal resistance to decrease and is beneficial to the interface heat transfer. In the flowing fluid, the change of external force has less influence on the number of adsorbed molecules, and the wall wettability is the main factor affecting the adsorption of fluid molecules on the wall.
-
Keywords:
- wettability /
- external force /
- interface thermal resistance /
- molecular dynamics
[1] 范世福 2007 现代科学仪器 5 17
Google Scholar
Fan S F 2007 Modern Scientific Instruments 5 17
Google Scholar
[2] 张锡奇, 闻利平, 江雷 2019 68 018801
Google Scholar
Zhang X Q, Wen L P, Jiang L 2019 Acta Phys. Sin. 68 018801
Google Scholar
[3] 唐琼辉 2008 博士学位论文 (合肥: 中国科学技术大学)
Tang Q H 2008 Ph. D. Dissertation (Hefei: University of Science And Technology of China) (in Chinese)
[4] 赵素, 李金富, 周尧和 2007 材料导报 21 5
Google Scholar
Zhao S, Li J F, Zhou Y H 2007 Mater. Rep. 21 5
Google Scholar
[5] Ge Z B, Cahill D G, Braun P V 2006 Phys. Rev. Lett. 96 186101
Google Scholar
[6] Stevens R J, Zhigilei L V, Norris P M 2007 Int. J. Heat Mass Transfer 50 3977
Google Scholar
[7] Liu C, Fan H B, Zhang K, Yuen M, Li Z G 2010 J. Chem. Phys. 132 094703
Google Scholar
[8] 葛宋, 陈民 2013 62 110204
Google Scholar
Ge S, Chen M 2013 Acta Phys. Sin. 62 110204
Google Scholar
[9] 周璐, 马红和 2019 工程热 11 2603
Zhou L, Ma H H 2019 J. Eng. Therm. 11 2603
[10] Chiloyan V, Garg J, Esfarjani K, Chen G 2015 Nat. Commun. 6 6755
Google Scholar
[11] 张龙艳, 徐进良, 雷俊鹏 2019 62 020201
Google Scholar
Zhang L Y, Xu J L, Lei J P 2019 Acta Phys. Sin. 62 020201
Google Scholar
[12] Shi Z, Barisik M, Beskok A 2012 Int. J. Therm. Sci. 59 29
Google Scholar
[13] Barisik M, Beskok A 2012 J. Comput. Phys. 231 7881
Google Scholar
[14] 张程宾, 许兆林, 陈永平 2014 63 263
Zhang C B, Xu Z L, Chen Y P 2014 Acta Phys. Sin. 63 263
[15] Li Z G 2009 Phys. Rev. E 79 026312
Google Scholar
[16] 胡海豹, 鲍路瑶, 黄苏和 2013 力学学报 45 507
Google Scholar
Hu H B, Bao L Y, Huang S H 2013 Chin. J. Theor. Appl. Mech. 45 507
Google Scholar
[17] Wang X, Jing D W 2019 Int. J. Heat Mass Transfer 128 199
Google Scholar
[18] Guo Y T, Surblys D, Kawagoe Y, Matsubara H, Liu X, Ohara T 2019 Int. J. Heat Mass Transfer 135 115
Google Scholar
[19] Toghraie D, Mokhtari M, Afrand M 2016 Physica E 84 152
Google Scholar
[20] Plimpton S 1995 J. Comput. Phys. 117 1
Google Scholar
[21] Liang Z, Tsai H L 2011 Phys. Rev. E 83 061603
[22] Wang X, Cheng P, Quan X 2016 Int. Commun. Heat Mass Transfer 77 183
Google Scholar
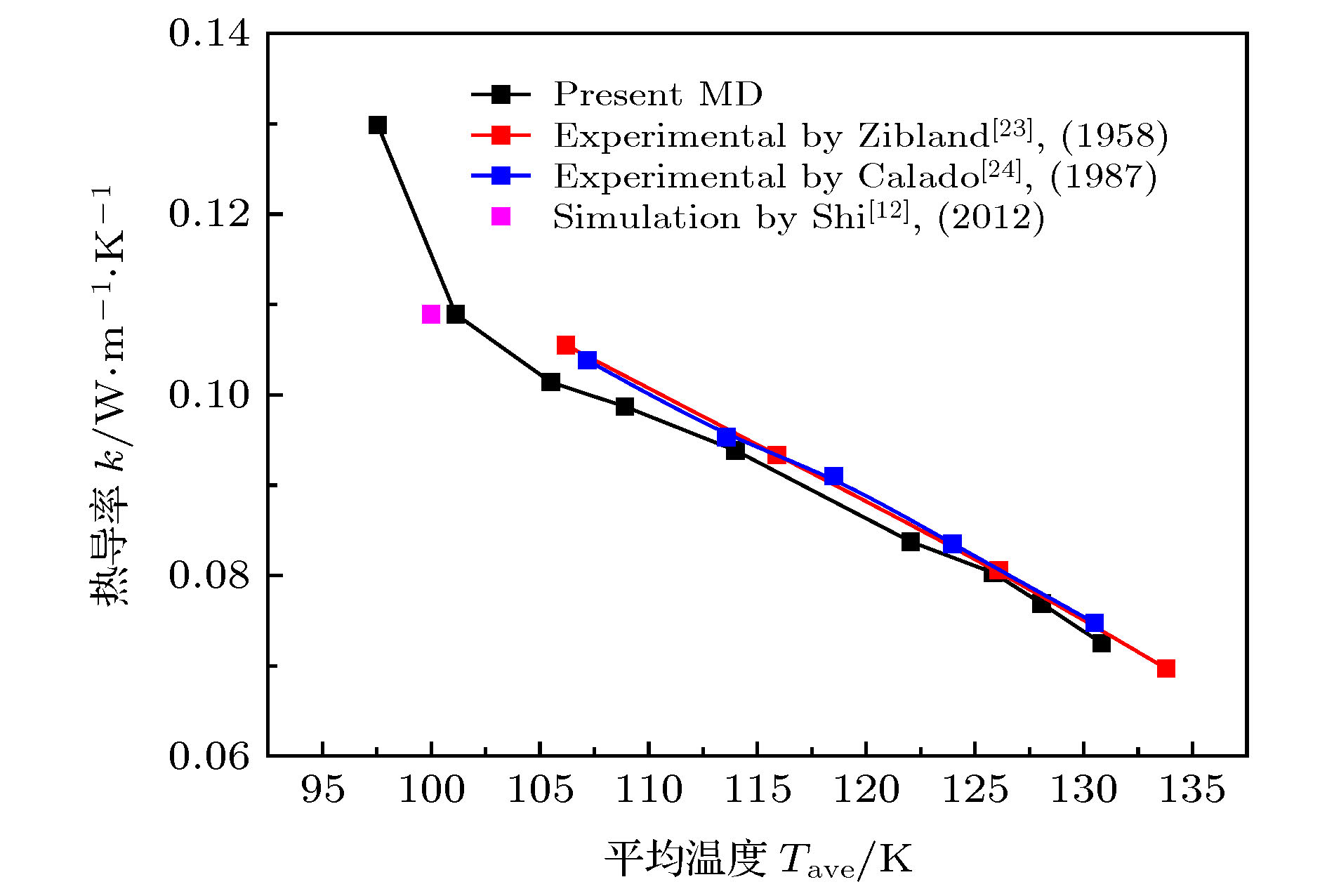
[23] Ziebland H, Burton J T A 1958 Br. J. Appl. Phys. 9 52
Google Scholar
[24] Calado J C G, Mardolacr U V, Castro C A N D 1987 Physica A 143 314
Google Scholar
-
图 2 固液界面处流体温度的预测
Fig. 2. Prediction of fluid temperature at the solid-liquid interface.
图 3 液态氩在不同固液势能强度εwf/ε下的温度分布 (a)工况1; (b)工况2
Fig. 3. Temperature distribution of liquid argon at different solid-liquid potential energy εwf/ε: (a) Condition 1; (b) condition 2.
图 4 (a)工况1中近热壁面附近流体数密度分布; (b)工况2中近冷壁面附近流体数密度分布
Fig. 4. (a) Number density distribution near the hot wall surface in condition 1; (b) number density distribution near the cold wall surface in condition 2.
图 5 固液势能强度对温度跳跃的影响
Fig. 5. Effect of solid-liquid potential energy on temperature jump.
图 6 固液势能强度对系统热通量的影响
Fig. 6. Effect of solid-liquid potential energy on heat flux of system.
图 7 固液势能强度对界面热阻的影响
Fig. 7. Effect of solid-liquid potential energy on interface thermal resistance.
图 9 固液势能强度对壁面吸附流体分子数的影响
Fig. 9. Effect of solid-liquid potential energy on the number of fluid molecules adsorbed on the wall surface.
图 12 工况1中液体氩在不同外力作用下的速度分布 (a) F = 0.01ε/σ; (b) F = 0.012ε/σ; (c) F = 0.014ε/σ; (d) F = 0.016ε/σ
Fig. 12. Velocity distribution of liquid argon under different external forces in condition 1: (a) F = 0.01ε/σ; (b) F = 0.012ε/σ; (c) F = 0.014ε/σ; (d) F = 0.016ε/σ
图 13 工况1中液体氩在不同外力作用下的温度分布 (a) F = 0.01ε/σ; (b) F = 0.012ε/σ; (c) F = 0.014ε/σ; (d) F = 0.016ε/σ
Fig. 13. Temperature distribution of liquid argon under different external forces in condition 1: (a) F = 0.01ε/σ; (b) F = 0.012ε/σ; (c) F = 0.014ε/σ; (d) F = 0.016ε/σ.
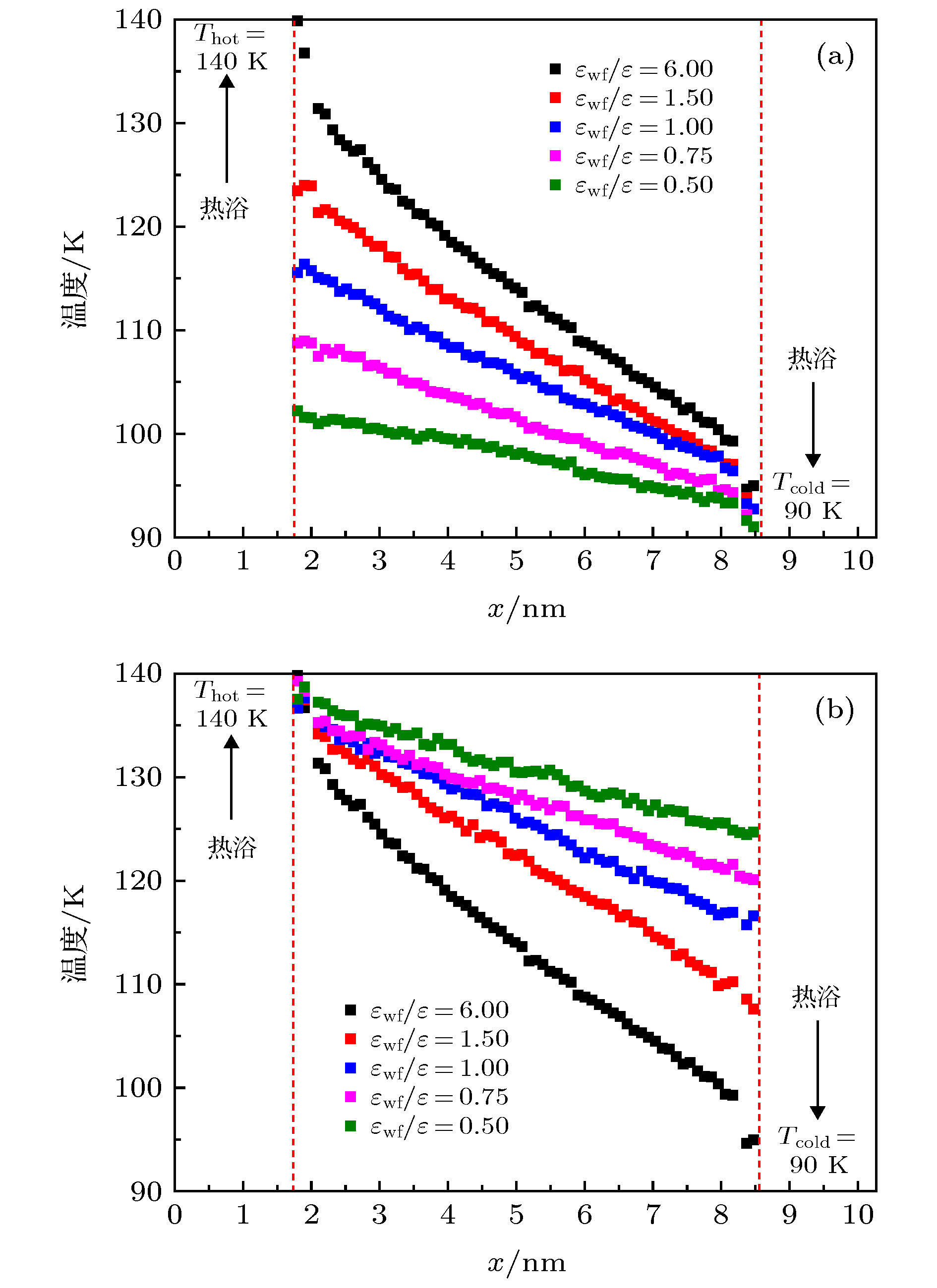
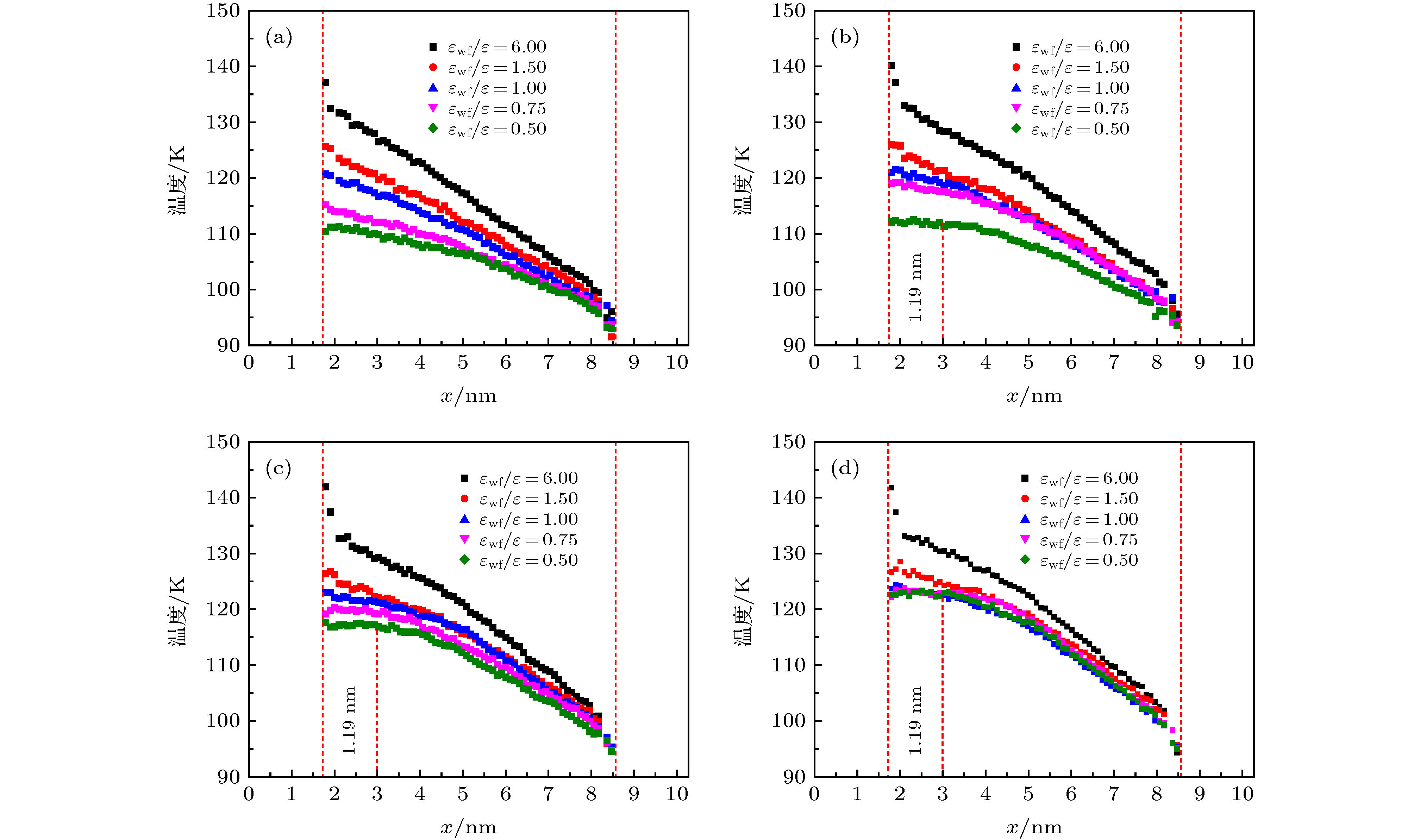
图 14 工况1中液体氩在不同固液势能强度下的温度分布 (a) εwf/ε = 6.0; (b) εwf/ε = 1.5; (c) εwf/ε = 1.0; (d) εwf/ε = 0.75; (e) εwf/ε = 0.5
Fig. 14. Temperature distribution of liquid argon under different solid-liquid potential energy intensity: (a) εwf/ε = 6.0; (b) εwf/ε = 1.5; (c) εwf/ε = 1.0; (d) εwf/ε = 0.75; (e) εwf/ε = 0.5.
图 15 不同外力作用下近热壁面局部(1.19 nm)平均温度分布
Fig. 15. Local (1.19 nm) average temperature distribution near the hot wall under different external forces.
图 16 近热壁面处液态氩的速度分布
Fig. 16. Velocity distribution of liquid argon near the hot wall surface.
图 17 外力作用下固液势能强度比对系统热通量的影响
Fig. 17. Effect of solid-liquid potential energy on system heat flux under external force
图 18 工况1中不同外力作用下固液势能强度对温度跳跃的影响 (a) 热壁面; (b) 冷壁面
Fig. 18. Effect of solid-liquid potential energy on temperature jump under different external forces in condition 1: (a) Hot wall surface; (b) cold wall surface.
图 19 工况1中不同外力作用下固液势能强度对界面热阻的影响 (a) 热壁面; (b) 冷壁面
Fig. 19. Effect of solid-liquid potential energy on interface thermal resistance under different external forces in condition 1: (a) Hot wall surface; (b) cold wall surface.
图 20 动态流体中热壁面吸附流体分子数
Fig. 20. The number of adsorbed fluid molecules on the hot wall in flowing fluid.
表 1 模拟工况
Table 1. Simulated conditions
模拟工况 壁面温度 固液势能强度εwf/ε 工况1 热壁面(140 K) 6.0 1.5 1.0 0.75 0.5 冷壁面(90 K) 6.0 6.0 6.0 6.0 6.0 工况2 热壁面(140 K) 6.0 6.0 6.0 6.0 6.0 冷壁面(90 K) 6.0 1.5 1.0 0.75 0.5 
下载: 导出CSV
表 2 不同固液势能强度下对应的接触角
Table 2. Corresponding contact angle under different solid-liquid potential energy intensity
εwf/ε 6.0 1.5 1.0 0.75 0.5 θ/(°) 0 0 0 60 90
下载: 导出CSV
-
[1] 范世福 2007 现代科学仪器 5 17
Google Scholar
Fan S F 2007 Modern Scientific Instruments 5 17
Google Scholar
[2] 张锡奇, 闻利平, 江雷 2019 68 018801
Google Scholar
Zhang X Q, Wen L P, Jiang L 2019 Acta Phys. Sin. 68 018801
Google Scholar
[3] 唐琼辉 2008 博士学位论文 (合肥: 中国科学技术大学)
Tang Q H 2008 Ph. D. Dissertation (Hefei: University of Science And Technology of China) (in Chinese)
[4] 赵素, 李金富, 周尧和 2007 材料导报 21 5
Google Scholar
Zhao S, Li J F, Zhou Y H 2007 Mater. Rep. 21 5
Google Scholar
[5] Ge Z B, Cahill D G, Braun P V 2006 Phys. Rev. Lett. 96 186101
Google Scholar
[6] Stevens R J, Zhigilei L V, Norris P M 2007 Int. J. Heat Mass Transfer 50 3977
Google Scholar
[7] Liu C, Fan H B, Zhang K, Yuen M, Li Z G 2010 J. Chem. Phys. 132 094703
Google Scholar
[8] 葛宋, 陈民 2013 62 110204
Google Scholar
Ge S, Chen M 2013 Acta Phys. Sin. 62 110204
Google Scholar
[9] 周璐, 马红和 2019 工程热 11 2603
Zhou L, Ma H H 2019 J. Eng. Therm. 11 2603
[10] Chiloyan V, Garg J, Esfarjani K, Chen G 2015 Nat. Commun. 6 6755
Google Scholar
[11] 张龙艳, 徐进良, 雷俊鹏 2019 62 020201
Google Scholar
Zhang L Y, Xu J L, Lei J P 2019 Acta Phys. Sin. 62 020201
Google Scholar
[12] Shi Z, Barisik M, Beskok A 2012 Int. J. Therm. Sci. 59 29
Google Scholar
[13] Barisik M, Beskok A 2012 J. Comput. Phys. 231 7881
Google Scholar
[14] 张程宾, 许兆林, 陈永平 2014 63 263
Zhang C B, Xu Z L, Chen Y P 2014 Acta Phys. Sin. 63 263
[15] Li Z G 2009 Phys. Rev. E 79 026312
Google Scholar
[16] 胡海豹, 鲍路瑶, 黄苏和 2013 力学学报 45 507
Google Scholar
Hu H B, Bao L Y, Huang S H 2013 Chin. J. Theor. Appl. Mech. 45 507
Google Scholar
[17] Wang X, Jing D W 2019 Int. J. Heat Mass Transfer 128 199
Google Scholar
[18] Guo Y T, Surblys D, Kawagoe Y, Matsubara H, Liu X, Ohara T 2019 Int. J. Heat Mass Transfer 135 115
Google Scholar
[19] Toghraie D, Mokhtari M, Afrand M 2016 Physica E 84 152
Google Scholar
[20] Plimpton S 1995 J. Comput. Phys. 117 1
Google Scholar
[21] Liang Z, Tsai H L 2011 Phys. Rev. E 83 061603
[22] Wang X, Cheng P, Quan X 2016 Int. Commun. Heat Mass Transfer 77 183
Google Scholar
[23] Ziebland H, Burton J T A 1958 Br. J. Appl. Phys. 9 52
Google Scholar
[24] Calado J C G, Mardolacr U V, Castro C A N D 1987 Physica A 143 314
Google Scholar
下载:
计量
- 文章访问数: 6103
- PDF下载量: 116
- 被引次数: 0
