-
In this paper, a four-terminal hybrid driven refrigerator model with three capacitively coupled quantum dots is proposed, which can be driven by the energy current injected from the highest temperature thermal reservoir and the power input to achieve the refrigeration of the low temperature reservoir. Based on the master equation we derive the expressions for charge current and heat current between three quantum dots and thermal reservoirs in the weak/strong capacitive coupling case, respectively. We numerically analyze the thermodynamic performance characteristics of the refrigerator between the cooling rate and the coefficient of performance, and the main performance parameters of the refrigerator are optimized under the condition of the maximum cooling rate. Finally, we compare the performance of this refrigerator in the strong capacitive coupling case with that in the weak capacitive coupling case.
-
Keywords:
- couple quantum dot /
- four-terminal hybrid refrigerator /
- cooling rate /
- coefficient of performance
[1] Chen L, Ding Z, Sun F 2011 Energy 36 4011
Google Scholar
[2] Sánchez R, Büttiker M 2011 Phys. Rev. B 83 085428
Google Scholar
[3] Thierschmann H, Sánchez R, Sothmann B, Arnold F, Heyn C, Hansen W, Buhmann H, Molenkamp L W 2015 Nat. Nanotechnol 10 854
Google Scholar
[4] Zhang Y C, Lin G X, Chen J C 2015 Phys. Rev. E 91 052118
Google Scholar
[5] Zhang Y C, Huang C K, Lin G X, Chen J C 2015 Energy 85 200
Google Scholar
[6] Zhang Y C, Wang Y, Huang C K, Lin G X, Chen J C 2016 Energy 95 593
Google Scholar
[7] Aniket S. 2020 J. Appl. Phys 127 234903
Google Scholar
[8] Anamika B, Surojit H, Shailendra K, Varshney, Gourab D, Aniket S 2021 Phys. Rev. E 103 012131
Google Scholar
[9] Kano S, Fujii M 2017 Nanotechnology 28 095403
Google Scholar
[10] Lim J S, Sánchez D, López R 2018 N. J. Phys. 20 023038
Google Scholar
[11] Daré A M, Lombardo P 2017 Phys. Rev. B 96 115414
Google Scholar
[12] Su H, Shi Z C, He J Z 2015 Chin. Phys. Lett. 32 100501
Google Scholar
[13] 苏豪, 王家伟, 赵沁园, 何济洲 2016 中国科学: 技术科学 46 1296
Google Scholar
Su H, Wang J W, Zhao Q Y, He J Z 2016 Sci. Sin-Tech. 46 1296
Google Scholar
[14] Shi Z C, Qin W F, He J Z 2016 Mod. Phys. Lett. B 30 1650397
Google Scholar
[15] Roche B, Roulleau P, Jullien T, Jompol, Y, Farrer I, Ritchie D A, Glattli D C. 2015 Nat. Commun 6 6738
Google Scholar
[16] Hartmann F, Pfeffer P, Höfling S, Kamp M, Worschech L. 2015 Phys. Rev. Lett. 114 146805
Google Scholar
[17] Josefsson M, Svilans A, Burke A, Hoffmann E, Fahlvik S, Thelander C, Leijnse M, Linke H 2018 Nat. Nanotechnol 13 920
Google Scholar
[18] Keller A J, Lim J S, Sánchez D, López R, Amasha S, Katine J A 2016 Phys. Rev. Lett. 117 066602
Google Scholar
[19] Sothmann B, Sánchez R, Jordan A N, Büttiker M 2013 N. J. Phys. 15 095021
Google Scholar
[20] Choi Y, Jordan A N 2015 Physica E:Low-dimensional Systems Nanostruct 74 465
Google Scholar
[21] Lin Z B, Yang Y Y, Fu J, Li W, He J Z 2019 Chin. Phys. Lett. 36 060501
Google Scholar
[22] Lin Z B, Li W, Yang Y Y, He J Z 2020 Phys. Rev. E 101 022117
Google Scholar
[23] Sothmann B, Sánchez R, Jordan A N 2014 Europhys. Lett. 107 47003
Google Scholar
[24] Sánchez R, Sothmann B, Jordan A N 2015 Phys. Rev. Lett. 114 146801
Google Scholar
[25] Boukai A I, Bunimovich Y, Tahir-Kheli J, Yu J K, Goddard I W A, Heath J R 2008 Nature 451 168
Google Scholar
[26] Yang Y Y, Xu S, Li W, He J Z 2020 Phys. Scr. 95 095001
Google Scholar
[27] Yang Y Y, Xu S, He J Z 2020 Chin. Phys. Lett. 37 120502
Google Scholar
[28] Su S, Zhang Y, Chen J, Shih T M 2016 Sci. Reports 6 21425
Google Scholar
[29] Shi Z C, Fu J, Qin W F, He J Z 2017 Chin. Phys. Lett. 34 110501
Google Scholar
[30] Jiang J H, Entin-Wohlman O, Imry Y 2013 New Journal of Physics 15 075021
Google Scholar
[31] Li C, Zhang Y, He J 2013 Chin. Phys. Lett. 30 100501
Google Scholar
[32] Rutten B, Esposito M, Cleuren B 2009 Phys. Rev. B 80 235122
Google Scholar
[33] Cleuren B, Rutten B, Van den Broeck C 2012 Phys. Rev. Lett. 108 120603
Google Scholar
[34] 施志诚, 何济洲, 肖宇玲 2015 中国科学: 物理学 力学 天文学 45 050502
Google Scholar
Shi Z C, He J Z, Xiao Y L 2015 Sci. Sin-Phys. Mech. Astron. 45 050502
Google Scholar
[35] Li C, Zhang Y, Wang J, He J 2013 Phys. Rev. E 88 062120
Google Scholar
[36] Wang J H, Lai Y M, Ye Z L, He J Z, Ma Y L, Liang Q H 2015 Phys. Rev. E 91 050102
Google Scholar
[37] 李唯, 符婧, 杨贇贇, 何济洲 2019 68 220501
Google Scholar
Li W, Fu J, Yang Y Y, He J Z 2019 Acta Phys. Sin. 68 220501
Google Scholar
[38] Whitney R S, Sánchez R, Haupt F, Splettstoesser J 2016 Phys. E 82 176
Google Scholar
[39] Fu T, Du J Y, Su S H, Su G Z, Chen J C 2021 Eur. Phys. J. Plus 136 1059
Google Scholar
[40] Xi M M, Wang R Q, Lu J C, Chen T Y, Jiang J H 2021 Chin. Phys. Lett 38 088801
Google Scholar
[41] 苏山河, 张艳超, 彭万里, 苏国珍, 陈金灿 2021 中国科学: 物理学 力学 天文学 51 112
Google Scholar
Su S H, Zhang Y C, Peng W L, Su G Z, Chen J C 2021 Sci. Sin-Phys. Mech. Astron. 51 112
Google Scholar
-
图 1 (a) 基于三量子点耦合的四端制冷机的示意图; (b) (a)中装置的等效电路图
Figure 1. (a) Schematic diagram of a four terminal refrigerator based on three coupled quantum dots, and (b) is the equivalent circuit diagram of the device in (a).
图 3 当耗散系数为
$ \lambda = 0 $ 时, (a) 输入功率$ P $ 以及(b)—(d)各量子点与对应库之间的热流JH, JC, JLR随温差$ \Delta T $ 和偏置电压$ e\Delta V $ 变化的三维投影图Figure 3. The three-dimensional projection graphs for (a) input power
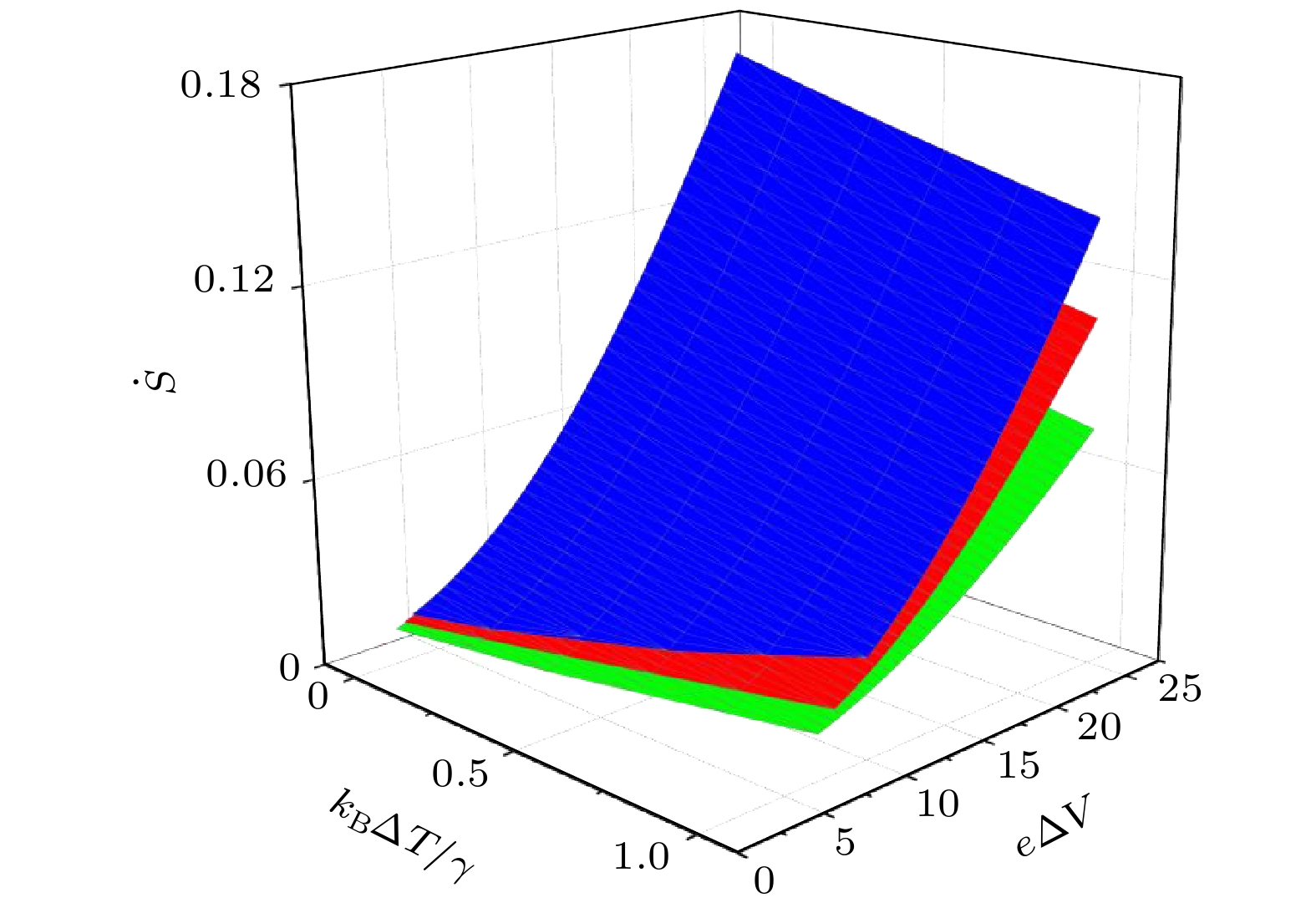
$ P $ and (b)–(d) the heat flow JH, JC, JLR varying with the temperature difference$ \Delta T $ and the bias voltage$ e\Delta V $ under the dissipation factor$ \lambda = 0 $ .
图 4 当耗散系数为
$ \lambda = 0 $ 和$ \lambda = 0.26 $ 时, 装置A和装置B各自对应的工作区域Figure 4. The corresponding working areas of device A and device B when the dissipation factor is (a)
$ \lambda = 0 $ and (b)$ \lambda = 0.26 $ , respectively.
图 5 在不同耗散系数下, 装置作为混合驱动制冷机时的总熵产率随温差
$ \Delta T $ 和偏置电压$ e\Delta V $ 变化的三维曲线Figure 5. The three-dimensional curves of total entropy production rate varying with temperature difference
$ \Delta T $ and bias voltage$ e\Delta V $ when the device is used as a hybrid-driven refrigerator under different dissipation factor.
图 6 在不同耗散系数下, 制冷率和制冷系数随充电能
$ {U_{{\text{MH}}}} $ 和$ {U_{{\text{MC}}}} $ 变化的三维图Figure 6. The three-dimensional diagrams of the cooling rate and the COP varying with charging energy
$ {U_{{\text{MH}}}} $ and$ {U_{{\text{MC}}}} $ under different dissipation factor.
图 7 在不同的耗散系数下, 制冷率和制冷系数随充电能
$ {U_{{\text{MH}}}} $ 和偏置电压$ eV $ 变化的三维图Figure 7. The three-dimensional diagrams of the cooling rate and the COP varying with charging energy
$ {U_{{\text{MH}}}} $ and bias voltage$ e\Delta V $ under different dissipation factor.
图 8 在给定条件
$ \Delta T = 2\gamma /{k_{\text{B}}} $ 下, (a) 优化的制冷率$ {J_{{\text{Copt}}}} $ 和(b)优化制冷率对应的制冷系数以及(c)对应的充电能$ {U_{{\text{MC}}}} $ 随耗散系数$ \lambda $ 的变化曲线Figure 8. The curves of (a) the optimized cooling rate
$ {J_{{\text{Copt}}}} $ and (b) the COP corresponding to optimized cooling rate and (c) the corresponding charging energy$ {U_{{\text{MC}}}} $ as a function of dissipation factor$ \lambda $ under the given condition$ \Delta T = 2\gamma /{k_{\text{B}}} $ .
图 9 (a) 最大制冷率
$ {J_{{\text{C}}\max }} $ 和最大制冷率对应的COP$ {\eta _{\text{J}}} $ ; (b) 最佳充电能量$ {U_{{\text{MC}}}} $ 随温差$ \Delta T $ 的变化曲线Figure 9. The curves of (a) the maximum cooling rate
$ {J_{{\text{C}}\max }} $ and the COP corresponding to maximum cooling rate$ {\eta _{\text{J}}} $ and (b) the optimal charging energy$ {U_{{\text{MC}}}} $ as a function of temperature difference$ \Delta T $ .
图 10 在强耦合
$ {U_{{\text{HC}}}} $ 的情况下, 当$ \lambda = 0 $ 时, (a) 制冷率$ {J_{\text{C}}} $ 和(b)制冷系数$ {\eta _{{\text{COP}}}} $ 随着$ {U_{{\text{MH}}}} $ 和$ {U_{{\text{MC}}}} $ 变化的三维图Figure 10. In the case of strong coupling
$ {U_{{\text{HC}}}} $ , when$ \lambda = 0 $ , the three-dimensional diagrams for (a) cooling rate$ {J_{\text{C}}} $ and (b) the COP varying with$ {U_{{\text{MH}}}} $ and$ {U_{{\text{MC}}}} $ . -
[1] Chen L, Ding Z, Sun F 2011 Energy 36 4011
Google Scholar
[2] Sánchez R, Büttiker M 2011 Phys. Rev. B 83 085428
Google Scholar
[3] Thierschmann H, Sánchez R, Sothmann B, Arnold F, Heyn C, Hansen W, Buhmann H, Molenkamp L W 2015 Nat. Nanotechnol 10 854
Google Scholar
[4] Zhang Y C, Lin G X, Chen J C 2015 Phys. Rev. E 91 052118
Google Scholar
[5] Zhang Y C, Huang C K, Lin G X, Chen J C 2015 Energy 85 200
Google Scholar
[6] Zhang Y C, Wang Y, Huang C K, Lin G X, Chen J C 2016 Energy 95 593
Google Scholar
[7] Aniket S. 2020 J. Appl. Phys 127 234903
Google Scholar
[8] Anamika B, Surojit H, Shailendra K, Varshney, Gourab D, Aniket S 2021 Phys. Rev. E 103 012131
Google Scholar
[9] Kano S, Fujii M 2017 Nanotechnology 28 095403
Google Scholar
[10] Lim J S, Sánchez D, López R 2018 N. J. Phys. 20 023038
Google Scholar
[11] Daré A M, Lombardo P 2017 Phys. Rev. B 96 115414
Google Scholar
[12] Su H, Shi Z C, He J Z 2015 Chin. Phys. Lett. 32 100501
Google Scholar
[13] 苏豪, 王家伟, 赵沁园, 何济洲 2016 中国科学: 技术科学 46 1296
Google Scholar
Su H, Wang J W, Zhao Q Y, He J Z 2016 Sci. Sin-Tech. 46 1296
Google Scholar
[14] Shi Z C, Qin W F, He J Z 2016 Mod. Phys. Lett. B 30 1650397
Google Scholar
[15] Roche B, Roulleau P, Jullien T, Jompol, Y, Farrer I, Ritchie D A, Glattli D C. 2015 Nat. Commun 6 6738
Google Scholar
[16] Hartmann F, Pfeffer P, Höfling S, Kamp M, Worschech L. 2015 Phys. Rev. Lett. 114 146805
Google Scholar
[17] Josefsson M, Svilans A, Burke A, Hoffmann E, Fahlvik S, Thelander C, Leijnse M, Linke H 2018 Nat. Nanotechnol 13 920
Google Scholar
[18] Keller A J, Lim J S, Sánchez D, López R, Amasha S, Katine J A 2016 Phys. Rev. Lett. 117 066602
Google Scholar
[19] Sothmann B, Sánchez R, Jordan A N, Büttiker M 2013 N. J. Phys. 15 095021
Google Scholar
[20] Choi Y, Jordan A N 2015 Physica E:Low-dimensional Systems Nanostruct 74 465
Google Scholar
[21] Lin Z B, Yang Y Y, Fu J, Li W, He J Z 2019 Chin. Phys. Lett. 36 060501
Google Scholar
[22] Lin Z B, Li W, Yang Y Y, He J Z 2020 Phys. Rev. E 101 022117
Google Scholar
[23] Sothmann B, Sánchez R, Jordan A N 2014 Europhys. Lett. 107 47003
Google Scholar
[24] Sánchez R, Sothmann B, Jordan A N 2015 Phys. Rev. Lett. 114 146801
Google Scholar
[25] Boukai A I, Bunimovich Y, Tahir-Kheli J, Yu J K, Goddard I W A, Heath J R 2008 Nature 451 168
Google Scholar
[26] Yang Y Y, Xu S, Li W, He J Z 2020 Phys. Scr. 95 095001
Google Scholar
[27] Yang Y Y, Xu S, He J Z 2020 Chin. Phys. Lett. 37 120502
Google Scholar
[28] Su S, Zhang Y, Chen J, Shih T M 2016 Sci. Reports 6 21425
Google Scholar
[29] Shi Z C, Fu J, Qin W F, He J Z 2017 Chin. Phys. Lett. 34 110501
Google Scholar
[30] Jiang J H, Entin-Wohlman O, Imry Y 2013 New Journal of Physics 15 075021
Google Scholar
[31] Li C, Zhang Y, He J 2013 Chin. Phys. Lett. 30 100501
Google Scholar
[32] Rutten B, Esposito M, Cleuren B 2009 Phys. Rev. B 80 235122
Google Scholar
[33] Cleuren B, Rutten B, Van den Broeck C 2012 Phys. Rev. Lett. 108 120603
Google Scholar
[34] 施志诚, 何济洲, 肖宇玲 2015 中国科学: 物理学 力学 天文学 45 050502
Google Scholar
Shi Z C, He J Z, Xiao Y L 2015 Sci. Sin-Phys. Mech. Astron. 45 050502
Google Scholar
[35] Li C, Zhang Y, Wang J, He J 2013 Phys. Rev. E 88 062120
Google Scholar
[36] Wang J H, Lai Y M, Ye Z L, He J Z, Ma Y L, Liang Q H 2015 Phys. Rev. E 91 050102
Google Scholar
[37] 李唯, 符婧, 杨贇贇, 何济洲 2019 68 220501
Google Scholar
Li W, Fu J, Yang Y Y, He J Z 2019 Acta Phys. Sin. 68 220501
Google Scholar
[38] Whitney R S, Sánchez R, Haupt F, Splettstoesser J 2016 Phys. E 82 176
Google Scholar
[39] Fu T, Du J Y, Su S H, Su G Z, Chen J C 2021 Eur. Phys. J. Plus 136 1059
Google Scholar
[40] Xi M M, Wang R Q, Lu J C, Chen T Y, Jiang J H 2021 Chin. Phys. Lett 38 088801
Google Scholar
[41] 苏山河, 张艳超, 彭万里, 苏国珍, 陈金灿 2021 中国科学: 物理学 力学 天文学 51 112
Google Scholar
Su S H, Zhang Y C, Peng W L, Su G Z, Chen J C 2021 Sci. Sin-Phys. Mech. Astron. 51 112
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 4293
- PDF Downloads: 65
- Cited By: 0
