用于亚开温区的极低温绝热去磁制冷机

王昌; 李珂; 沈俊; 戴巍; 王亚男; 罗二仓; 沈保根; 周远

doi:10.7498/aps.70.20202237

摘要

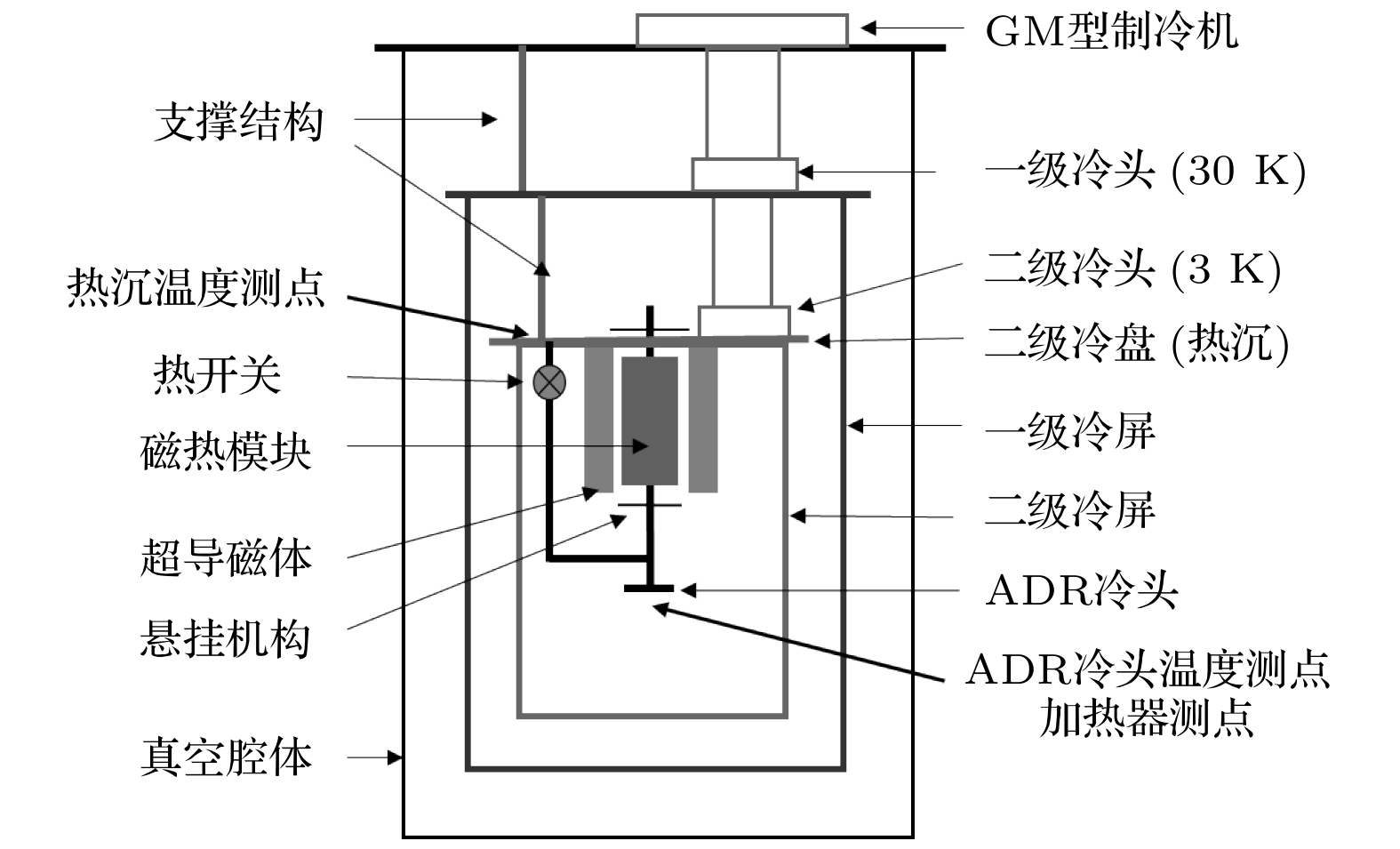
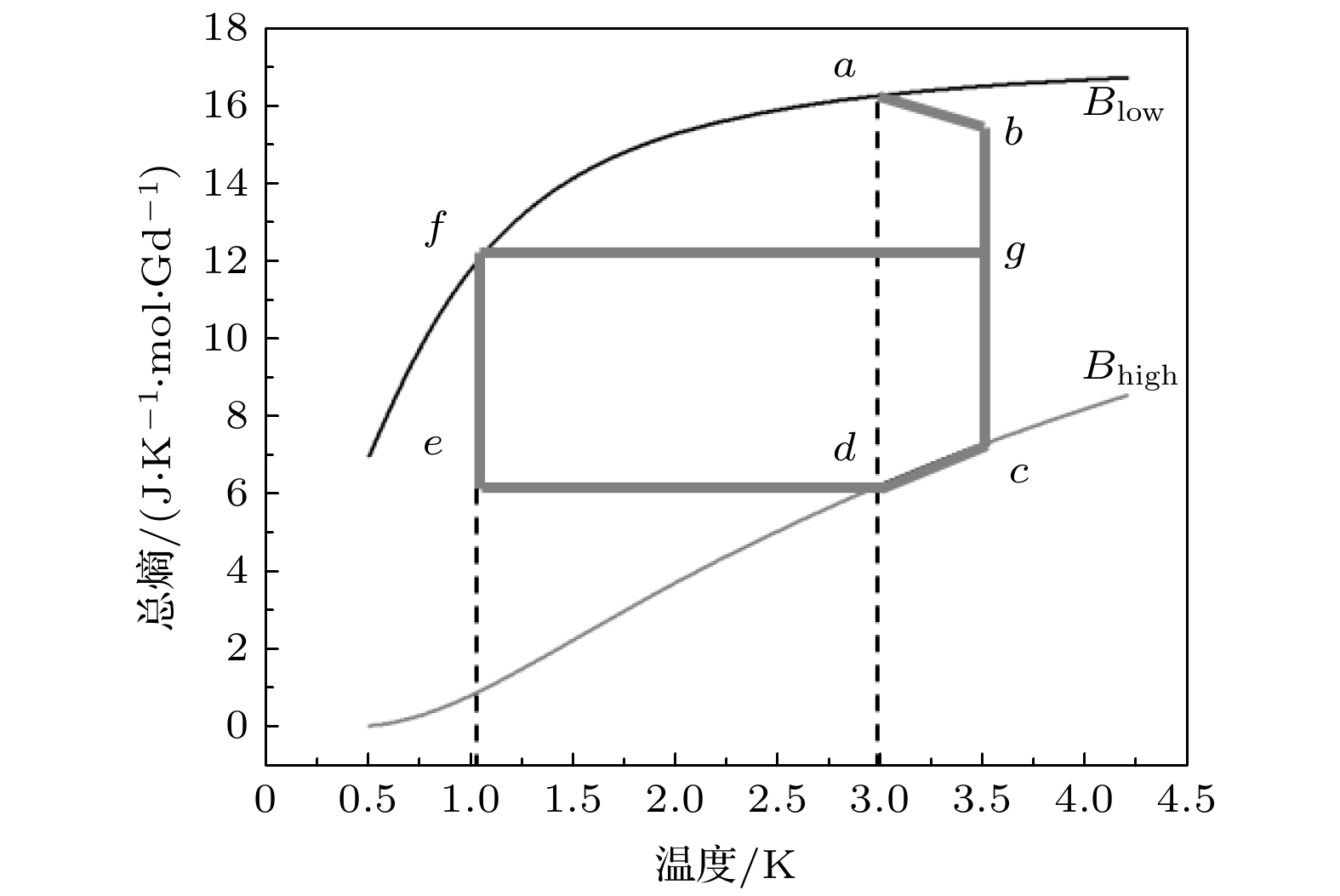
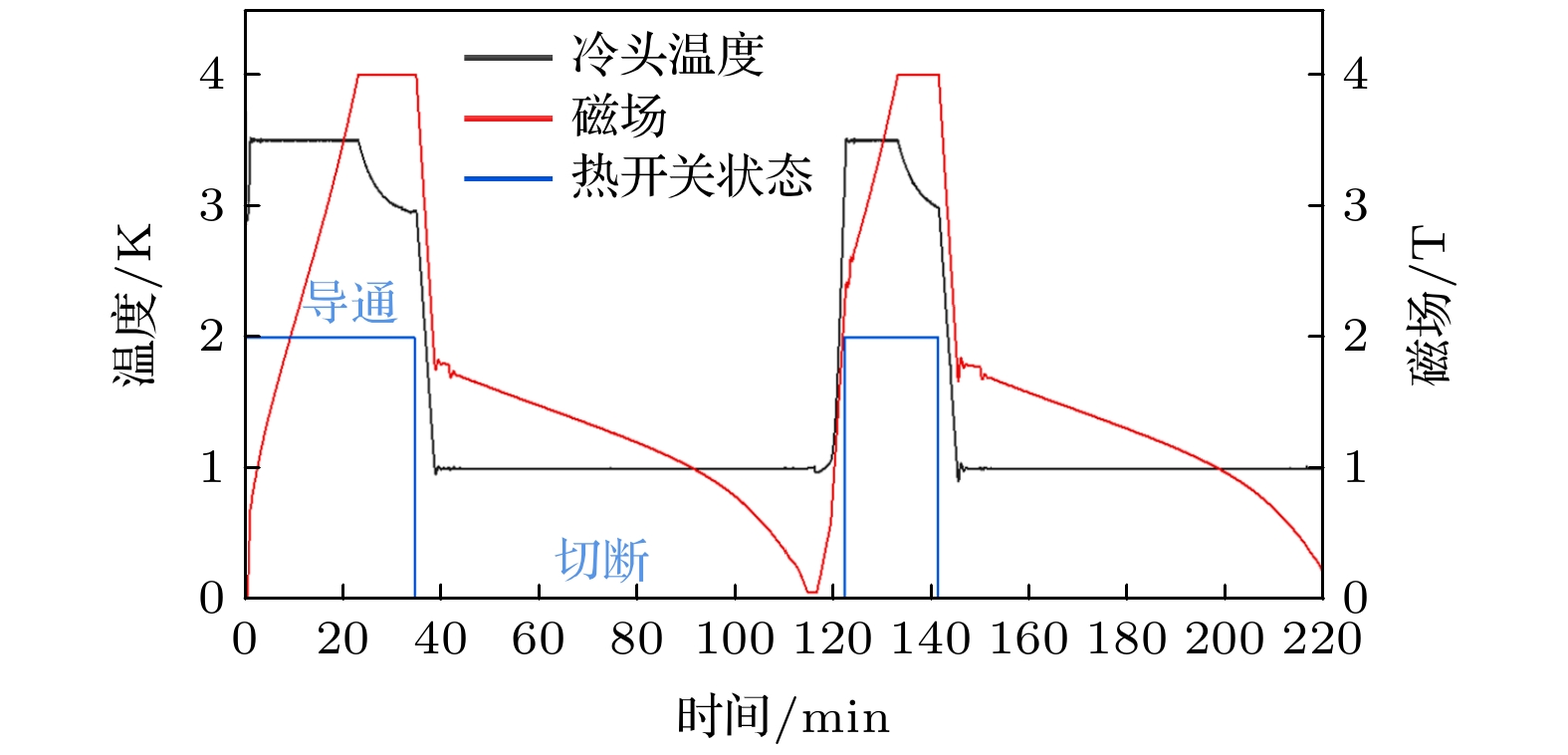
随着空间观测、量子技术等前沿科研领域的发展, 亚开温区的极低温制冷需求日益增加. 本文设计并研制了一台极低温单级绝热去磁制冷机. 该制冷机由GM型制冷机提供约3 K热沉, 以钆镓石榴石为磁热工质, 由超导线圈提供最大为4 T的磁场, 通过绝热去磁, 实验最低温度可达470 mK. 在恒温控制模式下, 可在1 K下提供2.7 J冷量, 温度波动小于0.5 mK, 绝热去磁制冷的第二热力学效率为57%; 在0.8 K下, 制冷量为1.2 J. 该制冷机将作为50 mK温区三级绝热去磁制冷系统中的第一级, 在1 K下提供0.7 mW制冷功率. 本研究为进一步开展极低温多级连续绝热去磁制冷奠定了基础.

关键词:

Abstract

With the development of space observation, quantum technology and other frontier scientific research fields, the demand for ultra-low temperature refrigeration in sub-Kelvin region is increasing. Compared with dilution refrigeration and sorption refrigeration, adiabatic demagnetization refrigeration (ADR) has the outstanding advantages of high efficiency, compact, gravity independence and accessibility of working materials, which make ADR a promising technology for sub-Kelvin cooling.A single-stage ultro-low temperature adiabatic demagnetization refrigerator is designed and developed. The thermodynamic principle and quantitative analysis are presented, from the macroscopic and microcosmic view, and operating results show good agreement with the theoretical value.This refrigerator is precooled to 3 K by a GM-type refrigerator, with 252 g gadolinium gallium garnet (monocrystalline) used as a working medium. The maximum magnetic field of 4 T is provided by a superconducting coil. Flexible heat connection is used between the pre-cooler and ADR, so heat generated by vibration decreases. From (3 K, 4 T), the lowest temperature can reach 0.47 K by adiabatic demagnetization, which is consistent with the result drawn from the entropy data. In a constant-temperature-control mode, the demagnetization rate is controlled by a feedback loop, so the temperature can be held in the presence of a load. A cooling capacity of 2.7 J is provided at 1 K, with temperature fluctuation being lower than 0.5 mK, and the second thermodynamic efficiency of adiabatic demagnetization refrigeration is 57%. at 0.8 K, the cooling capacity is 1.2 J.Future work on improving the performance includes the improving of the on-off ratio of the heat switch, so, the irreversible loss caused by the heat transfer temperature difference in conduction state can be reduced. Improving the heat transfer performance of the salt pill, the heat can be ejected in a shorter period.This refrigerating machine is the first Chinese adiabatic demagnetization refrigeration system that can be operated in circulation, which is expected to be the 1^st stage of a three-stage adiabatic demagnetization refrigeration system in a 50 mK temperature zone. This study lays a foundation for further developing continuous multistage adiabatic demagnetization refrigeration at ultra-low temperature.

Keywords:

作者及机构信息

1.
中国科学院理化技术研究所, 低温工程学重点实验室, 北京　100190

2.
中国科学院大学, 北京　100190

3.
中国科学院赣江创新研究院, 赣州　341000

4.
中国科学院物理研究所, 磁学国家重点实验室, 北京　100190

通信作者: 沈俊, jshen@mails.ipc.ac.cn

基金项目: 国家自然科学基金(批准号: 51925605)和中国科学院科研仪器设备研制项目(批准号: GJJSTD20190001)资助的课题

Authors and contacts

1.
Key Laboratory of Cryogenic Engineering, Technical Institute of Physical and Chemistry, Chinese Academy of Sciences, Beijing 100190, China

2.
University of Chinese Academy of Sciences, Beijing 100190, China

3.
Ganjiang Innovation Academy, Chinese Academy of Sciences, Ganzhou 341000, China

4.
State Key Laboratory of Magnetism, Institute of Physics, Chinese Academy of Sciences, Beijing 100190, China

Corresponding author: Shen Jun, jshen@mails.ipc.ac.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant No. 51925605) and the Scientific Instrument Developing Project of the Chinese Academy of Sciences (Grant No. GJJSTD20190001)

文章全文 : translate this paragraph

参考文献

[1]	Collaudin B, Rando N 2000 Cryogenics 40 797 Google Scholar
[2]	Coccia E 2000 Physica B 280 525 Google Scholar
[3]	Osheroff D D, Richardson R C, Lee D M 1972 Phys. Rev. Lett. 29 88 Google Scholar
[4]	Hornibrook J M, Colless J I, Lamb I D C, et al. 2014 Phys. Rev. Appl. 3 024010 Google Scholar
[5]	Pobell F 2006 Matters and Methods at Low Temperature (New York: Acid-free Paper) pp203, 209, 206
[6]	De Haas W J, Wiersma E C, Kramers H A 1933 Physica 1 1 Google Scholar
[7]	Giauque W F, MacDougall D P 1933 Phys. Rev. 43 768
[8]	Kurti N, Simon F 1934 Nature 133 907 Google Scholar
[9]	Shirron P, Canavan E, Dipirro M, Jackson M, King T, Panek J, Tuttle J 2001 Cryogenics 41 789 Google Scholar
[10]	Shirron P J 2014 Cryogenics 62 130 Google Scholar
[11]	万绍宁, 容锡燊 1987 低温 2 133 Google Scholar Wan S N, Rong X S 1987 Chin. J. Low Temp. 2 133 Google Scholar
[12]	Wikus P, Canavan E, Heine S T, et al. 2014 Cryogenics. 62 150 Google Scholar
[13]	Fisher R A, Brodale G E, Hornung E W, Giauque W F 1973 J. Chem. Phys. 59 4652 Google Scholar
[14]	Goshorn D P, Onn D G, Remeika J P 1977 Phys. Rev. B 15 3527 Google Scholar
[15]	Numazawa T, Kamiya K, Shirron P, DiPirro M, Matsumoto K 2006 AIP Conf. Proc. 850 1579 Google Scholar
[16]	Diego A P B, Jean-Maec D, Christophe M, Emmanuelle B, Jean-Pascal B, Mike Z, Nicolas L 2019 Cryogenics 2 105 Google Scholar
[17]	Hagmann C, Benford D J, Richards P L 1994 Cryogenics 34 213 Google Scholar
[18]	王昌, 王亚男, 刘远威, 戴巍, 沈俊 2019 真空与低温 25 317 Google Scholar Wang C, Wang Y N, Liu Y W, Dai W, Shen J 2019 Vacuum & Cryogenics 25 317 Google Scholar
[19]	Daudin B, Lagnier R, Salce B 1982 J. Magn. Magn. Mater. 27 315 Google Scholar
[20]	Model 372 AC Bridge and Temperature Controller, Lakeshore http://www.lakeshore.com/products/product-detail/model-372/[2021-12-30]

施引文献

图 1 ADR的基本构成

Fig. 1. Basic components of ADR.

下载: 全尺寸图片幻灯片

图 2 ADR制冷循环

Fig. 2. Refrigeration cycle of ADR.

下载: 全尺寸图片幻灯片

图 3 制冷系统示意图

Fig. 3. Schematic diagram of refrigeration system.

下载: 全尺寸图片幻灯片

图 4 制冷系统实物图

Fig. 4. Photo of refrigeration system.

下载: 全尺寸图片幻灯片

图 5 ADR的实际循环

Fig. 5. Thermodynamic cycle of ADR.

下载: 全尺寸图片幻灯片

图 6 典型的ADR工作过程

Fig. 6. Typical running process of ADR.

下载: 全尺寸图片幻灯片

图 7 绝热去磁过程中温度-磁场对应关系

Fig. 7. T-B diagram during adiabatic demagnetization progress.

下载: 全尺寸图片幻灯片

表 1 常见亚开温区制冷技术对比

Table 1. Comparison of commonly used sub-Kelvin refrigeration technology.

	原理	适用温区	优点	缺点
DR	氦3从其浓相进入稀相时吸收热量	5 mK—1 K	制冷温度低冷量大可连续制冷	依赖重力依赖稀缺氦3
SR	工质饱和温度和饱和蒸气压的对应关系, 蒸发制冷	300 mK—1 K	结构简单可靠性高	最低温下限较高热效率低依赖稀缺氦3
ADR	磁热材料的磁熵随外加磁场变化	2 mK—1 K	内禀高效不依赖重力工质易得	单级制冷不连续可能有电磁干扰

下载: 导出CSV

表 2 ADR中常用的磁热工质

Table 2. Commonly used magnetocaloric materials (MCM) in ADR.

名称	化学式	最低工作温度/K
GGG^[13]	Gd₃Ga₅O₁₂	0.38
DGG^[14]	Dy₃Ga₅O₁₂	0.6
GLF^[15]	GdLiF₄	0.48
YbGG^[16]	Yb₃Ga₅O₁₂	0.054
MAS^[5]	Mn(SO₄)₂(NH₄)₂·6H₂O	0.17
FAA^[5]	Fe(SO₄)₂(NH₄)₂·12H₂O	0.026
CPA^[5]	CrK(SO₄)₂·12H₂O	0.009
CCA^[17]	CrCs(SO₄)₂·12H₂O	0.01
CMN^[5]	Ce₂Mg₃(NO₃)₁₂·24H₂O	0.0015

下载: 导出CSV

表 3 ADR中常用的热开关^[18]

Table 3. Commonly used heat switches in ADR.

	适用温区	开关比	寄生热来源	优缺点
机械式	不受限制	—	机械能损耗	可完全断开结构复杂、耐用性差
超导式	≤ 0.5 K	> 100	剩余导热涡流产热	温区下限低需额外磁场
气体式	≥ 0.2 K	≈1000	剩余导热	结构简单、可被动驱动较低温区失效
磁阻式	≤ 20 K	> 1000	剩余导热涡流产热	适用温区广、开关比大需额外磁场

下载: 导出CSV

map

[1]	Collaudin B, Rando N 2000 Cryogenics 40 797 Google Scholar
[2]	Coccia E 2000 Physica B 280 525 Google Scholar
[3]	Osheroff D D, Richardson R C, Lee D M 1972 Phys. Rev. Lett. 29 88 Google Scholar
[4]	Hornibrook J M, Colless J I, Lamb I D C, et al. 2014 Phys. Rev. Appl. 3 024010 Google Scholar
[5]	Pobell F 2006 Matters and Methods at Low Temperature (New York: Acid-free Paper) pp203, 209, 206
[6]	De Haas W J, Wiersma E C, Kramers H A 1933 Physica 1 1 Google Scholar
[7]	Giauque W F, MacDougall D P 1933 Phys. Rev. 43 768
[8]	Kurti N, Simon F 1934 Nature 133 907 Google Scholar
[9]	Shirron P, Canavan E, Dipirro M, Jackson M, King T, Panek J, Tuttle J 2001 Cryogenics 41 789 Google Scholar
[10]	Shirron P J 2014 Cryogenics 62 130 Google Scholar
[11]	万绍宁, 容锡燊 1987 低温 2 133 Google Scholar Wan S N, Rong X S 1987 Chin. J. Low Temp. 2 133 Google Scholar
[12]	Wikus P, Canavan E, Heine S T, et al. 2014 Cryogenics. 62 150 Google Scholar
[13]	Fisher R A, Brodale G E, Hornung E W, Giauque W F 1973 J. Chem. Phys. 59 4652 Google Scholar
[14]	Goshorn D P, Onn D G, Remeika J P 1977 Phys. Rev. B 15 3527 Google Scholar
[15]	Numazawa T, Kamiya K, Shirron P, DiPirro M, Matsumoto K 2006 AIP Conf. Proc. 850 1579 Google Scholar
[16]	Diego A P B, Jean-Maec D, Christophe M, Emmanuelle B, Jean-Pascal B, Mike Z, Nicolas L 2019 Cryogenics 2 105 Google Scholar
[17]	Hagmann C, Benford D J, Richards P L 1994 Cryogenics 34 213 Google Scholar
[18]	王昌, 王亚男, 刘远威, 戴巍, 沈俊 2019 真空与低温 25 317 Google Scholar Wang C, Wang Y N, Liu Y W, Dai W, Shen J 2019 Vacuum & Cryogenics 25 317 Google Scholar
[19]	Daudin B, Lagnier R, Salce B 1982 J. Magn. Magn. Mater. 27 315 Google Scholar
[20]	Model 372 AC Bridge and Temperature Controller, Lakeshore http://www.lakeshore.com/products/product-detail/model-372/[2021-12-30]

[1]	孙震, 吕项, 李盛, 安忠. 绝热表象下非绝热分子动力学方法. , 2024, 73(14): 140201. doi: 10.7498/aps.73.20240401
[2]	黄远志, 杨传浩, 何颂平, 马瑞松, 郇庆. 基于干式制冷的低温扫描探针显微镜研究进展. , 2024, 73(22): 228701. doi: 10.7498/aps.73.20241367
[3]	郑茂文, 郭浩文, 卫铃佼, 潘子杰, 邹佳润, 李瑞鑫, 赵密广, 陈厚磊, 梁惊涛. 稀释制冷技术. , 2024, 73(23): 230701. doi: 10.7498/aps.73.20241211
[4]	俎红叶, 程维军, 王亚男, 王晓涛, 李珂, 戴巍. 冷凝泵型稀释制冷机实验研究. , 2023, 72(8): 080701. doi: 10.7498/aps.72.20222257
[5]	李珂, 王亚男, 刘萍, 禹芳秋, 戴巍, 沈俊. 50 mK多级绝热去磁制冷机的实验研究. , 2023, 72(19): 190702. doi: 10.7498/aps.72.20231102
[6]	宋志军, 吕昭征, 董全, 冯军雅, 姬忠庆, 金勇, 吕力. 极低温散粒噪声测试系统及隧道结噪声测量. , 2019, 68(7): 070702. doi: 10.7498/aps.68.20190114
[7]	杨巨涛, 李清亮, 王建国, 郝书吉, 潘威炎. 双频双波束加热电离层激发甚低频/极低频辐射理论分析. , 2017, 66(1): 019401. doi: 10.7498/aps.66.019401
[8]	刘式达, 付遵涛, 刘式适. 从北极高压、南极低压到南北极间的三维异宿轨道. , 2014, 63(21): 214701. doi: 10.7498/aps.63.214701
[9]	郝书吉, 李清亮, 杨巨涛, 吴振森. 电离层调制加热产生极低频/甚低频波定向辐射的理论分析. , 2013, 62(22): 229402. doi: 10.7498/aps.62.229402
[10]	姚洪斌, 郑雨军. NaI分子的非绝热效应. , 2011, 60(12): 128201. doi: 10.7498/aps.60.128201
[11]	张毅. Birkhoff系统的一类新型绝热不变量. , 2006, 55(8): 3833-3837. doi: 10.7498/aps.55.3833
[12]	闫冰, 潘守甫, 王志刚, 于俊华. S3解离中的非绝热过程. , 2006, 55(4): 1736-1739. doi: 10.7498/aps.55.1736
[13]	沈建其, 庄　飞. 螺旋光纤系统中非绝热条件几何相移. , 2005, 54(3): 1048-1052. doi: 10.7498/aps.54.1048
[14]	孟继宝, 陈兆甲, 雒建林, 白海洋, 汪卫华, 郑萍, 张杰, 苏少奎, 王玉鹏. 重费密子系统CeCu6-xNix的极低温电阻研究. , 2001, 50(8): 1632-1636. doi: 10.7498/aps.50.1632
[15]	袁进胜, 孙昌璞. 旋转样品核四极共振的量子绝热微扰论分析. , 1995, 44(1): 29-34. doi: 10.7498/aps.44.29
[16]	陈学俊, 王岩, 曹小平. 反散射理论导出极低能量下的e-He相互作用势. , 1994, 43(9): 1427-1432. doi: 10.7498/aps.43.1427
[17]	蒋祺, 沈顺清, 陶瑞宝. 两个量子窄区串联时的绝热输运和欧姆输运. , 1993, 42(7): 1157-1161. doi: 10.7498/aps.42.1157
[18]	蒋祺；沈顺清；陶瑞宝. 两个量子窄区串联时的绝热输运和欧姆输运. , 1991, 40(7): 1157-1161. doi: 10.7498/aps.40.1157
[19]	高智, 卢文强. 非平衡、非绝热气体中的波. , 1983, 32(6): 713-722. doi: 10.7498/aps.32.713
[20]	周洁, 王占国, 刘志刚, 王万年, 尤兴凯. 硅的低温电学性质. , 1966, 22(4): 404-411. doi: 10.7498/aps.22.404

计量

文章访问数: 8540
PDF下载量: 236
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板