-
基于一维弹道导体, 建立了三端纳米线制冷机模型. 该模型是由一个中间空腔和左右电子库组成, 中间空腔和两电子库通过一维纳米线导体进行连接. 利用朗道方程和基本热力学公式推导出两电子库之间电荷流和能量流的表达式, 进而得出该制冷机模型的工作区间, 然后分析其性能特征并讨论制冷机性能优化. 研究表明: 不同的参数下该制冷机会有不同的制冷区间, 但每个制冷区间都存在一个温差上限, 超过该温差, 此装置将不能进行制冷. 制冷率随制冷系数变化的特征曲线为回原点扭叶型曲线, 这为衡量该制冷机性能提供了重要指标. 尽可能减小纳米线的能级宽度会提高该制冷机的工作性能.In this paper, the model of a three-terminal nanowire refrigerator is established based on one-dimensional (1D) ballistic conductor. It is composed of an intermediate cavity and left/right electron reservoir in which the intermediate cavity and left/right electron reservoir are connected by 1D nanowire conductor. The expression for the charge current and that for the energy current flowing from two electron reservoirs are derived by using Landauer formula and basic thermodynamic laws. Then, the working region of the refrigerator is obtained, its performance characteristics are analyzed, and its performance optimization is discussed. It is shown that the refrigerator under different parameters operates in different working regions. For each refrigeration region, there is an upper limit of temperature difference, and the refrigerator will be unable to refrigerate beyond the upper limit. The characteristic curve of the cooling rate changing with performance coefficient is a loop-shaped one, which provides an important index for us to evaluate the performance of the refrigerator. The energy level width of the nanowire can be reduced as much as possible, which will improve the performance of the refrigerator.
-
Keywords:
- three-terminal thermoelectric refrigerator /
- nanowires /
- cooling rate /
- coefficient of performance
[1] Hicks L D, Dresselhaus M S 1993 Phys. Rev. B 47 12727
Google Scholar
[2] Hicks L D, Harman T C, Dresselhaus M S 1993 Appl. Phys. Lett. 63 3230
Google Scholar
[3] Venkatasubramanian R, Siivola E, Colpittes T, O’Quinn B 2001 Nature 413 597
Google Scholar
[4] Harman T C, Taylor P J, Walsh M P, LaForge B E 2002 Science 297 2229
Google Scholar
[5] Boukai A I, Bunimovich J, Tahir-Kheli J, Yu J K, Goddard Iii W A, Heath J R 2008 Nature 451 168
Google Scholar
[6] Björk M T, Ohlsson B J, Thelander C, Persson A I, Deppert K, Wallenberg L R, Samuelson L 2002 Appl. Phys. Lett. 81 4458
Google Scholar
[7] Staring A A M, Molenkamp L W, Alphenaar B W, Van Houten H, Buyk O J A, Mabesoone M A A, Beenakker C W J, Foxon C T 1993 Europhys. Lett. 22 57
Google Scholar
[8] Molenkamp L, Staring A A M, Alphenaar B W, Van Houten H, Beenakker C W J 1994 Semicond. Sci. Technol. 9 903
Google Scholar
[9] Dzurak A S, Smith C G, Barnes C H W, Pepper M, Martín-Moreno L, Liang C T, Ritchie D A, Jones G A C 1997 Phys. Rev. B 55 R10197
Google Scholar
[10] Esposito M, Lindenberg K, Van den Broeck C 2009 Europhys. Lett. 85 60010
Google Scholar
[11] Esposito M, Kawai R, Lindenberg K, Van den Broeck C 2010 Phys. Rev. E 81 041106
Google Scholar
[12] Esposito M, Kumar N, Lindenberg K, Van den Broeck C 2012 Phys. Rev. E 85 031117
Google Scholar
[13] Su S H, Zhang Y C, Peng W L, Su G Z, Chen J C 2021 Sci. Sin. Phys. 51 030011
[14] Su G Z, Zhang Y C, Cai L, Su S H, Chen J C 2015 Energy 90 1842
Google Scholar
[15] Su G Z, Liao T J, Chen L W, Chen J C 2016 Energy 101 421
Google Scholar
[16] Su G Z, Pan Y Z, Zhang Y C, Shih T M, Chen J C 2016 Energy 113 723
Google Scholar
[17] Peng W L, Liao T J, Zhang Y C, Su G Z, Lin G X, Chen J C 2017 Energy Convers. Manage. 143 391
Google Scholar
[18] Peng W L, Zhang Y C, Yang Z M, Chen J C 2018 Eur. Phys. J. Plus. 133 38
Google Scholar
[19] Peng W L, Ye Z L, Zhang X, Chen J C 2018 Energy Convers. Manage. 166 74
Google Scholar
[20] Edwards H L, Niu Q, De Lozanne A L 1993 Appl. Phys. Lett. 63 1815
Google Scholar
[21] Edwards H L, Niu Q, Georgakis G A, De Lozanne A L 1995 Phys. Rev. B 52 5714
[22] Prance J R, Smith C G, Griffiths J P, Chorley S J, Anderson D, Jones G A C, Farrer I, Ritchie D A 2009 Phys. Rev. Lett. 102 146602
Google Scholar
[23] Jiang J H, Entin-Wohlman O, Imry Y 2012 Phys. Rev. B 85 075412
Google Scholar
[24] Jiang J H 2014 J. Appl. Phys. 116 194303
Google Scholar
[25] Jiang J H, Imry Y 2018 Phys. Rev. B 97 125422
Google Scholar
[26] Jordan A N, Sothmann B, Sánchez R, Büttiker M 2013 Phys. Rev. B 87 075312
Google Scholar
[27] Qiu S S, Ding Z M, Chen L G, Meng F K, Sun F R 2019 The Euro. Phys. J. Plus. 134 273
Google Scholar
[28] Ding Z M, Chen L G, Ge Y L, Xie Z H 2019 Sci. China: Tech. Sci. 62 397
Google Scholar
[29] Li W, Yang Y Y, Fu J, He J Z 2020 ES. Energy Environment 7 40
[30] Lin Z B, Li W, Fu J, Yang Y Y, He J Z 2019 Chin. Phys. Lett. 36 060501
Google Scholar
[31] Lin Z B, Li W, Yang Y Y, He J Z 2020 Phys. Rev. B 101 022117
[32] Su H, Shi Z C, He J Z 2015 Chin. Phys. Lett. 32 100501
Google Scholar
[33] Fu J, Li W, Shi Z C, He J Z 2018 Chin. J. Phys. 56 895
Google Scholar
[34] Shi Z C, He J Z, Xiao Y L 2015 Sci. Sin. Phys. 45 050502
[35] Shi Z C, Qin W F, He J Z 2016 Mod. Phys. Lett. B 30 1650397
Google Scholar
[36] Yang Y Y, Xu S, Li W, He J Z 2020 Phys. Scr. 95 095001
Google Scholar
[37] Yang Y Y, Xu S, He J Z 2020 Chin. Phys. Lett. 37 120502
Google Scholar
[38] Thierschmann H, Sánchez R, Sothmann B, Arnold F, Heyn C, Hansen W, Buhmann H, Molenkamp L W 2015 Nature Nanotechnology 10 854
Google Scholar
[39] Roche B, Roulleau P, Julien T, Jompol Y, Farrer I, Ritchie D A, Glattli D C 2015 Nature Commun. 6 6738
Google Scholar
[40] Hartmann F, Pfeffer P, Hofling S, Kamp M, Worschech L 2015 Phys. Rev. Lett. 114 146805
Google Scholar
[41] Jaliel G, Puddy R K, Sánchez R, Jordan A N, Sothmann B, Farrer I, Griffiths J P, Ritchie D A, Smith C G 2019 Phys. Rev. Lett. 123 117701
Google Scholar
[42] Hochbaum A I, Chen R, Delgado R D, Liang W, Garnett E C, Najarian M, Majumdar, Yang P 2008 Nature 451 163
Google Scholar
[43] Björk M T, Ohlsson B J, Sass T, Thelander C, Persson A I, Magnusson M H, Deppert K, Wallenberg L R, Samuelson L 2020 Appl. Phys. Lett. 80 1058
[44] Datta S 1995 Electronic Transport in Mesoscopic Systems (Cambridge: Cambridge University Press)
[45] Nakpathomkun N, Xu H Q, Linke H 2010 Phys. Rev. B 82 235428
Google Scholar
-
图 1 (a) 三端纳米线制冷机模型图; (b) 传输函数
${\tau _i}\left( E \right)$ 作为能量${E_i}$ 的函数Fig. 1. (a) The schematic diagram of a three-terminal nanowire refrigerator; (b) transmission function
${\tau _i}\left( E \right)$ as a function of energy level${E_i}$ .
图 2 (a) 在
$\gamma \to 0$ 的情况下制冷机的工作区间; (b) 当γ取不同的值时对工作区间的影响Fig. 2. (a) The working region of the refrigerator in the case of
$\gamma \to 0$ ; (b) the working regions at given different value γ
图 3 在
$\gamma \to 0$ 时(a)制冷率和(b)制冷系数随着能级位置变化的三维图; (c)—(f)分别是$\gamma = 0.5$ 和$\gamma = 1$ 对应的制冷率和制冷系数的三维图Fig. 3. Three-dimensional graphs for (a) the cooling rate and (b) the coefficient of performance varying with the energy level positions under
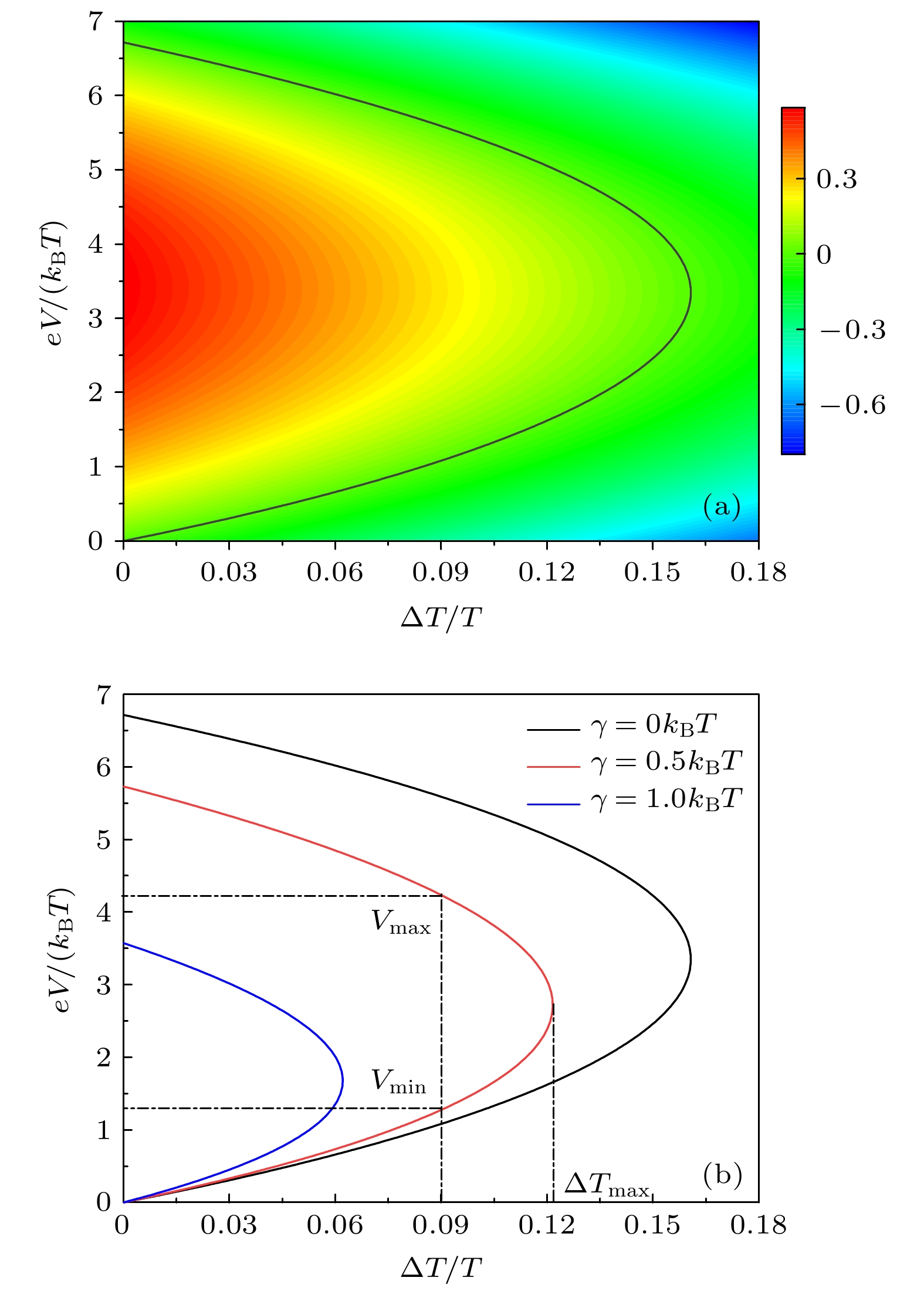
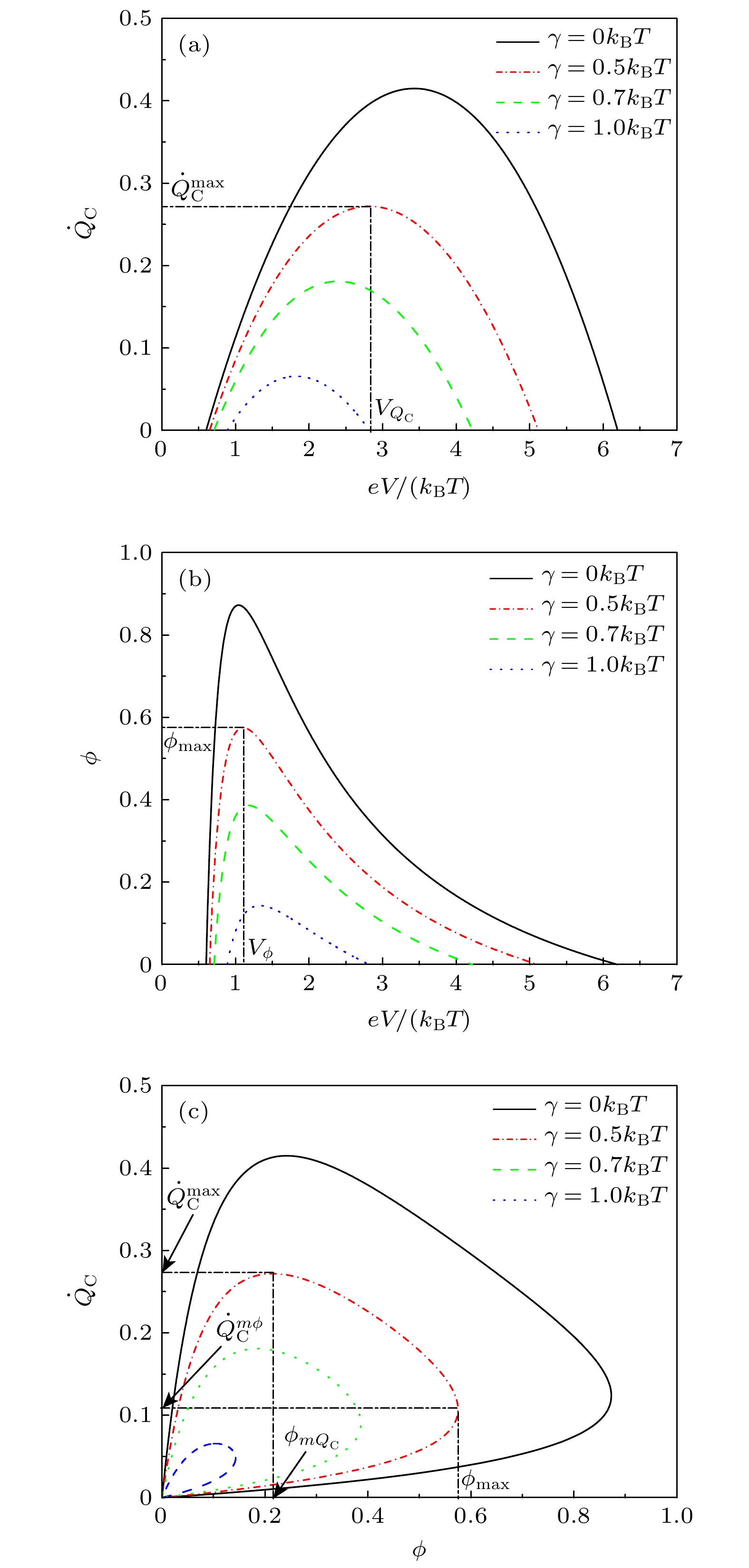
$\gamma \to 0$ ; (c)–(f) are the three-dimensional graphs for the cooling rate and the coefficient of performance at given$\gamma = 0.5$ and$\gamma = 1$ , respectively.
图 4 (a) 制冷率关于电压的函数图像; (b) 制冷系数关于电压的函数图像; (c) 制冷机的
${\dot{{Q}}_{\text{C}}}{-}\varphi$ 特征图Fig. 4. (a) The cooling rate as a function of voltage; (b) the coefficient of performance as a function of voltage; (c) the characteristic curves of
${\dot{{Q}}_{\text{C}}}{-}\varphi$ at given different value γ.
图 5 (a) 优化的制冷率随电压变化的图像; (b) 相应制冷系数随电压变化的图像; (c) 最优能级位置随电压变化的图像
Fig. 5. (a) The curves of the optimized cooling rate as a function of voltage; (b) the curves of the corresponding coefficient of performance as a function of voltage; (c) the curves of the optimal energy level position as a function of voltage.
图 6 (a) 优化的制冷率随能级宽度变化的图像; (b) 相应的制冷系数随能级宽度变化的图像; (c) 最优能级位置随能级宽度变化的图像
Fig. 6. (a) The curves of the optimized cooling rate as a function of the width of energy level; (b) the curves of the corresponding coefficient of performance as a function of the width of energy level; (c) the curves of the optimal position of energy level as a function of the width of energy level.
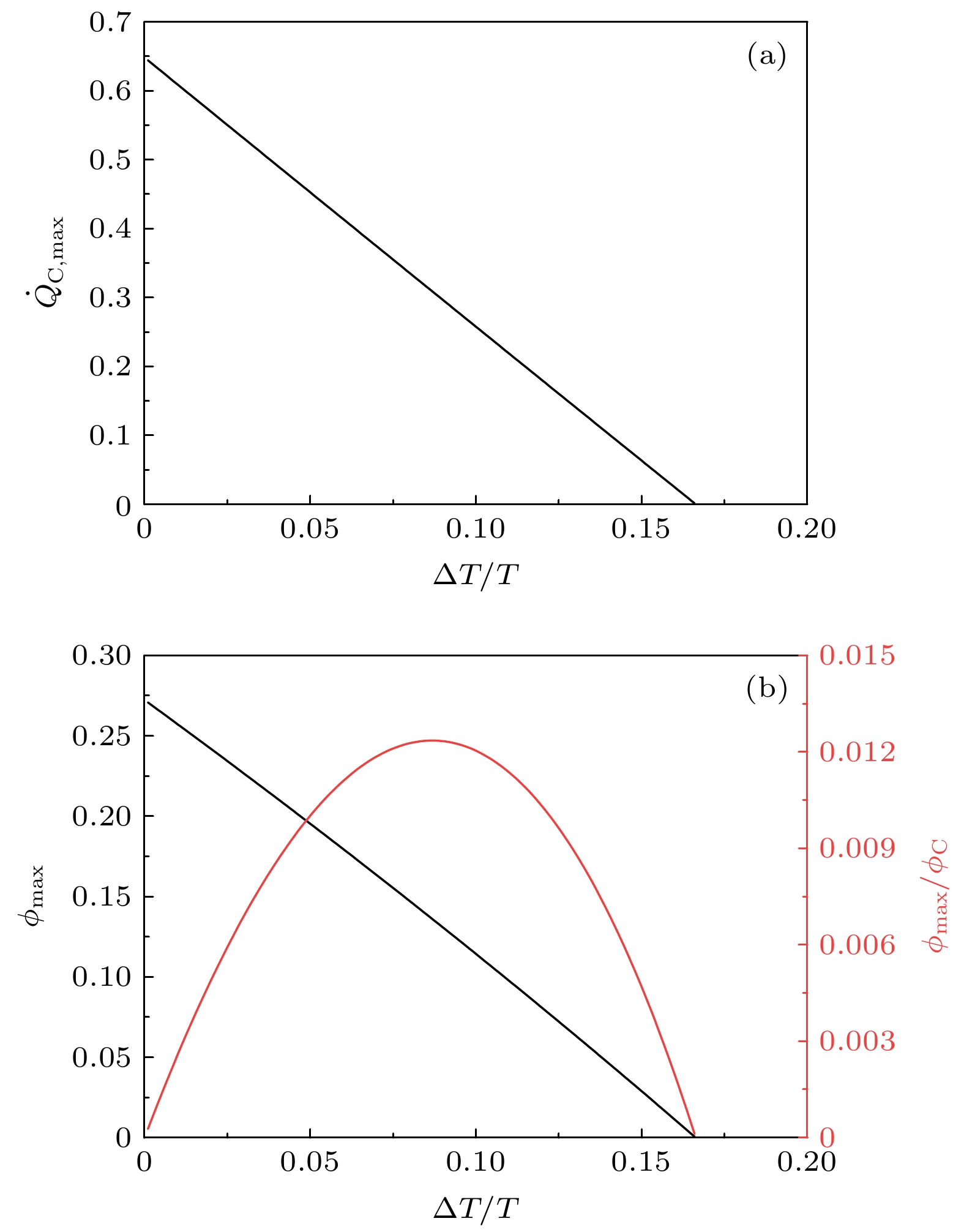
图 7 (a) 最大制冷率随温差变化的图像; (b) 最大制冷率下的制冷系数和以卡诺制冷系数为单位的制冷系数随温差变化的图像
Fig. 7. (a) The curves of the maximum cooling rate as a function of the temperature difference; (b) the curves of the coefficient of performance at the maximum cooling rate and the coefficient of performance in a unit of Carnot value as a function of the temperature difference.
-
[1] Hicks L D, Dresselhaus M S 1993 Phys. Rev. B 47 12727
Google Scholar
[2] Hicks L D, Harman T C, Dresselhaus M S 1993 Appl. Phys. Lett. 63 3230
Google Scholar
[3] Venkatasubramanian R, Siivola E, Colpittes T, O’Quinn B 2001 Nature 413 597
Google Scholar
[4] Harman T C, Taylor P J, Walsh M P, LaForge B E 2002 Science 297 2229
Google Scholar
[5] Boukai A I, Bunimovich J, Tahir-Kheli J, Yu J K, Goddard Iii W A, Heath J R 2008 Nature 451 168
Google Scholar
[6] Björk M T, Ohlsson B J, Thelander C, Persson A I, Deppert K, Wallenberg L R, Samuelson L 2002 Appl. Phys. Lett. 81 4458
Google Scholar
[7] Staring A A M, Molenkamp L W, Alphenaar B W, Van Houten H, Buyk O J A, Mabesoone M A A, Beenakker C W J, Foxon C T 1993 Europhys. Lett. 22 57
Google Scholar
[8] Molenkamp L, Staring A A M, Alphenaar B W, Van Houten H, Beenakker C W J 1994 Semicond. Sci. Technol. 9 903
Google Scholar
[9] Dzurak A S, Smith C G, Barnes C H W, Pepper M, Martín-Moreno L, Liang C T, Ritchie D A, Jones G A C 1997 Phys. Rev. B 55 R10197
Google Scholar
[10] Esposito M, Lindenberg K, Van den Broeck C 2009 Europhys. Lett. 85 60010
Google Scholar
[11] Esposito M, Kawai R, Lindenberg K, Van den Broeck C 2010 Phys. Rev. E 81 041106
Google Scholar
[12] Esposito M, Kumar N, Lindenberg K, Van den Broeck C 2012 Phys. Rev. E 85 031117
Google Scholar
[13] Su S H, Zhang Y C, Peng W L, Su G Z, Chen J C 2021 Sci. Sin. Phys. 51 030011
[14] Su G Z, Zhang Y C, Cai L, Su S H, Chen J C 2015 Energy 90 1842
Google Scholar
[15] Su G Z, Liao T J, Chen L W, Chen J C 2016 Energy 101 421
Google Scholar
[16] Su G Z, Pan Y Z, Zhang Y C, Shih T M, Chen J C 2016 Energy 113 723
Google Scholar
[17] Peng W L, Liao T J, Zhang Y C, Su G Z, Lin G X, Chen J C 2017 Energy Convers. Manage. 143 391
Google Scholar
[18] Peng W L, Zhang Y C, Yang Z M, Chen J C 2018 Eur. Phys. J. Plus. 133 38
Google Scholar
[19] Peng W L, Ye Z L, Zhang X, Chen J C 2018 Energy Convers. Manage. 166 74
Google Scholar
[20] Edwards H L, Niu Q, De Lozanne A L 1993 Appl. Phys. Lett. 63 1815
Google Scholar
[21] Edwards H L, Niu Q, Georgakis G A, De Lozanne A L 1995 Phys. Rev. B 52 5714
[22] Prance J R, Smith C G, Griffiths J P, Chorley S J, Anderson D, Jones G A C, Farrer I, Ritchie D A 2009 Phys. Rev. Lett. 102 146602
Google Scholar
[23] Jiang J H, Entin-Wohlman O, Imry Y 2012 Phys. Rev. B 85 075412
Google Scholar
[24] Jiang J H 2014 J. Appl. Phys. 116 194303
Google Scholar
[25] Jiang J H, Imry Y 2018 Phys. Rev. B 97 125422
Google Scholar
[26] Jordan A N, Sothmann B, Sánchez R, Büttiker M 2013 Phys. Rev. B 87 075312
Google Scholar
[27] Qiu S S, Ding Z M, Chen L G, Meng F K, Sun F R 2019 The Euro. Phys. J. Plus. 134 273
Google Scholar
[28] Ding Z M, Chen L G, Ge Y L, Xie Z H 2019 Sci. China: Tech. Sci. 62 397
Google Scholar
[29] Li W, Yang Y Y, Fu J, He J Z 2020 ES. Energy Environment 7 40
[30] Lin Z B, Li W, Fu J, Yang Y Y, He J Z 2019 Chin. Phys. Lett. 36 060501
Google Scholar
[31] Lin Z B, Li W, Yang Y Y, He J Z 2020 Phys. Rev. B 101 022117
[32] Su H, Shi Z C, He J Z 2015 Chin. Phys. Lett. 32 100501
Google Scholar
[33] Fu J, Li W, Shi Z C, He J Z 2018 Chin. J. Phys. 56 895
Google Scholar
[34] Shi Z C, He J Z, Xiao Y L 2015 Sci. Sin. Phys. 45 050502
[35] Shi Z C, Qin W F, He J Z 2016 Mod. Phys. Lett. B 30 1650397
Google Scholar
[36] Yang Y Y, Xu S, Li W, He J Z 2020 Phys. Scr. 95 095001
Google Scholar
[37] Yang Y Y, Xu S, He J Z 2020 Chin. Phys. Lett. 37 120502
Google Scholar
[38] Thierschmann H, Sánchez R, Sothmann B, Arnold F, Heyn C, Hansen W, Buhmann H, Molenkamp L W 2015 Nature Nanotechnology 10 854
Google Scholar
[39] Roche B, Roulleau P, Julien T, Jompol Y, Farrer I, Ritchie D A, Glattli D C 2015 Nature Commun. 6 6738
Google Scholar
[40] Hartmann F, Pfeffer P, Hofling S, Kamp M, Worschech L 2015 Phys. Rev. Lett. 114 146805
Google Scholar
[41] Jaliel G, Puddy R K, Sánchez R, Jordan A N, Sothmann B, Farrer I, Griffiths J P, Ritchie D A, Smith C G 2019 Phys. Rev. Lett. 123 117701
Google Scholar
[42] Hochbaum A I, Chen R, Delgado R D, Liang W, Garnett E C, Najarian M, Majumdar, Yang P 2008 Nature 451 163
Google Scholar
[43] Björk M T, Ohlsson B J, Sass T, Thelander C, Persson A I, Magnusson M H, Deppert K, Wallenberg L R, Samuelson L 2020 Appl. Phys. Lett. 80 1058
[44] Datta S 1995 Electronic Transport in Mesoscopic Systems (Cambridge: Cambridge University Press)
[45] Nakpathomkun N, Xu H Q, Linke H 2010 Phys. Rev. B 82 235428
Google Scholar
下载:
计量
- 文章访问数: 3585
- PDF下载量: 46
- 被引次数: 0
