-
When white light laser is focused on liquids, colorful interference rings with different shapes, i.e. “coherent rainbows” can be seen. The formation mechanism of such coherent rainbows is described as follows. The laser heating changes the local temperature distribution of the liquid, which affects the refractive index locally and thus the optical path difference, i.e. thermal lens effect which may cause the laser to go off at large angles. The curvature of the laser wavefront and the convection and bubbles in the liquid can also play some roles as reported here. The wave front curvature results in the asymmetry of the coherent rainbows in the near of the focal point because the wave front curvature in front of the focal point is negative and the wave front curvature in the rear of the focal point is positive. The coherent rainbow has an oval shape with up-down asymmetry because convection in the locally heated liquid leads to an asymmetric temperature distribution. We construct a function including wave front curvature and thermal lens effect, and obtain the relationship between the size of the coherent rainbows and the position of the sample. As a result of the liquid instability induced by the laser heating, the temperature distribution in the liquid is no longer axisymmetric, thus, the focal length of the transverse and longitudinal thermal concave lens are no longer the same. The fitting results accord well with the experimental observations that the coherent rainbows change faster (slower) in front of (rear) the focal point and the longitudinal and transverse dimension of the coherent rainbow are different. Many tiny bubbles are generated in water in the center of the laser beam, forming a local “black barrier” which explains the observation that there are diffraction rings and Poisson-type bright spots in the dark area of the coherent rainbows. The coherent rainbows can be observed in many liquids where the shape and number of rings of coherent rainbows depend on liquid properties such as density, viscosity and thermal conductivity.
-
Keywords:
- coherent interference /
- diffraction /
- bubble /
- Poisson bright spot
[1] Zolot’ko A S, Kitaeva V F, Kroo N, Sobolev N, Chillag L 1980 JETP Lett. 32 158
[2] He K X, Abeleldayem H, Sekhar P C, Venkateswarlu P, George M C 1991 Opt. Commun. 81 101
Google Scholar
[3] Pilla V, Munin E, Gesualdi M R R 2009 J. Opt. A: Pure Appl. Opt. 11 105201
Google Scholar
[4] Wang W H, Wu Y L, Wu Q, Hua J J, Zhao J M 2016 Sci. Rep. 6 22072
Google Scholar
[5] Wang X, Yan Y F, Cheng H, Wang Y H, Han J B 2018 Mater. Lett. 214 247
Google Scholar
[6] Hu L L, Sun F, Zhao H, Zhao J M 2019 Opt. Lett. 44 5214
Google Scholar
[7] Jiang Y Q, Ma Y, Fan Z Y, Wang P, Li X H, Wang Y W, Zhang Y, Shen J Q, Wang G, Yang Z J, Xiao S, Gao Y, He J 2018 Opt. Lett. 43 523
Google Scholar
[8] Shi B X, Miao L L, Wang Q K, Du J, Tang P H, Liu J, Zhao C J, Wen S C 2015 Appl. Phys. Lett. 107 151101
Google Scholar
[9] Jia Y, Liao Y L, Wu L M, Shan Y X, Dai X Y, Cai H Z, Xiang Y J, Fan D Y 2019 Nanoscale 11 4515
Google Scholar
[10] Wang Y N, Tang Y J, Cheng P H, Zhou X F, Zhu Z, Liu Z P, Liu D, Wang Z M, Bao J M 2017 Nanoscale 9 3547
Google Scholar
[11] Wu Y L, Wu Q, Sun F, Cheng C, Meng S, Zhao J M 2015 Proc. Natl. Acad. Sci. USA 112 11800
Google Scholar
[12] Wu L M, Xie Z J, Zhao J L, Wang Y Z, Jiang X T, Ge Y Q, Zhang F, Lu S B, Guo Z N, Liu J, Xiang Y J, Xu S X, Li J Q, Fan D Y, Zhang H 2018 Adv. Opt. Mater. 6 1700985
Google Scholar
[13] Zhang Q, Cheng X M, He B, Ren Z Y, Zhang Y, Chen H W, Bai J T 2018 Opt. Laser Technol. 102 140
Google Scholar
[14] Yao J J, Cheng X M, Zhang Q, Tang X J, Chen H W, Bai J 2019 J. Phys. Chem. Lett. 10 6213
Google Scholar
[15] 孙天娇, 尚雅轩, 钱轩, 姬扬 2018 67 034205
Google Scholar
Sun T J, Shang Y X, Qian X, Ji Y 2018 Acta. Phys. Sin. 67 034205
Google Scholar
[16] Sun T J, Qian X, Shang Y X, Liu J, Wang K Y, Ji Y 2018 Sci. Bull. 63 531
Google Scholar
[17] 孙天娇, 钱轩, 尚雅轩, 刘剑, 王开友, 姬扬 2018 67 184204
Google Scholar
Sun T J, Qian X, Shang Y X, Liu J, Wang K Y, Ji Y 2018 Acta. Phys. Sin. 67 184204
Google Scholar
[18] Shi T T, Qian X, Sun T J, Cheng L, Dou R J, Liu L Y, Ji Y 2021 Chin. Phys. B 30 124208
Google Scholar
[19] 沃尔夫冈∙戴姆特瑞德 著 (姬扬 译) 2012 激光光谱学(第I卷): 基础理论 (北京: 科学出版社) 第338—341页
Wolfgang Demtroder (translated by Ji Y) 2012 Laser Spectroscopy (Volume I): Basic Theory (Beijing: Science Press) pp338–341 (in Chinese)
[20] Zhang Q H, Qiu Y, Lin F, Niu C, Zhou X F, Liu Z P, Alam M K, Dai S Y, Zhang W, Hu J T, Wand Z M, Bao J M 2020 Nanoscale 12 7190
Google Scholar
-
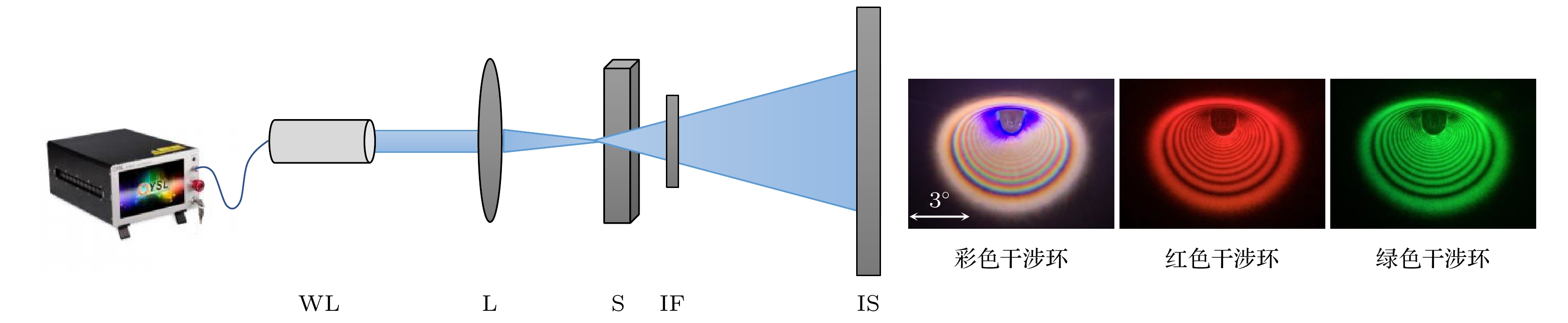
图 1 实验装置示意图. 白光脉冲光纤激光器(WL)经透镜聚焦(L)照射在液体样品(S)上, 在成像屏(IS)上形成彩色干涉环. 在样品后方放置干涉滤光片(IF), 在成像屏(IS)上形成单色干涉环. 干涉滤光片(IF)的中心波长分别为632.8 nm (红色)和532 nm (绿色), 半带宽为10 nm ± 2 nm
Figure 1. Schematics of the experimental set-up. The white laser (WL) beam from a pulsed fiber laser is focused through a lens (L) into a liquid sample (S), and colorful interference rings (coherent rainbows) appear on the image screen (IS). With an interference filter (IF) inserted behind the sample, monochromatic interference rings appear on the image screen. The center wavelength of the interference filter (IF) are 632.8 nm (red) and 532 nm (green), respectively. The half bandwidth is 10 nm ± 2 nm.
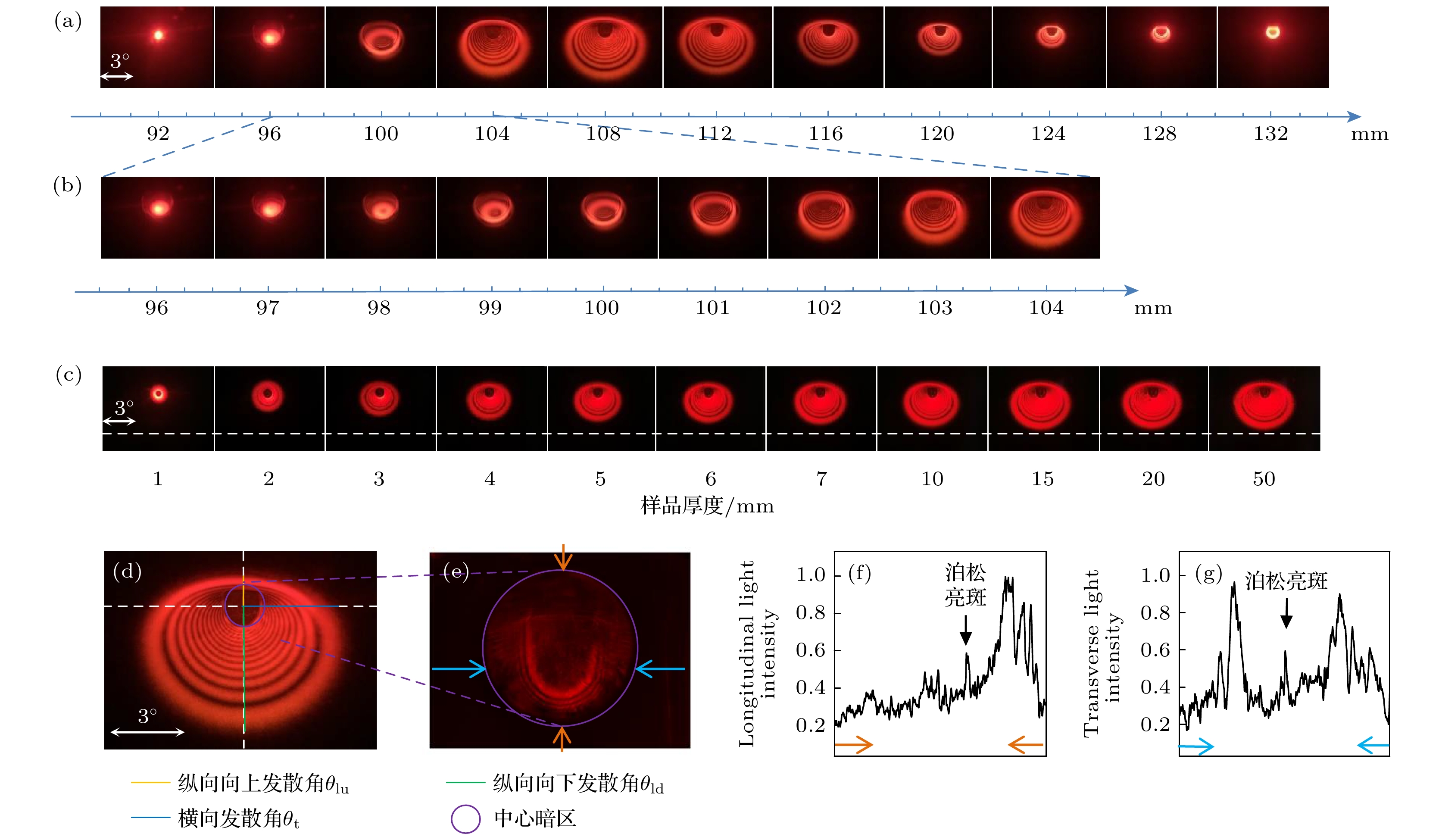
图 2 干涉环的形状依赖于样品的位置和厚度(包括中心暗区的细节) (a) 改变样品前端面到凸透镜(焦距为100 mm)的距离(92—132 mm, 每次移动4 mm), 尺寸最大的干涉环出现在样品离透镜108 mm时, 以此时的样品位置为基准, 其右侧位置(样品远离凸透镜)的干涉环变小的速度比左侧慢; (b) 在焦点左侧, 样品在不同位置(96—104 mm, 每次移动1 mm)形成的干涉环; (c) 固定样品前端面的位置与凸透镜的距离(d = 108 mm), 改变样品的厚度, 干涉环的形状和尺寸都会发生变化; (d)干涉图案左右对称, 只有一个横向发散角
$ {\theta _{\rm t}} $ ; 上下不对称, 向上发散角$ {\theta }_{\mathrm{l}\mathrm{u}} $ 小于向下发散角$ {\theta }_{\mathrm{l}\mathrm{d}} $ ; 干涉环有一个中心暗区, 放大后(e)可以看到一些内疏外密的衍射环和泊松亮斑; (f), (g)中心暗区的纵向(横向)光强分布图, 分别对应于图(e)中用橙色(蓝色)箭头标示的直线区域, 黑色箭头给出了泊松亮斑的位置.Figure 2. Shape of the interference rings depends on the position and the thickness of the sample (including details of the dark area in the center): (a) Vary the position of the sample from the lens (from 92 mm to 132 mm, with a step of 4 mm), the interference rings reach their maximum size when the sample position is at 108 mm from the lens. Moving the sample to the right side (being farther away from the lens), the interference rings become smaller and smaller, however, the size-change rate is slower than that in the case of moving the sample to the left side. (b) Similar to panel (a), but the sample is now moved from 96 mm to 104 mm with a step of 1 mm. (c) Increase the thickness of the sample but leave its position unmoved (d = 108 mm), the shape and size of the interference rings also change. (d) The interference pattern has the left-right symmetry, as indicated by the transverse divergence angle
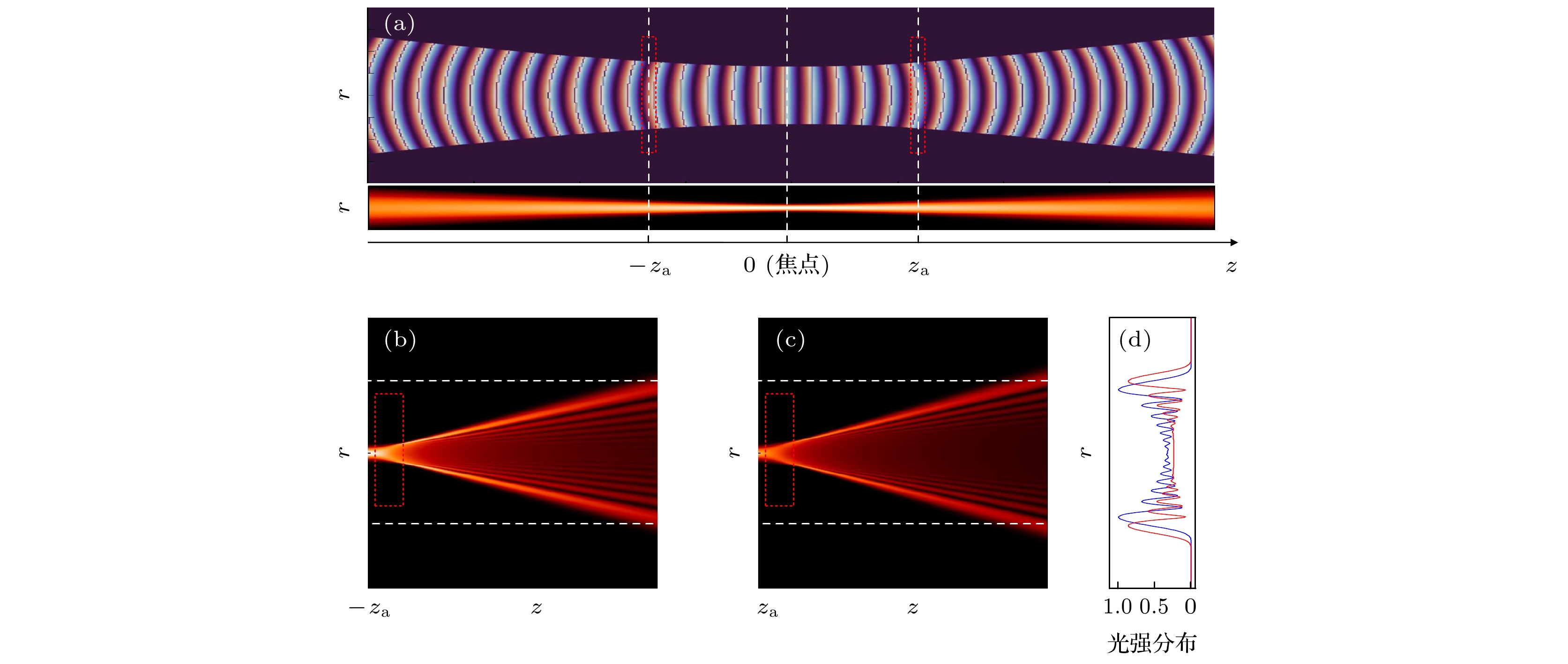
${\theta _{\rm t}}$ ; it has not the up-down symmetry, and the longitudinal “up” divergence angle$ {\theta }_{\mathrm{l}\mathrm{u}} $ is much smaller than the longitudinal “down” divergence angle$ {\theta }_{\mathrm{l}\mathrm{d}} $ ; in the center is a dark area, the enlarged view of which shows (e) diffraction rings that are sparse inside and dense outside and Poisson-type bright spot. (f), (g) Light intensity distribution in the dark area along the longitudinal (transverse) direction, corresponding to the line indicated by the orange (blue) arrow in panel (e).
图 3 在焦点左右相同位置相干彩虹不对称的定性分析 (a) 在焦点附近波阵面和光强分布示意图; (b) 样品位于焦点前(
$ {-z}_{\mathrm{a}} $ )的干涉环模拟图; (c) 样品位于焦点后($ {z}_{\mathrm{a}} $ )的干涉环模拟图, 在焦距前后相同距离, 焦点后的干涉环尺寸大于焦点前(白色虚线), 红色虚线框是装有液体样品的比色皿; (d) 样品位于焦点前${-z}_{\mathrm{a}}$ (蓝色曲线)和焦点后$ {z}_{\mathrm{a}} $ (红色曲线), 干涉环的纵向光强分布图Figure 3. Qualitative analysis of the asymmetry of the coherent rainbows when the sample is located at the same distance on the left and right of the focus: (a) Schematics of the wavefront and the light intensity distribution of a Gaussian beam around the focal point. (b), (c) Simulation pattern of the interference rings with the sample being located in the incident plane
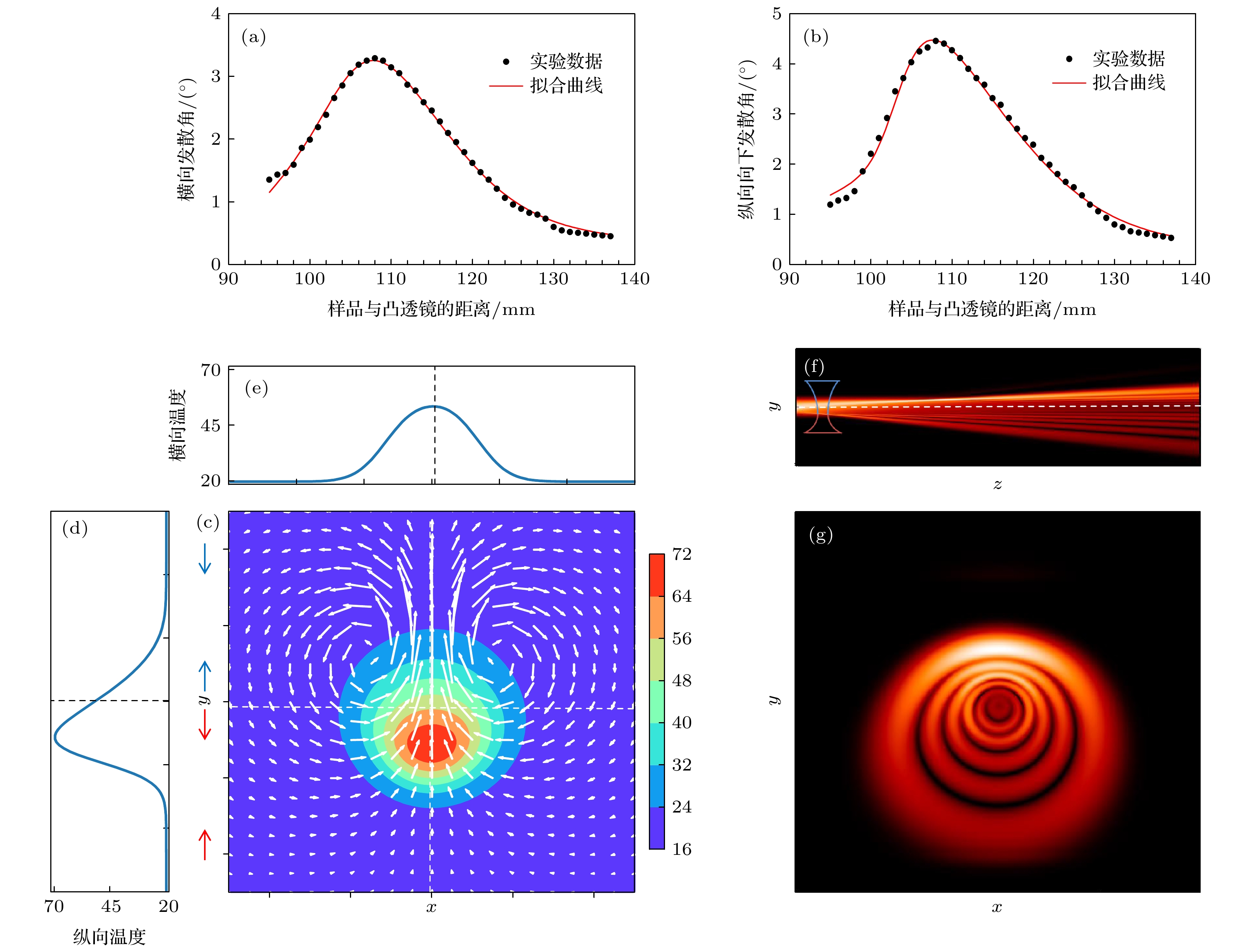
$ -{z}_{\mathrm{a}} $ ($ {z}_{\mathrm{a}} $ ) on the left (right) side of the focal point. The size of the interference rings with the sample on the right side is larger than that on the left side, as indicated by the white dash lines. The red dotted frame shows the cuvette which contains the liquid sample. (d) The longitudinal light intensity distribution of the interference rings of the sample on the left side (blue curve) and right side (red curve) of the focal point.
图 4 不对称相干彩虹的形成机制(构建一个包含波前曲率和热透镜效应的函数, 通过参数拟合得到干涉环尺寸随样品位置的关系) (a)样品距离凸透镜不同位置, 干涉环横向发散角
$ {\theta }_{\mathrm{l}\mathrm{t}} $ 的实验数据和拟合曲线; (b) 样品距离凸透镜不同位置, 干涉环纵向发散角$ {\theta }_{\mathrm{l}\mathrm{d}} $ 的实验数据和拟合曲线; (c) 液体中的温度分布和液体对流图; (d) 液体纵向温度分布曲线, 液体纵向上半部分温度梯度(蓝色箭头对应区域)小于纵向下半部分温度梯度(红色箭头对应区域), 从而产生了上小下大的不对称干涉环; (e) 液体横向温度分布曲线; (f) 在平面yoz的干涉环模拟图; (g) 在平面xoy的干涉环模拟图Figure 4. Mechanism behind the dependence of the coherent rainbows on the sample position. A function including wavefront curvature and thermal lens effect is constructed. The relationship between the size of the interference rings and the position of the sample is obtained by parameter fitting. (a), (b) The experimental data and fitting results of the transverse “up” divergence angle
$ {\theta }_{\mathrm{l}\mathrm{u}} $ (the longitudinal “down” divergence angle$ {\theta }_{\mathrm{l}\mathrm{d}} $ ) vs. sample position d relative to the lens; (c) temperature distribution in the liquid sample and the convection diagram; (d), (e) longitudinal (transverse) temperature distribution in the liquid, note that the temperature gradient in the upper half of the liquid is smaller than that in the lower half, resulting in up-down asymmetry of the interference rings; (f), (g) simulation diagram of interference rings in plane yoz ( plane xoy).
图 5 衍射图案和泊松亮斑依赖于气泡和激光束的相对位置. 由于激光光轴中心能量密度最大, 因此在光路中心生成了大量气泡. 将这些气泡的整体轮廓等效为一个边缘粗糙的气泡. (a)—(c)位于光轴中心位置的单个光滑气泡(左)以及相应的干涉图案(中)和纵向光强分布图(右); (d)—(f)位于光轴中心位置的粗糙气泡(左)以及相应的干涉图案(中)和纵向光强分布图(右); (g)—(i)位于光轴中心偏上位置的粗糙气泡(左)以及相应的干涉图案(中)和纵向光强分布图(右)
Figure 5. Diffraction pattern and the Poisson-type bright spot depend on the relative position of the bubbles and the laser beam. Due to the maximum energy density in the center of the laser beam, a large number of bubbles are generated in the center of the optical path. The overall contour of these bubbles is equivalent to a bubble with rough edges. (a)–(c) A “smooth” bubble is located at the center of the optical axis (left panel), together with its interference pattern (central panel) and light distribution along the longitudinal direction (right panel); (d)–(f) a “smooth” bubble is located at above the center of the optical axis (left panel), together with its interference pattern (central panel) and light distribution along the longitudinal direction (right panel); (g)–(i) a “rough” bubble is located at above the center of the optical axis (left panel), together with its interference pattern (central panel) and light distribution along the longitudinal direction (right panel)
-
[1] Zolot’ko A S, Kitaeva V F, Kroo N, Sobolev N, Chillag L 1980 JETP Lett. 32 158
[2] He K X, Abeleldayem H, Sekhar P C, Venkateswarlu P, George M C 1991 Opt. Commun. 81 101
Google Scholar
[3] Pilla V, Munin E, Gesualdi M R R 2009 J. Opt. A: Pure Appl. Opt. 11 105201
Google Scholar
[4] Wang W H, Wu Y L, Wu Q, Hua J J, Zhao J M 2016 Sci. Rep. 6 22072
Google Scholar
[5] Wang X, Yan Y F, Cheng H, Wang Y H, Han J B 2018 Mater. Lett. 214 247
Google Scholar
[6] Hu L L, Sun F, Zhao H, Zhao J M 2019 Opt. Lett. 44 5214
Google Scholar
[7] Jiang Y Q, Ma Y, Fan Z Y, Wang P, Li X H, Wang Y W, Zhang Y, Shen J Q, Wang G, Yang Z J, Xiao S, Gao Y, He J 2018 Opt. Lett. 43 523
Google Scholar
[8] Shi B X, Miao L L, Wang Q K, Du J, Tang P H, Liu J, Zhao C J, Wen S C 2015 Appl. Phys. Lett. 107 151101
Google Scholar
[9] Jia Y, Liao Y L, Wu L M, Shan Y X, Dai X Y, Cai H Z, Xiang Y J, Fan D Y 2019 Nanoscale 11 4515
Google Scholar
[10] Wang Y N, Tang Y J, Cheng P H, Zhou X F, Zhu Z, Liu Z P, Liu D, Wang Z M, Bao J M 2017 Nanoscale 9 3547
Google Scholar
[11] Wu Y L, Wu Q, Sun F, Cheng C, Meng S, Zhao J M 2015 Proc. Natl. Acad. Sci. USA 112 11800
Google Scholar
[12] Wu L M, Xie Z J, Zhao J L, Wang Y Z, Jiang X T, Ge Y Q, Zhang F, Lu S B, Guo Z N, Liu J, Xiang Y J, Xu S X, Li J Q, Fan D Y, Zhang H 2018 Adv. Opt. Mater. 6 1700985
Google Scholar
[13] Zhang Q, Cheng X M, He B, Ren Z Y, Zhang Y, Chen H W, Bai J T 2018 Opt. Laser Technol. 102 140
Google Scholar
[14] Yao J J, Cheng X M, Zhang Q, Tang X J, Chen H W, Bai J 2019 J. Phys. Chem. Lett. 10 6213
Google Scholar
[15] 孙天娇, 尚雅轩, 钱轩, 姬扬 2018 67 034205
Google Scholar
Sun T J, Shang Y X, Qian X, Ji Y 2018 Acta. Phys. Sin. 67 034205
Google Scholar
[16] Sun T J, Qian X, Shang Y X, Liu J, Wang K Y, Ji Y 2018 Sci. Bull. 63 531
Google Scholar
[17] 孙天娇, 钱轩, 尚雅轩, 刘剑, 王开友, 姬扬 2018 67 184204
Google Scholar
Sun T J, Qian X, Shang Y X, Liu J, Wang K Y, Ji Y 2018 Acta. Phys. Sin. 67 184204
Google Scholar
[18] Shi T T, Qian X, Sun T J, Cheng L, Dou R J, Liu L Y, Ji Y 2021 Chin. Phys. B 30 124208
Google Scholar
[19] 沃尔夫冈∙戴姆特瑞德 著 (姬扬 译) 2012 激光光谱学(第I卷): 基础理论 (北京: 科学出版社) 第338—341页
Wolfgang Demtroder (translated by Ji Y) 2012 Laser Spectroscopy (Volume I): Basic Theory (Beijing: Science Press) pp338–341 (in Chinese)
[20] Zhang Q H, Qiu Y, Lin F, Niu C, Zhou X F, Liu Z P, Alam M K, Dai S Y, Zhang W, Hu J T, Wand Z M, Bao J M 2020 Nanoscale 12 7190
Google Scholar
-
154202-20220455补充材料.pdf
154202-20220455-video-1.MOV
DownLoad:
Catalog
Metrics
- Abstract views: 4259
- PDF Downloads: 72
- Cited By: 0
