-
We introduce two contactless measurement methods at extremely low temperature: capacitances and surface acoustic waves. Both methods can be used to study the physical properties of the quantum system through the interaction between electrons and high frequency electric field. We first present preliminary results of high-mobility two-dimensional electron systems studied by a high-precision capacitance measurement method at extremely low temperature. Our setup can resolve < 0.05% variation of a < 1 pF capacitance at 10 mK–300 K and 0–14 T. Second, we also study two-dimensional electron systems using surface acoustic waves. We can use 0.1 nW excitation and obtain < 10–5 sensitivity. These measurement methods may be widely applied to the study of two-dimensional systems, especially the materials without high quality contacts.
-
Keywords:
- two-dimensional electron systems /
- quantum hall effect /
- capacitance /
- surface acoustic wave
[1] Chen Y, Lewis R M, Engel L W, Tsui D C, Ye P D, Pfeiffer L N, West K W 2003 Phys. Rev. Lett. 91 016801
Google Scholar
[2] Zudov M A, Du R R, Simmons J A, Reno J L 2001 Phys. Rev. B 64 201311
Google Scholar
[3] Ashoori R C, Stormer H L, Weiner J S, Pfeiffer L N, Pearton S J, Baldwin K W, West K W 1992 Phys. Rev. Lett. 68 3088
Google Scholar
[4] Kaplit M, Zemel J N 1968 Phys. Rev. Lett. 21 212
Google Scholar
[5] Voshchenkov A M, Zemel J N 1974 Phys. Rev. B 9 4410
[6] Smith T P, Goldberg B B, Stiles P J, Heiblum M 1985 Phys. Rev. B 32 2696
[7] Mosser V, Weiss D, Klitzing K, Ploog K, Weimann G 1986 Solid State Commun. 58 5
Google Scholar
[8] Smith T P, Wang W I, Stiles P J 1986 Phys. Rev. B 34 2995
Google Scholar
[9] Yang M J, Yang C H, Bennett B R, Shanabrook B V 1997 Phys. Rev. Lett. 78 4613
Google Scholar
[10] Eisenstein J P, Pfeiffer L N, West K W 1994 Phys. Rev. B 50 1760
Google Scholar
[11] Zibrov A A, Kometter C, Zhou H, Spanton E M, Taniguchi T, Watanabe K, Zaletel M P, Young A F 2017 Nature 549 360
Google Scholar
[12] Irie H, Akiho T, Muraki K 2019 Appl. Phys. Express 12 063004
Google Scholar
[13] Eisenstein J P, Pfeiffer L N, West K W 1992 Phys. Rev. Lett. 68 674
Google Scholar
[14] Deng H, Pfeiffer L N, West K W, Baldwin K W, Engel L W, Shayegan M 2019 Phys. Rev. Lett. 122 116601
Google Scholar
[15] Jo J, Garcia E A, Abkemeier K M, Santos M B, Shayegan M 1993 Phys. Rev. B 47 4056
Google Scholar
[16] Zibrov A A, Rao P, Kometter C, et al. 2018 Phys. Rev. Lett. 121 167601
Google Scholar
[17] Tomarken S L, Cao Y, Demir A, et al. 2019 Phys. Rev. Lett. 123 046601
Google Scholar
[18] Zhao L, Lin W, Fan X, Song Y, Lu H, Liu Y 2022 Rev. Sci. Instrum. 93 053910
[19] Zhao L, Lin W, Chung Y J, Baldwin K W, Pfeiffer L N, Liu Y 2022 arXiv: 2201.06203 [cond-mat.mes-hall]
[20] Verbiest G J, Janssen H, Xu D 2019 Rev. Sci. Instrum. 90 084706
Google Scholar
[21] Willett R L, Paalanen M A, Ruel R R, West K W, Pfeiffer L N, Bishop D J 1990 Phys. Rev. Lett. 65 112
Google Scholar
[22] Friess B, Peng Y, Rosenow B, von Oppen F, Umansky V, von Klitzing K, Smet J H 2017 Nat. Phys. 13 1124
Google Scholar
-
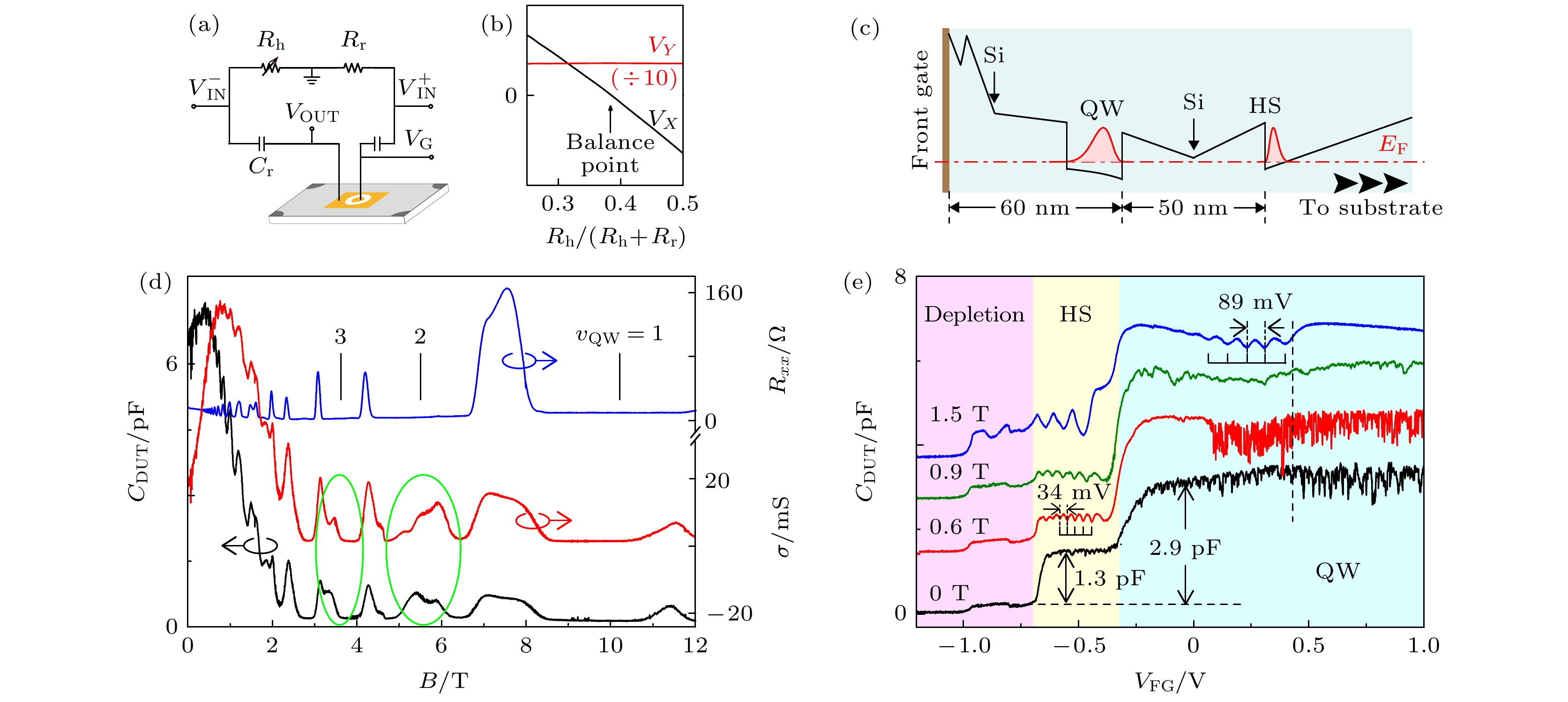
图 1 利用电容测量研究二维电子系统 (a) 测量使用的无源电桥和待测样品结构示意图; (b) 电桥输出随电阻臂电阻比例的变化; (c) 测量中使用的GaAs/AlGaAs异质结样品结构, 样品中包含两层二维电子气, 分别位于量子阱(QW)和缓冲层的异质结界面(HS)处; (d) 常规输运得到的纵向电阻
$R_{xx}$ (蓝色)、由电容测量方法得到的电容$C_{\text{DUT}}$ (黑色)和电导$\sigma$ (红色)随磁场变化的曲线; (e) 电容随顶栅栅压$V_{\text{FG}}$ 的变化展示了多平台结构, 分别对应于耗尽状态、异质结填充和量子阱填充的状态Figure 1. Studying the high-mobility two-dimensional electron gas via capacitance measurement: (a) Schematic diagram of passive bridge and sample geometry. (b) The bridge output varies with the resistance ratio of the resistance arm. (c) The GaAs/AlGaAs heterostructure. The sample contains two layers of two-dimensional electron gas, which locate at the heterojunction interface (HS) of the buffer layer and the quantum well (QW), respectively. (d) The longitudinal resistance
$R_{xx}$ (blue) obtained by conventional transport measurement, the capacitance$C_{\text{DUT}}$ (black) and the conductance$\sigma$ (red) obtained by capacitance measurement. (e) The capacitance versus the top gate voltage$V_{\text{FG}}$ shows multi-plateau corresponding to the state of depletion, heterojunction filling and quantum well filling, respectively
图 2 表面声波原理及测量结果 (a) 测量的样品结构, 通过湿法刻蚀去除叉指电极附近的二维电子气, 刻蚀深度足够浅而不会影响表面声波传播; (b) 利用光学方法测量得到的表面声波电极和表面声波强度分布; (c) 在17 mK测量得到的表面声波器件的幅频以及相频特性, 利用相频特性曲线斜率可以得到测量延迟并推导出声波波速约2800 m/s; (d) 表面声波测量得到的声波幅度和声速随磁场的变化. 在强磁场中, 当二维电子气出现量子霍尔效应时声波幅度增加, 波速会加快
Figure 2. SAW measurement setup and results: (a) The sample structure. We remove the two-dimensional electron gas near the cross-finger electrodes by wet etching. The etching depth is shallow enough without affecting SAW propagation. (b) SAW intensity distribution measured by optical method. (c) Amplitude and phase of device measured at 17 mK. The SAW velocity is about 2800 m/s deduced from the slope of the phase vs. frequency dependence. (d) The amplitude and velocity of SAW measured with the magnetic field. At high magnetic field, the amplitude and the velocity of SAW increase when the quantum Hall effect occurs in the two-dimensional electron gas
-
[1] Chen Y, Lewis R M, Engel L W, Tsui D C, Ye P D, Pfeiffer L N, West K W 2003 Phys. Rev. Lett. 91 016801
Google Scholar
[2] Zudov M A, Du R R, Simmons J A, Reno J L 2001 Phys. Rev. B 64 201311
Google Scholar
[3] Ashoori R C, Stormer H L, Weiner J S, Pfeiffer L N, Pearton S J, Baldwin K W, West K W 1992 Phys. Rev. Lett. 68 3088
Google Scholar
[4] Kaplit M, Zemel J N 1968 Phys. Rev. Lett. 21 212
Google Scholar
[5] Voshchenkov A M, Zemel J N 1974 Phys. Rev. B 9 4410
[6] Smith T P, Goldberg B B, Stiles P J, Heiblum M 1985 Phys. Rev. B 32 2696
[7] Mosser V, Weiss D, Klitzing K, Ploog K, Weimann G 1986 Solid State Commun. 58 5
Google Scholar
[8] Smith T P, Wang W I, Stiles P J 1986 Phys. Rev. B 34 2995
Google Scholar
[9] Yang M J, Yang C H, Bennett B R, Shanabrook B V 1997 Phys. Rev. Lett. 78 4613
Google Scholar
[10] Eisenstein J P, Pfeiffer L N, West K W 1994 Phys. Rev. B 50 1760
Google Scholar
[11] Zibrov A A, Kometter C, Zhou H, Spanton E M, Taniguchi T, Watanabe K, Zaletel M P, Young A F 2017 Nature 549 360
Google Scholar
[12] Irie H, Akiho T, Muraki K 2019 Appl. Phys. Express 12 063004
Google Scholar
[13] Eisenstein J P, Pfeiffer L N, West K W 1992 Phys. Rev. Lett. 68 674
Google Scholar
[14] Deng H, Pfeiffer L N, West K W, Baldwin K W, Engel L W, Shayegan M 2019 Phys. Rev. Lett. 122 116601
Google Scholar
[15] Jo J, Garcia E A, Abkemeier K M, Santos M B, Shayegan M 1993 Phys. Rev. B 47 4056
Google Scholar
[16] Zibrov A A, Rao P, Kometter C, et al. 2018 Phys. Rev. Lett. 121 167601
Google Scholar
[17] Tomarken S L, Cao Y, Demir A, et al. 2019 Phys. Rev. Lett. 123 046601
Google Scholar
[18] Zhao L, Lin W, Fan X, Song Y, Lu H, Liu Y 2022 Rev. Sci. Instrum. 93 053910
[19] Zhao L, Lin W, Chung Y J, Baldwin K W, Pfeiffer L N, Liu Y 2022 arXiv: 2201.06203 [cond-mat.mes-hall]
[20] Verbiest G J, Janssen H, Xu D 2019 Rev. Sci. Instrum. 90 084706
Google Scholar
[21] Willett R L, Paalanen M A, Ruel R R, West K W, Pfeiffer L N, Bishop D J 1990 Phys. Rev. Lett. 65 112
Google Scholar
[22] Friess B, Peng Y, Rosenow B, von Oppen F, Umansky V, von Klitzing K, Smet J H 2017 Nat. Phys. 13 1124
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 3719
- PDF Downloads: 168
- Cited By: 0
