-
For the spreading of thin and free film of a partially wetting liquid with insoluble surfactant under the influence of surface acoustic wave, the dimensionless evolution equations governing the spreading dynamics are derived. The evolution equations contain the film thickness and the surface concentration of insoluble surfactant. Assuming that the thickness of the thin film is much smaller than the wavelength of sound in the liquid, the sound leaking off the surface acoustic wave cannot be sustained in the liquid film, and the acoustic radiation pressure and attenuation of the acoustic wave in the solid are both weak. Then the films spreading under different physical mechanisms are observed by numerical simulation. The results show that the surface acoustic wave drives the liquid film to spread and move. When the capillary stress is weak and the liquid film spreading is mainly controlled by the drift induced by surface acoustic wave, the spreading process consists of rapid spreading stage and balancing stage, and the Marangoni effect caused by uneven distribution of surfactant makes the liquid film spread faster in the first stage. When the capillary stress and the drift jointly dominate film spreading, the spreading process contains three stages, i.e. spreading stage, contracting stage and balancing stage. The effect of surfactant accelerates the spreading process, but the existence of contracting stage makes it take longer for the film to reach equilibrium. In addition, the disjoining pressure used in this paper promotes the liquid film spreading, as well as the Marangoni effect. As the correlation coefficient between disjoining pressure and surfactant concentration, α, and the Marangoni number, M, increase, the maximum thickness and the spreading radius of liquid film change faster.
-
Keywords:
- surface acoustic wave /
- surfactant /
- spreading /
- thin partially wetting liquid film
[1] Bar-Cohen A, Arik M, Ohadi M 2006 Proc. IEEE 94 1549
Google Scholar
[2] Lee K S, Ivanova N, Starov V M, Hilal N, Dutschk V 2008 Adv. Colloid Interf. 144 54
Google Scholar
[3] Afsar-Siddiqui A B, Luckham P F, Matar O K 2003 Adv. Colloid Interf. 106 183
Google Scholar
[4] Brabcova Z, McHale G, Wells G G, Brown C V, Newton M I 2017 Appl. Phys. Lett. 110 121603
Google Scholar
[5] Wang Z, Varma V B, Wang Z P, Ramanujan R V 2015 J. Micromech. Microeng. 25 124001
Google Scholar
[6] Rezk A, Manor O, Yeo L Y, Friend J R 2014 Proc. R. Soc. A 470 20130765
Google Scholar
[7] Rezk A R, Manor O, Friend J R, Yeo L Y 2012 Nat. Commun. 3 1167
Google Scholar
[8] Altshuler G, Manor O 2015 Phys. Fluids 27 102103
Google Scholar
[9] Altshuler G, Manor O 2016 Phys. Fluids 28 72102
Google Scholar
[10] Manor O, Dentry M, Friend J R, Yeo L Y 2011 Soft Matter 7 7976
Google Scholar
[11] Manor O, Rezk A R, Friend J R, Yeo L Y 2015 Phys. Rev. E 91 53015
Google Scholar
[12] Collins D J, Manor O, Winkler A, Schmidt H, Friend J R, Yeo L Y 2012 Phys. Rev. E 86 56312
Google Scholar
[13] Qi A, Yeo L Y, Friend J R 2008 Phys. Fluids 20 74103
Google Scholar
[14] Warner M R E, Craster R V, Matar O K 2002 Phys. Fluids 14 1642
Google Scholar
[15] Schwartz L W, Roy R V 1999 J. Colloid Interface Sci. 218 309
Google Scholar
[16] Manev E D, Pugh R J 1991 Langmuir 7 2253
Google Scholar
[17] Bhakta A, Ruckenstein E 1997 Adv. Colloid Interf. 70 1
Google Scholar
[18] Incropera F P, Lavine A S, Bergman T L, DeWitt D P 2007 Fundamentals of Heat and Mass Transfer (6 ed.) (New York: John Wiley & Sons) p883
[19] Schwartz L W, Roy R V 2003 J. Colloid Interf. Sci. 264 237
Google Scholar
[20] Morozov M, Manor O 2017 J. Fluid Mech. 810 307
Google Scholar
[21] Riley N 1998 Theoret. Comput. Fluid Dyn. 10 349
Google Scholar
[22] Tiberg F, Cazabat A 1994 Langmuir 10 2301
Google Scholar
[23] Birch W R, Knewtson M A, Garoff S, Suter R M 1995 Langmuir 11 48
Google Scholar
[24] Dean D S, Sentenac D 1997 Europhys. Lett. 38 645
Google Scholar
[25] Hayduk W, Laudie H 1974 AIChE J. 20 611
Google Scholar
[26] Hu G, Xu A, Xu Z, Zhou Z 2008 Phys. Fluids 20 102101
Google Scholar
[27] 刘邱祖, 寇子明, 韩振南, 高贵军 2013 62 234701
Google Scholar
Liu Q Z, Kou Z M, Han Z N, Gao G J 2013 Acta Phys. Sin. 62 234701
Google Scholar
-
图 1 放置在SAW器件上的含活性剂薄水膜示意图 (a)俯视图; (b)正视图
Figure 1. Schematic diagram of thin water film with surfactant on a SAW device: (a) Top view; (b) front view.
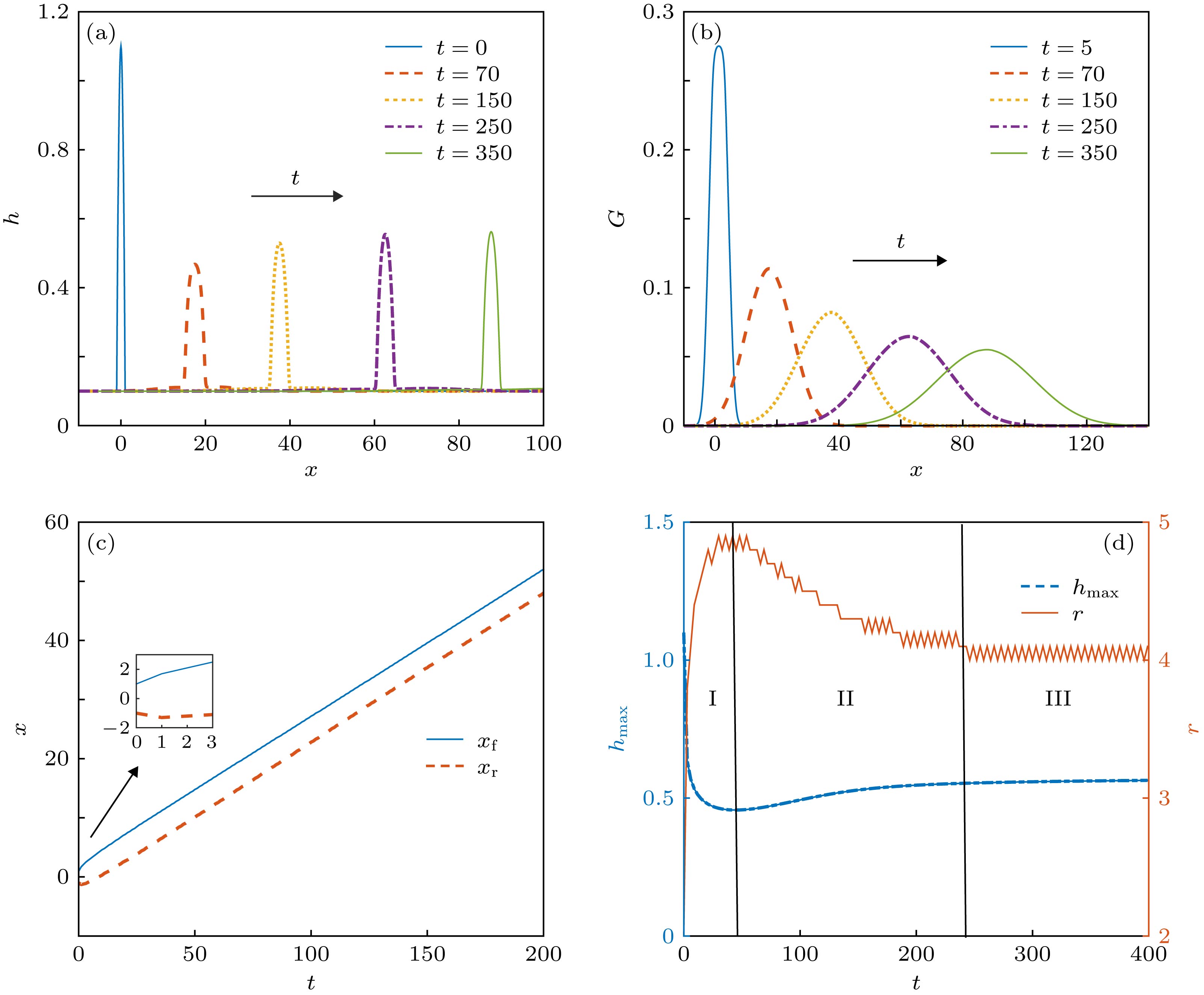
图 2 漂移流起主导作用, 考虑活性剂影响时水膜的铺展过程 (a)液膜厚度; (b)活性剂浓度; (c)液膜前缘xf与后缘xr; (d)最大厚度与铺展半径
Figure 2. Spreading process when the drift of mass governs the film dynamics: (a) Film thickness; (b) surfactant concentration; (c) the position of the front xf and the rear xr of the liquid film; (d) maximal thickness and spreading radius of the liquid film.
图 3 不同时刻下液膜内部的流线与水平方向分速度 (a) t = 10; (b) t = 100
Figure 3. Horizontal velocity contour within the film along with streamlines at different time: (a) t = 10; (b) t = 100.
图 4 漂移流主导时, 考虑活性剂影响和不考虑活性剂影响的液膜演化过程对比
Figure 4. Film profiles at different times during the drift governed spreading process with (blue line) and without (orange line) considering the effect of surfactant.
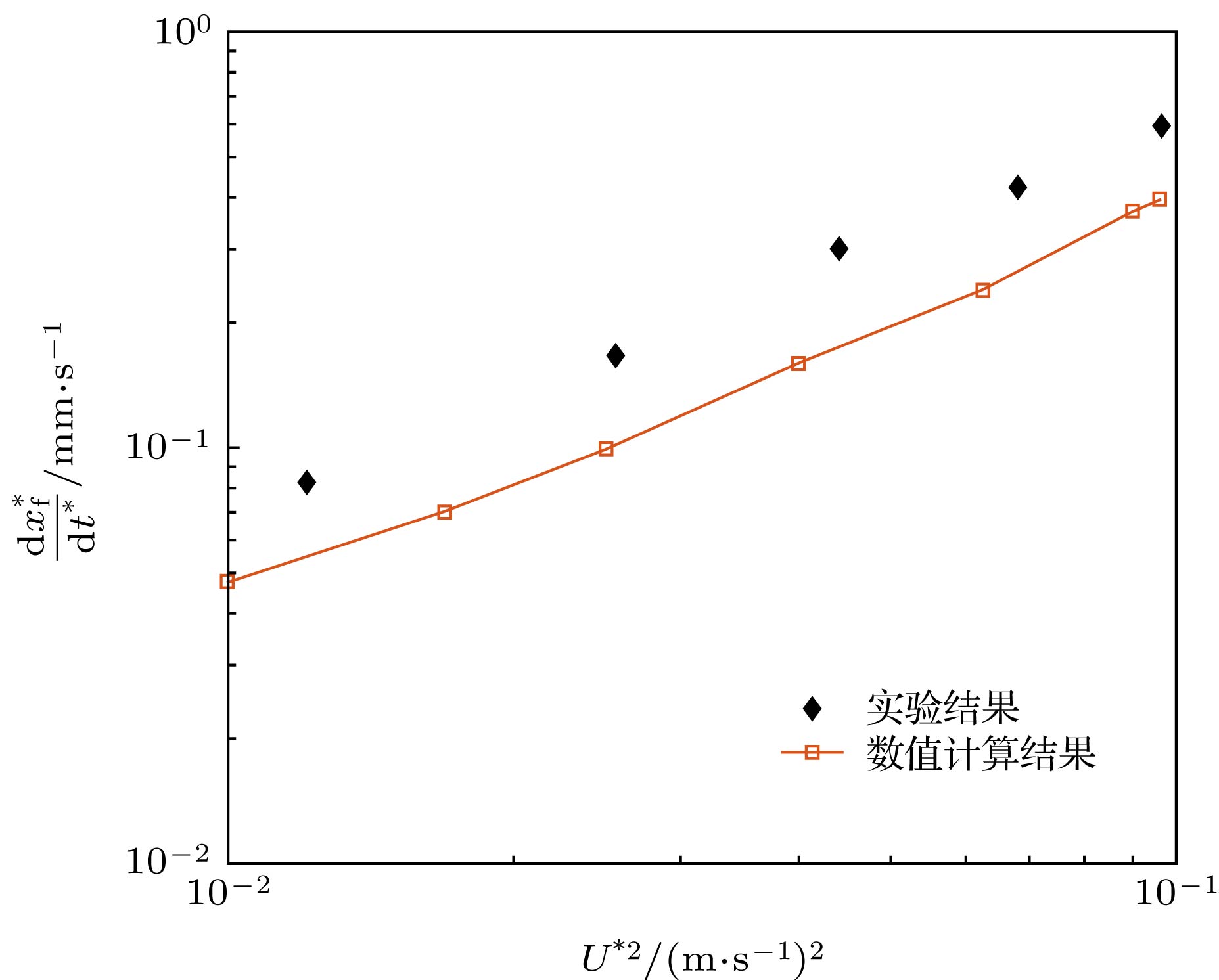
图 5 漂移流主导时, 幂指数n随时间t*的变化与Rezk等[6]的实验结果的对比(液膜前缘位置与时间满足规律xf*～t*n)
Figure 5. Comparison between simulated and experimental[6] results for the variation of exponent n with dimensional time during the drift governed spreading process (the variation of the position of the front of the film with time accords to the power laws xf*～t*n).
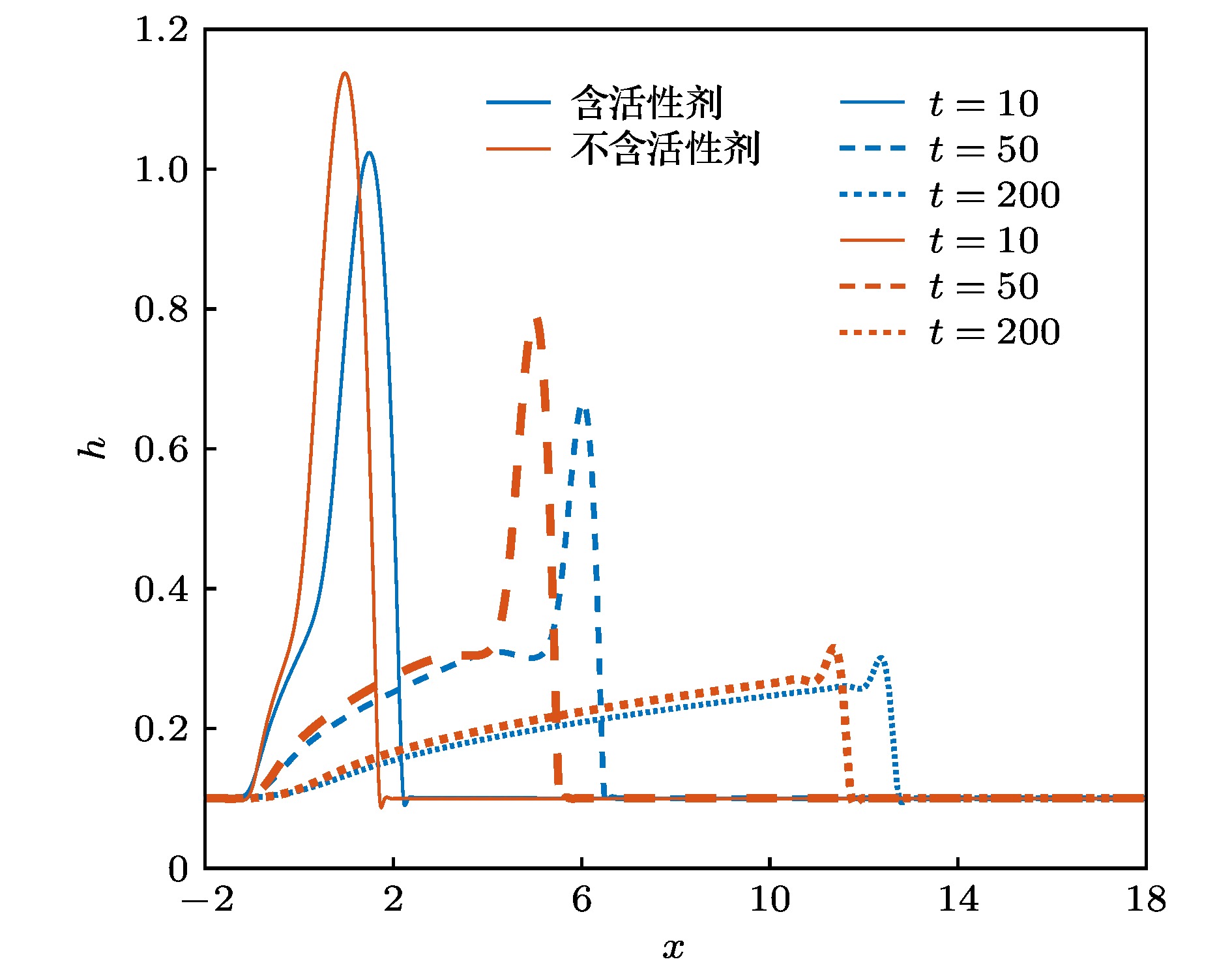
图 7 毛细力和漂移流作用相当, 考虑活性剂影响时水膜的铺展过程 (a)液膜厚度; (b)活性剂浓度; (c)液膜前缘xf与后缘xr; (d)液膜最大厚度hmax与铺展半径r
Figure 7. Spreading process when the equal effect of drift and the capillary stress is considered: (a) Film thickness; (b) surfactant concentration; (c) the position of the front xf and the rear xr of the liquid film; (d) maximal thickness and spreading radius of the liquid film.
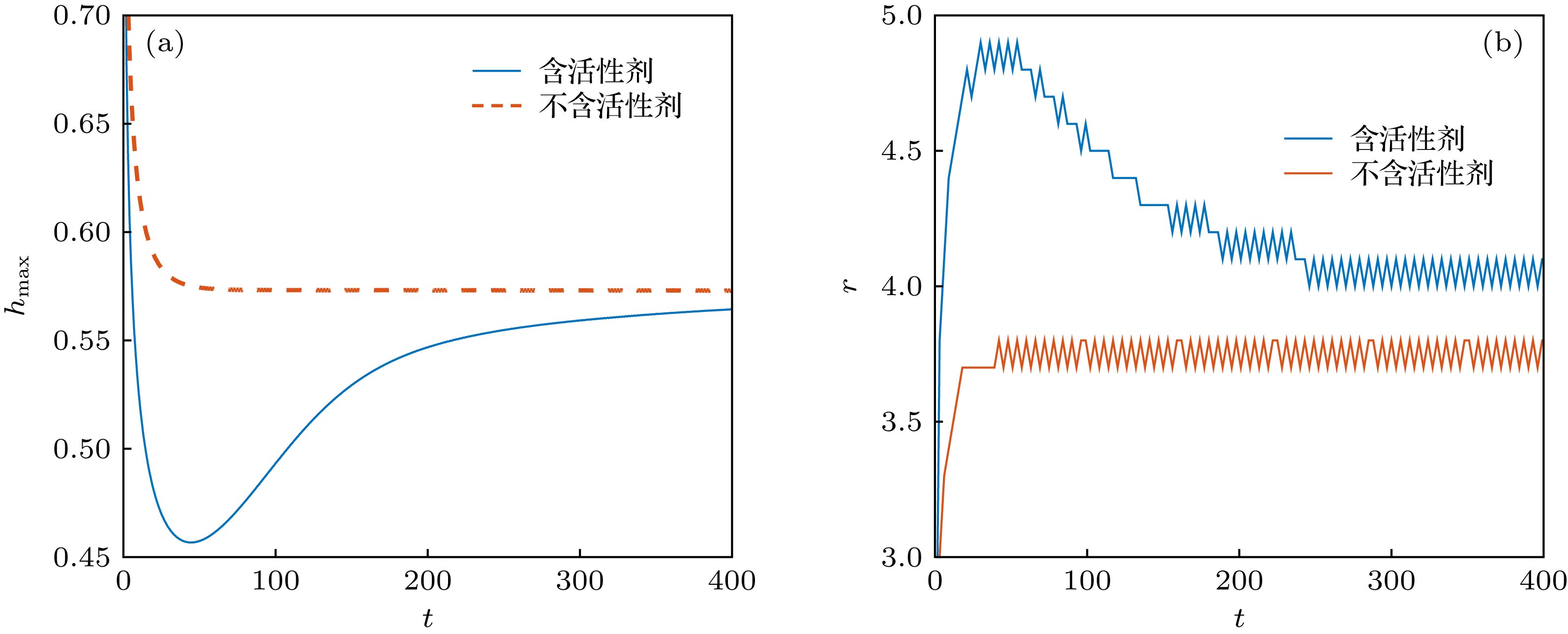
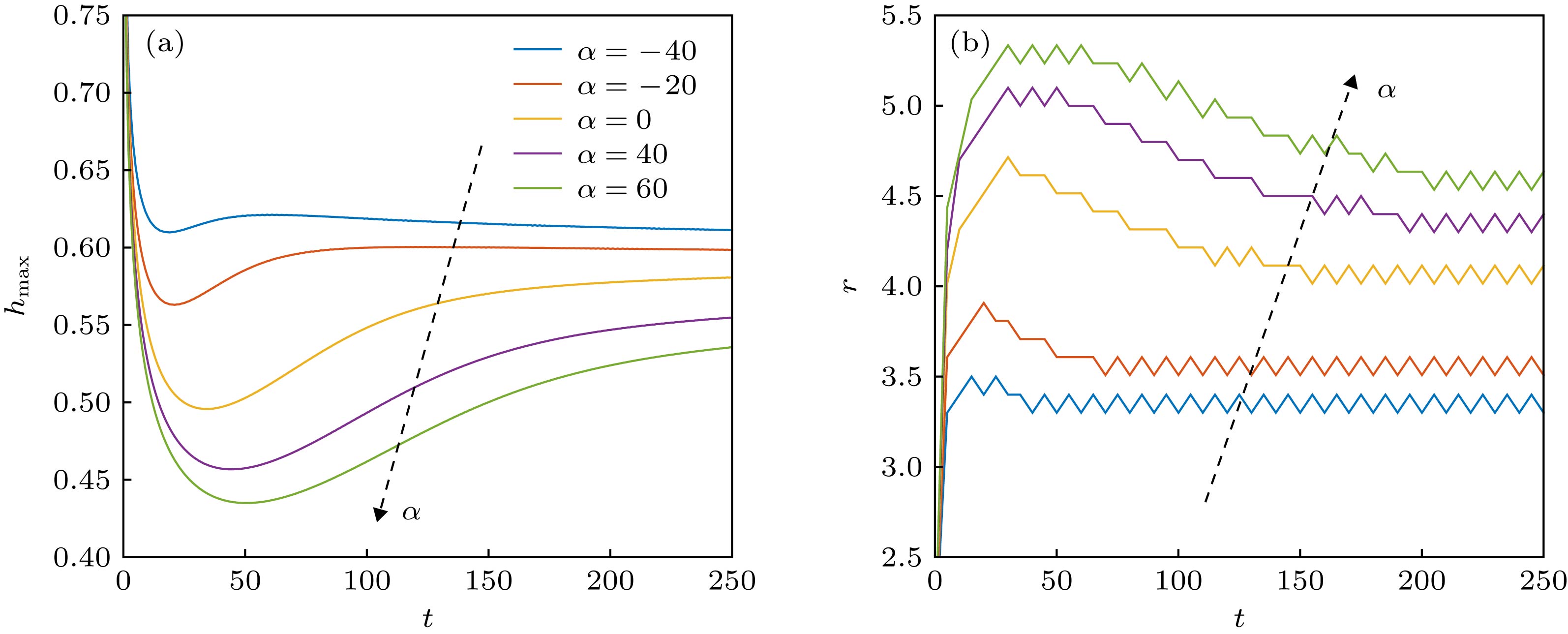
图 8 考虑活性剂影响和不考虑活性剂影响的液膜演化过程对比 (a)液膜最大厚度; (b)液膜铺展半径
Figure 8. Film spreading when both the capillary stress and the drift govern the dynamics of the film with (blue line) and without (orange line) considering the effect of surfactant: (a) Maximal thickness of the liquid film; (b) spreading radius of the liquid film.
图 10 不同α下部分润湿薄液膜的铺展过程对比 (a)最大厚度; (b)铺展半径
Figure 10. Evolution of partially wetting film with different values of α: (a) Maximal thickness of the liquid film; (b) spreading radius of the liquid film.
图 11 不同M下部分润湿薄液膜的铺展过程对比 (a)最大厚度; (b)铺展半径
Figure 11. Evolution of partially wetting film with different values of M: (a) Maximal thickness of the liquid film; (b) spreading radius of the liquid film.
表 1 有量纲参数取值范围
Table 1. Order of magnitude estimates for dimensional parameters.
有量纲参数 符号 单位 取值范围 表面张力系数 ${\varSigma ^ * }$ N·m2/mol 5 × 10–3 液膜无活性剂时表面张力 γ0* N/m 0.072 液体黏度 μ* Pa·s 0.001 液体密度 ρ* kg/m3 1000 SAW速度振幅 U * m/s 0.1—0.26 液膜最大厚度 H * m 10–7—9 × 10–6 液膜特征长度 L* m 10–5—9 × 10–4 临界胶束浓度 Gm* mol/L 0.0086 初始时刻最大活性剂浓度 G0* mol/L 0.002—0.0086 有量纲三相接触角 θ* (º) 3—28 表面扩散系数 Ds* m2/s 10–8—10–6 黏性渗透长度 ${\delta ^ * }$ m 10–7 
DownLoad: CSV
表 2 无量纲参数取值范围
Table 2. Order of magnitude estimates for nondimensional parameters.
无量纲参数 定义 取值范围 无量纲预置液膜厚度 hf 0.1 分离压稳定常数 C 0.5 初始活性剂浓度的
最大值G0 0.2—1 厚度小量 ε = (δ */H *)1/3 0.22—1 分离压与活性剂
浓度的相关系数α –100—100 无量纲三相接触角 θ = θ */120° 0.025—0.233 Marangoni数 $ M = \theta \varepsilon \varSigma ^ * G_m^ */{\rho ^ * }{\delta ^ * }{U^{ * 2} }$ 0.1—100 Weber数 We = ρ*U*2H*/γ0* 10–5—5 × 10-3 Reynolds数 Re = ρ*U*δ*/μ* 0.01—0.03 Peclet数 Pe = U*L*/Ds* 1—1000
DownLoad: CSV
-
[1] Bar-Cohen A, Arik M, Ohadi M 2006 Proc. IEEE 94 1549
Google Scholar
[2] Lee K S, Ivanova N, Starov V M, Hilal N, Dutschk V 2008 Adv. Colloid Interf. 144 54
Google Scholar
[3] Afsar-Siddiqui A B, Luckham P F, Matar O K 2003 Adv. Colloid Interf. 106 183
Google Scholar
[4] Brabcova Z, McHale G, Wells G G, Brown C V, Newton M I 2017 Appl. Phys. Lett. 110 121603
Google Scholar
[5] Wang Z, Varma V B, Wang Z P, Ramanujan R V 2015 J. Micromech. Microeng. 25 124001
Google Scholar
[6] Rezk A, Manor O, Yeo L Y, Friend J R 2014 Proc. R. Soc. A 470 20130765
Google Scholar
[7] Rezk A R, Manor O, Friend J R, Yeo L Y 2012 Nat. Commun. 3 1167
Google Scholar
[8] Altshuler G, Manor O 2015 Phys. Fluids 27 102103
Google Scholar
[9] Altshuler G, Manor O 2016 Phys. Fluids 28 72102
Google Scholar
[10] Manor O, Dentry M, Friend J R, Yeo L Y 2011 Soft Matter 7 7976
Google Scholar
[11] Manor O, Rezk A R, Friend J R, Yeo L Y 2015 Phys. Rev. E 91 53015
Google Scholar
[12] Collins D J, Manor O, Winkler A, Schmidt H, Friend J R, Yeo L Y 2012 Phys. Rev. E 86 56312
Google Scholar
[13] Qi A, Yeo L Y, Friend J R 2008 Phys. Fluids 20 74103
Google Scholar
[14] Warner M R E, Craster R V, Matar O K 2002 Phys. Fluids 14 1642
Google Scholar
[15] Schwartz L W, Roy R V 1999 J. Colloid Interface Sci. 218 309
Google Scholar
[16] Manev E D, Pugh R J 1991 Langmuir 7 2253
Google Scholar
[17] Bhakta A, Ruckenstein E 1997 Adv. Colloid Interf. 70 1
Google Scholar
[18] Incropera F P, Lavine A S, Bergman T L, DeWitt D P 2007 Fundamentals of Heat and Mass Transfer (6 ed.) (New York: John Wiley & Sons) p883
[19] Schwartz L W, Roy R V 2003 J. Colloid Interf. Sci. 264 237
Google Scholar
[20] Morozov M, Manor O 2017 J. Fluid Mech. 810 307
Google Scholar
[21] Riley N 1998 Theoret. Comput. Fluid Dyn. 10 349
Google Scholar
[22] Tiberg F, Cazabat A 1994 Langmuir 10 2301
Google Scholar
[23] Birch W R, Knewtson M A, Garoff S, Suter R M 1995 Langmuir 11 48
Google Scholar
[24] Dean D S, Sentenac D 1997 Europhys. Lett. 38 645
Google Scholar
[25] Hayduk W, Laudie H 1974 AIChE J. 20 611
Google Scholar
[26] Hu G, Xu A, Xu Z, Zhou Z 2008 Phys. Fluids 20 102101
Google Scholar
[27] 刘邱祖, 寇子明, 韩振南, 高贵军 2013 62 234701
Google Scholar
Liu Q Z, Kou Z M, Han Z N, Gao G J 2013 Acta Phys. Sin. 62 234701
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 7490
- PDF Downloads: 57
- Cited By: 0
