-
Nitrogen is the main reaction and detonation product of energetic materials. Therefore, studying the equation of state and phase transition of nitrogen at high temperature and high pressure is very important in evaluating the energy characteristics of energetic materials, especially in designing a new-generation nitrogen-rich energetic materials. Using density functional molecular dynamics simulation method, we calculate the pressure, internal energy and chemical components of fluid nitrogen in a temperature range of 900–25000 K and a pressure range of 2–300 GPa. The negative changes of pressure with temperature on isochores are observed under the temperature and pressure conditions of 3000–10000 K and 20–80 GPa. As the temperature increases, the pressure drop is caused by the collapse of nitrogen molecules. This phenomenon is related to the phase transition from molecular fluid nitrogen to polymerized fluid nitrogen. The triple bond in the molecule breaks and a polymer forms, which is connected by single and double bonds with neighboring atom. We also study the equation of state along Hugoniot curve under impact loading. The obtained Hugoniot curve is in good agreement with the experimental results. It is found that the softening of the experimental curve in a range of 30–60 GPa is related to the decomposition of nitrogen molecules and the formation of polymeric nitrogen.
-
Keywords:
- fluid nitrogen /
- density functional molecular dynamics simulation /
- equation of state /
- phase transition /
- high temperature and high pressure
[1] Ree R H 1984 J. Chem. Phys. 81 1251
Google Scholar
[2] Samartzis P C, Wodtke A M 2006 Int. Rev. Phys. Chem. 25 527
Google Scholar
[3] Christian R H, Duff R E, Yarger F L 1955 J. Chem. Phys. 23 2045
Google Scholar
[4] Mulder A, Michels J P J, Schouten J A 1996 J. Chem. Phys. 105 3235
Google Scholar
[5] Mailhiot C, Yang L H, McMahan A K 1992 Phys. Rev. B 46 14419
Google Scholar
[6] Zahariev F, Hooper J, Alavi S, Zhang F, Woo T K 2007 Phys. Rev. B 75 140101
Google Scholar
[7] Pickard C J, Needs R J 2009 Phys. Rev. Lett. 102 125702
Google Scholar
[8] Ma Y M, Oganov A R, Li Z W, Xie Y, Kotakoski J 2009 Phys. Rev. Lett. 102 065501
Google Scholar
[9] Wang X L, Wang Y C, Miao M S, Zhong X, Lv J, Cui T, Li J F, Chen L 2012 Phys. Rev. Lett. 109 175502
Google Scholar
[10] Hirshberg B, Gerber R B, Krylovc A I 2014 Nat. Chem. 6 52
Google Scholar
[11] Li Y W, Feng X L, Liu H Y, Hao J 2018 Nat. Commun. 9 72
Google Scholar
[12] Eremets M I, Gavriliuk A G, Trojan I A, Dzivenko D A, Boehler R 2004 Nat. Mater. 3 558
Google Scholar
[13] Tomasino D, Kim M, Smith J, Yoo C 2014 Phys. Rev. Lett. 113 205502
Google Scholar
[14] Ji C, Adeleke A A, Yang L, Wan B, Gou H Y, Yao Y S, Li B, Meng Y, Smith J S, Prakapenka V B, Liu W J, Shen G Y, Mao W L, Mao H K 2020 Sci. Adv. 6 eaba9206
Google Scholar
[15] Laniel D, Winkler B, Fedotenko T, Pakhomova A, Chariton S, Milman V, Prakapenka V, Dubrovinsky L, Dubrovinskaia N 2020 Phys. Rev. Lett. 124 216001
Google Scholar
[16] Liu Y, Su H P, Niu C P, Wang X L, Zhang J R, Ge Z X, Li Y C 2020 Chin. Phys. B 29 106201
Google Scholar
[17] 梁冬梅, 刘海燕, 甘云丹, 匡安龙, 田春玲 2021 科学通报 66 2908
Google Scholar
Liang D M, Liu H Y, Gan Y D, Kuang A L, Tian C L 2021 Chin. Sci. Bull. 66 2908
Google Scholar
[18] Liu S J, Zhao L, Yao M G, Miao MS, Liu B B 2020 Adv. Sci. 7 1902320
Google Scholar
[19] Dick R D 1970 J. Chem. Phys. 52 6021
Google Scholar
[20] Nellis W J, Holmes N C, Mitchell A C, Thiel M V 1980 J. Chem. Phys. 73 15
Google Scholar
[21] Nellis W J, Radousky H B, Hamilton D C, Mitchell A C, Holmes N C, Christianson K B, Thiel M V 1991 J. Chem. Phys. 94 2244
Google Scholar
[22] Akram M S, Fan Z N, Zhang M J, Liu Q J, Liu F S 2020 J. Appl. Phys. 128 225901
Google Scholar
[23] Ross M 1987 J. Chem. Phys. 86 7110
Google Scholar
[24] Nellis W J, Holmes N C, Mitchell A C, Thiel M 1984 Phys. Rev. Lett. 53 1661
Google Scholar
[25] Militzer B, Ceperley D M, Kress J D, Johnson J D, Collins L A, Mazevet S 2001 Phys. Rev. Lett. 87 275502
Google Scholar
[26] 马桂存, 张其黎, 宋红州, 李琼, 朱希睿, 孟续军 2017 66 036401
Google Scholar
Ma G C, Zhang Q L, Song H Z, Li Q, Zhu X R, Meng X J 2017 Acta Phys. Sin. 66 036401
Google Scholar
[27] Driver K P, Militzer B 2016 Phys. Rev. B 93 064101
Google Scholar
[28] Zhao G, Wang H, Ding M C, Zhao X G, Wang H Y, Yan J L 2018 Phys. Rev. B 98 184205
Google Scholar
[29] Kress J, Mazevet S, Collins L A, Wood W 2000 Phys. Rev. B 63 024203
Google Scholar
[30] Boates B, Bonev S A 2009 Phys. Rev. Lett. 102 015701
Google Scholar
[31] Boates B, Bonev S A 2011 Phys. Rev. B 83 174114
Google Scholar
[32] Geng H Y, Wu Q, Marqués M, Ackland G J 2019 Phys. Rev. B 100 134109
Google Scholar
[33] Kresse G, Furthmuller J 1996 Phys. Rev. B 54 11169
Google Scholar
[34] Perdew J P, Burke K, Ernzerhof M 1996 Phys. Rev. Lett. 77 3865
Google Scholar
[35] Blöchl P E 1994 Phys. Rev. B 50 17953
Google Scholar
[36] Nose S C 1984 J. Chem. Phys. 81 511
Google Scholar
[37] Shan H, Yang Y, James A J, Sharp P R 1997 Science 275 1460
Google Scholar
[38] Steele B A, Oleynik I I 2016 Chem. Phys. Lett. 643 21
Google Scholar
-
图 1 1.75 g/cm3时流体氮的等容线 (a)压强-温度关系; (b) 内能-温度关系; (c)原子平均配位数随温度的变化; (d) 化学组分占比(Rn)与离解度(β)随温度的变化; (e) 径向分布函数图像; (f)—(h)不同温度下的原子分布抽样, 绿色原子代表氮分子组分, 玫色表示聚合物组分, 蓝色小球表示氮原子组分, 红色三角形代表液氮的Hugoniot状态点
Figure 1. Fluid nitrogen at 1.75 g/cm3: (a) Temperature-dependence for pressure ; (b) temperature-dependence for internal energy; (c) temperature-dependence for coordination number of atoms; (d) temperature-dependence of chemical component ratio (Rn) and molecular dissociation degree (β) ; (e) pair correlation functions at temperatures of 7000, 10000 and 20000 K; (f)–(h) snapshots from MD simulations. Green atoms represent molecules, the red spheres show polymers and the blue indicate isolated atoms. The red triangle represent the Hugoniot point.
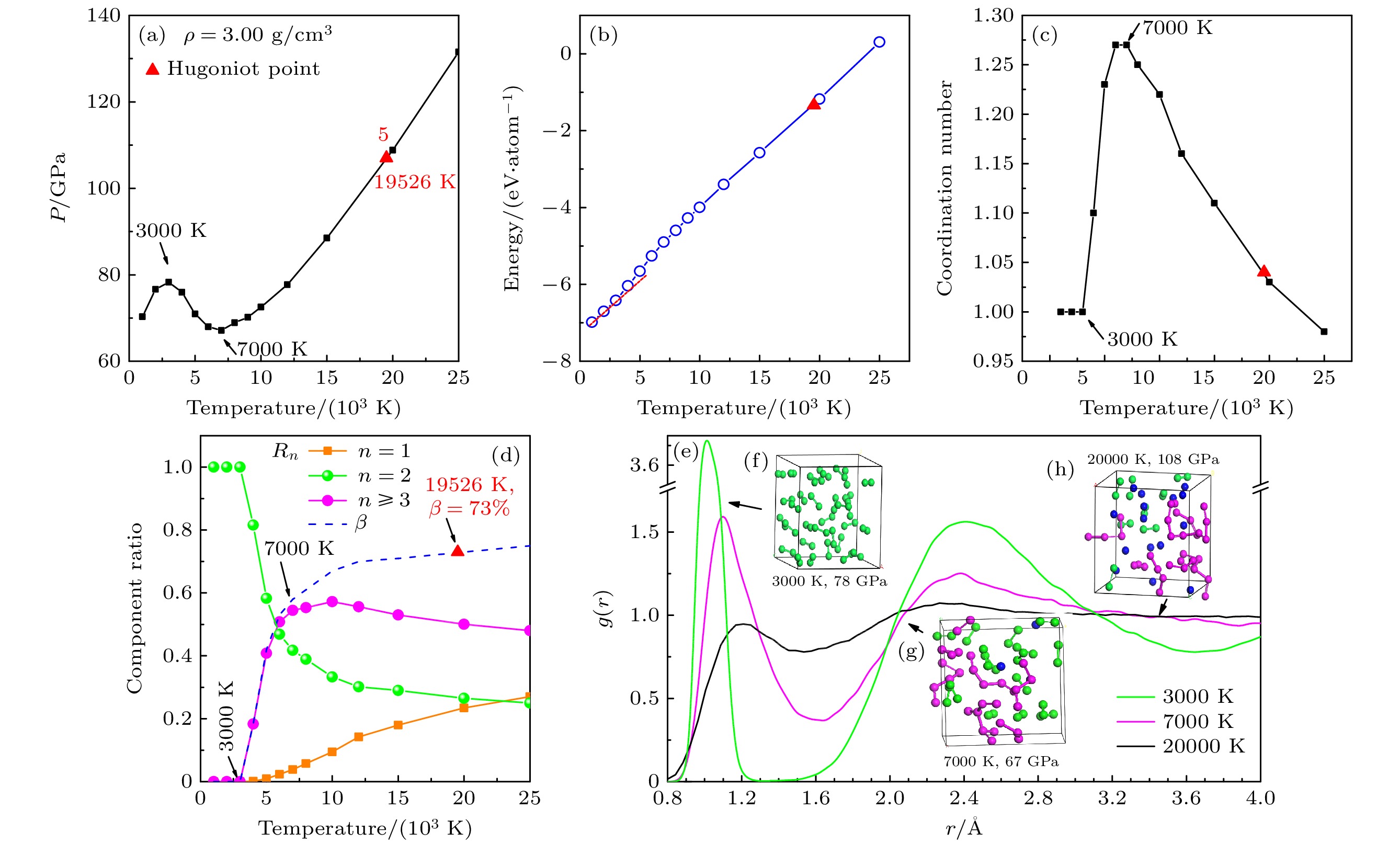
图 2 3.00 g/cm3时流体氮的等容线 (a)压强-温度关系; (b) 内能-温度关系; (c)原子平均配位数随温度的变化; (d) 化学组分占比Rn 与离解度β随温度的变化; (e) 径向分布函数; (f)—(h) 不同温度下的模拟原胞原子的瞬态抽样
Figure 2. Nitrogen isochore at 3.00 g/cm3: (a) Temperature-dependence for pressure ; (b) temperature-dependence for internal energy; (c) temperature-dependence for coordination number of atoms; (d) temperature-dependence of chemical component ratio (Rn) and molecular dissociation degree (β) ; (e) pair correlation functions at temperatures of 3000, 70000 and 20000 K; (f)–(h) snapshots from MD simulations at different temperatures.
图 3 在不同的温度和密度下流体氮结构的价电荷密度 (a) 1.75 g/cm3, 2000 K; (b) 1.75 g/cm3, 20000 K; (c) 3.00 g/cm3, 7000 K; (d) 3.00 g/cm3, 20000 K
Figure 3. Valance charge densities of fluid nitrogen at different temperatures and densities: (a) 1.75 g/cm3, 2000 K; (b) 1.75 g/cm3, 20000 K; (c) 3.00 g/cm3, 7000 K; (d) 3.00 g/cm3, 20000 K.
图 4 液氮的Hugoniot物态方程的实验和理论结果比较 (a)压强-密度关系; (b)温度-压强关系
Figure 4. Comparison between the experiments and calculations of Hugoniot equation of state for liquid nitrogen: (a) Pressure as a function of the final shock density; (b) shock temperature as a function of the pressure.
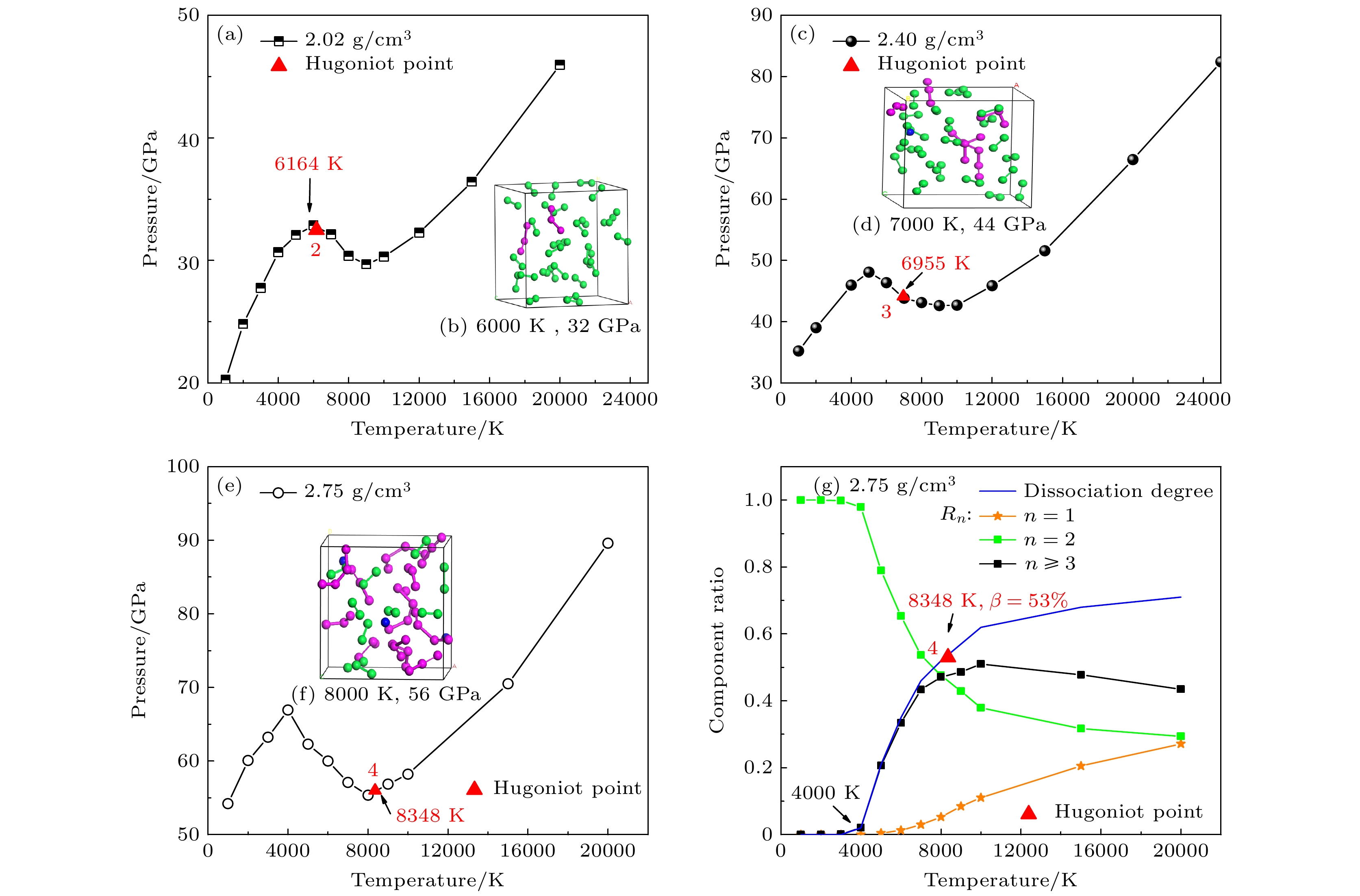
图 5 液氮的Hugoniot冲击压缩点在不同等容线上的压强-温度相空间分布 (a) 2.02 g/cm3; (c) 2.40 g/cm3; (e) 2.75 g/cm3; 图(b), (d), (f)是与图(a), (c), (e)相对应的分子动力学模拟中原胞原子位置分布的的瞬态抽样. (g) 2.75 g/cm3下流体氮的组分
Figure 5. Hugoniot points in P/T space at constant densities: (a) 2.02 g/cm3; (c) 2.40 g/cm3; (e) 2.75 g/cm3; (b), (d), (f) corresponding snapshots from MD simulations of panels (a), (c), (e). (g) Chemical components at 2.75 g/cm3.
表 1 DFT-MD模拟得到的液氮冲击状态数据以及流体组分(初态ρ0 = 0.808 g/cm3, T0 = 77.6 K, E0 = –8.319 eV/atom)
Table 1. Calculated results for pressure and temperature and the chemical components along the Hugoniot curve from our DFT-MD simulations. The initial conditions are ρ0 = 0.808 g/cm3, T0 = 77.6 K, E0 = –8.319 eV/atom.
ρ/
(g·cm–3)P/GPa T/K Dissociation degree
($ \beta $)Polymeric ratio
($ {R_{n \geqslant {\text{3}}}} $)Label number 1.5 7.2 900 0 0 1.75 16.3 2295 0 0 1 1.92 24.1 4109 0 0 2.02 32.5 6164 0.03 0.03 2 2.20 38.3 6582 0.14 0.12 2.40 44.1 6955 0.27 0.25 3 2.53 47.9 7246 0.37 0.35 2.75 56.5 8348 0.53 0.47 4 2.90 67.2 10397 0.65 0.55 3.00 106.8 19526 0.73 0.51 5 
DownLoad: CSV
-
[1] Ree R H 1984 J. Chem. Phys. 81 1251
Google Scholar
[2] Samartzis P C, Wodtke A M 2006 Int. Rev. Phys. Chem. 25 527
Google Scholar
[3] Christian R H, Duff R E, Yarger F L 1955 J. Chem. Phys. 23 2045
Google Scholar
[4] Mulder A, Michels J P J, Schouten J A 1996 J. Chem. Phys. 105 3235
Google Scholar
[5] Mailhiot C, Yang L H, McMahan A K 1992 Phys. Rev. B 46 14419
Google Scholar
[6] Zahariev F, Hooper J, Alavi S, Zhang F, Woo T K 2007 Phys. Rev. B 75 140101
Google Scholar
[7] Pickard C J, Needs R J 2009 Phys. Rev. Lett. 102 125702
Google Scholar
[8] Ma Y M, Oganov A R, Li Z W, Xie Y, Kotakoski J 2009 Phys. Rev. Lett. 102 065501
Google Scholar
[9] Wang X L, Wang Y C, Miao M S, Zhong X, Lv J, Cui T, Li J F, Chen L 2012 Phys. Rev. Lett. 109 175502
Google Scholar
[10] Hirshberg B, Gerber R B, Krylovc A I 2014 Nat. Chem. 6 52
Google Scholar
[11] Li Y W, Feng X L, Liu H Y, Hao J 2018 Nat. Commun. 9 72
Google Scholar
[12] Eremets M I, Gavriliuk A G, Trojan I A, Dzivenko D A, Boehler R 2004 Nat. Mater. 3 558
Google Scholar
[13] Tomasino D, Kim M, Smith J, Yoo C 2014 Phys. Rev. Lett. 113 205502
Google Scholar
[14] Ji C, Adeleke A A, Yang L, Wan B, Gou H Y, Yao Y S, Li B, Meng Y, Smith J S, Prakapenka V B, Liu W J, Shen G Y, Mao W L, Mao H K 2020 Sci. Adv. 6 eaba9206
Google Scholar
[15] Laniel D, Winkler B, Fedotenko T, Pakhomova A, Chariton S, Milman V, Prakapenka V, Dubrovinsky L, Dubrovinskaia N 2020 Phys. Rev. Lett. 124 216001
Google Scholar
[16] Liu Y, Su H P, Niu C P, Wang X L, Zhang J R, Ge Z X, Li Y C 2020 Chin. Phys. B 29 106201
Google Scholar
[17] 梁冬梅, 刘海燕, 甘云丹, 匡安龙, 田春玲 2021 科学通报 66 2908
Google Scholar
Liang D M, Liu H Y, Gan Y D, Kuang A L, Tian C L 2021 Chin. Sci. Bull. 66 2908
Google Scholar
[18] Liu S J, Zhao L, Yao M G, Miao MS, Liu B B 2020 Adv. Sci. 7 1902320
Google Scholar
[19] Dick R D 1970 J. Chem. Phys. 52 6021
Google Scholar
[20] Nellis W J, Holmes N C, Mitchell A C, Thiel M V 1980 J. Chem. Phys. 73 15
Google Scholar
[21] Nellis W J, Radousky H B, Hamilton D C, Mitchell A C, Holmes N C, Christianson K B, Thiel M V 1991 J. Chem. Phys. 94 2244
Google Scholar
[22] Akram M S, Fan Z N, Zhang M J, Liu Q J, Liu F S 2020 J. Appl. Phys. 128 225901
Google Scholar
[23] Ross M 1987 J. Chem. Phys. 86 7110
Google Scholar
[24] Nellis W J, Holmes N C, Mitchell A C, Thiel M 1984 Phys. Rev. Lett. 53 1661
Google Scholar
[25] Militzer B, Ceperley D M, Kress J D, Johnson J D, Collins L A, Mazevet S 2001 Phys. Rev. Lett. 87 275502
Google Scholar
[26] 马桂存, 张其黎, 宋红州, 李琼, 朱希睿, 孟续军 2017 66 036401
Google Scholar
Ma G C, Zhang Q L, Song H Z, Li Q, Zhu X R, Meng X J 2017 Acta Phys. Sin. 66 036401
Google Scholar
[27] Driver K P, Militzer B 2016 Phys. Rev. B 93 064101
Google Scholar
[28] Zhao G, Wang H, Ding M C, Zhao X G, Wang H Y, Yan J L 2018 Phys. Rev. B 98 184205
Google Scholar
[29] Kress J, Mazevet S, Collins L A, Wood W 2000 Phys. Rev. B 63 024203
Google Scholar
[30] Boates B, Bonev S A 2009 Phys. Rev. Lett. 102 015701
Google Scholar
[31] Boates B, Bonev S A 2011 Phys. Rev. B 83 174114
Google Scholar
[32] Geng H Y, Wu Q, Marqués M, Ackland G J 2019 Phys. Rev. B 100 134109
Google Scholar
[33] Kresse G, Furthmuller J 1996 Phys. Rev. B 54 11169
Google Scholar
[34] Perdew J P, Burke K, Ernzerhof M 1996 Phys. Rev. Lett. 77 3865
Google Scholar
[35] Blöchl P E 1994 Phys. Rev. B 50 17953
Google Scholar
[36] Nose S C 1984 J. Chem. Phys. 81 511
Google Scholar
[37] Shan H, Yang Y, James A J, Sharp P R 1997 Science 275 1460
Google Scholar
[38] Steele B A, Oleynik I I 2016 Chem. Phys. Lett. 643 21
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 4893
- PDF Downloads: 87
- Cited By: 0
