-
Based on the electromagnetic properties of all-dielectric optical metamaterial, an all-dielectric metasurface of lattice-perturbed nanohole array is proposed to excite a multiple Fano resonance in the near-infrared region. Combined with the group theory, the formation mechanism and evolution law of multiple Fano resonances in this structure when its unit cell is a square lattice configuration and the square lattice symmetry is broken are explored in depth. The results show that double degenerate mode directly excited by the normal incident plane wave is coupled to vertical free-space radiation continuum to form double Fano resonance when unit cell is symmetrical, while the uncoupled non-degenerate modes excited by the normal incident plane wave is coupled to vertical free-space radiation continuum to form triple Fano resonance with higher Q factor when the symmetry is broken. Numerical simulation is used to explore the influences of x-polarized and y-polarized plane wave on the above Fano resonances, and the results show that the Fano resonance of double degenerate resonance is polarization independent, while the non-degenerate resonance is polarization dependent. The findings in this work can provide an effective theoretical reference for designing other square lattice metasurface to realize the excitation and evolution of multiple Fano resonances.
-
Keywords:
- all-dielectric metamaterial /
- group theory /
- multiple Fano resonance /
- lattice perturbation
[1] 鹿利单, 祝连庆, 曾周末, 崔一平, 张东亮, 袁配 2021 70 034204
Google Scholar
Lu L D, Zhu L Q, Zeng Z M, Cui Y P, Zhang D L, Yuan P 2021 Acta Phys. Sin. 70 034204
Google Scholar
[2] Tribelsky M I, Miroshnichenko A E 2016 Phys. Rev. A 93 053837
Google Scholar
[3] Kong X H, Xiao G B 2016 J. Opt. Soc. Am. A 33 707
Google Scholar
[4] Poddubny A N, Rybin M V, Limonov M F, Kivshar Y S 2012 Nat. Commun. 3 914
Google Scholar
[5] Rybin M V, Mingaleev S F, Limonov M F, Kivshar Y S 2016 Sci. Rep. 6 20599
Google Scholar
[6] Rybin M V, Khanikaev A B, Inoue M, Samusev K B, Steel M J, Yushin G, Limonov M F 2009 Phys. Rev. Lett. 103 023901
Google Scholar
[7] Sharac, N, Sharma H, Veysi M, Sanderson R N, Khine M, Capolino F, Ragan R 2016 Nanotechnology 27 105302
Google Scholar
[8] Guo M, Huang L R, Liu W B, Ding J F 2021 Opt. Mater. 112 110802
Google Scholar
[9] Wang W D, Zheng L, Wang Y L 2020 Opt. Commun. 454 124516
Google Scholar
[10] Kong Y, Cao J J, Qian W C, Liu C, Wang S Y 2018 IEEE Photon. J. 10 1943
Google Scholar
[11] Zhang Y H, Liang Z Z, Meng D J, Qin Z, Fan Y D, Shi X Y, Smith D R, Hou E Z 2021 Results Phys. 24 104129
Google Scholar
[12] Brandl D W, Mirin N A, Nordlander P 2006 J. Phys. Chem. B 110 12302
Google Scholar
[13] Hopkins B, Poddubny A N, Miroshnichenko A E, Kivshar Y S 2013 Phys. Rev. A (Coll Park) 88 053819
Google Scholar
[14] Forestiere C, Negro L D, Miano G 2013 Phys. Rev. B 88 155411
Google Scholar
[15] Gomez D E, Vernon K C, Davis T J 2010 Phys. Rev. B 81 075414
Google Scholar
[16] Johnson P B, Christy R W 1972 Phys. Rev. B 6 4370
Google Scholar
[17] Chen Q, Wang D, Gao F 2021 Opt. Lett. 46 1209
Google Scholar
[18] Ito T, Sakoda K 2001 Phys. Rev. B 64 045117
Google Scholar
[19] Crozier K B, Lousse V, Kilic O, Kim S, Fan S, Solgaard O 2006 Phys. Rev. B 73 115126
Google Scholar
[20] 崔成聪 2020 博士学位论文 (武汉: 华中科技大学)
Cui C C 2020 Ph. D. Dissertation (Wuhang: Huazhong University of Science and Technology) (in Chinese)
[21] Kilic O, Digonnet M, Kino G, Solgaard O 2008 Opt. Express 16 13090
Google Scholar
[22] Nicolaou C, Lau W T, Gad R, Akhavan H, Schilling R, Levi O 2013 Opt. Express 21 31698
Google Scholar
[23] Fan S H 2002 Phys. Rev. B 65 235112
Google Scholar
[24] Liu S D, Yang Z, Liu R P, Li X Y 2012 ACS Nano 6 6260
Google Scholar
[25] Rajratan B, Atwood L J 2019 Opt. Express 27 282
Google Scholar
[26] Lee J, Zhen B, Chua S L, Qiu W J, Joannopoulos J D, Soljacic M, Shapira O 2012 Phys. Rev. Lett. 109 067401
Google Scholar
[27] Staude I, Schilling J 2017 Nat. Photonics 11 274
Google Scholar
-
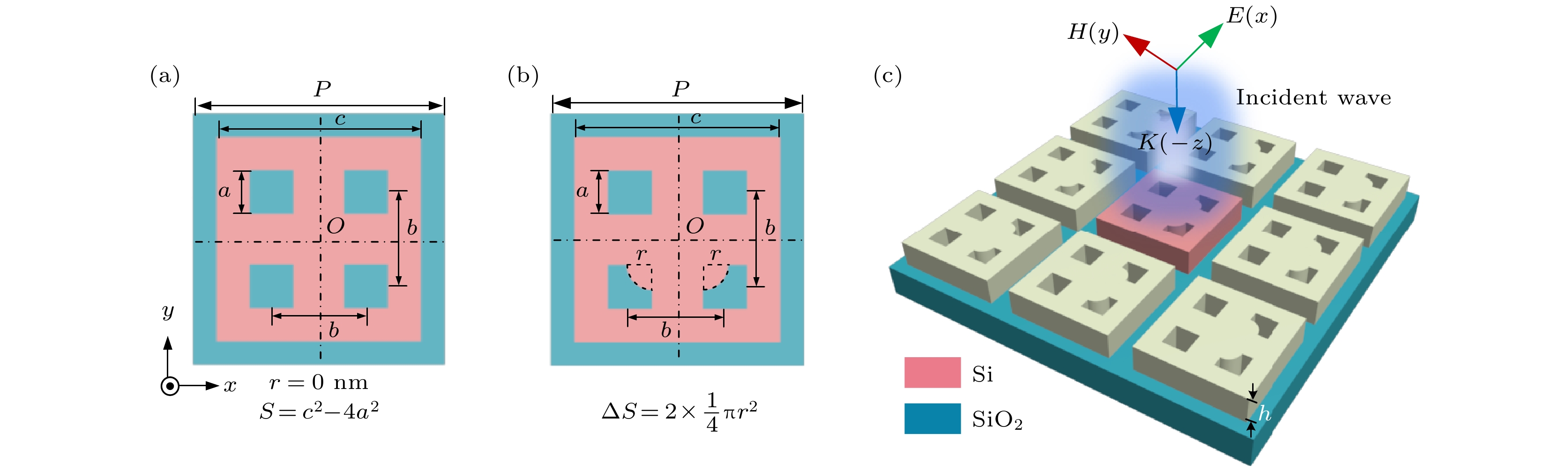
图 1 晶格扰动介质纳米孔阵列超构表面模型表征 (a) 方形晶格原胞俯视图; (b) 晶格扰动原胞俯视图; (c)
$ r = 80\;{\text{nm}} $ 时晶格扰动超构表面示意图Figure 1. Schematic diagram of dielectric nanohole arrays metasurface with lattice-perturbed: (a) Top view of unit cell with square lattice; (b) top view of unit cell with lattice-perturbed; (c) schematic diagram of metasurface with lattice-perturbed of
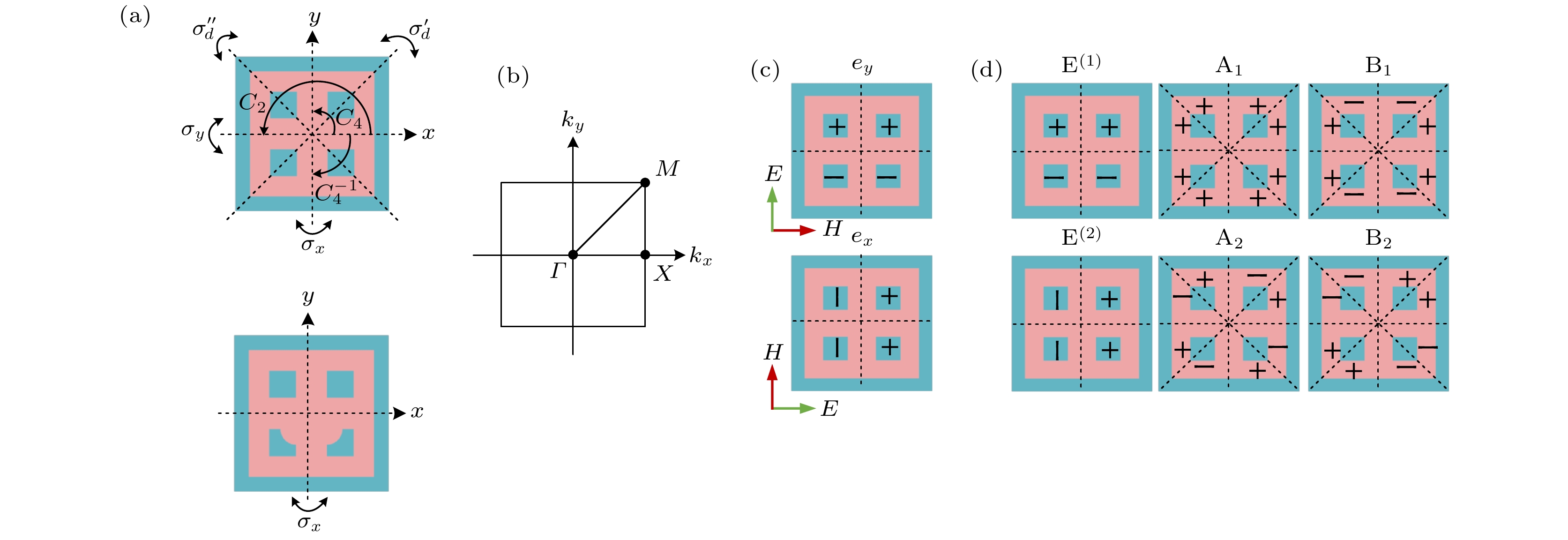
$ r = 80\;{\text{nm}} $ .
图 2 原胞与模场对称性 (a) 方形晶格(上)与晶格扰动(下)原胞的二维对称示意图; (b) 方形晶格超构表面的第一布里渊区; (c) y极化平面波(
$ {e_y} $ )与x极化平面波($ {e_x} $ )的模场对称性; (d) 方形晶格超构表面中6种本征模的对称性(同号区域对称, 异号区域反对称)Figure 2. Symmetry of unit cell and mode field: (a) Two-dimensional symmetry operation for unit cell with square lattice(above) and lattice-perturbed (below); (b) the first Brillouin zone of square lattice metasurface; (c) symmetry of resonant mode field of
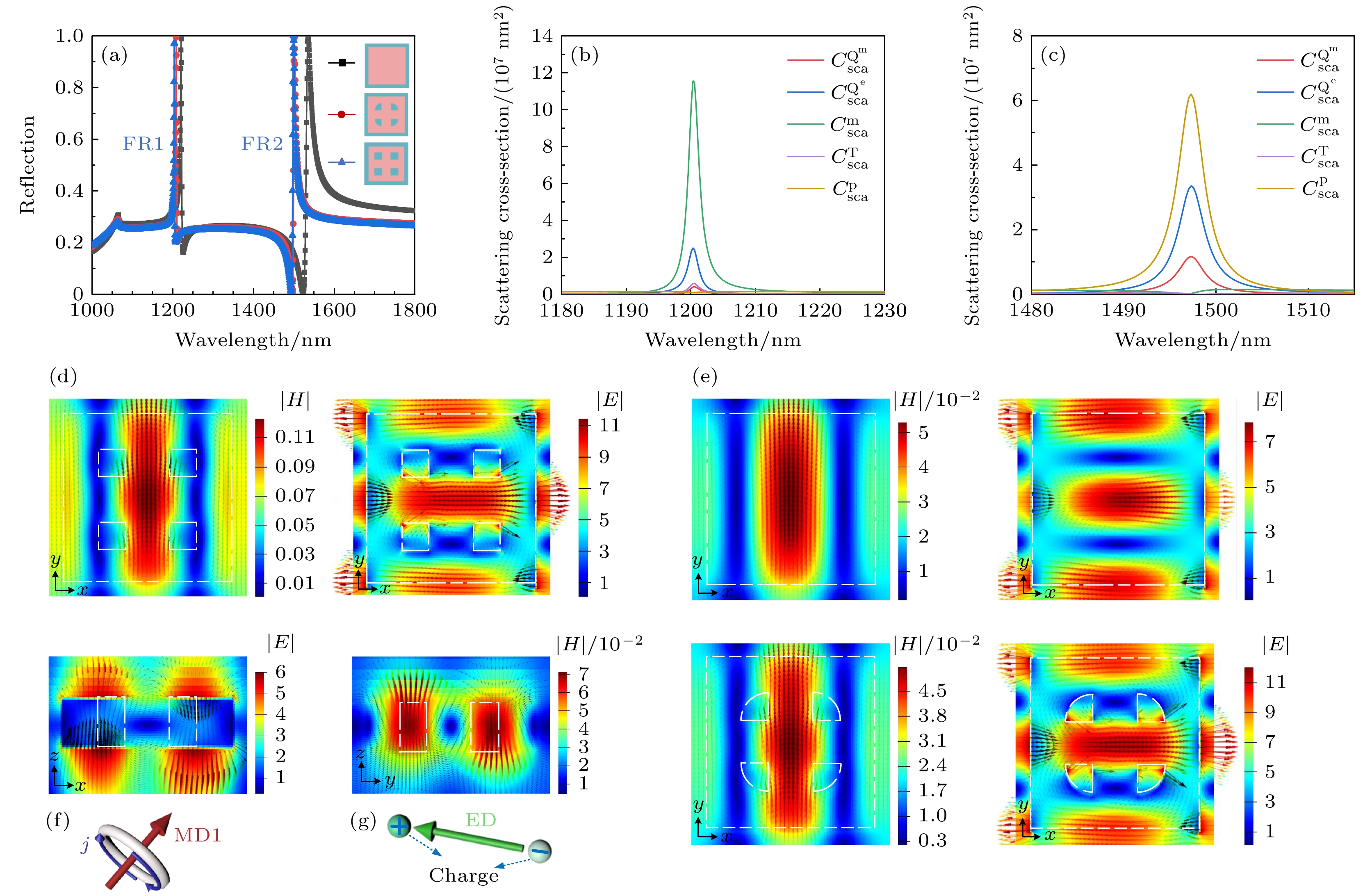
$ {e_y} $ and$ {e_x} $ ; (d) symmetry of six eigenmodes in lattice metasurface (areas with the same sign are symmetrical and areas with different signs are antisymmetric).
图 3 方形晶格超构表面在
$ {e_x} $ 正入射条件下的数值模拟结果 (a) 完整硅板、扇形孔与方孔超构表面的反射光谱对比图; (b), (c) FR1与FR2处的笛卡尔多极分解; (d) FR1(FR2)在xoy截面的归一化磁场(电场)分布$ \left| H \right| $ ($ \left| E \right| $ )及xoz(yoz)截面的归一化电场(磁场)分布$ \left| E \right| $ ($ \left| H \right| $ ); (e) 完整硅板与扇形孔超构表面在xoy截面的归一化电磁场分布(以下场图中的白线框均表征结构轮廓); (f), (g) MD1与ED的概念描述图Figure 3. Numerical simulation of square lattice metasurface under
$ {e_x} $ : (a) Reflectance spectrum comparison of metasurfaces with complete silicon block, scalloped holes and square holes; (b), (c) cartesian multipole decomposition of FR3, FR4 and FR5; (d) normalized magnetic(electric) field distributionin$ \left| H \right| $ ($ \left| E \right| $ ) in xoy section and normalized electric(magnetic) field distribution$ \left| E \right| $ ($ \left| H \right| $ )in xoz (yoz) sectionof FR1(FR2); (e) normalized electromagnetic field distribution in xoy section of metasurface with complete silicon block, scalloped holes(white boxes in the following field diagrams is structural outline drawing); (f), (g) conceptual description of MD1 and ED.
图 4 晶格扰动超构表面的反射光谱图与拟合曲线模型 (a)
$ {e_x} $ 与$ {e_y} $ 正入射条件下的反射光谱对比图; (b)$ {e_x} $ 正入射条件下FR1-FR5的拟合曲线Figure 4. Reflection spectra and fitting curve model of lattice perturbed metasurface: (a) Comparison of reflectance spectrum under
$ {e_x} $ and$ {e_y} $ ; (b) fitting curve of FR1-FR5 under$ {e_x} $ .
图 5 晶格扰动超构表面在
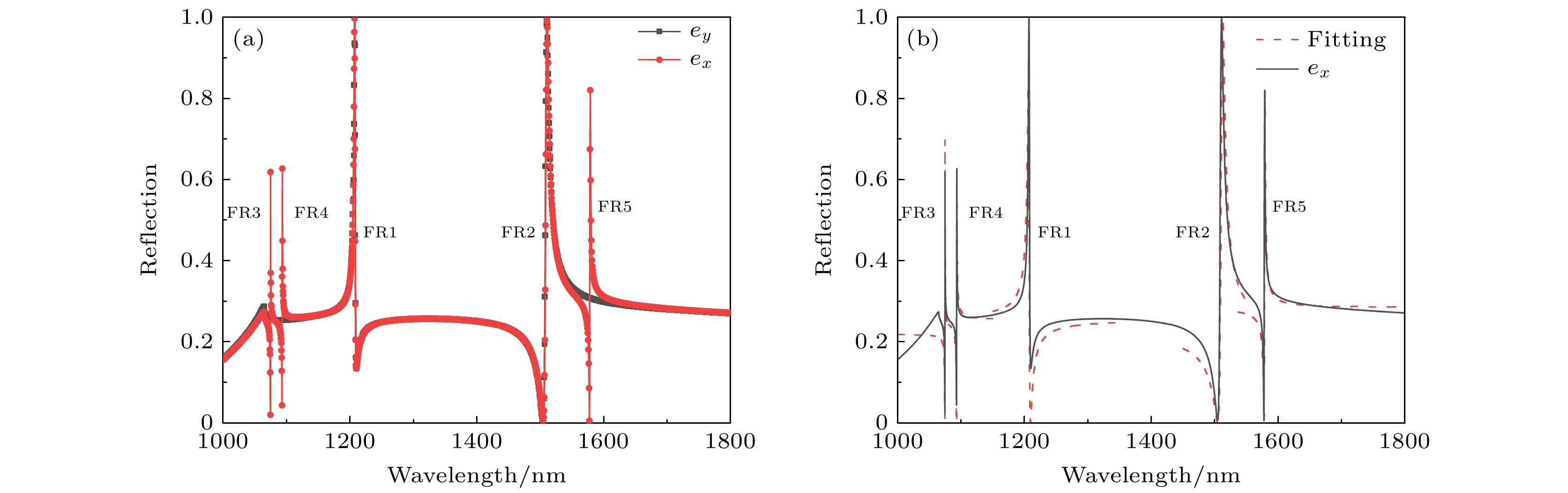
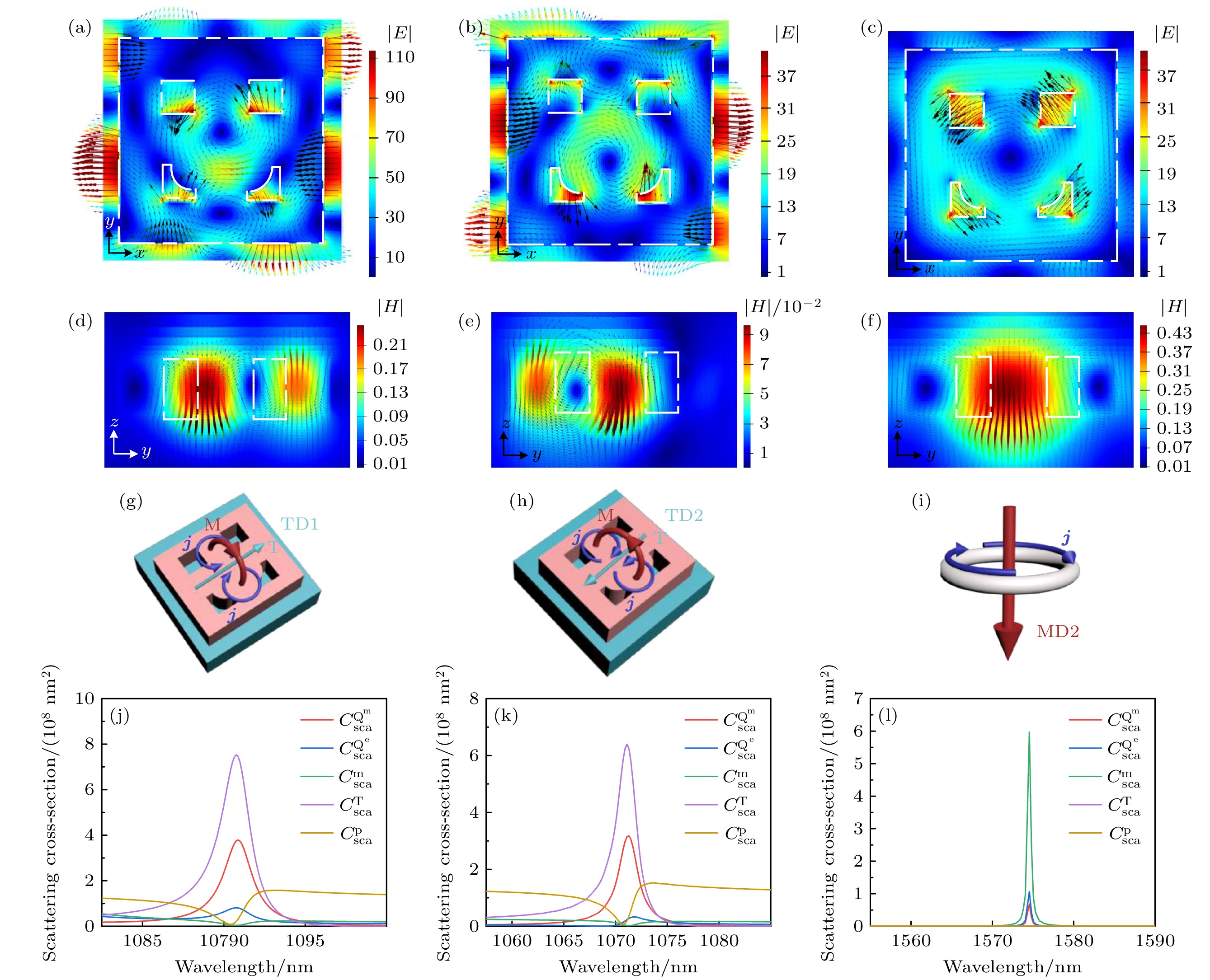
$ {e_x} $ 正入射条件下的近场分析与笛卡尔多极分解 (a)—(i) FR3, FR4与FR5在xoy截面的归一化电场分布$ \left| E \right| $ 、yoz截面的归一化磁场分布$ \left| H \right| $ 及TD1, TD2与MD2的概念描述图; (j)—(l) FR3, FR4与FR5处的笛卡尔多极分解Figure 5. Near-field analysis of lattice-perturbed metasurface under
$ {e_x} $ and cartesian multipole decomposition: (a)–(i) Normalized electric field distribution$ \left| E \right| $ in xoy section and normalized magnetic field distribution$ \left| H \right| $ in yoz sectionof FR3, FR4 and FR5, and conceptual description of TD1, TD2 and MD2; (j)–(l) cartesian multipole decomposition of FR3, FR4 and FR5.
图 6 晶格扰动超构表面在
$ {e_y} $ 正入射条件下的近场分布 (a) 共振1(共振2)在xoy截面的归一化磁场(电场)分布$ \left| H \right| $ ($ \left| E \right| $ )及yoz(xoz)截面的归一化电场(磁场)分布$ \left| E \right| $ ($ \left| H \right| $ ); (b) 共振1与共振2处的笛卡尔多极分解Figure 6. Near-field distribution of lattice-perturbed metasurface under
$ {e_y} $ : (a) Normalized magnetic(electric) field distributionin$ \left| H \right| $ ($ \left| E \right| $ ) in xoy section and normalized electric(magnetic) field distribution$ \left| E \right| $ ($ \left| H \right| $ ) in yoz(xoz) sectionof resonance 1(resonance 2); (b) cartesian multipole decomposition of resonance 1 and resonance 2.表 1
${C_{{\text{4v}}}}$ 点群的不可约表示的特征标表Table 1. Character table of irreducible representations of
${C_{{\text{4v}}}}$ point group.$ {C_{{\text{4 v}}}} $ E $ 2{C_4} $ $ {C_2} $ $ 2{\sigma _{\text{v}}} $ $ {\text{2}}{\sigma _{\text{d}}} $ $ {A_1} $ 1 1 1 1 1 $ {A_2} $ 1 1 1 –1 –1 $ {B_1} $ 1 –1 1 1 –1 $ {B_2} $ 1 –1 1 –1 1 E 2 0 –2 0 0 
DownLoad: CSV
表 2 表征Fano共振特性的主要参数值
Table 2. Main parameters that characterize the resonant properties of Fano.
Parameter $ {\omega _{\text{0}}}/e{\text{V}} $ $ \Gamma /{\rm{nm}} $ F q Q $ {\lambda _{\text{1}}}= 1207.13\;{\text{nm}} $ 1.027 2.92 0.257 –1.550 413 $ {\lambda _{\text{2}}}= 1504.39\;{\text{nm}} $ 0.824 6.57 0.234 1.910 229 $ {\lambda _{\text{3}}}= 1074.80\;{\text{nm}} $ 1.154 0.26 0.221 1.536 4134 $ {\lambda _{\text{4}}} = 1093.35\;{\text{nm}} $ 1.134 0.54 0.256 1.145 2025 $ {\lambda _{\text{5}}}= 1577.74\;{\text{nm}} $ 0.786 1.11 0.285 1.413 1421
DownLoad: CSV
-
[1] 鹿利单, 祝连庆, 曾周末, 崔一平, 张东亮, 袁配 2021 70 034204
Google Scholar
Lu L D, Zhu L Q, Zeng Z M, Cui Y P, Zhang D L, Yuan P 2021 Acta Phys. Sin. 70 034204
Google Scholar
[2] Tribelsky M I, Miroshnichenko A E 2016 Phys. Rev. A 93 053837
Google Scholar
[3] Kong X H, Xiao G B 2016 J. Opt. Soc. Am. A 33 707
Google Scholar
[4] Poddubny A N, Rybin M V, Limonov M F, Kivshar Y S 2012 Nat. Commun. 3 914
Google Scholar
[5] Rybin M V, Mingaleev S F, Limonov M F, Kivshar Y S 2016 Sci. Rep. 6 20599
Google Scholar
[6] Rybin M V, Khanikaev A B, Inoue M, Samusev K B, Steel M J, Yushin G, Limonov M F 2009 Phys. Rev. Lett. 103 023901
Google Scholar
[7] Sharac, N, Sharma H, Veysi M, Sanderson R N, Khine M, Capolino F, Ragan R 2016 Nanotechnology 27 105302
Google Scholar
[8] Guo M, Huang L R, Liu W B, Ding J F 2021 Opt. Mater. 112 110802
Google Scholar
[9] Wang W D, Zheng L, Wang Y L 2020 Opt. Commun. 454 124516
Google Scholar
[10] Kong Y, Cao J J, Qian W C, Liu C, Wang S Y 2018 IEEE Photon. J. 10 1943
Google Scholar
[11] Zhang Y H, Liang Z Z, Meng D J, Qin Z, Fan Y D, Shi X Y, Smith D R, Hou E Z 2021 Results Phys. 24 104129
Google Scholar
[12] Brandl D W, Mirin N A, Nordlander P 2006 J. Phys. Chem. B 110 12302
Google Scholar
[13] Hopkins B, Poddubny A N, Miroshnichenko A E, Kivshar Y S 2013 Phys. Rev. A (Coll Park) 88 053819
Google Scholar
[14] Forestiere C, Negro L D, Miano G 2013 Phys. Rev. B 88 155411
Google Scholar
[15] Gomez D E, Vernon K C, Davis T J 2010 Phys. Rev. B 81 075414
Google Scholar
[16] Johnson P B, Christy R W 1972 Phys. Rev. B 6 4370
Google Scholar
[17] Chen Q, Wang D, Gao F 2021 Opt. Lett. 46 1209
Google Scholar
[18] Ito T, Sakoda K 2001 Phys. Rev. B 64 045117
Google Scholar
[19] Crozier K B, Lousse V, Kilic O, Kim S, Fan S, Solgaard O 2006 Phys. Rev. B 73 115126
Google Scholar
[20] 崔成聪 2020 博士学位论文 (武汉: 华中科技大学)
Cui C C 2020 Ph. D. Dissertation (Wuhang: Huazhong University of Science and Technology) (in Chinese)
[21] Kilic O, Digonnet M, Kino G, Solgaard O 2008 Opt. Express 16 13090
Google Scholar
[22] Nicolaou C, Lau W T, Gad R, Akhavan H, Schilling R, Levi O 2013 Opt. Express 21 31698
Google Scholar
[23] Fan S H 2002 Phys. Rev. B 65 235112
Google Scholar
[24] Liu S D, Yang Z, Liu R P, Li X Y 2012 ACS Nano 6 6260
Google Scholar
[25] Rajratan B, Atwood L J 2019 Opt. Express 27 282
Google Scholar
[26] Lee J, Zhen B, Chua S L, Qiu W J, Joannopoulos J D, Soljacic M, Shapira O 2012 Phys. Rev. Lett. 109 067401
Google Scholar
[27] Staude I, Schilling J 2017 Nat. Photonics 11 274
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 3907
- PDF Downloads: 112
- Cited By: 0
