-
本文设计了由不对称半圆柱对阵列组成的全介质超构表面, 获得了两个高品质因子的准连续域束缚态模式(quasi-bound states in the continuum, QBIC). 通过选择不同形式的对称破缺, 在近红外频段均可产生两个稳健的QBIC, 并且二者的谐振波长、品质因子、偏振依赖等表现出不同的特性. 模拟计算表明, 通过测量两个QBIC的谐振波长, 能够实现折射率和温度的双参数传感; 通过调节不对称参数, 利用QBIC的品质因子依赖于不对称参数的二次方反比关系, 理论上能够提高品质因子到任意的数值, 从而实现传感性能的提升和调节. 该超构表面的折射率传感灵敏度、品质因子和优值分别达到194.7 nm/RIU, 45829和8197, 其温度传感灵敏度达到24 pm/℃.
Refractive index sensors based on metal metasurfaces are commonly limited by their low quality factors due to significant Ohmic losses in the metal material. In contrast, sensors based on all-dielectric metasurfaces can overcome this disadvantage. Currently, all-dielectric metesurface sensors based on symmetry-protected bound states in the continuum (BIC) have aroused intense research interest due to their ability to achieve ultrahigh quality factors. Such a metasurface sensor is mainly based on single BIC and single form of symmetry breaking. There are few studies on metasurface sensors of multiple BICs and multiple forms of symmetry breaking. In additon, the refractive-index sensors commonly neglect the influence of temperature fluctuation and thus suffer the crosstalk between the refractive index and temperature of the environment. In this work, an all-dielectric metasurface composed of a periodic array of asymmetric semicircular-cylinder pairs is designed and two quasi-bound states in the continuum (QBIC) with high quality factors are obtained. By choosing three different forms of symmetry breaking (two in-plane and one out-of-plane), two robust QBIC modes can be generated in the selected near-infrared frequency band, and their resonance wavelengths, quality factors and polarization dependences exhibit different characteristics. Full-wave simulation results show that by measuring the resonance wavelengths of the two QBICs (denoted by QBIC1 and QBIC2), two-parameter sensing of refractive index and temperature can be achieved, which then solves the problem of crosstalk between the refractive index and temperature of the environment in refractive-index sensing. The dependence of quality factor on asymmetric parameters follows an inverse quadratic relation for the two QBICs. By adjusting the asymmetric parameters, the quality factor can be theoretially increased to any value, so that the sensing performance can be improved and adjusted. For refractive-index sensing, the QBIC1 can achieve a sensitivity of 194.7 nm/RIU and a highest figure of merit (FOM) of 8197 (corresponding to a quality factor of 45829); the QBIC2 can achieve a sensitivity of 170 nm/RIU, and a highest FOM of 4970 (corresponding to a quality factor of 28097). For temperature sensing, the QBIC1 can achieve a sensitivity of 7.77 pm/℃, and the QBIC2 can achieve a sensitivity of 24 pm/℃. -
Keywords:
- metasurface /
- quasi-bound states in the continuum /
- symmetry breaking /
- refractive index sensing /
- temperature sensing
[1] Koshelev K, Favraud G, Bogdanov A, Kivshar Y, Fratalocchi A 2019 Nanophotonics 8 725
Google Scholar
[2] Neumann J V, Wigner E P 1929 Phys. Z 30 465
[3] Hsu C W, Zhen B, Stone A D, Joannopoulos J D, Soljacic M 2016 Nat. Rev. Mater. 1 16048
Google Scholar
[4] Bulgakov E N, Sadreev A F 2008 Phys. Rev. B 78 075105
Google Scholar
[5] Plotnik Y, Peleg O, Dreisow F, Heinrich M, Nolte S, Szameit A, Segev M 2011 Phys. Rev. Lett. 107 183901
Google Scholar
[6] Li Z J, Zhu Q, Wang Y N, Xie S X 2019 Opt. Commun. 436 151
Google Scholar
[7] Romano S, Zito G, Lara Yépez S N, Cabrini S, Penzo E, Coppola G, Rendina I, Mocellaark V 2019 Opt. Express 27 18776
Google Scholar
[8] Maksimov D N, Bogdanov A A, Bulgakov E N 2020 Phys. Rev. A 102 033511
Google Scholar
[9] Kikkawa R, Nishida M, Kadoya Y 2020 New J. Phys. 22 073029
Google Scholar
[10] Chen X, Fan W H 2020 Nanomaterials (Basel) 10 623
Google Scholar
[11] Srivastava Y K, Ako R T, Gupta M, Bhaskaran M, Sriram S, Singh R 2019 Appl. Phys. Lett. 115 151105
Google Scholar
[12] Ndao A, Hsu L, Cai W, Ha J, Park J, Contractor R, Lo Y, Kanté B 2020 Nanophotonics 9 1081
Google Scholar
[13] Koshelev K, Lepeshov S, Liu M K, Bogdanov A, Kivshar Y 2018 Phys. Rev. Lett. 121 193903
Google Scholar
[14] Yin W, Shen Z L, Li S N, Cui Y Q, Gao F, Hao H B, Zhang L Y, Chen X F 2022 Opt. Express 30 32162
Google Scholar
[15] Garmon S, Nakamura H, Hatano N, Petrosky T 2009 Phys. Rev. B 80 115318
Google Scholar
[16] Jiang H, Han Z H 2022 J. Phys. D: Appl. Phys. 55 385106
[17] Han Z H, Cai Y J 2021 Opt. Lett. 46 524
Google Scholar
[18] Koshelev K, Bogdanov A, Kivshar Y 2019 Sci. Bull. 64 836
Google Scholar
[19] Liu Y H, Luo Y, Jin X Y, Zhou X, Song K, Zhao X P 2016 Plasmonics 12 1431
[20] Sun G H, Yuan L R, Zhang Y, Zhang X J, Zhu Y Y 2017 Sci. Rep. 7 8128
Google Scholar
[21] Mikheeva E, Koshelev K, Choi D Y, Kruk S, Lumeau J, Abdeddaim R, Voznyuk I, Enoch S, Kivshar Y 2019 Opt. Express 27 33847
Google Scholar
[22] Wang W D, Zheng L, Qi J G 2019 Appl. Phys. Express 12 075002
Google Scholar
[23] Modi K S, Kaur J, Sigh S P, Tiwari U, Sinha R K 2020 Opt. Commun. 462 125327
Google Scholar
[24] Ahmed A M, Elsayed H A, Mehaney A 2021 Plasmonics 16 547
Google Scholar
[25] Palik E D 1985 Handbook of Optical Constants of Solids, Part I (San Diego: Academic Press) pp565–566
[26] Zhao L, Wang J Y, Li H Y, Zhang C, Kang G G 2021 IEEE 16th International Conference on Nano/Micro Engineered and Molecular Systems (NEMS) Xiamen, China, 2021 p1441
-
图 1 (a) 半圆柱对全介质超构表面示意图; (b) 单元晶胞俯视图
Fig. 1. (a) Schematic diagram of the all-dielectric metasurface composed of semicircular cylinder pairs; (b) top view of a unit cell.
图 2 对称超构表面的透射率谱, 红色实线对应x向偏振光入射, 蓝色实线对应y向偏振光入射. 图中4个圆圈表示4个QNM本征模式复数本征波长的实部, 红色、绿色、蓝色和紫色圆圈对应的QNM分别记为Mx, BIC2, My, BIC1
Fig. 2. Transmission spectrum of the symmetric metasurface. Red solid line corresponds to the incidence of x-polarized light, the blue solid line corresponds to the incidence of y-polarized light. Circles in the figure represent the real part of the complex eigenwavelengths of the four QNM eigenmodes, and the QNMs corresponding to the red, green, blue and purple circles are denoted as Mx, BIC2, My and BIC1, respectively.
图 3 (a) 两种BIC模式在x-y平面(z = d1, z<d1一侧)的电场分布图, 白色箭头表示电场矢量方向; (b) 两种BIC模式在x-y平面(z = d1)的磁场分布图, 白色箭头表示磁场矢量方向; (c) 两种BIC模式在y-z平面(x = 0)的电场分布图; (d) 两种BIC模式在y-z平面(x = 0)的磁场分布图. 图中叠加的黑色实线显示了对称超构表面的边界, E0, H0分别表示入射平面波的电场、磁场矢量
Fig. 3. (a) Electric-field distributions of the two BIC modes in the x-y plane (z = d1, on the side of z < d1), with the white arrows indicating the direction of the electric field vector; (b) magnetic-field distributions of the two BIC modes in the x-y plane (z = d1), with the white arrows indicating the direction of the magnetic field vector; (c) electric-field distributions of the two BIC modes in the y-z plane (x = 0); (d) magnetic-field distributions of the two BIC modes in the y-z plane (x = 0). The superimposed black solid lines show the boundary of the symmetric metasurface. The E0 and H0 represent the electric-field and magnetic-field vectors of the incident plane wave, respectively.
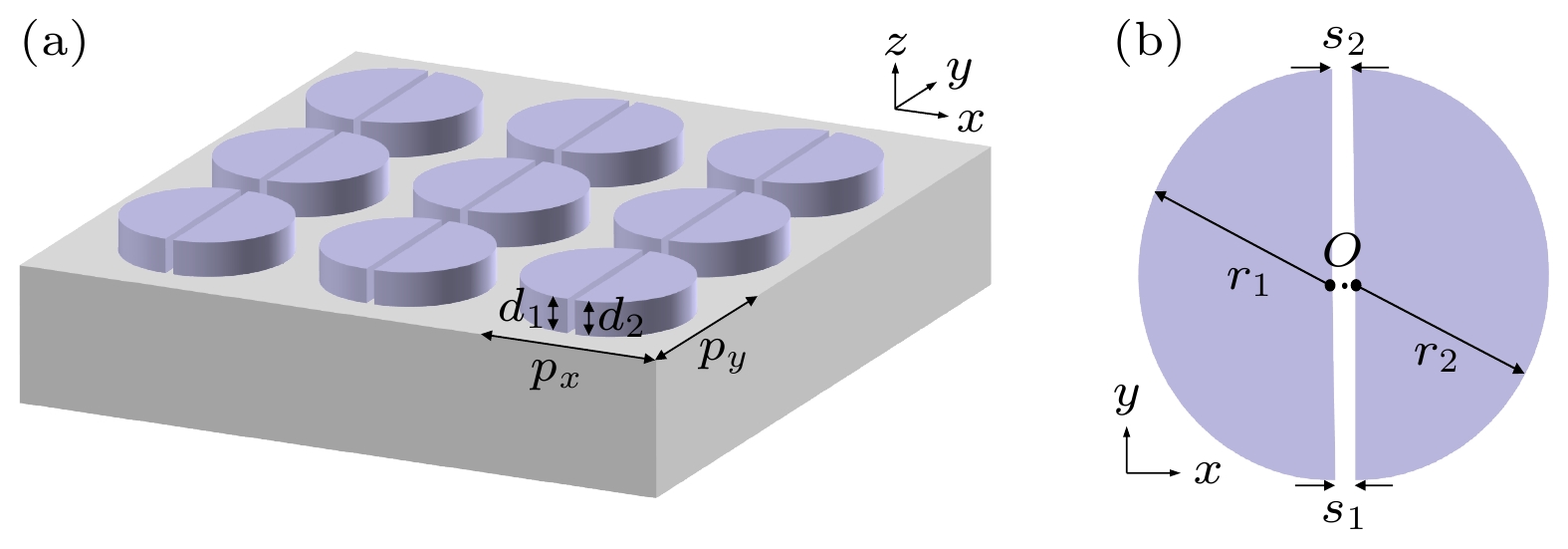
图 4 (a) 面内不对称参数$\alpha = s_2 - s_1 \neq 0 $时全介质超构表面示意图; (b) 不对称参数α不同时, x向偏振光入射对应的透射率谱线; (c) 不对称参数α不同时, 四个本征模式的Q因子变化曲线; (d) QBIC1和QBIC2的Q因子随1/α2的变化曲线
Fig. 4. (a) Schematic diagram of the all-dielectric metasurface when the in-plane asymmetric parameter $\alpha = s_2 - s_1 \neq 0$; (b) transmittance spectra for x-polarized incident light and different asymmetric parameters α; (c) Q-factors of the four eigenmodes plotted as functions of the asymmetric parameter α; (d) Q-factors of QBIC1 and QBIC2 plotted as functions of 1/α2.
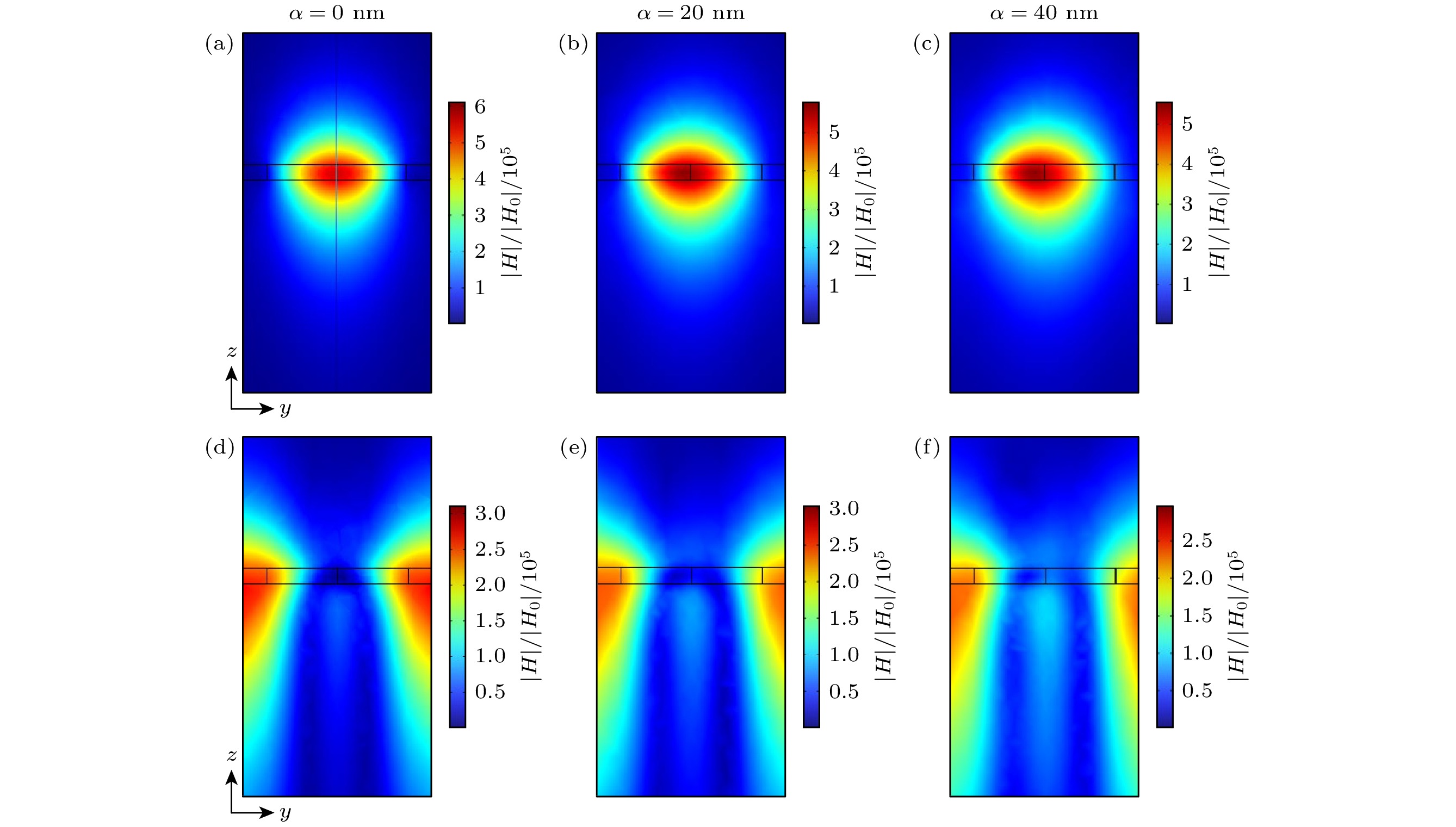
图 5 (a) α = 0 nm, (b) α = 20 nm, (c) α = 40 nm时BIC1(或QBIC1)在平面x = 0内的磁场振幅分布; (d) α = 0 nm, (e) α = 20 nm, (f) α = 40 nm时BIC2 (或QBIC2)在平面x = 0内的磁场振幅分布. 图中叠加的黑色实线显示了结构的边界, H0表示入射平面波的磁场矢量
Fig. 5. Distributions of magnetic-field amplitude for BIC1 (or QBIC1) in plane x = 0 when (a) α = 0 nm, (b) α = 20 nm, (c) α = 40 nm, and distributions of magnetic-field amplitude for BIC2 (or QBIC2) in plane x = 0 when (d) α = 0 nm, (e) α = 20 nm, (f) α = 40 nm. The superimposed black solid lines show the boundary of the structure. The H0 represents the magnetic-field vector of the incident plane wave.
图 6 (a) 面内不对称参数$\beta = r_1- r_2 \neq 0 $β = r1–r2 ≠ 0时全介质超构表面示意图; (b) 不对称参数β不同时, y向偏振光入射对应的透射率谱; (c) 不对称参数β不同时, 四个本征模式的Q因子变化曲线; (d) QBIC1和QBIC2的Q因子随1/β2的变化曲线
Fig. 6. (a) Schematic diagram of the all-dielectric metasurface when the in-plane asymmetric parameter $\beta = r_1- r_2 \neq 0 $; (b) transmittance spectra for y-polarized incident light and different asymmetric parameters β; (c) Q-factors of the four eigenmodes plotted as functions of the asymmetric parameter β; (d) Q-factors of QBIC1 and QBIC2 plotted as functions of 1/β2.
图 7 (a) 面外不对称参数$\gamma = d_2 - d_1 \neq 0 $时全介质超构表面示意图; (b) 不对称参数γ不同时, y向偏振光入射对应的透射率谱; (c) 不对称参数γ不同时, 四个本征模式的Q因子变化曲线; (d) QBIC1和QBIC2的Q因子随1/γ2的变化曲线
Fig. 7. (a) Schematic diagram of the all-dielectric metasurface when the out-of-plane asymmetric parameter $\gamma = d_2 - d_1 \neq 0 $ (b) transmittance spectra for y-polarized incident light and different asymmetric parameters γ; (c) Q-factors of the four eigenmodes plotted as functions of the asymmetric parameter γ; (d) Q-factors of QBIC1 and QBIC2 plotted as functions of 1/γ2.
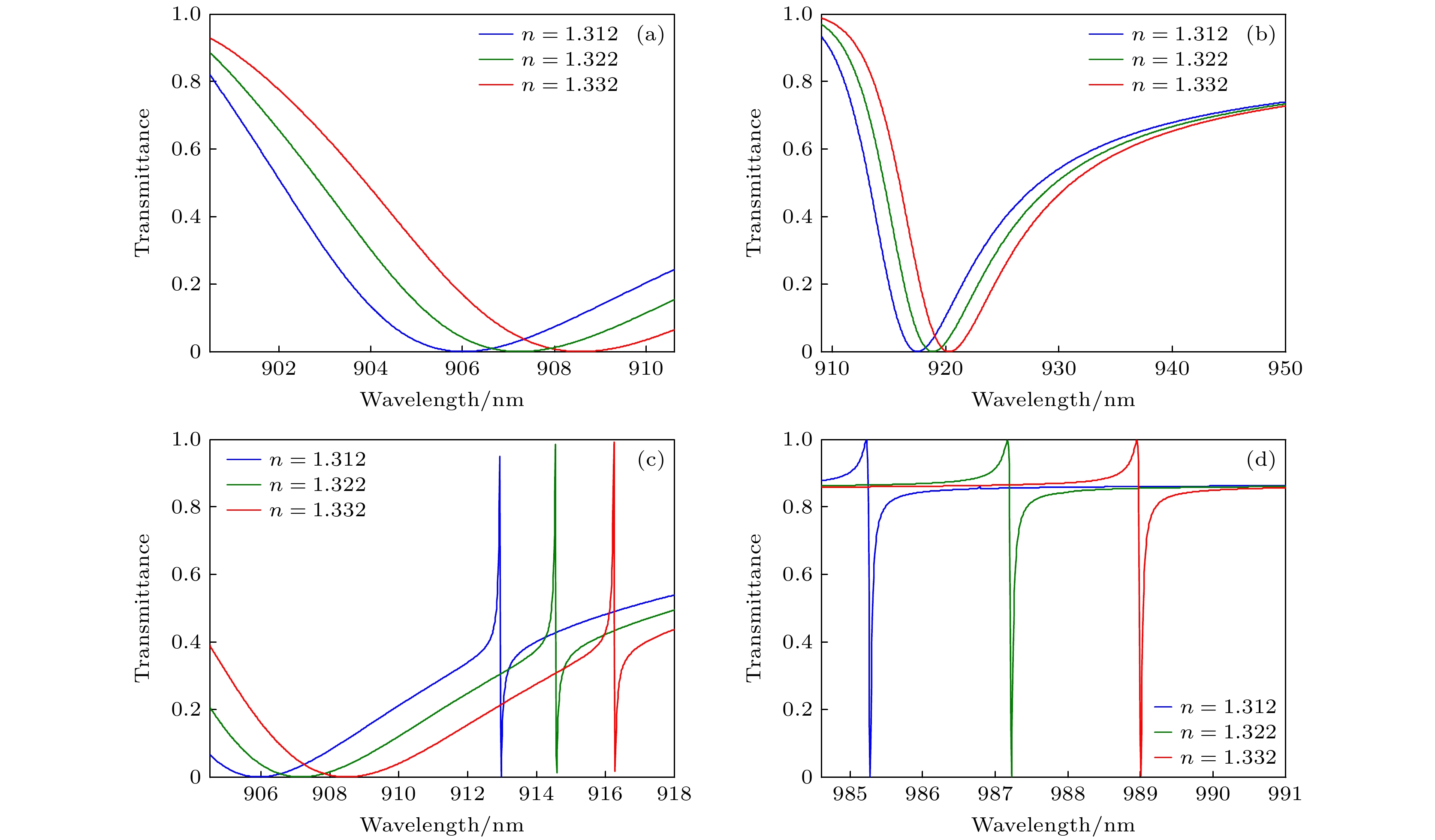
图 8 待测液体折射率n变化时, 不同模式谐振波长附近的透射率谱. 设仅引入不对称参数α = 8 nm (β = γ = 0), x偏振光入射(a) Mx; (b) My; (c) QBIC2; (d) QBIC1
Fig. 8. When the refractive index n of the tested liquid changes, the transmittance spectra of different modes. Only the asymmetric parameter α = 8 nm (β = γ = 0) is introduced, and the incident light is x-polarized: (a) Mx; (b) My; (c) QBIC2; (d) QBIC1.
图 9 (a)考虑硅材料损耗, 取波长和结构尺寸缩放因子η =1, 1.7和3时, 传感器的透射率谱; (b)当两个半圆柱的半径r1 = r2 = 223, 225和227 nm时, 传感器的透射率谱. 上述计算中, 取待测液体折射率n = 1.312
Fig. 9. (a) Transmittance spectra of the sensor with the wavelength and all geometrical sizes scaled by a factor of η =1, 1.7 and 3, and with the material loss of silicon being considered; (b) transmittance spectra of the sensor when the two semicircular cylinders’ radii are r1 = r2 = 223, 225 and 227 nm. In the calculation, the refractive index of the measured liquid is n = 1.312.
图 10 不对称参数β = 6 nm时(α = γ = 0), 不同温度T下的透射率谱曲线. 水溶液折射率n设置为1.312, y向偏振光入射
Fig. 10. Spectral curves of transmittance for different temperatures T and the asymmetric parameter β = 6 nm (α = γ = 0). The refractive index n of the aqueous solution is set to 1.312, and the incident light is y-polarized.
图 11 不对称参数β = 6 nm时(α = γ = 0), 对于不同的温度, QBIC1和QBIC2的共振波长及其线性拟合. 水溶液折射率n = 1.312, y向偏振光入射
Fig. 11. Resonance wavelengths of QBIC1 and QBIC2 at different temperatures and their linear fit when the asymmetric parameter β = 6 nm (α = γ = 0). The refractive index of the aqueous solution is n = 1.312, and the incident light is y-polarized.
表 1 不同的不对称参数下四个模式折射率传感的计算结果
Table 1. Calculation results of the four modes for refractive-index sensing with different asymmetric parameters.
不对称参数 模式 共振波长/nm 折射率传感灵敏度/(nm·RIU–1) Q FOM
α = 8 nm
(β = γ = 0)Mx 906.01 123 86 11.7 My 917.51 139.2 88 13.4 QBIC1 985.28 194.7 30125 5953 QBIC2 912.97 161.5 28097 4970
β = 6 nm
(α = γ = 0)Mx 906.08 128 83.4 11.8 My 917.45 141 80.5 12.4 QBIC1 984.01 174 45829 8197 QBIC2 911.69 160.3 6639 1143
γ = 2 nm
(α = β = 0)Mx 908.63 134 72.8 10.7 My 922.01 138 78.7 11.8 QBIC1 991.35 172 41417 7186 QBIC2 915.35 170 7572 1406 
下载: 导出CSV
表 2 不同的不对称参数对应的温度传感灵敏度的计算结果
Table 2. Calculated temperature-sensing sensitivities for different asymmetric parameters.
不对称参数 QBIC1温度传感
灵敏度/(pm·℃–1)QBIC2温度传感
灵敏度/(pm·℃–1)β = 2 nm 13.19 23.5 β = 4 nm 12.51 23.3 β = 6 nm 6.81 23.19 α = 3 nm 7.43 23.39 α = 5 nm 7.43 23.31 α = 8 nm 7.27 23.19 γ = 2 nm 7.77 24.0 γ = 3 nm 8.0 24.31 γ = 5 nm 8.27 24.69
下载: 导出CSV
表 3 对于折射率和温度双参数传感, 矩阵理论预测的结果($\Delta {n_{{\mathrm{cal}}}}$和$ \Delta {T_{{\mathrm{cal}}}} $)和设定值($\Delta {n_{{\mathrm{set}}}}$和$ \Delta {T_{{\mathrm{set}}}} $)之间的对比
Table 3. Comparison between the matrix-theory predictions ($\Delta {n_{{\mathrm{cal}}}}$ and $ \Delta {T_{{\mathrm{cal}}}} $) and the preset values ($\Delta {n_{{\mathrm{set}}}}$ and $ \Delta {T_{{\mathrm{set}}}} $) for the refractive index and temperature dual-parameter sensing.
不对称参数 $\Delta {n_{{\mathrm{set}}}}$ $ \Delta {T}_{{\mathrm{set}}}/ $℃ $\Delta {\lambda _1}/{\mathrm{nm}}$ $\Delta {\lambda _2}/{\mathrm{nm}}$ $\Delta {n_{{\mathrm{cal}}}}$ $ \Delta {T}_{{\mathrm{cal}}}/ $℃ $ {\delta _n} $ $ {\delta _T} $ β = 6 nm 0.015 20 2.52 3.06 0.0149 20.57 –0.67% 2.85% 0.02 20 3.35 3.945 0.0202 19.56 1% –2.2% 0.01 40 1.84 2.66 0.0097 41.99 –3% 4.975% 0.02 40 3.50 4.41 0.0202 38.70 1% –3.25% 0.01 60 1.99 3.12 0.00984 60.82 –1% 1.37% α = 8 nm 0.015 20 2.615 3.085 0.0148 20.758 –1.33% 3.79% 0.02 20 3.475 3.97 0.0201 19.23 0.5% –3.85% 0.01 40 1.92 2.67 0.0098 41.35 –2% 3.375% 0.02 40 3.63 4.43 0.0202 38.33 1% –4.175% 0.01 60 2.07 3.13 0.00981 60.79 –1.9% 1.317% γ = 2 nm 0.015 20 2.72 3.08 0.01482 20.90 –1.2% 4.5% 0.02 20 3.61 3.96 0.020 19.84 0% –0.8% 0.01 40 2.01 2.69 0.0098 41.05 –2% 2.625% 0.02 40 3.78 4.44 0.0201 38.93 1% –2.675% 0.01 60 2.17 3.17 0.00984 60.76 –1.6% 1.27%
下载: 导出CSV
-
[1] Koshelev K, Favraud G, Bogdanov A, Kivshar Y, Fratalocchi A 2019 Nanophotonics 8 725
Google Scholar
[2] Neumann J V, Wigner E P 1929 Phys. Z 30 465
[3] Hsu C W, Zhen B, Stone A D, Joannopoulos J D, Soljacic M 2016 Nat. Rev. Mater. 1 16048
Google Scholar
[4] Bulgakov E N, Sadreev A F 2008 Phys. Rev. B 78 075105
Google Scholar
[5] Plotnik Y, Peleg O, Dreisow F, Heinrich M, Nolte S, Szameit A, Segev M 2011 Phys. Rev. Lett. 107 183901
Google Scholar
[6] Li Z J, Zhu Q, Wang Y N, Xie S X 2019 Opt. Commun. 436 151
Google Scholar
[7] Romano S, Zito G, Lara Yépez S N, Cabrini S, Penzo E, Coppola G, Rendina I, Mocellaark V 2019 Opt. Express 27 18776
Google Scholar
[8] Maksimov D N, Bogdanov A A, Bulgakov E N 2020 Phys. Rev. A 102 033511
Google Scholar
[9] Kikkawa R, Nishida M, Kadoya Y 2020 New J. Phys. 22 073029
Google Scholar
[10] Chen X, Fan W H 2020 Nanomaterials (Basel) 10 623
Google Scholar
[11] Srivastava Y K, Ako R T, Gupta M, Bhaskaran M, Sriram S, Singh R 2019 Appl. Phys. Lett. 115 151105
Google Scholar
[12] Ndao A, Hsu L, Cai W, Ha J, Park J, Contractor R, Lo Y, Kanté B 2020 Nanophotonics 9 1081
Google Scholar
[13] Koshelev K, Lepeshov S, Liu M K, Bogdanov A, Kivshar Y 2018 Phys. Rev. Lett. 121 193903
Google Scholar
[14] Yin W, Shen Z L, Li S N, Cui Y Q, Gao F, Hao H B, Zhang L Y, Chen X F 2022 Opt. Express 30 32162
Google Scholar
[15] Garmon S, Nakamura H, Hatano N, Petrosky T 2009 Phys. Rev. B 80 115318
Google Scholar
[16] Jiang H, Han Z H 2022 J. Phys. D: Appl. Phys. 55 385106
[17] Han Z H, Cai Y J 2021 Opt. Lett. 46 524
Google Scholar
[18] Koshelev K, Bogdanov A, Kivshar Y 2019 Sci. Bull. 64 836
Google Scholar
[19] Liu Y H, Luo Y, Jin X Y, Zhou X, Song K, Zhao X P 2016 Plasmonics 12 1431
[20] Sun G H, Yuan L R, Zhang Y, Zhang X J, Zhu Y Y 2017 Sci. Rep. 7 8128
Google Scholar
[21] Mikheeva E, Koshelev K, Choi D Y, Kruk S, Lumeau J, Abdeddaim R, Voznyuk I, Enoch S, Kivshar Y 2019 Opt. Express 27 33847
Google Scholar
[22] Wang W D, Zheng L, Qi J G 2019 Appl. Phys. Express 12 075002
Google Scholar
[23] Modi K S, Kaur J, Sigh S P, Tiwari U, Sinha R K 2020 Opt. Commun. 462 125327
Google Scholar
[24] Ahmed A M, Elsayed H A, Mehaney A 2021 Plasmonics 16 547
Google Scholar
[25] Palik E D 1985 Handbook of Optical Constants of Solids, Part I (San Diego: Academic Press) pp565–566
[26] Zhao L, Wang J Y, Li H Y, Zhang C, Kang G G 2021 IEEE 16th International Conference on Nano/Micro Engineered and Molecular Systems (NEMS) Xiamen, China, 2021 p1441
下载:
计量
- 文章访问数: 2565
- PDF下载量: 107
- 被引次数: 0
