-
Continuous variable quantum teleportation (CVQT) plays an important role in practical quantum communication. However, the noise and loss in the actual environment will lead to the degradation of entanglement, which has an effect on the performance of the system in terms of the transmission distance and hence hinders its implementations. In this paper, we suggest an approach to improving the performance of the CVQT system with an embedded noiseless linear amplifier (NLA). By using the NLA, one can amplify the degenerated entangled source to compensate for the attenuation of the fiber. Then we consider the influences of the available gains of the NLA on the performance of the proposed scheme under different lossy channels and entangled sources. The simulation results show that the performance is improved in fidelity and transmission distance, which may provide a feasible and effective method of putting the long-distance CVQT into practical application .
[1] Bennett C H, Brassard G, Crépeau C, Jozsa R, Peres A, Wootters W K 1993 Phys. Rev. Lett. 70 1895
Google Scholar
[2] Bouwmeester D, Pan J W, Mattle K, Eibl M, Weinfurter H, Zeilinger A 1997 Nature 390 575
Google Scholar
[3] Hu X M, Zhang C, Liu B H, Cai Y, Ye X J, Guo Y, Xing W B, Huang C X, Huang Y F, Li C F, Guo G C 2020 Phys. Rev. Lett. 125 230501
Google Scholar
[4] Braunstein S L, Kimble H J 1998 Phys. Rev. Lett. 80 869
Google Scholar
[5] Lee N, Benichi H, Takeno Y, Takeda S, Webb J, Huntington E, Furusawa A 2011 Science 332 330
Google Scholar
[6] Huo M R, Qin J L, Cheng J L, Yan Z H, Qin Z Z, Su X L, Jia X J, Xie C D, Peng K C 2018 Sci. Adv. 4 eaas9401
Google Scholar
[7] Marcikic I, De Riedmatten H, Tittel W, Zbinden H, Gisin N 2003 Nature 421 509
Google Scholar
[8] Yin J, Ren J G, Lu H, Cao Y, Yong H L, Wu Y P, Liu C, Liao S K, Zhou F, Jiang Y, Cai X D, Xu P, Pan G S, Jia J J, Huang Y M, Yin H, Wang J Y, Chen Y A, Peng C Z, Pan J W 2012 Nature 488 185
Google Scholar
[9] Ren J G, Xu P, Yong H L, Zhang L, Liao S K, Yin J, Liu W Y, Cai W Q, Yang M, Li L, Yang K X, Han X, Yao Y Q, Li J, Wu H Y, Wan S, Liu L, Liu D Q, Kuang Y W, He Z P, Shang P, Guo C, Zheng R H, Tian K, Zhu Z C, Liu N L, Lu C Y, Shu R, Chen Y A, Peng C Z, Wang J Y, Pan J W 2017 Nature 549 70
Google Scholar
[10] Vaidman L 1994 Phys. Rev. A 49 1473
Google Scholar
[11] Ralph T C, Lam P K 1998 Phys. Rev. Lett. 81 5668
Google Scholar
[12] Furusawa A, Sørensen J L, Braunstein S L, Fuchs C A, Kimble H J, Polzik E S 1998 Science 282 706
Google Scholar
[13] Bowen W P, Treps N, Buchler B C, Schnabel R, Ralph T C, Bachor H A, Symul T, Lam P K 2003 Phys. Rev. A 67 032302
Google Scholar
[14] Zhang T C, Goh K W, Chou C W, Lodahl P, Kimble H J 2003 Phys. Rev. A 67 033802
Google Scholar
[15] Takei N, Aoki T, Koike S, Yoshino K I, Wakui K, Yonezawa H, Hiraoka T, Mizuno J, Takeoka M, Ban M, Furusawa A 2005 Phys. Rev. A 72 042304
Google Scholar
[16] Takei N, Yonezawa H, Aoki T, Furusawa A 2005 Phys. Rev. Lett. 94 220502
Google Scholar
[17] Dell’Anno F, De Siena S, Albano L, Illuminati F 2007 Phys. Rev. A 76 022301
Google Scholar
[18] Dell’Anno F, De Siena S, Illuminati F 2010 Phys. Rev. A 81 012333
Google Scholar
[19] He G Q, Zhang J T, Zhu J, Zeng G H 2011 Phys. Rev. A 84 034305
Google Scholar
[20] Hu L Y, Liao Z Y, Ma S L, Zubairy M S 2016 Phys. Rev. A 93 033807
Google Scholar
[21] Hofmann K, Semenov A A, Vogel W, Bohmann M 2019 Phys. Scr. 94 125104
Google Scholar
[22] Zuo Z Y, Wang Y J, Liao Q, Guo Y 2021 Phys. Rev. A 104 022615
Google Scholar
[23] Villaseñor E, He M J, Wang Z Q, Malaney R, Win M Z 2021 IEEE Trans. Quantum Eng. 2 4102118
Google Scholar
[24] Liu S H, Lou Y B, Jing J T 2020 Nat. Commun. 11 3875
[25] Chen X, Ou Z Y 2020 Phys. Rev. A 102 032407
Google Scholar
[26] Asjad M, Qasymeh M, Eleuch H 2021 Phys. Rev. Appl. 16 034046
Google Scholar
[27] Fedorov K G, Renger M, Pogorzalek S, Di Candia R, Chen Q M, Nojiri Y, Inomata K, Nakamura Y, Partanen M, Marx A, Gross R, Deppe F 2021 Sci. Adv. 7 eabk0891
Google Scholar
[28] Zhao H, Feng J X, Sun J K, Li Y J, Zhang K S 2022 Opt. Express 30 3770
Google Scholar
[29] Braunstein S L, Fuchs C A, Kimble H J 2000 J. Mod. Opt. 47 267
Google Scholar
[30] Fiurášek J 2002 Phys. Rev. A 66 012304
Google Scholar
[31] Blandino R, Leverrier A, Barbieri M, Etesse J, Grangier P, Tualle-Brouri R 2012 Phys. Rev. A 86 012327
Google Scholar
[32] Bai D B, Huang P, Ma H X, Wang T, Zeng G H 2017 Entropy 19 546
Google Scholar
[33] Zhang Y C, Li Z Y, Weedbrook C, Marshall K, Pirandola S, Yu S, Guo H 2015 Entropy 17 4547
Google Scholar
[34] Bohmann M, Semenov A A, Sperling J, Vogel W 2001 Phys. Rev. A 94 010302
[35] Braunstein S L, Fuchs C A, Kimble H J, van Loock P 2001 Phys. Rev. A 64 022321
-
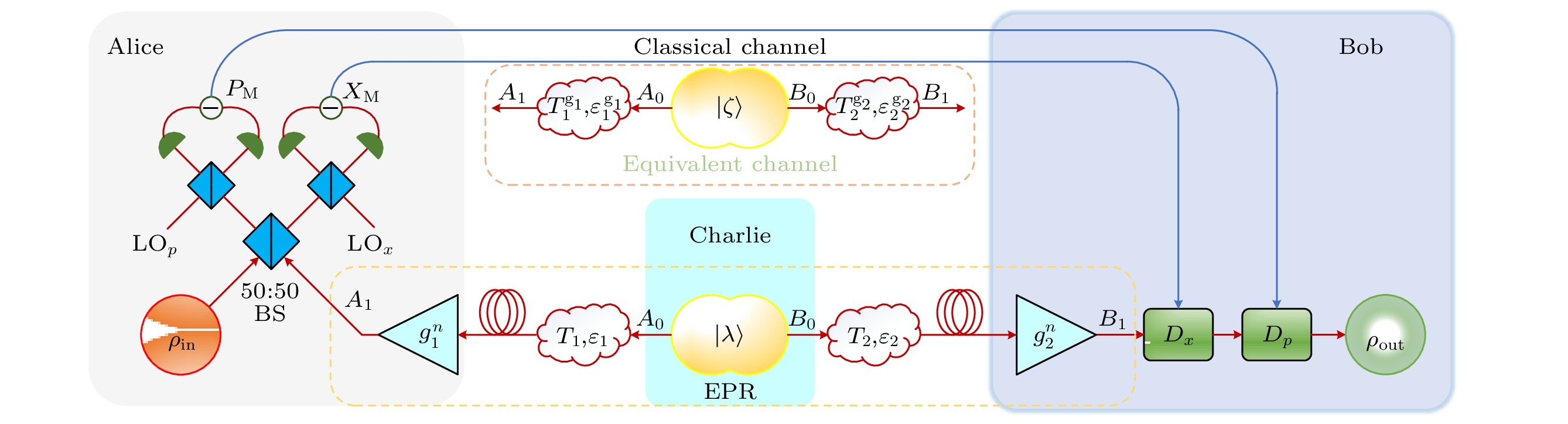
图 1 无噪线性放大CVQT方案示意图. 纠缠源EPR态由第三方Charlie制备, 模A0和B0分别经过光纤损耗信道传输至Alice和Bob端, Alice和Bob利用无噪线性放大器对接收模进行放大. LO, 本振光; BS, 分束器; g, 无噪线性放大器增益系数
Figure 1. Schematic of the NLA-based CVQT scheme. The entangled source EPR state is prepared by the third party Charlie. The modes A0 and B0 are transmitted to Alice and Bob through the fiber lossy channel. At the receiver , Alice and Bob use noiseless linear amplifiers for performance improvement. LO, local oscillator; BS, beam splitter; g, gain of NLA.
图 2 不同损耗信道中NLA增益系数随传输距离的变化关系
Figure 2. The gain coefficient of NLA versus the transmission distance in different lossy channels.
图 3 单边损耗信道情况下保真度随传输距离的变化关系 (a) EPR态参数
$ \lambda =0.5 $ , 对应NLA增益系数$ g\in \left\{2.3, 2.0, 1.7\right\} $ ; (b) EPR态参数$ \lambda =0.7 $ , 对应NLA增益系数$ g\in \left\{1.5, 1.3, 1.1\right\} $ Figure 3. The fidelity versus the transmission distance in single lossy channel case: (a) The EPR parameter
$ \lambda =0.5 $ , the gain of NLA$ g\in \left\{2.3, 2.0, 1.7\right\} $ ; (b) the EPR parameter$ \lambda =0.7 $ , the gain of NLA$ g\in \left\{1.5, 1.3, 1.1\right\} $ .
图 4 对称损耗信道情况下保真度随传输距离的变化关系 (a) EPR态参数
$ \lambda =0.5 $ , 对应NLA增益系数$ g\in \left\{1.8, 1.5, 1.2\right\} $ ; (b) EPR态参数$ \lambda =0.7 $ , 对应NLA增益系数$ g\in \left\{1.4, 1.3, 1.2\right\} $ .Figure 4. The fidelity versus the transmission distance in symmetrical lossy channel case: (a) The EPR parameter
$ \lambda =0.5 $ , the gain of NLA$ g\in \left\{1.8, 1.5, 1.2\right\} $ ; (b) the EPR parameter$ \lambda =0.7 $ , the gain of NLA$ g\in \left\{1.4, 1.3, 1.2\right\} $ .
图 5 对称损耗信道情况下输入态与输出态的特征函数分布 (a) 输入态特征函数; (b) NLA方案输出态特征函数; (c) 原始方案输出态特征函数; (d) 输入态与输出态的特征函数关于X-P平面投影
Figure 5. Characteristic functions of input state and output state in symmetrical lossy channel case: (a) Characteristic function of input state; (b) characteristic function of output state with NLA; (c) characteristic function of output state without NLA; (d) projection of characteristic functions of input state and output state on X-P plane.
-
[1] Bennett C H, Brassard G, Crépeau C, Jozsa R, Peres A, Wootters W K 1993 Phys. Rev. Lett. 70 1895
Google Scholar
[2] Bouwmeester D, Pan J W, Mattle K, Eibl M, Weinfurter H, Zeilinger A 1997 Nature 390 575
Google Scholar
[3] Hu X M, Zhang C, Liu B H, Cai Y, Ye X J, Guo Y, Xing W B, Huang C X, Huang Y F, Li C F, Guo G C 2020 Phys. Rev. Lett. 125 230501
Google Scholar
[4] Braunstein S L, Kimble H J 1998 Phys. Rev. Lett. 80 869
Google Scholar
[5] Lee N, Benichi H, Takeno Y, Takeda S, Webb J, Huntington E, Furusawa A 2011 Science 332 330
Google Scholar
[6] Huo M R, Qin J L, Cheng J L, Yan Z H, Qin Z Z, Su X L, Jia X J, Xie C D, Peng K C 2018 Sci. Adv. 4 eaas9401
Google Scholar
[7] Marcikic I, De Riedmatten H, Tittel W, Zbinden H, Gisin N 2003 Nature 421 509
Google Scholar
[8] Yin J, Ren J G, Lu H, Cao Y, Yong H L, Wu Y P, Liu C, Liao S K, Zhou F, Jiang Y, Cai X D, Xu P, Pan G S, Jia J J, Huang Y M, Yin H, Wang J Y, Chen Y A, Peng C Z, Pan J W 2012 Nature 488 185
Google Scholar
[9] Ren J G, Xu P, Yong H L, Zhang L, Liao S K, Yin J, Liu W Y, Cai W Q, Yang M, Li L, Yang K X, Han X, Yao Y Q, Li J, Wu H Y, Wan S, Liu L, Liu D Q, Kuang Y W, He Z P, Shang P, Guo C, Zheng R H, Tian K, Zhu Z C, Liu N L, Lu C Y, Shu R, Chen Y A, Peng C Z, Wang J Y, Pan J W 2017 Nature 549 70
Google Scholar
[10] Vaidman L 1994 Phys. Rev. A 49 1473
Google Scholar
[11] Ralph T C, Lam P K 1998 Phys. Rev. Lett. 81 5668
Google Scholar
[12] Furusawa A, Sørensen J L, Braunstein S L, Fuchs C A, Kimble H J, Polzik E S 1998 Science 282 706
Google Scholar
[13] Bowen W P, Treps N, Buchler B C, Schnabel R, Ralph T C, Bachor H A, Symul T, Lam P K 2003 Phys. Rev. A 67 032302
Google Scholar
[14] Zhang T C, Goh K W, Chou C W, Lodahl P, Kimble H J 2003 Phys. Rev. A 67 033802
Google Scholar
[15] Takei N, Aoki T, Koike S, Yoshino K I, Wakui K, Yonezawa H, Hiraoka T, Mizuno J, Takeoka M, Ban M, Furusawa A 2005 Phys. Rev. A 72 042304
Google Scholar
[16] Takei N, Yonezawa H, Aoki T, Furusawa A 2005 Phys. Rev. Lett. 94 220502
Google Scholar
[17] Dell’Anno F, De Siena S, Albano L, Illuminati F 2007 Phys. Rev. A 76 022301
Google Scholar
[18] Dell’Anno F, De Siena S, Illuminati F 2010 Phys. Rev. A 81 012333
Google Scholar
[19] He G Q, Zhang J T, Zhu J, Zeng G H 2011 Phys. Rev. A 84 034305
Google Scholar
[20] Hu L Y, Liao Z Y, Ma S L, Zubairy M S 2016 Phys. Rev. A 93 033807
Google Scholar
[21] Hofmann K, Semenov A A, Vogel W, Bohmann M 2019 Phys. Scr. 94 125104
Google Scholar
[22] Zuo Z Y, Wang Y J, Liao Q, Guo Y 2021 Phys. Rev. A 104 022615
Google Scholar
[23] Villaseñor E, He M J, Wang Z Q, Malaney R, Win M Z 2021 IEEE Trans. Quantum Eng. 2 4102118
Google Scholar
[24] Liu S H, Lou Y B, Jing J T 2020 Nat. Commun. 11 3875
[25] Chen X, Ou Z Y 2020 Phys. Rev. A 102 032407
Google Scholar
[26] Asjad M, Qasymeh M, Eleuch H 2021 Phys. Rev. Appl. 16 034046
Google Scholar
[27] Fedorov K G, Renger M, Pogorzalek S, Di Candia R, Chen Q M, Nojiri Y, Inomata K, Nakamura Y, Partanen M, Marx A, Gross R, Deppe F 2021 Sci. Adv. 7 eabk0891
Google Scholar
[28] Zhao H, Feng J X, Sun J K, Li Y J, Zhang K S 2022 Opt. Express 30 3770
Google Scholar
[29] Braunstein S L, Fuchs C A, Kimble H J 2000 J. Mod. Opt. 47 267
Google Scholar
[30] Fiurášek J 2002 Phys. Rev. A 66 012304
Google Scholar
[31] Blandino R, Leverrier A, Barbieri M, Etesse J, Grangier P, Tualle-Brouri R 2012 Phys. Rev. A 86 012327
Google Scholar
[32] Bai D B, Huang P, Ma H X, Wang T, Zeng G H 2017 Entropy 19 546
Google Scholar
[33] Zhang Y C, Li Z Y, Weedbrook C, Marshall K, Pirandola S, Yu S, Guo H 2015 Entropy 17 4547
Google Scholar
[34] Bohmann M, Semenov A A, Sperling J, Vogel W 2001 Phys. Rev. A 94 010302
[35] Braunstein S L, Fuchs C A, Kimble H J, van Loock P 2001 Phys. Rev. A 64 022321
DownLoad:
Catalog
Metrics
- Abstract views: 4252
- PDF Downloads: 88
- Cited By: 0
