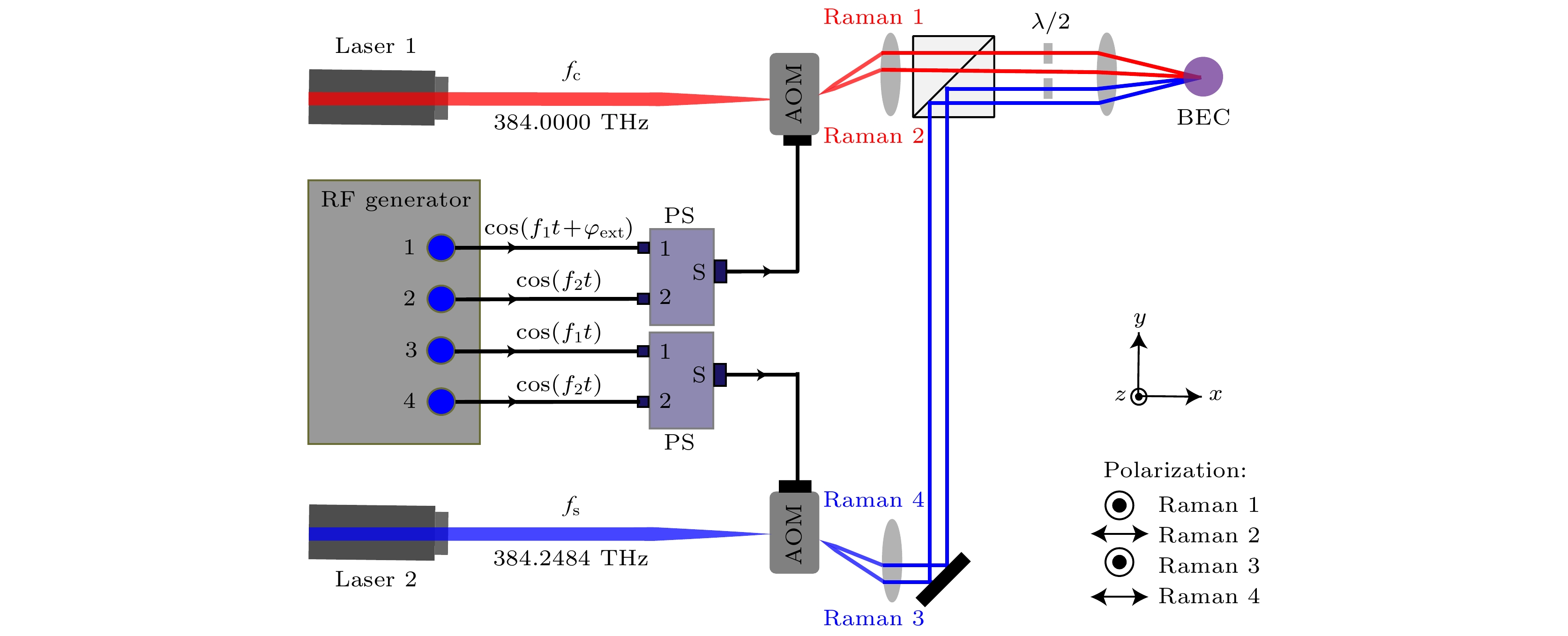
-
In this paper, we develop a new method to adjust the Raman coupling strength by using the relative phase between two pairs of Raman lasers. The stimulated Raman transition process is highly controllable and has the characteristics of multiple degrees of freedom. In experiments on ultracold atoms, the populations of atomic energy levels can be adjusted by taking an appropriate Raman light intensity and interaction time, and by detuning the two-photon frequency. The intensity of the Raman laser is usually changed to adjust the Raman coupling strength. Based on two-level atoms, a new method of accurately controlling the Raman coupling strength by using the relative phase between two pairs of Raman light beams is developed. This technology can achieve coherent manipulation of atomic quantum states, which greatly broadens the ability of ultracold atoms to perform quantum simulations. First, the 87Rb Bose-Einstein condensate is realized by using an optical dipole trap. Then, the two pairs of Raman lasers are designed with a special optical path to keep the relative phase of the two pairs of Raman lasers stable in the transmission process, and can be controlled accurately. Then the two pairs of Raman light beams act on the two ground state hyperfine energy levels
$ |1, 1\rangle $ and$ |1, 0\rangle $ of the 87Rb atom. In the experiment, we observe the relation between the percentage of atoms in the two quantum states and the relative phase between the two pairs of Raman light beams. This method provides a unique control parameter for ultracold atom quantum simulation experiments, which is the laser phase. It is hoped that this technology can be used to manipulate the interaction between light and atoms in the future to achieve more abundant physical phenomena.-
Keywords:
- stimulated Raman transition /
- laser phase /
- Raman coupling strength /
- three-level atomic system
[1] Gaubatz U, Rudecki P, Schiemann S, Bergmann K 1990 J. Chem. Phys. 92 5363
Google Scholar
[2] Vitanov N V, Rangelov A A, Shore B W, Bergmann K 2017 Rev. Mod. Phys. 89 015006
Google Scholar
[3] Kasevich M, Chu S 1992 Appl. Phys. B 54 321
Google Scholar
[4] Kasevich M, Chu S 1991 Phys. Rev. Lett. 67 181
Google Scholar
[5] Kasevich M, Chu S 1992 Phys. Rev. Lett. 69 1741
Google Scholar
[6] Davidson N, Lee H J, Kasevich M, Chu S 1994 Phys. Rev. Lett. 72 3158
Google Scholar
[7] Boyer V, Lising L J, Rolston S L, Phillips W D 2004 Phys. Rev. A 70 043405
Google Scholar
[8] Reichel J, Morice O, Tino G M, Salomon C 1994 Europhys. Lett. 28 477
Google Scholar
[9] Law C K, Eberly J H 1998 Opt. Express 2 368
Google Scholar
[10] Paparelle I, Moro L, Prati E 2020 Phys. Lett. A 384 126266
Google Scholar
[11] Ringot J, Szriftgiser P, Garreau J C 2001 Phys. Rev. A 65 013403
Google Scholar
[12] Thomas J E, Hemmer P R, Ezekiel S, Leiby C C, Picard R H, Willis C R 1982 Phys. Rev. Lett. 48 867
Google Scholar
[13] Xu Z X, Wu Y L, Tian L, Chen L R, Zhang Z Y, Yan Z H, Li S J, Wang H, Xie C D, Peng K C 2013 Phys. Rev. Lett. 111 240503
Google Scholar
[14] Král P, Shapiro M 2001 Phys. Rev. Lett. 87 183002
Google Scholar
[15] Thanopulos I, Král P, Shapiro M 2003 J. Chem. Phys. 119 5105
Google Scholar
[16] Fu Z K, Wang P J, Chai S J, Huang L H, Zhang J 2011 Phys. Rev. A 84 043609
Google Scholar
[17] Lin Y J, Compton R L, Perry A R, Phillips W D, Porto J V, Spielman I B 2009 Phys. Rev. Lett. 102 130401
Google Scholar
[18] Spielman I B 2009 Phys. Rev. A 79 063613
Google Scholar
[19] Lin Y J, Compton R L, Jiménez-García K, Porto J V, Spielman I B 2009 Nature 462 628
Google Scholar
[20] Lin Y J, Jiménez-García K, Spielman I B 2011 Nature 471 83
Google Scholar
[21] Wang P J, Yu Z Q, Fu Z K, Miao J, Huang L H, Chai S J, Zhai H, Zhang J 2012 Phys. Rev. Lett. 109 095301
Google Scholar
[22] Huang L H, Meng Z M, Wang P J, Peng P, Zhang S L, Chen L C, Li D H, Zhou Q, Zhang J 2016 Nat. Phys. 12 540
Google Scholar
[23] Ozawa T, Price H M 2019 Nat. Rev. Phys. 1 349
Google Scholar
[24] Meng Z M, Huang L H, Peng P, Li D H, Chen L C, Xu Y, Zhang C W, Wang P J, Zhang J 2016 Phys. Rev. Lett. 117 235304
Google Scholar
[25] Wu Z, Zhang L, Sun W, Xu X T, Wang B Z, Ji S C, Deng Y J, Chen S, Liu X J, Pan J W 2016 Science 354 83
Google Scholar
[26] Zhang D F, Gao T Y, Zou P, Kong L G, Li R Z, Shen X, Chen X L, Peng S G, Zhan M S, Pu H, Jiang K J 2019 Phys. Rev. Lett. 122 110402
Google Scholar
[27] Zhai H 2012 Int. J. Mod. Phys. B 26 1230001
Google Scholar
-
图 1 (a)单受激拉曼跃迁过程; (b)双受激拉曼跃迁过程
Figure 1. (a) Energy levels and stimulated Raman transitions by using two Raman lasers; (b) energy levels and double stimulated Raman transitions by using four Raman lasers.
图 2 原子在
$\left| {{g_2}} \right\rangle $ 态的布居数分布与拉曼光相位差的关系 (a)单受激拉曼过程; (b)双受激拉曼过程Figure 2. Relationship between the population in
$\left| {{g_2}} \right\rangle $ and the phase difference of Raman laser: (a) Single stimulated Raman transitions; (b) double stimulated Raman transitions.
图 3 实验光路图
Figure 3. Experimental optical diagram.
图 4 三能级87Rb原子系统中的拉曼跃迁示意图
Figure 4. Schematic diagram of Raman transitions in three level 87Rb atomic system.
图 5 量子态
$ \left| {{\rm{1}}, {\rm{0}}} \right\rangle $ 的布居数随一对拉曼光之间的相位差的关系图Figure 5. Measure the population in
$ \left| {{\rm{1}}, {\rm{0}}} \right\rangle $ as a function of phase difference of two Raman lasers.
图 6 实验测量量子态
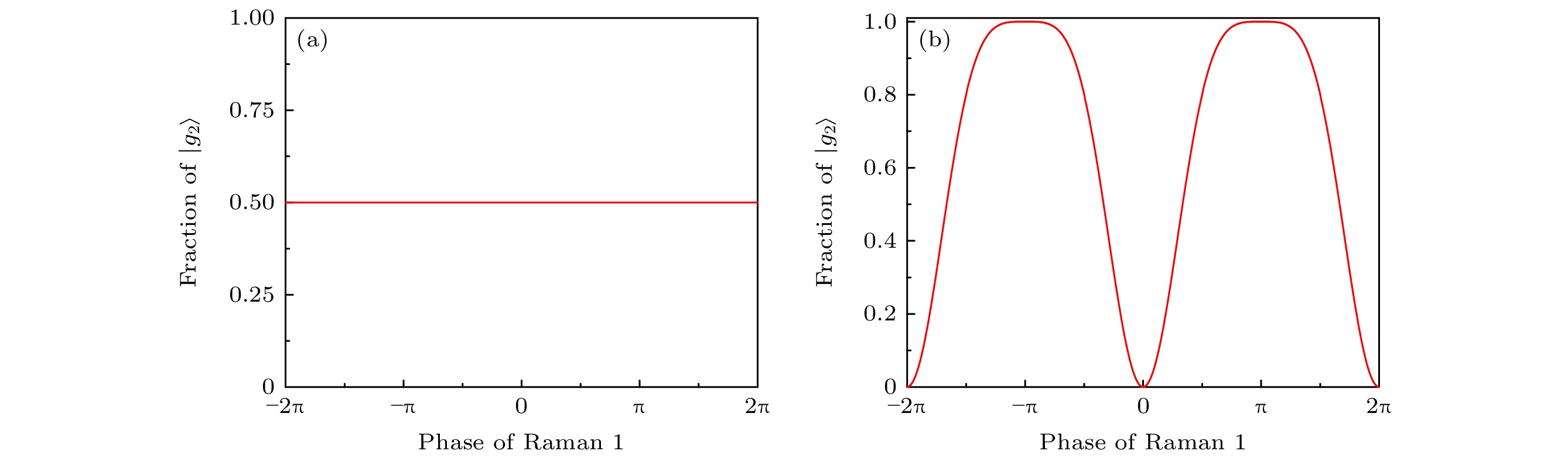
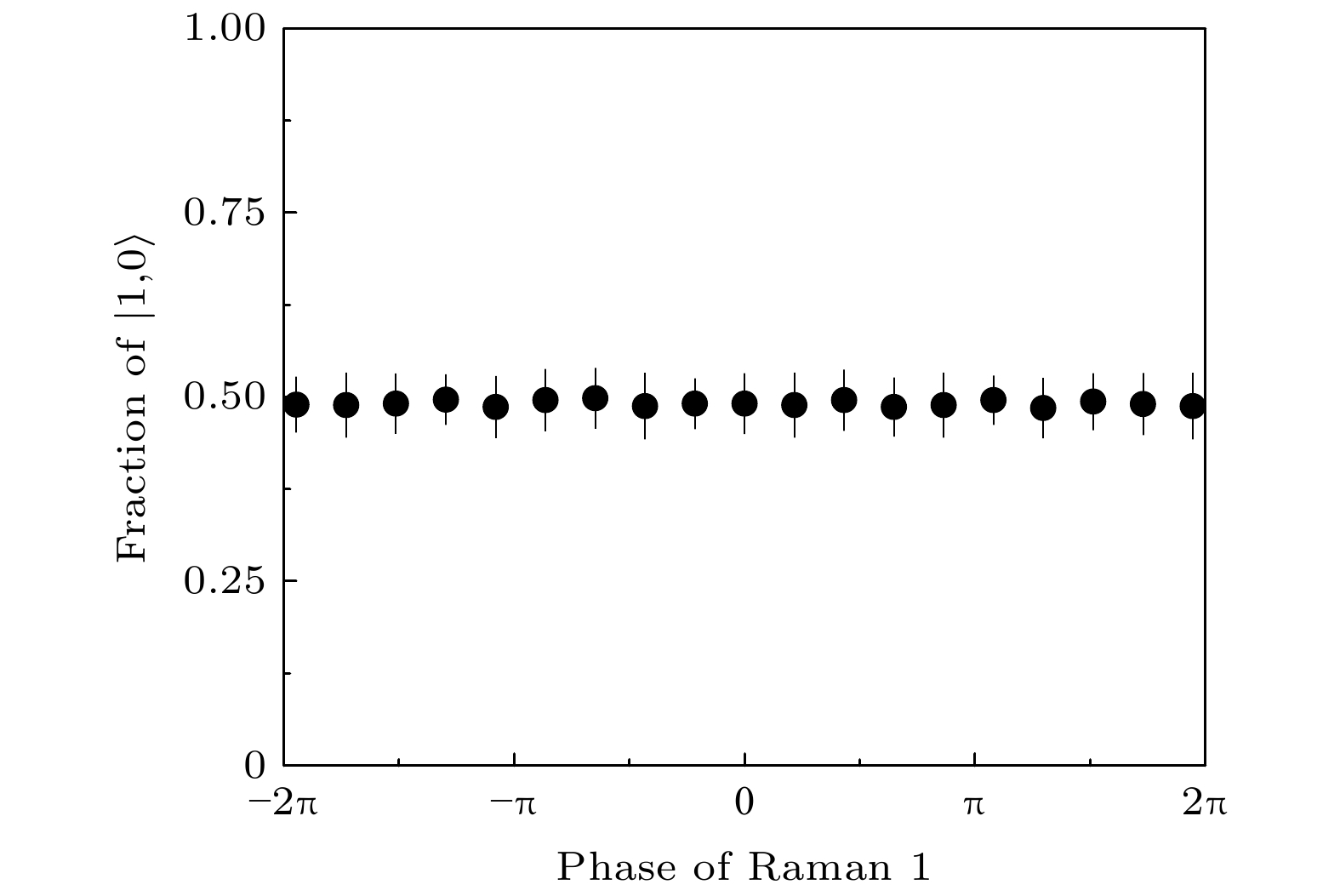
$ \left| {{\rm{1}}, {\rm{0}}} \right\rangle $ 的布居数随两对拉曼光间的相对相位的变化关系. 红色实线使用的钛宝石激光器1, 2输出频率分别为:$ {f}_{\mathrm{C}}=384.0000\;\mathrm{T}\mathrm{H}\mathrm{z} $ ,$ {f}_{\mathrm{S}}=384.2484\;\mathrm{T}\mathrm{H}\mathrm{z} $ , 红色虚线为理论计算图. 蓝色实线使用的钛宝石激光器1, 2输出频率分别为:$ {f}_{\mathrm{C}}=383.7652\;\mathrm{T}\mathrm{H}\mathrm{z} $ ,$ {f}_{\mathrm{S}}=384.2484\;\mathrm{T}\mathrm{H}\mathrm{z} $ , 蓝色虚线为理论计算图Figure 6. Measure the population in
$ \left| {{\rm{1}}, {\rm{0}}} \right\rangle $ as a function of phase of four Raman lasers. The red solid line:$ {f}_{\mathrm{C}}=384.0000\;\mathrm{T}\mathrm{H}\mathrm{z} $ ,$ {f}_{\mathrm{S}}=384.2484\;\mathrm{T}\mathrm{H}\mathrm{z} $ . The blue solid line:$ {f}_{\mathrm{C}}=383.7652\;\mathrm{T}\mathrm{H}\mathrm{z} $ ,$ {f}_{\mathrm{S}}=384.2484\;\mathrm{T}\mathrm{H}\mathrm{z} $ . The red and blue dotted line is the theoretical diagram. -
[1] Gaubatz U, Rudecki P, Schiemann S, Bergmann K 1990 J. Chem. Phys. 92 5363
Google Scholar
[2] Vitanov N V, Rangelov A A, Shore B W, Bergmann K 2017 Rev. Mod. Phys. 89 015006
Google Scholar
[3] Kasevich M, Chu S 1992 Appl. Phys. B 54 321
Google Scholar
[4] Kasevich M, Chu S 1991 Phys. Rev. Lett. 67 181
Google Scholar
[5] Kasevich M, Chu S 1992 Phys. Rev. Lett. 69 1741
Google Scholar
[6] Davidson N, Lee H J, Kasevich M, Chu S 1994 Phys. Rev. Lett. 72 3158
Google Scholar
[7] Boyer V, Lising L J, Rolston S L, Phillips W D 2004 Phys. Rev. A 70 043405
Google Scholar
[8] Reichel J, Morice O, Tino G M, Salomon C 1994 Europhys. Lett. 28 477
Google Scholar
[9] Law C K, Eberly J H 1998 Opt. Express 2 368
Google Scholar
[10] Paparelle I, Moro L, Prati E 2020 Phys. Lett. A 384 126266
Google Scholar
[11] Ringot J, Szriftgiser P, Garreau J C 2001 Phys. Rev. A 65 013403
Google Scholar
[12] Thomas J E, Hemmer P R, Ezekiel S, Leiby C C, Picard R H, Willis C R 1982 Phys. Rev. Lett. 48 867
Google Scholar
[13] Xu Z X, Wu Y L, Tian L, Chen L R, Zhang Z Y, Yan Z H, Li S J, Wang H, Xie C D, Peng K C 2013 Phys. Rev. Lett. 111 240503
Google Scholar
[14] Král P, Shapiro M 2001 Phys. Rev. Lett. 87 183002
Google Scholar
[15] Thanopulos I, Král P, Shapiro M 2003 J. Chem. Phys. 119 5105
Google Scholar
[16] Fu Z K, Wang P J, Chai S J, Huang L H, Zhang J 2011 Phys. Rev. A 84 043609
Google Scholar
[17] Lin Y J, Compton R L, Perry A R, Phillips W D, Porto J V, Spielman I B 2009 Phys. Rev. Lett. 102 130401
Google Scholar
[18] Spielman I B 2009 Phys. Rev. A 79 063613
Google Scholar
[19] Lin Y J, Compton R L, Jiménez-García K, Porto J V, Spielman I B 2009 Nature 462 628
Google Scholar
[20] Lin Y J, Jiménez-García K, Spielman I B 2011 Nature 471 83
Google Scholar
[21] Wang P J, Yu Z Q, Fu Z K, Miao J, Huang L H, Chai S J, Zhai H, Zhang J 2012 Phys. Rev. Lett. 109 095301
Google Scholar
[22] Huang L H, Meng Z M, Wang P J, Peng P, Zhang S L, Chen L C, Li D H, Zhou Q, Zhang J 2016 Nat. Phys. 12 540
Google Scholar
[23] Ozawa T, Price H M 2019 Nat. Rev. Phys. 1 349
Google Scholar
[24] Meng Z M, Huang L H, Peng P, Li D H, Chen L C, Xu Y, Zhang C W, Wang P J, Zhang J 2016 Phys. Rev. Lett. 117 235304
Google Scholar
[25] Wu Z, Zhang L, Sun W, Xu X T, Wang B Z, Ji S C, Deng Y J, Chen S, Liu X J, Pan J W 2016 Science 354 83
Google Scholar
[26] Zhang D F, Gao T Y, Zou P, Kong L G, Li R Z, Shen X, Chen X L, Peng S G, Zhan M S, Pu H, Jiang K J 2019 Phys. Rev. Lett. 122 110402
Google Scholar
[27] Zhai H 2012 Int. J. Mod. Phys. B 26 1230001
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 5392
- PDF Downloads: 100
- Cited By: 0
