-
在考虑空气阻力影响, 确定液滴撞击球面速度的基础上, 对较高韦伯数液滴撞击干燥球面动态行为过程进行了实验研究, 分析了球面曲率与韦伯数对液滴撞击行为和铺展因子的影响, 并与前人撞击平面结果进行了对比. 实验表明, 靠近撞击球面时, 液滴降落速度出现明显波动; 球面曲率对液滴撞击后行为影响明显, 曲率较大时, 液滴撞击后铺展液膜会超出球面直径并滑落, 曲率较小时, 液滴撞击后在球面上呈现明显的铺展、回缩、震荡、着附动态变化行为, 此时最大铺展因子受曲率影响小, 随曲率减小, 逐渐趋向于撞击平面时的最大铺展因子; 韦伯数对液膜铺展速率影响较小, 但对液膜回缩时间影响明显, 最大铺展因子随韦伯数增加逐渐增大, 获得的关联式呈指数变化.The phenomenon that droplets impacting on the solid surface is ubiquitous in industrial applications such as spray cooling, spray painting, ink-jet printing, and fuel-air mixing internal combustion engines. The dynamic of droplet impacting on solid surface has been a hot topic in the area of fluid mechanics. Most of the existing experimental studies focused on the droplet impacting on flat or cylinder surface whereas the droplet impacting on a dry sphere surface, especially its effect from the sphere curvature, has been less investigated. Therefore, the dynamic behavior of a droplet impacting normally on a dry sphere is experimentally investigated at the relatively high Reynolds and Weber number in the present work. The impacting velocity of the droplet on the sphere is discussed with consideration of air resistance effect. The influences of spherical curvature and Weber number on the dynamic behavior and spreading factor are analyzed. The experimental results are compared with those of previous impacting flat researches. The results show that the drop velocity fluctuates significantly near the impacting sphere. The influence of the spherical curvature on the dynamic behavior of the droplet impact is obvious. The maximum spreading diameter of the liquid film will exceed that of the sphere with a curvature greater than 0.2 mm–1, and some segments of the liquid film rim even slide down directly. When the spherical curvature is less than 0.167 mm–1, the dynamic behaviors of the impacting droplet will undergo the spread, retraction, oscillation, and stable attachment after impacting. Then the maximum spreading factor of the droplet impacting sphere is little influenced by the curvature, and gradually tends to that of the droplet impacting plane with curvature decreasing. The Weber number has little influence on the spreading velocity of the liquid film, but obvious on the retraction. The maximum spreading factor gradually increases with Weber number increasing. A simple empirical correlation for the maximum spreading factor is obtained. This study conduces significantly to further investigating the dynamic characteristics of droplets impacting on the sphere.
-
Keywords:
- droplet /
- impingement /
- spherical surface /
- hydrodynamics
[1] Hsieh S, Luo S 2016 Int. J. Heat Mass Transfer 92 190
Google Scholar
[2] Zama Y, Odawara Y, Furuhata T 2017 Fuel 203 757
Google Scholar
[3] Lim T, Han S, Chung J, Chung J T, Ko S, Grigoropoulos C P 2009 Int. J. Heat Mass Transfer 52 431
Google Scholar
[4] Gao J, Xu C, Lin S, Yang G, Guo Y 2001 Aiche J. 47 677
Google Scholar
[5] Nayak S V, Joshi S L, Ranade V V 2005 Chem. Eng. Sci. 60 6049
Google Scholar
[6] Rein M 1993 Fluid Dyn. Res. 12 61
Google Scholar
[7] 郭加宏, 戴世强, 代钦 2010 59 2601
Google Scholar
Guo J H, Dai S Q, Dai Q 2010 Acta Phys. Sin. 59 2601
Google Scholar
[8] 黄虎, 洪宁, 梁宏, 施保昌, 柴振华 2016 65 084702
Google Scholar
Huang H, Hong N, Liang H, Shi B C, Chai Z H 2016 Acta Phys. Sin. 65 084702
Google Scholar
[9] Chandra S, Avedisian C T 1991 P Roy Soc. A-Math. Phy. 432 13
Google Scholar
[10] 叶学民, 张湘珊, 李明兰, 李春曦 2018 67 184704
Google Scholar
Ye X M, Zhang X S, Li M L, Li C X 2018 Acta Phys. Sin. 67 184704
Google Scholar
[11] 丁思源, 王瑞祥, 徐荣吉, 张一灏, 蔡骥驰 2016 化工学报 67 2495
Google Scholar
Ding S Y, Wang R X, Xu R J, Zhang Y H, Cai J C 2016 J. Chem. Ind. Eng. 67 2495
Google Scholar
[12] Palacios J, Hernández J, Gómez P, Zanzi C, López J 2013 Exp. Therm. Fluid Sci. 44 571
Google Scholar
[13] 张彬, 韩强, 袁小芳, 李景银 2013 西安交通大学学报 47 23
Google Scholar
Zhang B, Han Q, Yuan X F, Li J Y 2013 J. Xi'an Jiaotong Univ. 47 23
Google Scholar
[14] 姚一娜, 李聪, 陶振翔, 杨锐 2019 清华大学学报(自然科学版) 59 129
Google Scholar
Yao Y N, Li C, Tao Z, Yang R 2019 J. Tsinghua Univ. (Sci. Technol.) 59 129
Google Scholar
[15] Vaikuntanathan V, Kannan R, Sivakumar D 2010 Colloids Surf., A 369 65
Google Scholar
[16] Hu H B, Huang S H, Chen L B 2013 Chin. Phys. B 22 084702
Google Scholar
[17] 冯伟, 郑刚, 聂万胜 2016 推进技术 37 1136
Google Scholar
Feng W, Zheng G, Nie W S 2016 J. Propul. Technol. 37 1136
Google Scholar
[18] 赵宇炜, 杨龙滨, 葛坤, 李彦军 2014 燃烧科学与技术 2014 20
Google Scholar
Zhao Y W, Yang L B, Ge K, Li Y J 2014 J. Combust. Sci. Technol. 2014 20
Google Scholar
[19] Xie C, Zhang J, Bertola V, Wang M 2016 J. Colloid Interface Sci. 463 317
Google Scholar
[20] Khoufech A, Benali M, Saleh K 2015 Powder Technol. 270 599
Google Scholar
[21] Huang Q, Zhang H 2008 Pet. Sci. 5 62
Google Scholar
[22] Tang C, Qin M, Weng X, Zhang X, Zhang P, Li J, Huang Z 2017 Int. J. Multiphase Flow 96 56
Google Scholar
[23] Pasandideh-Fard M, Qiao Y M, Chandra S, Mostaghimi J 1996 Phys. Fluids 8 650
Google Scholar
[24] Khojasteh D, Kazerooni M, Salarian S, Kamali R 2016 J. Ind. Eng. Chem. 42 1
Google Scholar
[25] 刘邱祖, 寇子明, 韩振南, 高贵军 2013 62 234701
Google Scholar
Liu Q Z, Kou Z M, Han Z N, Gao G J 2013 Acta Phys. Sin. 62 234701
Google Scholar
[26] Sun Z H, Han R J 2008 Chin. Phys. B 17 3185
Google Scholar
[27] Khojasteh D, Kazerooni N M, Marengo M 2019 J. Ind. Eng. Chem. 71 50
Google Scholar
[28] 李玉杰, 黄军杰, 肖旭斌 2018 67 184701
Google Scholar
Li Y J, Huang J J, Xiao X B 2018 Acta Phys. Sin. 67 184701
Google Scholar
[29] Liu Y, Andrew M, Li J, Yeomans J M, Wang Z 2015 Nat. Commun. 6 1
Google Scholar
[30] Shamit B, Ilia V R, Cam T 2007 Phys. Fluids 19 032102
Google Scholar
[31] Liang G, Guo Y, Mu X, Shen S 2014 Exp. Therm. Fluid Sci. 55 150
Google Scholar
[32] 梁刚涛, 郭亚丽, 沈胜强 2013 62 184703
Google Scholar
Liang G T, Guo Y L, Shen S Q 2013 Acta Phys. Sin. 62 184703
Google Scholar
[33] Hardalupas Y, Taylor A M K P, Wilkins J H 1999 Int. J. Heat Fluid Fl. 20 477
Google Scholar
[34] Zhu Y, Liu H, Mu K, Gao P, Ding H, Lu X 2017 J. Fluid Mech. 82 4
Google Scholar
[35] Tabakova S, Feuillebois F 2004 J. Colloid Interface Sci. 272 225
Google Scholar
[36] Rioboo R, Marengo M, Tropea C 2002 Exp. Fluids 33 112
Google Scholar
[37] Range K, Feuillebois F 1998 J. Colloid Interface Sci. 203 16
Google Scholar
[38] Huang Y C, Hammitt F G, Yang W J 1973 J. Fluids Eng. 95 276
Google Scholar
[39] Clanet C, Béguin C, Richard D, Quéré D 1999 J. Fluid Mech. 517 199
Google Scholar
-
图 1 液滴撞击球面实验装置系统
Fig. 1. Experimental set up of the droplet impacting on spherical surface.
图 2 液滴速度和直径测量 (a)撞击前; (b) 撞击平面; (c) 撞击球面; (d) 速度分析
Fig. 2. Measurement of droplet diameter and its velocity: (a) Before impacting; (b) impacting plane; (c) impacting spherical surface; (d) velocity analysis.
图 3 液滴下落的速度 (δ = 0.05 mm–1, We = 632.76)
Fig. 3. Velocity of the falling droplet (δ = 0.05 mm–1, We = 632.76).
图 4 不同高度下降落液滴撞击时速度
Fig. 4. Impacting velocity of falling droplets at different heights.
图 5 水滴撞击两种曲率球面的动态行为(We = 632.76, Re = 13906.83) (a) δ = 0.05 mm–1; (b) δ = 0.25 mm–1
Fig. 5. Dynamic behavior of drops impacting on spherical surface of two curvatures (We = 632.76, Re = 13906.83): (a) δ = 0.05 mm–1; (b) δ = 0.25 mm–1.
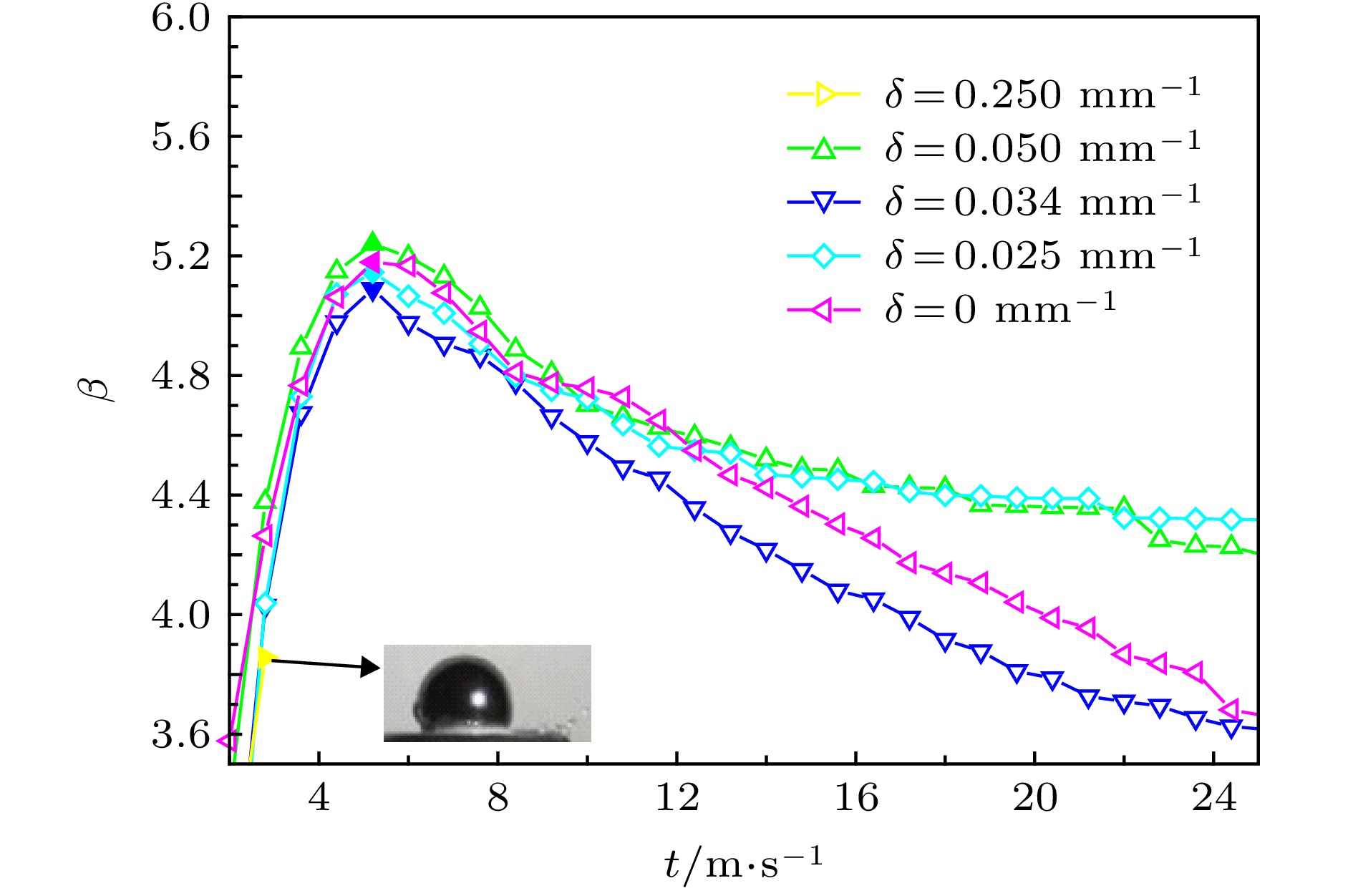
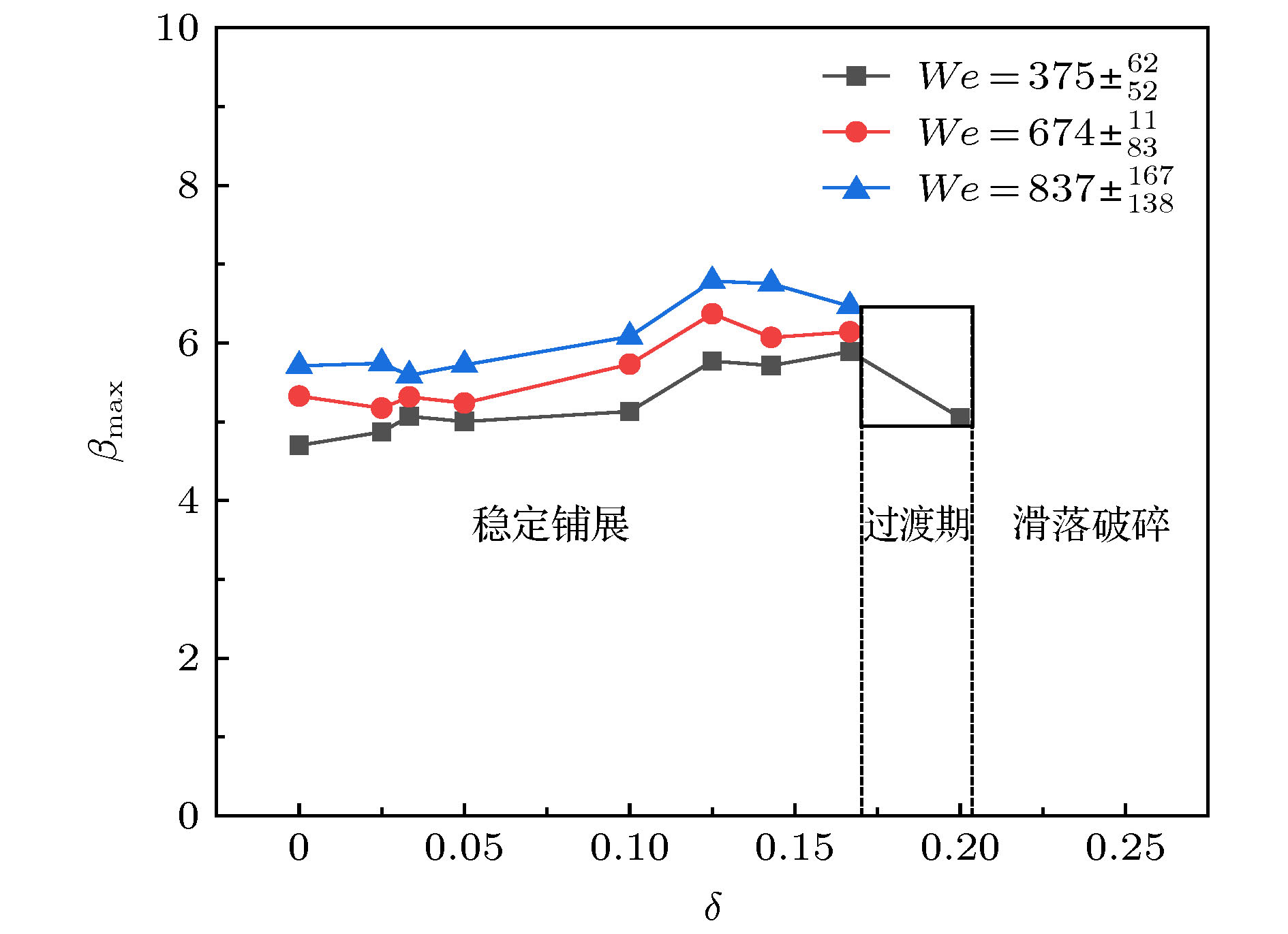
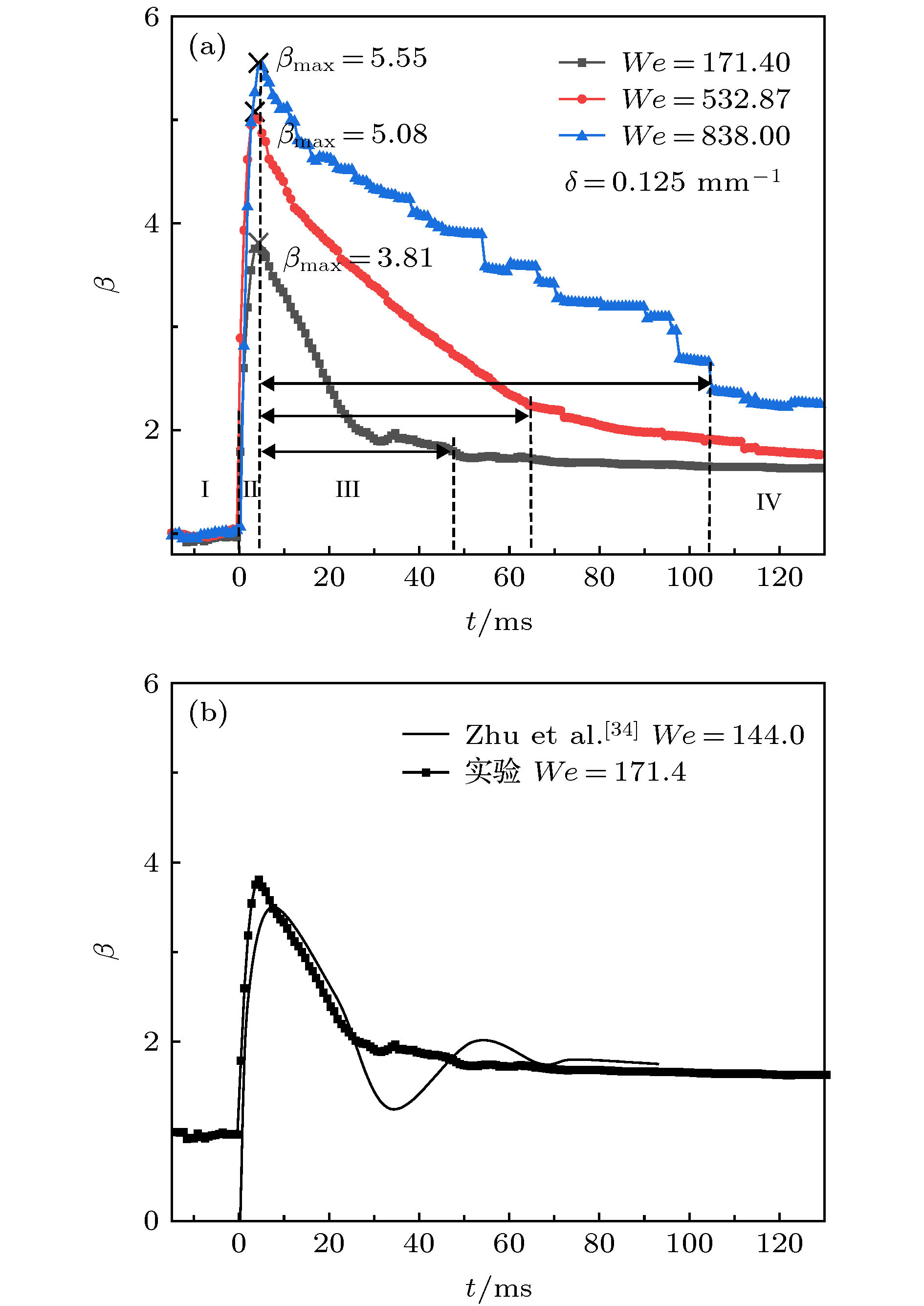
图 6 不同撞击曲率下的动态铺展因子实时分布
$\left( {We = 674 \pm _{83}^{11}, \;Re = 14257 \pm _{1654}^{1025}, \;{V_{{\rm{im}}}} = 3.8{\rm{ m}}/{\rm{s}}} \right)$ Fig. 6. Dynamic spreading factor of droplet impacting on different curvatures
$\left( {We = 674 \pm _{83}^{11},\;Re = 14257 \pm _{1654}^{1025},} \right.$ $\left. {{V_{{\rm{im}}}} = 3.8{\rm{m}}/{\rm{s}}} \right)$ 
图 8 球面曲率对最大铺展因子的影响
Fig. 8. Influence of spherical curvature on the maximum spreading factor.
图 9 不同韦伯数下液滴撞击球面行为的动态过程 (δ = 0.125 mm–1) (a) We = 171.40; (b) We = 532.87; (c) We = 838.00
Fig. 9. Dynamic behavior of droplet impacting on spherical surface for different We (δ = 0.125 mm–1): (a) We = 171.40; (b) We = 532.87; (c) We = 838.00.
图 11 不同曲率下韦伯数对最大铺展因子的影响
Fig. 11. Influence of We on maximum spreading factor for different curvatures.
表 1 撞击壁面结构参数
Table 1. Structure parameters of impacting surface
壁面结构 平面 球形 球形 球形 球形 球形 球形 撞击小球
直径 d/mm∞ 8 16 20 40 60 80 曲率 δ/mm–1 0 0.250 0.125 0.100 0.050 0.034 0.025 
下载: 导出CSV
-
[1] Hsieh S, Luo S 2016 Int. J. Heat Mass Transfer 92 190
Google Scholar
[2] Zama Y, Odawara Y, Furuhata T 2017 Fuel 203 757
Google Scholar
[3] Lim T, Han S, Chung J, Chung J T, Ko S, Grigoropoulos C P 2009 Int. J. Heat Mass Transfer 52 431
Google Scholar
[4] Gao J, Xu C, Lin S, Yang G, Guo Y 2001 Aiche J. 47 677
Google Scholar
[5] Nayak S V, Joshi S L, Ranade V V 2005 Chem. Eng. Sci. 60 6049
Google Scholar
[6] Rein M 1993 Fluid Dyn. Res. 12 61
Google Scholar
[7] 郭加宏, 戴世强, 代钦 2010 59 2601
Google Scholar
Guo J H, Dai S Q, Dai Q 2010 Acta Phys. Sin. 59 2601
Google Scholar
[8] 黄虎, 洪宁, 梁宏, 施保昌, 柴振华 2016 65 084702
Google Scholar
Huang H, Hong N, Liang H, Shi B C, Chai Z H 2016 Acta Phys. Sin. 65 084702
Google Scholar
[9] Chandra S, Avedisian C T 1991 P Roy Soc. A-Math. Phy. 432 13
Google Scholar
[10] 叶学民, 张湘珊, 李明兰, 李春曦 2018 67 184704
Google Scholar
Ye X M, Zhang X S, Li M L, Li C X 2018 Acta Phys. Sin. 67 184704
Google Scholar
[11] 丁思源, 王瑞祥, 徐荣吉, 张一灏, 蔡骥驰 2016 化工学报 67 2495
Google Scholar
Ding S Y, Wang R X, Xu R J, Zhang Y H, Cai J C 2016 J. Chem. Ind. Eng. 67 2495
Google Scholar
[12] Palacios J, Hernández J, Gómez P, Zanzi C, López J 2013 Exp. Therm. Fluid Sci. 44 571
Google Scholar
[13] 张彬, 韩强, 袁小芳, 李景银 2013 西安交通大学学报 47 23
Google Scholar
Zhang B, Han Q, Yuan X F, Li J Y 2013 J. Xi'an Jiaotong Univ. 47 23
Google Scholar
[14] 姚一娜, 李聪, 陶振翔, 杨锐 2019 清华大学学报(自然科学版) 59 129
Google Scholar
Yao Y N, Li C, Tao Z, Yang R 2019 J. Tsinghua Univ. (Sci. Technol.) 59 129
Google Scholar
[15] Vaikuntanathan V, Kannan R, Sivakumar D 2010 Colloids Surf., A 369 65
Google Scholar
[16] Hu H B, Huang S H, Chen L B 2013 Chin. Phys. B 22 084702
Google Scholar
[17] 冯伟, 郑刚, 聂万胜 2016 推进技术 37 1136
Google Scholar
Feng W, Zheng G, Nie W S 2016 J. Propul. Technol. 37 1136
Google Scholar
[18] 赵宇炜, 杨龙滨, 葛坤, 李彦军 2014 燃烧科学与技术 2014 20
Google Scholar
Zhao Y W, Yang L B, Ge K, Li Y J 2014 J. Combust. Sci. Technol. 2014 20
Google Scholar
[19] Xie C, Zhang J, Bertola V, Wang M 2016 J. Colloid Interface Sci. 463 317
Google Scholar
[20] Khoufech A, Benali M, Saleh K 2015 Powder Technol. 270 599
Google Scholar
[21] Huang Q, Zhang H 2008 Pet. Sci. 5 62
Google Scholar
[22] Tang C, Qin M, Weng X, Zhang X, Zhang P, Li J, Huang Z 2017 Int. J. Multiphase Flow 96 56
Google Scholar
[23] Pasandideh-Fard M, Qiao Y M, Chandra S, Mostaghimi J 1996 Phys. Fluids 8 650
Google Scholar
[24] Khojasteh D, Kazerooni M, Salarian S, Kamali R 2016 J. Ind. Eng. Chem. 42 1
Google Scholar
[25] 刘邱祖, 寇子明, 韩振南, 高贵军 2013 62 234701
Google Scholar
Liu Q Z, Kou Z M, Han Z N, Gao G J 2013 Acta Phys. Sin. 62 234701
Google Scholar
[26] Sun Z H, Han R J 2008 Chin. Phys. B 17 3185
Google Scholar
[27] Khojasteh D, Kazerooni N M, Marengo M 2019 J. Ind. Eng. Chem. 71 50
Google Scholar
[28] 李玉杰, 黄军杰, 肖旭斌 2018 67 184701
Google Scholar
Li Y J, Huang J J, Xiao X B 2018 Acta Phys. Sin. 67 184701
Google Scholar
[29] Liu Y, Andrew M, Li J, Yeomans J M, Wang Z 2015 Nat. Commun. 6 1
Google Scholar
[30] Shamit B, Ilia V R, Cam T 2007 Phys. Fluids 19 032102
Google Scholar
[31] Liang G, Guo Y, Mu X, Shen S 2014 Exp. Therm. Fluid Sci. 55 150
Google Scholar
[32] 梁刚涛, 郭亚丽, 沈胜强 2013 62 184703
Google Scholar
Liang G T, Guo Y L, Shen S Q 2013 Acta Phys. Sin. 62 184703
Google Scholar
[33] Hardalupas Y, Taylor A M K P, Wilkins J H 1999 Int. J. Heat Fluid Fl. 20 477
Google Scholar
[34] Zhu Y, Liu H, Mu K, Gao P, Ding H, Lu X 2017 J. Fluid Mech. 82 4
Google Scholar
[35] Tabakova S, Feuillebois F 2004 J. Colloid Interface Sci. 272 225
Google Scholar
[36] Rioboo R, Marengo M, Tropea C 2002 Exp. Fluids 33 112
Google Scholar
[37] Range K, Feuillebois F 1998 J. Colloid Interface Sci. 203 16
Google Scholar
[38] Huang Y C, Hammitt F G, Yang W J 1973 J. Fluids Eng. 95 276
Google Scholar
[39] Clanet C, Béguin C, Richard D, Quéré D 1999 J. Fluid Mech. 517 199
Google Scholar
下载:
计量
- 文章访问数: 8931
- PDF下载量: 181
- 被引次数: 0
